高中数学人教A版必修3课件:3.2古典概型2课时(共43张PPT)
文档属性
| 名称 | 高中数学人教A版必修3课件:3.2古典概型2课时(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
?
?
第一课时
?
分别说出上述两试验的所有可能的试验结果是什么?每个结果之间都有什么关系?
问题1
试验(1)中,结果有两个:“正面朝上”,“反面朝上”,都是随机事件,且不可能同时发生.
?
问题2
什么是基本事件?有什么特点?
在一个试验可能发生的所有结果中,那些不能再分的最简单的随机事件称为基本事件.
(elementary event)
?
?
例1
解
?
问题3
什么是古典概率模型?
?
问题4
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
?
?
?
?
?
?
例2
?
探究1
运用极大似然法的思想,假设他每道题都是随机选择答案的,可以用摸拟的方法估计他答对17道题以上的概率,可以发现这个概率是很小的;如果他掌握了一定知识,绝大多数题他是会做的,那么他答对17道题以上的概率会比较大,所以他应该掌握了一定的知识.
?
探究2
?
?
例3
?
解
?
?
例4
?
例5
随着检测听数的增加,查出不合格产品的概率怎样变化?为什么质检人员一般都采用抽查的方法而不采用逐个检查的方法?
探究3
检测听数 1 2 3 4 5 6
概率 0.6
0.333
0.8
0.933
1
1
不重不漏
本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的适用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利
用公式P(A)=
小 结
课堂练习
?
作业
?
?
第二课时
知识点1
古典概型的判断
基本事件的特点:①基本事件之间互斥;②所有基本
事件的和为必然事件;③所研究的随机事件都能用这
些基本事件 中的的一部分组合而成.
古典概型的特征:试验中所有可能的基本事件的总数
是有限个,每个基本事件的发生是等可能的.
例1
判断下列概率模型是否是古典概型:
①袋中有除颜色外其它均相同的5个白球,3个黑球
和3个红球,每个球有一个区别于其它球的编号,从
中摸出1个球,有多少种不同的摸法?如果把每个球
的编号看做一个基本事件,是否为古典概型?
②将一粒豆子随机洒在一张桌面上,将豆子所落的
位置看做一个基本事件,是否为古典概型?
解
?
②由于豆子落在桌面上的位置有无数个,即有无数
个基本事件,所以豆子所落的位置为基本事件的概
率不是古典概型.
知识点2
古典概型概率的计算
?
例2
?
⑷求摸出的两个球一红一黄的概率.
想一想?
⑴问共有多少个基本事件;
⑵求摸出两个球都是红球的概率;
⑶求摸出的两个球都是黄球的概率;
?
(1,2)(1,3)(1,4)(1,5)(1,6)(1,7)(1,8)
(2,3)(2,4)(2,5)(2,6)(2,7)(2,8)
(3,4)(3,5)(3,6)(3,7)(3,8)
(4,5)(4,6)(4,7)(4,8)
(5,6)(5,7)(5,8)
(6,7)(6,8)
(7,8)
7
6
5
4
3
2
1
?
28
解
?
?
因此
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
?
故
?
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
?
故
则事件C包含的基本事件有15个,
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
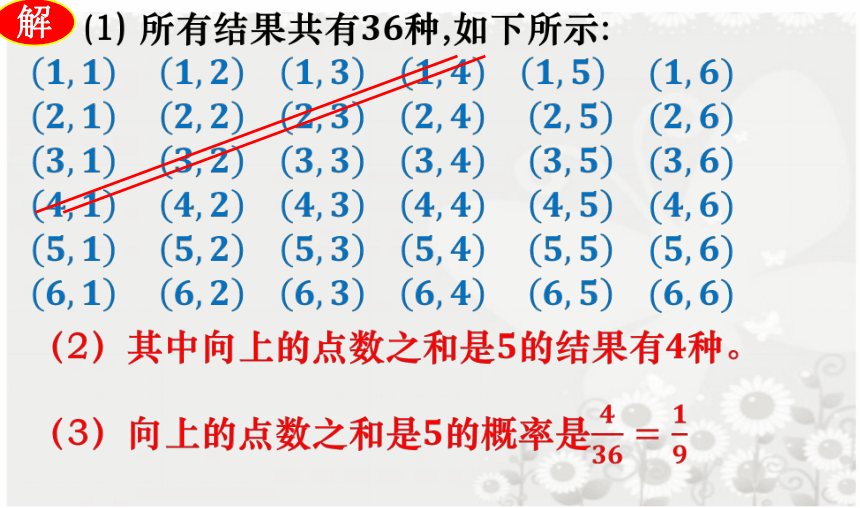
(掷骰子问题):将一个骰子先后抛掷2次,观察向上的点数。
问: (1)共有多少种不同的结果?
(2)两数之和是3的倍数的结果有多少种?
(3)两数之和是3的倍数的概率是多少?
例3
?
解
由表可知,等可能基本事件总数为36种。
6 7 8 9 10 11
第一次抛掷后向上的点数
1 2 3 4 5 6
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
7 8 9 10 11 12
6 7 8 9 10
6
5
4
3
2
1
第二次抛掷后向上的点数
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
(2)记“两次
向上点数之和
是3的倍数”
为事件A,
?
?
?
则事件B的结果有6种,
?
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
?
解
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
根据此表,我们还能得出那些相关结论呢?
?
?
?
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
?
例4
?
身高
体重指标
解
?
?
例5
解
?
?
?
?
例5
解
?
?
?
?
例6
解
?
?
?
?
例7
解
?
?
?
作业
?
?
?
第一课时
?
分别说出上述两试验的所有可能的试验结果是什么?每个结果之间都有什么关系?
问题1
试验(1)中,结果有两个:“正面朝上”,“反面朝上”,都是随机事件,且不可能同时发生.
?
问题2
什么是基本事件?有什么特点?
在一个试验可能发生的所有结果中,那些不能再分的最简单的随机事件称为基本事件.
(elementary event)
?
?
例1
解
?
问题3
什么是古典概率模型?
?
问题4
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
?
?
?
?
?
?
例2
?
探究1
运用极大似然法的思想,假设他每道题都是随机选择答案的,可以用摸拟的方法估计他答对17道题以上的概率,可以发现这个概率是很小的;如果他掌握了一定知识,绝大多数题他是会做的,那么他答对17道题以上的概率会比较大,所以他应该掌握了一定的知识.
?
探究2
?
?
例3
?
解
?
?
例4
?
例5
随着检测听数的增加,查出不合格产品的概率怎样变化?为什么质检人员一般都采用抽查的方法而不采用逐个检查的方法?
探究3
检测听数 1 2 3 4 5 6
概率 0.6
0.333
0.8
0.933
1
1
不重不漏
本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的适用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利
用公式P(A)=
小 结
课堂练习
?
作业
?
?
第二课时
知识点1
古典概型的判断
基本事件的特点:①基本事件之间互斥;②所有基本
事件的和为必然事件;③所研究的随机事件都能用这
些基本事件 中的的一部分组合而成.
古典概型的特征:试验中所有可能的基本事件的总数
是有限个,每个基本事件的发生是等可能的.
例1
判断下列概率模型是否是古典概型:
①袋中有除颜色外其它均相同的5个白球,3个黑球
和3个红球,每个球有一个区别于其它球的编号,从
中摸出1个球,有多少种不同的摸法?如果把每个球
的编号看做一个基本事件,是否为古典概型?
②将一粒豆子随机洒在一张桌面上,将豆子所落的
位置看做一个基本事件,是否为古典概型?
解
?
②由于豆子落在桌面上的位置有无数个,即有无数
个基本事件,所以豆子所落的位置为基本事件的概
率不是古典概型.
知识点2
古典概型概率的计算
?
例2
?
⑷求摸出的两个球一红一黄的概率.
想一想?
⑴问共有多少个基本事件;
⑵求摸出两个球都是红球的概率;
⑶求摸出的两个球都是黄球的概率;
?
(1,2)(1,3)(1,4)(1,5)(1,6)(1,7)(1,8)
(2,3)(2,4)(2,5)(2,6)(2,7)(2,8)
(3,4)(3,5)(3,6)(3,7)(3,8)
(4,5)(4,6)(4,7)(4,8)
(5,6)(5,7)(5,8)
(6,7)(6,8)
(7,8)
7
6
5
4
3
2
1
?
28
解
?
?
因此
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
?
故
?
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
?
故
则事件C包含的基本事件有15个,
(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8)
(2,3), (2,4), (2,5), (2,6), (2,7), (2,8)
(3,4), (3,5), (3,6), (3,7), (3,8)
(4,5), (4,6), (4,7), (4,8)
(5,6), (5,7), (5,8)
(6,7), (6,8)
(7,8)
(掷骰子问题):将一个骰子先后抛掷2次,观察向上的点数。
问: (1)共有多少种不同的结果?
(2)两数之和是3的倍数的结果有多少种?
(3)两数之和是3的倍数的概率是多少?
例3
?
解
由表可知,等可能基本事件总数为36种。
6 7 8 9 10 11
第一次抛掷后向上的点数
1 2 3 4 5 6
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
7 8 9 10 11 12
6 7 8 9 10
6
5
4
3
2
1
第二次抛掷后向上的点数
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
(2)记“两次
向上点数之和
是3的倍数”
为事件A,
?
?
?
则事件B的结果有6种,
?
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
?
解
1 2 3 4 5 6
第一次抛掷后向上的点数
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
6
5
4
3
2
1
第二次抛掷后向上的点数
根据此表,我们还能得出那些相关结论呢?
?
?
?
8 9 10 11 12
6 7 8 9 10 11
6 7 8 9 10
4 5 6 7 8 9
3 4 5 6 7 8
2 3 4 5 6 7
?
例4
?
身高
体重指标
解
?
?
例5
解
?
?
?
?
例5
解
?
?
?
?
例6
解
?
?
?
?
例7
解
?
?
?
作业
?
