二年级上册数学课件-第8单元 1.简单的排列 人教新课标12张PPT
文档属性
| 名称 | 二年级上册数学课件-第8单元 1.简单的排列 人教新课标12张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 22:47:49 | ||
图片预览

文档简介
(共12张PPT)
1.简单的排列
第8章 数学广角——搭配(一)
课程讲授
新知导入
知识应用
随堂练习
新知导入
试一试
剪一些同样大小的长方形纸片,在上面写上“1”“2”“3”,摆一摆,看看他们能组成哪些你认识的数。
1
2
3
可以组成12、32……
课程讲授
用1、2和3组成两位数,每个两位数十位上的数和个位上的数不能一样,能组成几个两位数?
可以组成12、23……
1
2
2
3
做一做:
我有点乱了,有什么好办法吗?
1
2
2
3
做一做:
课程讲授
十位 个位
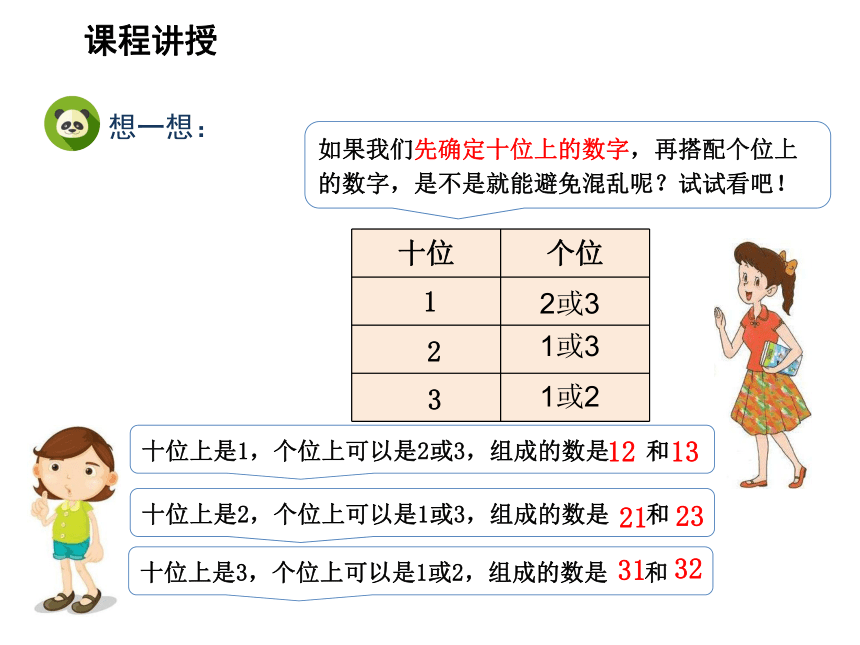
想一想:
如果我们先确定十位上的数字,再搭配个位上的数字,是不是就能避免混乱呢?试试看吧!
1
十位上是1,个位上可以是2或3,组成的数是 和
12
13
十位上是2,个位上可以是1或3,组成的数是 和
2
21
23
十位上是3,个位上可以是1或2,组成的数是 和
3
31
32
2或3
1或3
1或2
课程讲授
十位 个位
想一想:
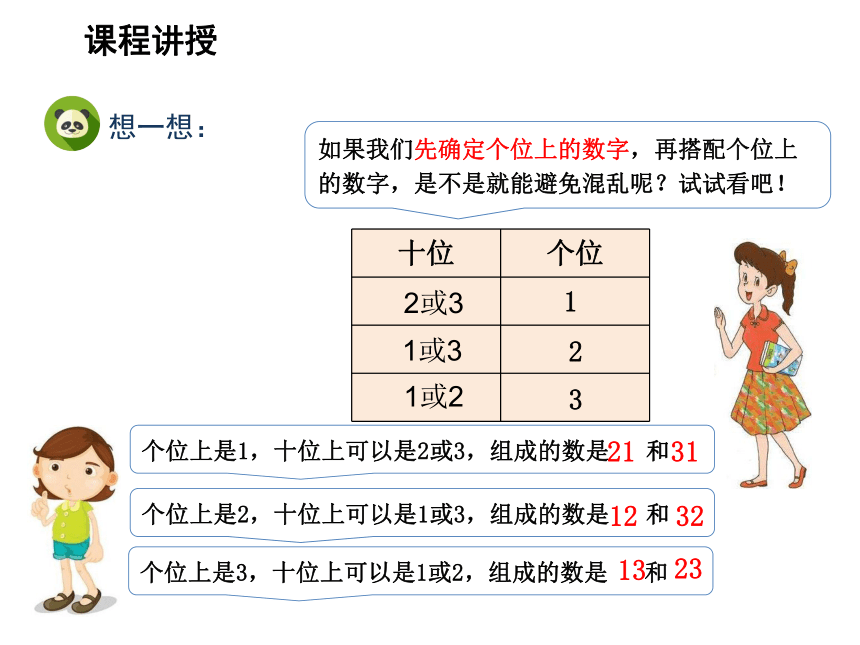
如果我们先确定个位上的数字,再搭配个位上的数字,是不是就能避免混乱呢?试试看吧!
1
个位上是1,十位上可以是2或3,组成的数是 和
21
31
个位上是2,十位上可以是1或3,组成的数是 和
2
12
32
个位上是3,十位上可以是1或2,组成的数是 和
3
13
23
2或3
1或3
1或2
课程讲授
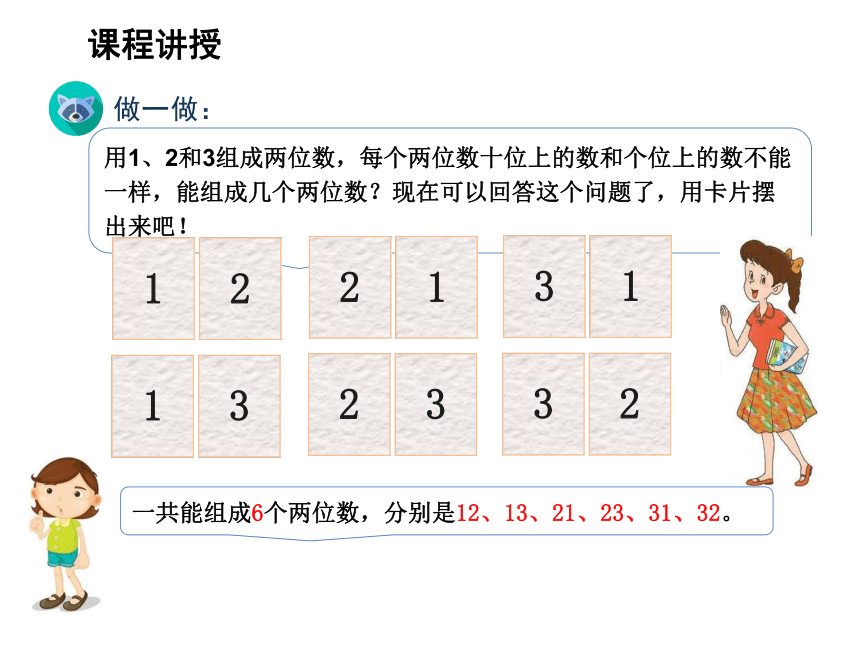
用1、2和3组成两位数,每个两位数十位上的数和个位上的数不能一样,能组成几个两位数?现在可以回答这个问题了,用卡片摆出来吧!
做一做:
1
2
1
3
2
1
2
3
3
1
3
2
一共能组成6个两位数,分别是12、13、21、23、31、32。
知识应用
用 、 和 3种颜色给两个气球涂色,共有多少种方法。
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
一共有6种方法。
随堂练习
1
解决问题
2名同学站成一排合影,有多少种站法?
一共有2种站法。
随堂练习
1
解决问题
如果换成3名同学站成一排合影,有多少种站法?
一共有6种站法。
随堂练习
2
解决问题
北京
伦敦
多伦多
小明有三张明信片,打算挑选2张,送给小丽、小清各1张,一共有多少种送法?
随堂练习
2
解决问题
小清
小丽
小清
小丽
小清
小丽
小清
小丽
小清
小丽
小清
小丽
课堂小结
同学们,通过今天的学习,你有什么收获?
我知道了……
1.简单的排列
第8章 数学广角——搭配(一)
课程讲授
新知导入
知识应用
随堂练习
新知导入
试一试
剪一些同样大小的长方形纸片,在上面写上“1”“2”“3”,摆一摆,看看他们能组成哪些你认识的数。
1
2
3
可以组成12、32……
课程讲授
用1、2和3组成两位数,每个两位数十位上的数和个位上的数不能一样,能组成几个两位数?
可以组成12、23……
1
2
2
3
做一做:
我有点乱了,有什么好办法吗?
1
2
2
3
做一做:
课程讲授
十位 个位
想一想:
如果我们先确定十位上的数字,再搭配个位上的数字,是不是就能避免混乱呢?试试看吧!
1
十位上是1,个位上可以是2或3,组成的数是 和
12
13
十位上是2,个位上可以是1或3,组成的数是 和
2
21
23
十位上是3,个位上可以是1或2,组成的数是 和
3
31
32
2或3
1或3
1或2
课程讲授
十位 个位
想一想:
如果我们先确定个位上的数字,再搭配个位上的数字,是不是就能避免混乱呢?试试看吧!
1
个位上是1,十位上可以是2或3,组成的数是 和
21
31
个位上是2,十位上可以是1或3,组成的数是 和
2
12
32
个位上是3,十位上可以是1或2,组成的数是 和
3
13
23
2或3
1或3
1或2
课程讲授
用1、2和3组成两位数,每个两位数十位上的数和个位上的数不能一样,能组成几个两位数?现在可以回答这个问题了,用卡片摆出来吧!
做一做:
1
2
1
3
2
1
2
3
3
1
3
2
一共能组成6个两位数,分别是12、13、21、23、31、32。
知识应用
用 、 和 3种颜色给两个气球涂色,共有多少种方法。
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
一共有6种方法。
随堂练习
1
解决问题
2名同学站成一排合影,有多少种站法?
一共有2种站法。
随堂练习
1
解决问题
如果换成3名同学站成一排合影,有多少种站法?
一共有6种站法。
随堂练习
2
解决问题
北京
伦敦
多伦多
小明有三张明信片,打算挑选2张,送给小丽、小清各1张,一共有多少种送法?
随堂练习
2
解决问题
小清
小丽
小清
小丽
小清
小丽
小清
小丽
小清
小丽
小清
小丽
课堂小结
同学们,通过今天的学习,你有什么收获?
我知道了……
