2019-2020学年冀教版小学三年级数学(上)期末考试满分模拟卷2(解析版)
文档属性
| 名称 | 2019-2020学年冀教版小学三年级数学(上)期末考试满分模拟卷2(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 00:00:00 | ||
图片预览




文档简介
2019-2020学年冀教版小学三年级数学(上)期末考试满分模拟卷
一.选择题(共8小题)
1.一个亿里有( )个百万.
A.10 B.100 C.1000
2.水果店运进500千克苹果,平均每天卖85千克,卖了4天后,水果店减少了多少千克苹果?正确列式是( )
A.500﹣85×4 B.(500﹣85)×4 C.85×4
3.下面的图形中,有2条对称轴的图形有( )个.
A.1 B.2 C.3 D.4
4.5本《词语手册》的厚度是12厘米,30本同样的《词语手册》的厚度是( )厘米.
A.60 B.66 C.72
5.计算251+76×4时,应( )
A.先算加法 B.先算乘法
C.从左往右按顺序计算
6.下列估计正确的是( )
A.一枚一角硬币重1千克
B.一个鸡蛋重100克
C.1千克棉花比1千克铁轻
D.8千克和800克香蕉同样重
7.甲杯中有水300毫升,乙杯中有水400毫升.第一次先从甲杯中倒10毫升水到乙杯中,第二次再从乙杯中倒20毫升水到甲杯中,第三次再从甲杯中倒30毫升到乙杯中,第四次再从乙杯中倒40毫升到甲杯中,像这样下去,当倒第( )次时甲、乙两杯水一样多.
A.5 B.8 C.9 D.10
8.从长8分米,宽6分米的长方形里剪下一个最大的正方形,这个正方形的周长是( )
A.32分米 B.24分米 C.28分米
二.填空题(共8小题)
9. kg= g
40分= 时
m2= dm2
10.用一根彩带沿一个边长是12厘米的正方形画框的四周绕了一圈还剩2厘米,这根彩带长 分米.
11.在18×3÷6中应该先算 法,在45÷(12﹣3)中应该先算 法,在42÷7+28中应该先算 法.
12.49是7的 倍, 的7倍是63.
8的3倍是 ,15是3的 倍,10个2的和是 .
13.在正方形、长方形、等腰梯形、等边三角形和圆中,请按照对称轴的条数从多到少顺序排列: > > > >
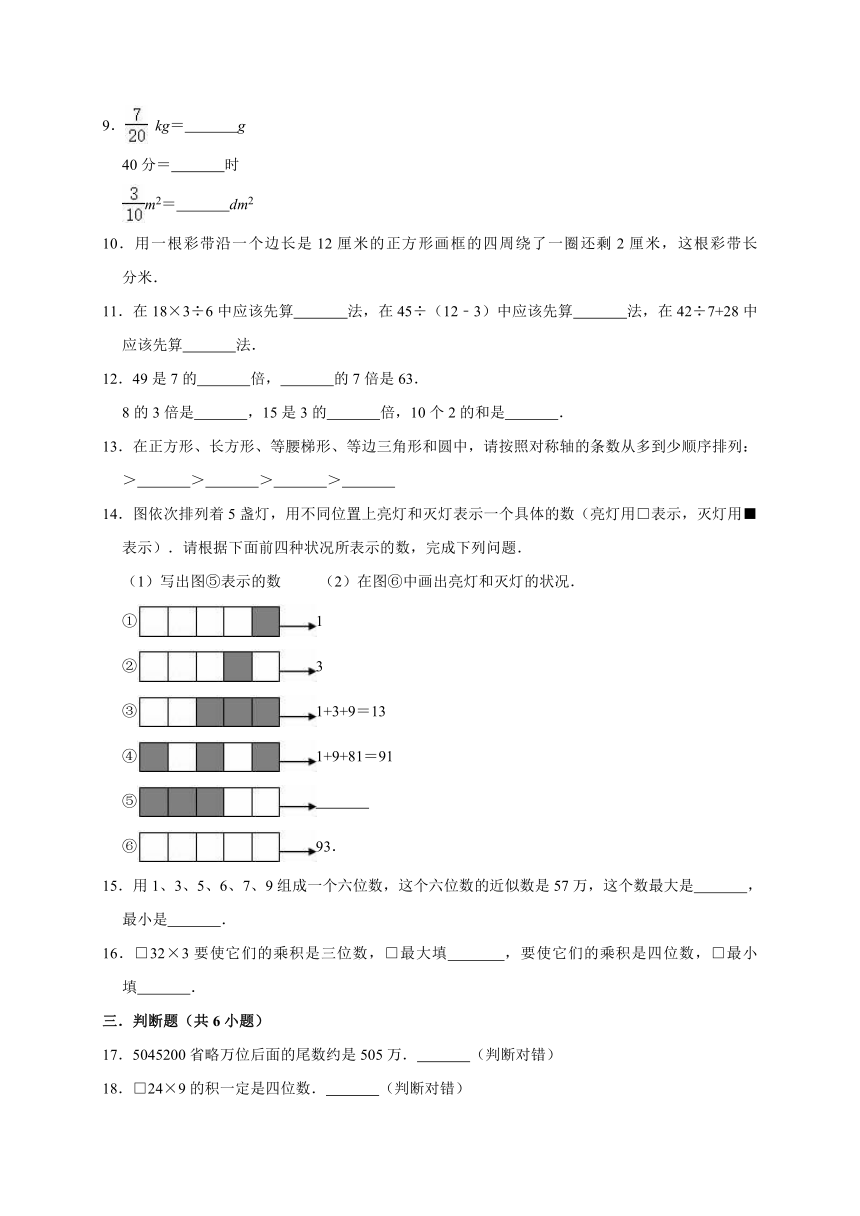
14.图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示).请根据下面前四种状况所表示的数,完成下列问题.
(1)写出图⑤表示的数 (2)在图⑥中画出亮灯和灭灯的状况.
①1
②3
③1+3+9=13
④1+9+81=91
⑤
⑥93.
15.用1、3、5、6、7、9组成一个六位数,这个六位数的近似数是57万,这个数最大是 ,最小是 .
16.□32×3要使它们的乘积是三位数,□最大填 ,要使它们的乘积是四位数,□最小填 .
三.判断题(共6小题)
17.5045200省略万位后面的尾数约是505万. (判断对错)
18.□24×9的积一定是四位数. (判断对错)
19.是轴对称图形. (判断对错)
20.已知一个数是另一个数的几倍,求另一个数,可以用除法做. (判断对错)
21.420÷12×5与420÷60的结果不同. (判断对错)
22.长方形和正方形的周长都是(长+宽)×2. (判断对错)
四.计算题(共1小题)
23.我会脱式计算.
40+60×3
630+280﹣240
五.操作题(共3小题)
24.先填一填再计算下面各图形的周长.
25.把下面每组中的两道算式合并成一道综合算式.
(1)34﹣15=19
19×30=570
列成综合算式
(2)780+120=900
900÷5=180
列成综合算式
(3)450+120=570
800﹣570=230
列成综合算式
(4)60×4=240
240÷8=30
列成综合算式 .
26.连线.
六.应用题(共6小题)
27.丁香小学四年级有260个同学去春游,每40个同学坐一辆车,一共需要几辆车?
28.2010年11月,我国进行了第六次全国人口普查,总人口为1370536875人.如果为希望工程都募捐,只要全国每人拿出1分钱,就能募捐多少元钱?先把这个数改写成以万元为单位的数,再分别精确到十分位和个位.
29.三年二班有50人,每人买一盒彩笔和一袋彩纸,全班一共需要花多少元钱?
30.673加上527的和除以965与905的差,商是多少?
31.一辆自重5000千克的汽车,车上装有3台机床,每台机床重2000千克,要通过一座限重10吨的桥是否安全?
32.把一段铁丝围成长方形,发现长比宽多2厘米,围成正方形时,边长刚好是4厘米,所围成的长方形的长和宽各是多少厘米?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】因为每相邻的两个计数单位之间的进率是10,亿和百万之间隔了一个千万,所以亿和百万之间的进率是100,据此解答即可.
【解答】解:一个亿里有100个百万;
故选:B.
【点评】此题主要考查计数单位之间的进率,要结合数位顺序表完成.
2.【分析】平均每天卖85千克,4天卖了4个85千克,也就是减少了4个85千克,即85×4.
【解答】解:85×4=340(千克)
答:水果店减少了340千克苹果.
故选:C.
【点评】本题关键是明确卖出的质量就是减少的质量,然后再根据乘法的意义进行解答.
3.【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此进行解答即可.
【解答】解:从左数,第一个图形有1条对称轴;
第二个图形不是对称轴图形,所以没有对称轴;
第三个图形有2条对称轴;
第四个图形有1条对称轴,
第五个图形不是对称轴图形,所以没有对称轴;
第六个图形有2条对称轴,
所以,有2条对称轴的图形有2个.
故选:B.
【点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.
4.【分析】因为每本书的厚度是一定的,则书的厚度与书的本数成正比,据此即可列比例求解.
【解答】解:设厚度是x厘米,
则有12:5=x:30
5x=12×30
5x=360
x=72;
答:厚度是72厘米.
故选:C.
【点评】解答此题的关键是明白:如果两个量的商一定,则说这两个量成正比.
5.【分析】251+76×4有乘法和加法,先算乘法,再算加法,由此求解.
【解答】解:251+76×4
=251+304
=555
是先算乘法.
故选:B.
【点评】一个算式里,如果含有两级运算,要先做第二级运算,后做第一级运算.
6.【分析】根据题意,对各个选项依次进行分析,即可得出结论.
【解答】解:根据生活经验、对质量单位和数据大小的认识,可知计量一枚1角硬币重用“克”做单位,约1克;
一个鸡蛋重100克;
1千克棉花和1千克铁一样重;
8千克=8000克;8千克和800克香蕉不一样重;
故选:B.
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择.
7.【分析】根据题意可知,甲杯每经过两次增加10毫升,乙杯每经过两次减少10毫升,要使甲、乙两杯水一样多,即每杯有水(400+300)÷2=350毫升,所以甲杯300毫升增加50毫升,需要5个两次即5×2=10次,解答即可.
【解答】解:(400+300)÷2
=700÷2
=350(毫升)
(350﹣300)÷10×2
=50÷10×2
=5×2
=10(次)
答:当倒第10次时甲、乙两杯水一样多.
故选:D.
【点评】解答此题的关键是弄清每经过两次甲杯增加10毫升,算出要使甲、乙两杯水一样多经过几个两次此题得解.
8.【分析】从长8分米,宽6分米的长方形里剪下一个最大的正方形,这个正方形的边长等于长方形的宽,根据正方形的周长公式:C=4a,把数据代入公式解答.
【解答】解:6×4=24(分米),
答:这个正方形的周长是24分米.
故选:B.
【点评】此题主要考查正方形周长公式的灵活运用,关键是熟记公式.
二.填空题(共8小题)
9.【分析】(1)高级单位千克化低级单位克乘进率1000.
(2)低级单位分化高级单位时除以进率60.
(3)高级单位平方米化低级单位平方分米乘进率100.
【解答】解:(1)kg=350g
(2)40分=时
(3)m2=30dm2.
故答案为:350,,30.
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率;由高级单位化低级单位乘进率,由低级单位化高级单位除以进率.
10.【分析】根据正方形的周长=边长×4求出这个画框的周长,再加上2厘米,就是这根彩带的长度.
【解答】解:12×4+2
=48+2
=50(厘米)
答:这根彩带长 50分米.
故答案为:50.
【点评】此题主要考查了正方形的周长公式的计算应用.
11.【分析】根据整数四则混合运算的运算顺序,可得:在一个没有括号的算式里,既有加、减法,又有乘、除法,要先算乘、除法,后算加、减法,有括号要先算括号里面的.
【解答】解:在18×3÷6中应该先算 乘法,在45÷(12﹣3)中应该先算 减法,在42÷7+28中应该先算 除法.
故答案为:乘,减,除.
【点评】此题主要考查了整数四则混合运算的运算顺序,要熟练掌握,解答此题的关键是要明确.
12.【分析】根据求一个数是另一个数的几倍,用除法计算,用49÷7解答即可;根据已知一个数的几倍是多少,求这个数是多少,用除法计算,用63÷7解答即可;根据求一个数的几倍是多少,用乘法计算,用8×3解答即可;根据求一个数是另一个数的几倍,用除法计算,用15÷3解答即可;根据整数乘法的意义,用2×10解答.
【解答】解:49÷77
63÷79
8×3=24
15÷3=5
2×10=20
答:49是7的 7倍,9的7倍是63.8的3倍是 24,15是3的 5倍,10个2的和是 20.
故答案为:7,9,24,5,20.
【点评】求一个数是另一个数的几倍,用除法计算;已知一个数的几倍是多少求这个数是多少用除法计算;求一个数的几倍是多少和求几个相同加数的和是多少都用乘法计算.
13.【分析】在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴,由此即可判断这个图形的对称轴的条数及位置.
【解答】解:据轴对称图形的特点和定义可知:正方形由四条对称轴,长方形有两条对称轴,等边三角形有三条对称轴,圆形有无数条对称轴,等腰梯形有一条对称轴;
答:这几种图形按对称轴的多少排列是这样的:圆形>正方形>等边三角形>长方形>等腰梯形.
故答案为:圆形、正方形、等边三角形、长方形、等腰梯形.
【点评】此题主要考查如何确定轴对称图形的对称轴条数及位置.
14.【分析】由前4个图可知:当灯灭时(■):从右边向左,第一个灯表示1,第二个灯表示3,第三个灯表示9,第五个灯表示81;1×3=3,3×3=9;后一个数是前一个的3倍,那么第四个灯表示:
9×3=27;
当灯亮时□所表示的数不显示;
⑤中灭的灯是从右边数的第三、四、五这三个就表示9+27+81;
⑥93=81+9+3,应是从右边数的第二、三和五这个三个灯熄灭.
【解答】解:灯熄灭时,从右边向左,第一个灯表示1,第二个灯表示3,第三个灯表示9,第四个灯表示27,第五个灯表示81;
图⑤表示:9+27+81=117;
⑥93=81+9+3,从右边数的第二、三和五这个三个灯熄灭,如图:
.
故答案为:9+27+81=117.
【点评】本题关键是找出各个位置的灯表示的数字,然后再由此进行求解.
15.【分析】由于这个六位数四舍五入到万位是57万,可知前面两位四舍是57,五入是57,四舍的数较大,五入的数较小,
组成最大的六位数确定前面两位是57,千位是3,再把其余数字按照从大到小的顺序排列写成一个六位数;
组成最小的六位数确定前面两位是56,千位是7,再把其余数字字按照从小到大的顺序排列后写成一个六位数.
【解答】解:用1、3、5、6、7、9组成一个六位数,这个六位数的近似数是57万,这个数最大是 573961,最小是 567139.
故答案为:573961,567139.
【点评】给定数字写出这些数字组成的最大的数和最小的数,这是常见的一类题目,最大把这些数按照从大到小排列,最小就按照从小到大排列,注意0不能放在最高位.
16.【分析】用“□32”百位上的数与3相乘得数不能超过10,则□内最大是3,而332×3=996,它们的积是三位数;如果填写4,则432×3=1296,它的积是四位数;由此求解.
【解答】解:当□填写3时:
□32×3
=332×3
=996
当□填写4时:
□32×3
=432×3
=1296
故□32×3要使它们的乘积是三位数,□最大填996,要使它们的乘积是四位数,□最小填1296.
故答案为:996,1296.
【点评】本题运用整数的乘法口诀进行初步的估算,然后再代入式子进行解答计算验证,注意进位的情况.
三.判断题(共6小题)
17.【分析】省略“万”后面的尾数就是四舍五入到万位,把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字,解答判断即可.
【解答】解:5045200≈505万
原题说法是正确的.
故答案为:√.
【点评】本题主要考查整数的求近似数,注意求近似数时要带计数单位.
18.【分析】根据题意,假设□中填入1或9,分别求出各自的乘积,然后再进一步解答.
【解答】解:假设□中填入1或9;
124×9=1116;1116是四位数;
924×9=8316;8316是四位数;
所以,□24×9的积一定是四位数,说法正确;
故答案为:√.
【点评】根据题意,用赋值法能比较容易解决此类问题.
19.【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴,据此即可进行判断.
【解答】解:根据轴对称图形的意义可知:是轴对称图形,说法正确;
故答案为:√.
【点评】解答此题的主要依据是:轴对称图形的意义及特征.
20.【分析】根据题意,要求一个数是另一个数的几倍,也就是求一个数里包含几个另一个数,用除法进行解答.
【解答】解:根据分析可得:
已知一个数是另一个数的几倍,求另一个数,可以用除法做,说法正确;
故答案为:√.
【点评】此题的关键是搞清:求一个数是另一个数的几倍用除法,求一个数的几倍用乘法计算,注意区分.
21.【分析】根据整数四则混合运算的顺序计算出结果再进行比较即可判断.
【解答】解:420÷12×5
=35×5
=175
420÷60=7
175≠7
所以原题说法错误;
故答案为:×.
【点评】此题考查整数四则混合运算顺序,分析数据找到正确的计算方法.
22.【分析】长方形的周长=(长+宽)×2,正方形的周长=边长×4,据此即可判断.
【解答】解:因为长方形的周长=(长+宽)×2,正方形的周长=边长×4,所以原题说法错误.
故答案为:×.
【点评】此题主要考查了长方形、正方形的周长公式的计算应用.
四.计算题(共1小题)
23.【分析】①先算乘法,再算加法;
②先算加法,再算减法.
【解答】解:①40+60×3
=40+180
=220
②630+280﹣240
=910﹣240
=670
【点评】此题考查整数四则混合运算顺序,分析数据找到正确的计算方法.
五.操作题(共3小题)
24.【分析】(1)根据长方形的周长公式:C=(a+b)×2,把数据代入公式解答.
(2)根据正方形的周长公式:C=4a,把数据代入公式解答.
【解答】解:如下图:
(1)(5+3)×2
=8×2
=16(厘米);
答:这个长方形的周长是16厘米.
(2)8×4=32(分米);
答:这个正方形的周长是32分米.
【点评】此题主要考查长方形、正方形周长公式的灵活运用,关键是熟记公式.
25.【分析】(1)先用34减去15求出差,再用求出的差乘上30即可;
(2)先用780加上120求出和,再用求出的和除以5即可;
(3)先用450加上120求出和,再用800减去求出的和即可;
(4)先用60乘上4求出积,再用求出的积除以8即可.
【解答】解:(1)34﹣15=19
19×30=570
列成综合算式:(34﹣15)×30
(2)780+120=900
900÷5=180
列成综合算式:(780+120)÷5
(3)450+120=570
800﹣570=230
列成综合算式:800﹣(450+120)
(4)60×4=240
240÷8=30
列成综合算式:(60×4)÷8.
故答案为:(34﹣15)×30,(780+120)÷5,800﹣(450+120),(60×4)÷8.
【点评】解决这类题目,要分清楚先算什么,再算什么,哪些数是运算出的结果,这些数不要在算式中出现.
26.【分析】(1)把吨、千克、克都化成相同单位的名数,再根据数值的大小进行比较、连线.
(2)把厘米、米、千米都化成相同单位的名数,再根据数值的大小进行比较、连线.
【解答】解:
【点评】本题是考查质量的单位换算、长度的单位换算.单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率.
六.应用题(共6小题)
27.【分析】要求一共需要几辆车,也就是260里面有几个40,即260÷40即可.
【解答】解:260÷40≈7(辆)
答:一共需要7辆车.
【点评】求一个数里面有几个另一个数,用这个数除以另一个数即可.
28.【分析】全国每人拿出1分钱,则共能募捐1370536875分,化成用元做单位的数是13705368.75元,改成用万作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;精确到十分位和个位,就把它们的下一位数进行四舍五入,据此解答.
【解答】解:全国每人拿出1分钱,则共能募捐1370536875分,化成用元做单位的数是13705368.75元;
13705368.75元=1370.536875万元
1370.536875万元≈1370.5万元
1370.536875万元≈1371万元.
【点评】本题主要考查整数的改写和求近似数,注意改写和求近似数时要带计数单位.
29.【分析】彩笔每盒12元,50人需要50个12元,即12×50;彩纸每袋11元,50人需要50个11元,即11×50;然后再相加即可.
【解答】解:12×50+11×50
=600+550
=1150(元)
答:全班一共需要花1150元钱.
【点评】本题关键是根据整数乘法的意义,求出彩笔和彩纸的总价,然后再根据加法的意义进行解答.
30.【分析】先用673加上527求出和,再用965减去905求出差,再用求出的和除以求出的差即可.
【解答】解:(673+527)÷(965﹣905)
=1200÷60
=20
答:商是20.
【点评】这类型的题目要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式求解.
31.【分析】桥的限重是10吨,汽车的质量是5000千克,每台机床的质量是200千克,3台机床的质量就是300×3千克,汽车重加上3台机床的质量如果不超过10吨即可安全过桥,如果大于10吨则不能.
【解答】解:5000+2000×3
=5000+6000
=11000(千克)
11000千克=11吨
11>10
答:要通过一座限重10吨的桥不安全.
【点评】关键是看汽车与货物的质量之和是否大于10吨.吨、千克、克相邻单位间的进率是1000,由高级单位化低级单位乘进率,反之除以进率.
32.【分析】首先根据正方形的周长公式:C=4a,把数据放入公式求出铁丝的长度,然后根据长方形的周长公式,用铁丝的长度除以2减去2,再除以2即可求出宽,进一步求出长.
【解答】解:(4×4÷2﹣2)÷2
=(8﹣2)÷2
=6÷2
=3(厘米)
3+2=5(厘米)
答:所围成的长方形的长是5厘米,宽是3厘米.
【点评】此题主要考查正方形、长方形周长公式的灵活运用,关键是熟记公式.
一.选择题(共8小题)
1.一个亿里有( )个百万.
A.10 B.100 C.1000
2.水果店运进500千克苹果,平均每天卖85千克,卖了4天后,水果店减少了多少千克苹果?正确列式是( )
A.500﹣85×4 B.(500﹣85)×4 C.85×4
3.下面的图形中,有2条对称轴的图形有( )个.
A.1 B.2 C.3 D.4
4.5本《词语手册》的厚度是12厘米,30本同样的《词语手册》的厚度是( )厘米.
A.60 B.66 C.72
5.计算251+76×4时,应( )
A.先算加法 B.先算乘法
C.从左往右按顺序计算
6.下列估计正确的是( )
A.一枚一角硬币重1千克
B.一个鸡蛋重100克
C.1千克棉花比1千克铁轻
D.8千克和800克香蕉同样重
7.甲杯中有水300毫升,乙杯中有水400毫升.第一次先从甲杯中倒10毫升水到乙杯中,第二次再从乙杯中倒20毫升水到甲杯中,第三次再从甲杯中倒30毫升到乙杯中,第四次再从乙杯中倒40毫升到甲杯中,像这样下去,当倒第( )次时甲、乙两杯水一样多.
A.5 B.8 C.9 D.10
8.从长8分米,宽6分米的长方形里剪下一个最大的正方形,这个正方形的周长是( )
A.32分米 B.24分米 C.28分米
二.填空题(共8小题)
9. kg= g
40分= 时
m2= dm2
10.用一根彩带沿一个边长是12厘米的正方形画框的四周绕了一圈还剩2厘米,这根彩带长 分米.
11.在18×3÷6中应该先算 法,在45÷(12﹣3)中应该先算 法,在42÷7+28中应该先算 法.
12.49是7的 倍, 的7倍是63.
8的3倍是 ,15是3的 倍,10个2的和是 .
13.在正方形、长方形、等腰梯形、等边三角形和圆中,请按照对称轴的条数从多到少顺序排列: > > > >
14.图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示).请根据下面前四种状况所表示的数,完成下列问题.
(1)写出图⑤表示的数 (2)在图⑥中画出亮灯和灭灯的状况.
①1
②3
③1+3+9=13
④1+9+81=91
⑤
⑥93.
15.用1、3、5、6、7、9组成一个六位数,这个六位数的近似数是57万,这个数最大是 ,最小是 .
16.□32×3要使它们的乘积是三位数,□最大填 ,要使它们的乘积是四位数,□最小填 .
三.判断题(共6小题)
17.5045200省略万位后面的尾数约是505万. (判断对错)
18.□24×9的积一定是四位数. (判断对错)
19.是轴对称图形. (判断对错)
20.已知一个数是另一个数的几倍,求另一个数,可以用除法做. (判断对错)
21.420÷12×5与420÷60的结果不同. (判断对错)
22.长方形和正方形的周长都是(长+宽)×2. (判断对错)
四.计算题(共1小题)
23.我会脱式计算.
40+60×3
630+280﹣240
五.操作题(共3小题)
24.先填一填再计算下面各图形的周长.
25.把下面每组中的两道算式合并成一道综合算式.
(1)34﹣15=19
19×30=570
列成综合算式
(2)780+120=900
900÷5=180
列成综合算式
(3)450+120=570
800﹣570=230
列成综合算式
(4)60×4=240
240÷8=30
列成综合算式 .
26.连线.
六.应用题(共6小题)
27.丁香小学四年级有260个同学去春游,每40个同学坐一辆车,一共需要几辆车?
28.2010年11月,我国进行了第六次全国人口普查,总人口为1370536875人.如果为希望工程都募捐,只要全国每人拿出1分钱,就能募捐多少元钱?先把这个数改写成以万元为单位的数,再分别精确到十分位和个位.
29.三年二班有50人,每人买一盒彩笔和一袋彩纸,全班一共需要花多少元钱?
30.673加上527的和除以965与905的差,商是多少?
31.一辆自重5000千克的汽车,车上装有3台机床,每台机床重2000千克,要通过一座限重10吨的桥是否安全?
32.把一段铁丝围成长方形,发现长比宽多2厘米,围成正方形时,边长刚好是4厘米,所围成的长方形的长和宽各是多少厘米?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】因为每相邻的两个计数单位之间的进率是10,亿和百万之间隔了一个千万,所以亿和百万之间的进率是100,据此解答即可.
【解答】解:一个亿里有100个百万;
故选:B.
【点评】此题主要考查计数单位之间的进率,要结合数位顺序表完成.
2.【分析】平均每天卖85千克,4天卖了4个85千克,也就是减少了4个85千克,即85×4.
【解答】解:85×4=340(千克)
答:水果店减少了340千克苹果.
故选:C.
【点评】本题关键是明确卖出的质量就是减少的质量,然后再根据乘法的意义进行解答.
3.【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此进行解答即可.
【解答】解:从左数,第一个图形有1条对称轴;
第二个图形不是对称轴图形,所以没有对称轴;
第三个图形有2条对称轴;
第四个图形有1条对称轴,
第五个图形不是对称轴图形,所以没有对称轴;
第六个图形有2条对称轴,
所以,有2条对称轴的图形有2个.
故选:B.
【点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.
4.【分析】因为每本书的厚度是一定的,则书的厚度与书的本数成正比,据此即可列比例求解.
【解答】解:设厚度是x厘米,
则有12:5=x:30
5x=12×30
5x=360
x=72;
答:厚度是72厘米.
故选:C.
【点评】解答此题的关键是明白:如果两个量的商一定,则说这两个量成正比.
5.【分析】251+76×4有乘法和加法,先算乘法,再算加法,由此求解.
【解答】解:251+76×4
=251+304
=555
是先算乘法.
故选:B.
【点评】一个算式里,如果含有两级运算,要先做第二级运算,后做第一级运算.
6.【分析】根据题意,对各个选项依次进行分析,即可得出结论.
【解答】解:根据生活经验、对质量单位和数据大小的认识,可知计量一枚1角硬币重用“克”做单位,约1克;
一个鸡蛋重100克;
1千克棉花和1千克铁一样重;
8千克=8000克;8千克和800克香蕉不一样重;
故选:B.
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择.
7.【分析】根据题意可知,甲杯每经过两次增加10毫升,乙杯每经过两次减少10毫升,要使甲、乙两杯水一样多,即每杯有水(400+300)÷2=350毫升,所以甲杯300毫升增加50毫升,需要5个两次即5×2=10次,解答即可.
【解答】解:(400+300)÷2
=700÷2
=350(毫升)
(350﹣300)÷10×2
=50÷10×2
=5×2
=10(次)
答:当倒第10次时甲、乙两杯水一样多.
故选:D.
【点评】解答此题的关键是弄清每经过两次甲杯增加10毫升,算出要使甲、乙两杯水一样多经过几个两次此题得解.
8.【分析】从长8分米,宽6分米的长方形里剪下一个最大的正方形,这个正方形的边长等于长方形的宽,根据正方形的周长公式:C=4a,把数据代入公式解答.
【解答】解:6×4=24(分米),
答:这个正方形的周长是24分米.
故选:B.
【点评】此题主要考查正方形周长公式的灵活运用,关键是熟记公式.
二.填空题(共8小题)
9.【分析】(1)高级单位千克化低级单位克乘进率1000.
(2)低级单位分化高级单位时除以进率60.
(3)高级单位平方米化低级单位平方分米乘进率100.
【解答】解:(1)kg=350g
(2)40分=时
(3)m2=30dm2.
故答案为:350,,30.
【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率;由高级单位化低级单位乘进率,由低级单位化高级单位除以进率.
10.【分析】根据正方形的周长=边长×4求出这个画框的周长,再加上2厘米,就是这根彩带的长度.
【解答】解:12×4+2
=48+2
=50(厘米)
答:这根彩带长 50分米.
故答案为:50.
【点评】此题主要考查了正方形的周长公式的计算应用.
11.【分析】根据整数四则混合运算的运算顺序,可得:在一个没有括号的算式里,既有加、减法,又有乘、除法,要先算乘、除法,后算加、减法,有括号要先算括号里面的.
【解答】解:在18×3÷6中应该先算 乘法,在45÷(12﹣3)中应该先算 减法,在42÷7+28中应该先算 除法.
故答案为:乘,减,除.
【点评】此题主要考查了整数四则混合运算的运算顺序,要熟练掌握,解答此题的关键是要明确.
12.【分析】根据求一个数是另一个数的几倍,用除法计算,用49÷7解答即可;根据已知一个数的几倍是多少,求这个数是多少,用除法计算,用63÷7解答即可;根据求一个数的几倍是多少,用乘法计算,用8×3解答即可;根据求一个数是另一个数的几倍,用除法计算,用15÷3解答即可;根据整数乘法的意义,用2×10解答.
【解答】解:49÷77
63÷79
8×3=24
15÷3=5
2×10=20
答:49是7的 7倍,9的7倍是63.8的3倍是 24,15是3的 5倍,10个2的和是 20.
故答案为:7,9,24,5,20.
【点评】求一个数是另一个数的几倍,用除法计算;已知一个数的几倍是多少求这个数是多少用除法计算;求一个数的几倍是多少和求几个相同加数的和是多少都用乘法计算.
13.【分析】在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴,由此即可判断这个图形的对称轴的条数及位置.
【解答】解:据轴对称图形的特点和定义可知:正方形由四条对称轴,长方形有两条对称轴,等边三角形有三条对称轴,圆形有无数条对称轴,等腰梯形有一条对称轴;
答:这几种图形按对称轴的多少排列是这样的:圆形>正方形>等边三角形>长方形>等腰梯形.
故答案为:圆形、正方形、等边三角形、长方形、等腰梯形.
【点评】此题主要考查如何确定轴对称图形的对称轴条数及位置.
14.【分析】由前4个图可知:当灯灭时(■):从右边向左,第一个灯表示1,第二个灯表示3,第三个灯表示9,第五个灯表示81;1×3=3,3×3=9;后一个数是前一个的3倍,那么第四个灯表示:
9×3=27;
当灯亮时□所表示的数不显示;
⑤中灭的灯是从右边数的第三、四、五这三个就表示9+27+81;
⑥93=81+9+3,应是从右边数的第二、三和五这个三个灯熄灭.
【解答】解:灯熄灭时,从右边向左,第一个灯表示1,第二个灯表示3,第三个灯表示9,第四个灯表示27,第五个灯表示81;
图⑤表示:9+27+81=117;
⑥93=81+9+3,从右边数的第二、三和五这个三个灯熄灭,如图:
.
故答案为:9+27+81=117.
【点评】本题关键是找出各个位置的灯表示的数字,然后再由此进行求解.
15.【分析】由于这个六位数四舍五入到万位是57万,可知前面两位四舍是57,五入是57,四舍的数较大,五入的数较小,
组成最大的六位数确定前面两位是57,千位是3,再把其余数字按照从大到小的顺序排列写成一个六位数;
组成最小的六位数确定前面两位是56,千位是7,再把其余数字字按照从小到大的顺序排列后写成一个六位数.
【解答】解:用1、3、5、6、7、9组成一个六位数,这个六位数的近似数是57万,这个数最大是 573961,最小是 567139.
故答案为:573961,567139.
【点评】给定数字写出这些数字组成的最大的数和最小的数,这是常见的一类题目,最大把这些数按照从大到小排列,最小就按照从小到大排列,注意0不能放在最高位.
16.【分析】用“□32”百位上的数与3相乘得数不能超过10,则□内最大是3,而332×3=996,它们的积是三位数;如果填写4,则432×3=1296,它的积是四位数;由此求解.
【解答】解:当□填写3时:
□32×3
=332×3
=996
当□填写4时:
□32×3
=432×3
=1296
故□32×3要使它们的乘积是三位数,□最大填996,要使它们的乘积是四位数,□最小填1296.
故答案为:996,1296.
【点评】本题运用整数的乘法口诀进行初步的估算,然后再代入式子进行解答计算验证,注意进位的情况.
三.判断题(共6小题)
17.【分析】省略“万”后面的尾数就是四舍五入到万位,把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字,解答判断即可.
【解答】解:5045200≈505万
原题说法是正确的.
故答案为:√.
【点评】本题主要考查整数的求近似数,注意求近似数时要带计数单位.
18.【分析】根据题意,假设□中填入1或9,分别求出各自的乘积,然后再进一步解答.
【解答】解:假设□中填入1或9;
124×9=1116;1116是四位数;
924×9=8316;8316是四位数;
所以,□24×9的积一定是四位数,说法正确;
故答案为:√.
【点评】根据题意,用赋值法能比较容易解决此类问题.
19.【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴,据此即可进行判断.
【解答】解:根据轴对称图形的意义可知:是轴对称图形,说法正确;
故答案为:√.
【点评】解答此题的主要依据是:轴对称图形的意义及特征.
20.【分析】根据题意,要求一个数是另一个数的几倍,也就是求一个数里包含几个另一个数,用除法进行解答.
【解答】解:根据分析可得:
已知一个数是另一个数的几倍,求另一个数,可以用除法做,说法正确;
故答案为:√.
【点评】此题的关键是搞清:求一个数是另一个数的几倍用除法,求一个数的几倍用乘法计算,注意区分.
21.【分析】根据整数四则混合运算的顺序计算出结果再进行比较即可判断.
【解答】解:420÷12×5
=35×5
=175
420÷60=7
175≠7
所以原题说法错误;
故答案为:×.
【点评】此题考查整数四则混合运算顺序,分析数据找到正确的计算方法.
22.【分析】长方形的周长=(长+宽)×2,正方形的周长=边长×4,据此即可判断.
【解答】解:因为长方形的周长=(长+宽)×2,正方形的周长=边长×4,所以原题说法错误.
故答案为:×.
【点评】此题主要考查了长方形、正方形的周长公式的计算应用.
四.计算题(共1小题)
23.【分析】①先算乘法,再算加法;
②先算加法,再算减法.
【解答】解:①40+60×3
=40+180
=220
②630+280﹣240
=910﹣240
=670
【点评】此题考查整数四则混合运算顺序,分析数据找到正确的计算方法.
五.操作题(共3小题)
24.【分析】(1)根据长方形的周长公式:C=(a+b)×2,把数据代入公式解答.
(2)根据正方形的周长公式:C=4a,把数据代入公式解答.
【解答】解:如下图:
(1)(5+3)×2
=8×2
=16(厘米);
答:这个长方形的周长是16厘米.
(2)8×4=32(分米);
答:这个正方形的周长是32分米.
【点评】此题主要考查长方形、正方形周长公式的灵活运用,关键是熟记公式.
25.【分析】(1)先用34减去15求出差,再用求出的差乘上30即可;
(2)先用780加上120求出和,再用求出的和除以5即可;
(3)先用450加上120求出和,再用800减去求出的和即可;
(4)先用60乘上4求出积,再用求出的积除以8即可.
【解答】解:(1)34﹣15=19
19×30=570
列成综合算式:(34﹣15)×30
(2)780+120=900
900÷5=180
列成综合算式:(780+120)÷5
(3)450+120=570
800﹣570=230
列成综合算式:800﹣(450+120)
(4)60×4=240
240÷8=30
列成综合算式:(60×4)÷8.
故答案为:(34﹣15)×30,(780+120)÷5,800﹣(450+120),(60×4)÷8.
【点评】解决这类题目,要分清楚先算什么,再算什么,哪些数是运算出的结果,这些数不要在算式中出现.
26.【分析】(1)把吨、千克、克都化成相同单位的名数,再根据数值的大小进行比较、连线.
(2)把厘米、米、千米都化成相同单位的名数,再根据数值的大小进行比较、连线.
【解答】解:
【点评】本题是考查质量的单位换算、长度的单位换算.单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率.
六.应用题(共6小题)
27.【分析】要求一共需要几辆车,也就是260里面有几个40,即260÷40即可.
【解答】解:260÷40≈7(辆)
答:一共需要7辆车.
【点评】求一个数里面有几个另一个数,用这个数除以另一个数即可.
28.【分析】全国每人拿出1分钱,则共能募捐1370536875分,化成用元做单位的数是13705368.75元,改成用万作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;精确到十分位和个位,就把它们的下一位数进行四舍五入,据此解答.
【解答】解:全国每人拿出1分钱,则共能募捐1370536875分,化成用元做单位的数是13705368.75元;
13705368.75元=1370.536875万元
1370.536875万元≈1370.5万元
1370.536875万元≈1371万元.
【点评】本题主要考查整数的改写和求近似数,注意改写和求近似数时要带计数单位.
29.【分析】彩笔每盒12元,50人需要50个12元,即12×50;彩纸每袋11元,50人需要50个11元,即11×50;然后再相加即可.
【解答】解:12×50+11×50
=600+550
=1150(元)
答:全班一共需要花1150元钱.
【点评】本题关键是根据整数乘法的意义,求出彩笔和彩纸的总价,然后再根据加法的意义进行解答.
30.【分析】先用673加上527求出和,再用965减去905求出差,再用求出的和除以求出的差即可.
【解答】解:(673+527)÷(965﹣905)
=1200÷60
=20
答:商是20.
【点评】这类型的题目要分清楚数量之间的关系,先求什么再求什么,找清列式的顺序,列出算式求解.
31.【分析】桥的限重是10吨,汽车的质量是5000千克,每台机床的质量是200千克,3台机床的质量就是300×3千克,汽车重加上3台机床的质量如果不超过10吨即可安全过桥,如果大于10吨则不能.
【解答】解:5000+2000×3
=5000+6000
=11000(千克)
11000千克=11吨
11>10
答:要通过一座限重10吨的桥不安全.
【点评】关键是看汽车与货物的质量之和是否大于10吨.吨、千克、克相邻单位间的进率是1000,由高级单位化低级单位乘进率,反之除以进率.
32.【分析】首先根据正方形的周长公式:C=4a,把数据放入公式求出铁丝的长度,然后根据长方形的周长公式,用铁丝的长度除以2减去2,再除以2即可求出宽,进一步求出长.
【解答】解:(4×4÷2﹣2)÷2
=(8﹣2)÷2
=6÷2
=3(厘米)
3+2=5(厘米)
答:所围成的长方形的长是5厘米,宽是3厘米.
【点评】此题主要考查正方形、长方形周长公式的灵活运用,关键是熟记公式.
同课章节目录
