六年级下册数学课件-第三单元 1.圆柱 第7课时 圆柱的体积(3)人教版(共22张PPT)
文档属性
| 名称 | 六年级下册数学课件-第三单元 1.圆柱 第7课时 圆柱的体积(3)人教版(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 405.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 10:53:47 | ||
图片预览





文档简介
(共22张PPT)
人教版数学六年级下册 第三单元
圆柱的体积(3) (教材P27例7)
复习导入
一、判断
1、圆柱是以长方形的一边为轴旋转而得到的。( )
它的高就是旋转一边的边长。( )
它的底面周长就是这个长方形的另一边为半径计算出来的圆的周长。( )
2、圆柱也可以由长方形卷曲而得到。( )
3、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,它们的数值是相等的。( )
4、圆柱的底面可以是不完全相等的两个圆。( )
5、如果圆柱的高和它的底面周长相等,它的侧面沿着高的方向展开,一定是一个正方形。( )
6、一个圆柱的侧面展开是一个正方形,它的高是底面直径的π倍。( )
√
√
√
√
√
×
√
√
7、圆柱的体积和容积并不是同一概念,它的体积是整个圆柱占空间的体积,而它的容积则是圆柱内部空间所占的体积。( )
√
复习导入
二、填空
1、圆的周长计算公式是( )
2、圆的面积计算公式是( )
3、长方体表面积计算公式是( )
4、正方体表面积计算公式是( )
5、圆柱表面积计算公式是( )
6、长方体体积计算公式是( )
8、圆柱体积计算公式是( )
C=πd 或者C =2πr
S=π
S=2 (ab+ac+bc)
S=6
S表= S侧+ 2S圆
S表= 2πr h+ 2 π
V =abc
V =Sh
7、正方体体积计算公式是( )
V=
V=
V=
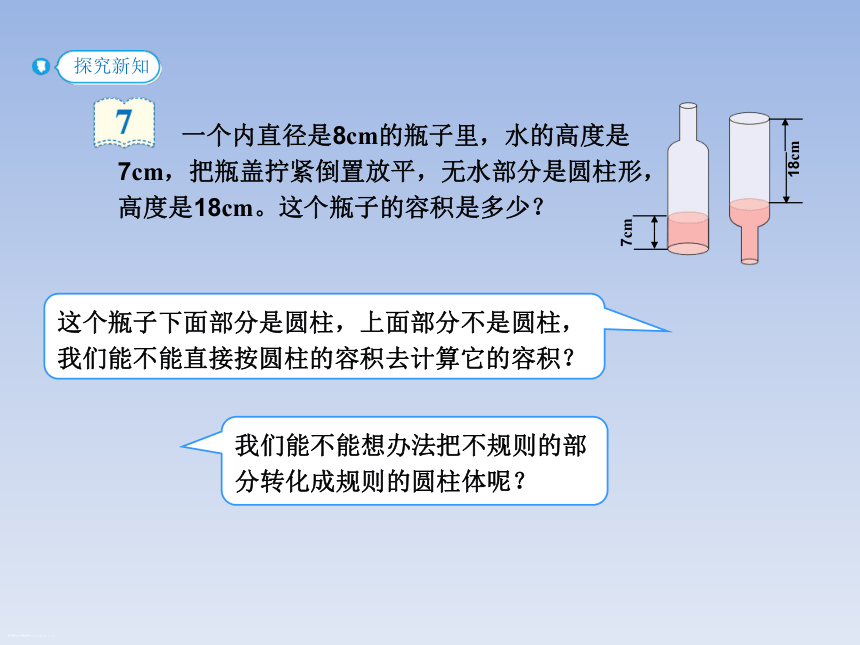
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
这个瓶子下面部分是圆柱,上面部分不是圆柱,我们能不能直接按圆柱的容积去计算它的容积?
绿色圃中小学教育网http://www.Lspjy.com
探究新知
我们能不能想办法把不规则的部分转化成规则的圆柱体呢?
绿色圃中小学教育网http://www.Lspjy.com
探究新知
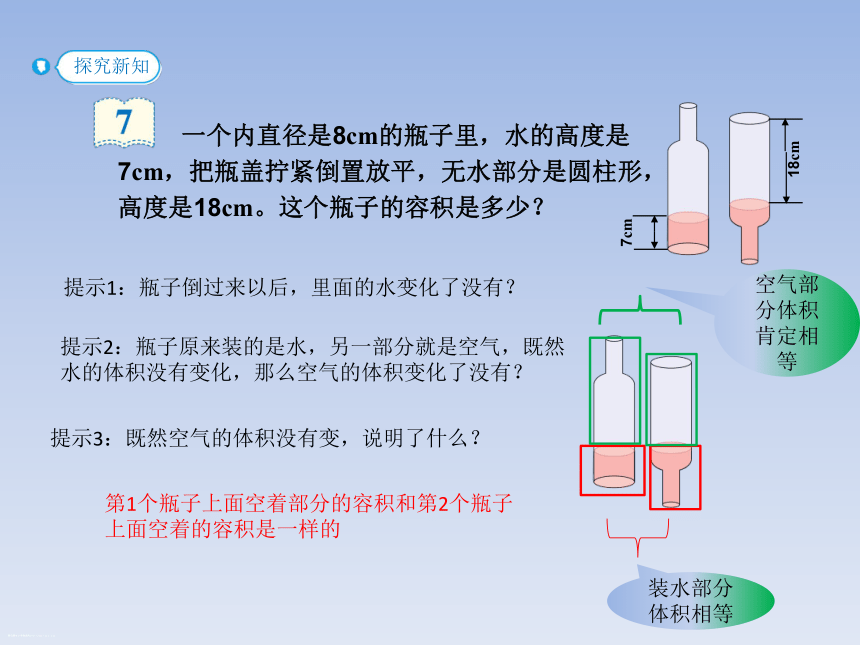
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
提示1:瓶子倒过来以后,里面的水变化了没有?
装水部分体积相等
提示2:瓶子原来装的是水,另一部分就是空气,既然水的体积没有变化,那么空气的体积变化了没有?
空气部分体积肯定相等
提示3:既然空气的体积没有变,说明了什么?
第1个瓶子上面空着部分的容积和第2个瓶子上面空着的容积是一样的
绿色圃中小学教育网http://www.Lspjy.com
探究新知
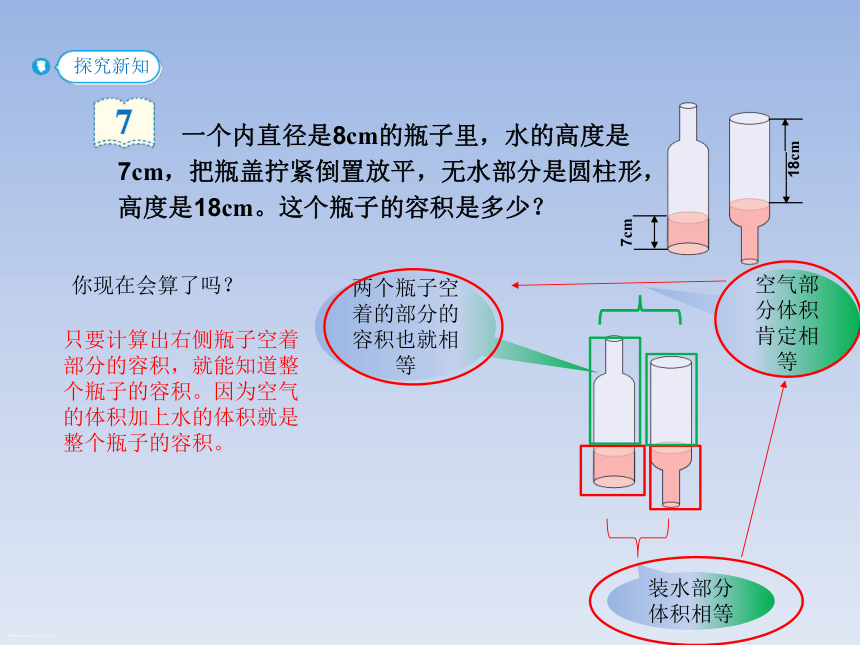
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
装水部分体积相等
空气部分体积肯定相等
两个瓶子空着的部分的容积也就相等
你现在会算了吗?
只要计算出右侧瓶子空着部分的容积,就能知道整个瓶子的容积。因为空气的体积加上水的体积就是整个瓶子的容积。
探究新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
V水=πh=3.14××7
=3.14××7
=351.68()
水的体积:
空气的体积:
V空气=πh=3.14××18
=3.14××18
=9)
瓶子的容积=水的体积+空气的体积=351.68+904.32=1256
答:这个瓶子的容积是1256
探究新知
我们刚才通过转化,把不规则部分转化成了规则的圆柱,通过求圆柱的容积,算出了不规则部分的容积,这就是转化思想,请同学们回忆一下,我们以前用过哪些转化思想?
把平行四边形转化成长方形,通过计算长方形面积来计算平行四边形面积;
把三角形转化成平行四边形,通过计算出平行四边形面积再除以2 算出了三角形的面积;
把圆的面积转化成长方形,通过计算长方形面积,算出了圆的面积;
把圆柱转化成长方体,通过计算长方体体积的方式,计算出了圆柱的体积……
我们以后遇到一些不能直接解决的问题时,要尝试用转化方法去解决。
答:小明喝了282.6mL的水。
3.14×(6÷2)×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
2
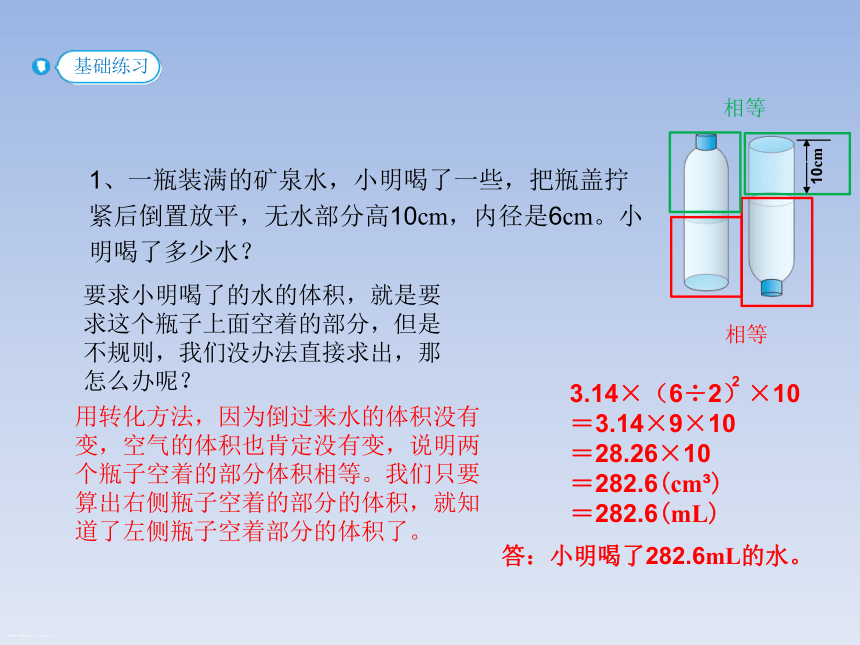
1、一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
绿色圃中小学教育网http://www.Lspjy.com
基础练习
要求小明喝了的水的体积,就是要求这个瓶子上面空着的部分,但是不规则,我们没办法直接求出,那怎么办呢?
用转化方法,因为倒过来水的体积没有变,空气的体积也肯定没有变,说明两个瓶子空着的部分体积相等。我们只要算出右侧瓶子空着的部分的体积,就知道了左侧瓶子空着部分的体积了。
相等
相等
答:现在用了34.215立方米的土石。
35-3.14×(2÷2)×0.25
=35-3.14×1×0.25
=35-0.785
=34.215(m )
2
基础练习
2. 学校要在教学区和操场之间修一道围墙,原计划用土石35m 。
后来多开了一个直径为2米,厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
提示1:现在用的土石比原计划用的土石是多了还是少了?因为什么才导致这样的结果?
少了,因为月亮门的部分不需要用土石。
提示2:少用了的土石的体积和月亮门的体积有什么关系?
少用了的土石的体积就是月亮门的体积。
月亮门的体积你会算吗?
1. 两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
81 ÷4.5=18()
答:它的体积是54dm 。
要求第2个圆柱的体积,必须要知道什么?
拓展练习
它的底面积我们知道吗?能不能算出来?
通过第1个圆柱的体积和高,算出第1个圆柱的底面积:
第1个圆柱的的底面积和第2个圆柱的底面积相等,算出第2个圆柱的体积:
18×3=53()
综合算式: 81 ÷4.5×3= 53()
2. 一个圆柱形玻璃容器的底面直径是10cm,把一块完
全浸泡在这个容器的水中的铁块取出后,水面下降
2cm。这块铁块的体积是多少?
V=π3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
水面因为什么面下降,说明了什么?
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
因为取出了铁块而下降,下降部分水的体积就是铁块的积体。
请你想一想,以长为轴旋转,得到的圆柱是什么样子的?
3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
答:以长为轴旋转一周,得到的圆柱的体积是6280cm 。
3. 右面这个长方形的长是20cm,宽是10cm。
分别以长和宽为轴旋转一周,得到两个圆柱。它们的体积各是多少?
20cm
10cm
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
请你想一想,以宽为轴旋转,得到的圆柱又是什么样子的?
3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
答:以宽为轴旋转一周,得到的圆柱的体积是12560cm 。
3. 右面这个长方形的长是20cm,宽是10cm。
分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试,并算一下卷成的圆柱的体积。
拓展练习
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
答:图4圆柱的体积最小,图1圆柱的体积最大。
18
12
9
6
2
3
4
6
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
半径:18÷π÷2=(dm)
图1
体积:π××2=(dm )
图2
半径:12÷π÷2=(dm)
体积: π ××3=(dm )
半径:9÷ π ÷2=(dm)
图3
体积: π ××4=(dm )
半径:6÷ π ÷2=(dm)
图4
体积: π ××6=(dm )
( )
( )
( )
( )
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
拓展练习
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。长和宽差距越大,卷成的圆柱的体积越大。
以长边为周长,长边越长体积越大
以长为长,越长越大
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
上面4个图形当以宽为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试,并算一算卷成的圆柱体积。
拓展练习
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
答:图1圆柱的体积最小,图4圆柱的体积最大。
绿色圃中小学教育网http://www.Lspjy.com
半径:2÷π÷2=(dm)
图1
体积:π××18=(dm )
图2
半径:3÷π÷2=(dm)
体积: π ×(×12=(dm )
半径:4÷ π ÷2=(dm)
图3
体积: π ××9=(dm )
半径:6÷ π ÷2=(dm)
图4
体积: π ××6=(dm )
拓展练习
( )
( )
( )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
我发现,上面4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。长和宽差距越大时,卷成的圆柱的体积越小。
以短为长,越短越小
以短边为周长,短边越短体积越小
拓展练习
拓展练习
图1
体积:π××2=(dm )
图2
体积: π ××3=(dm )
图3
体积: π ××4=(dm )
图4
体积: π ××6=(dm )
体积:π××18=(dm )
体积: π ×(×12=(dm )
体积: π ××9=(dm )
体积: π ××6=(dm )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
以长边为周长
以短边为周长
( )
( )
( )
( )
( )
( )
( )
拓展练习
图1
体积:π××2=(dm )
体积:π××18=(dm )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
以长边为周长
以短边为周长
同一个长方形,以长作为底面周长时卷成的圆柱体积大,以宽为底面周长时,卷成的圆柱的体积小
( )
( )
人教版数学六年级下册 第三单元
圆柱的体积(3) (教材P27例7)
复习导入
一、判断
1、圆柱是以长方形的一边为轴旋转而得到的。( )
它的高就是旋转一边的边长。( )
它的底面周长就是这个长方形的另一边为半径计算出来的圆的周长。( )
2、圆柱也可以由长方形卷曲而得到。( )
3、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,它们的数值是相等的。( )
4、圆柱的底面可以是不完全相等的两个圆。( )
5、如果圆柱的高和它的底面周长相等,它的侧面沿着高的方向展开,一定是一个正方形。( )
6、一个圆柱的侧面展开是一个正方形,它的高是底面直径的π倍。( )
√
√
√
√
√
×
√
√
7、圆柱的体积和容积并不是同一概念,它的体积是整个圆柱占空间的体积,而它的容积则是圆柱内部空间所占的体积。( )
√
复习导入
二、填空
1、圆的周长计算公式是( )
2、圆的面积计算公式是( )
3、长方体表面积计算公式是( )
4、正方体表面积计算公式是( )
5、圆柱表面积计算公式是( )
6、长方体体积计算公式是( )
8、圆柱体积计算公式是( )
C=πd 或者C =2πr
S=π
S=2 (ab+ac+bc)
S=6
S表= S侧+ 2S圆
S表= 2πr h+ 2 π
V =abc
V =Sh
7、正方体体积计算公式是( )
V=
V=
V=
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
这个瓶子下面部分是圆柱,上面部分不是圆柱,我们能不能直接按圆柱的容积去计算它的容积?
绿色圃中小学教育网http://www.Lspjy.com
探究新知
我们能不能想办法把不规则的部分转化成规则的圆柱体呢?
绿色圃中小学教育网http://www.Lspjy.com
探究新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
提示1:瓶子倒过来以后,里面的水变化了没有?
装水部分体积相等
提示2:瓶子原来装的是水,另一部分就是空气,既然水的体积没有变化,那么空气的体积变化了没有?
空气部分体积肯定相等
提示3:既然空气的体积没有变,说明了什么?
第1个瓶子上面空着部分的容积和第2个瓶子上面空着的容积是一样的
绿色圃中小学教育网http://www.Lspjy.com
探究新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
装水部分体积相等
空气部分体积肯定相等
两个瓶子空着的部分的容积也就相等
你现在会算了吗?
只要计算出右侧瓶子空着部分的容积,就能知道整个瓶子的容积。因为空气的体积加上水的体积就是整个瓶子的容积。
探究新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
V水=πh=3.14××7
=3.14××7
=351.68()
水的体积:
空气的体积:
V空气=πh=3.14××18
=3.14××18
=9)
瓶子的容积=水的体积+空气的体积=351.68+904.32=1256
答:这个瓶子的容积是1256
探究新知
我们刚才通过转化,把不规则部分转化成了规则的圆柱,通过求圆柱的容积,算出了不规则部分的容积,这就是转化思想,请同学们回忆一下,我们以前用过哪些转化思想?
把平行四边形转化成长方形,通过计算长方形面积来计算平行四边形面积;
把三角形转化成平行四边形,通过计算出平行四边形面积再除以2 算出了三角形的面积;
把圆的面积转化成长方形,通过计算长方形面积,算出了圆的面积;
把圆柱转化成长方体,通过计算长方体体积的方式,计算出了圆柱的体积……
我们以后遇到一些不能直接解决的问题时,要尝试用转化方法去解决。
答:小明喝了282.6mL的水。
3.14×(6÷2)×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
2
1、一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
绿色圃中小学教育网http://www.Lspjy.com
基础练习
要求小明喝了的水的体积,就是要求这个瓶子上面空着的部分,但是不规则,我们没办法直接求出,那怎么办呢?
用转化方法,因为倒过来水的体积没有变,空气的体积也肯定没有变,说明两个瓶子空着的部分体积相等。我们只要算出右侧瓶子空着的部分的体积,就知道了左侧瓶子空着部分的体积了。
相等
相等
答:现在用了34.215立方米的土石。
35-3.14×(2÷2)×0.25
=35-3.14×1×0.25
=35-0.785
=34.215(m )
2
基础练习
2. 学校要在教学区和操场之间修一道围墙,原计划用土石35m 。
后来多开了一个直径为2米,厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
提示1:现在用的土石比原计划用的土石是多了还是少了?因为什么才导致这样的结果?
少了,因为月亮门的部分不需要用土石。
提示2:少用了的土石的体积和月亮门的体积有什么关系?
少用了的土石的体积就是月亮门的体积。
月亮门的体积你会算吗?
1. 两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
81 ÷4.5=18()
答:它的体积是54dm 。
要求第2个圆柱的体积,必须要知道什么?
拓展练习
它的底面积我们知道吗?能不能算出来?
通过第1个圆柱的体积和高,算出第1个圆柱的底面积:
第1个圆柱的的底面积和第2个圆柱的底面积相等,算出第2个圆柱的体积:
18×3=53()
综合算式: 81 ÷4.5×3= 53()
2. 一个圆柱形玻璃容器的底面直径是10cm,把一块完
全浸泡在这个容器的水中的铁块取出后,水面下降
2cm。这块铁块的体积是多少?
V=π3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
水面因为什么面下降,说明了什么?
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
因为取出了铁块而下降,下降部分水的体积就是铁块的积体。
请你想一想,以长为轴旋转,得到的圆柱是什么样子的?
3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
答:以长为轴旋转一周,得到的圆柱的体积是6280cm 。
3. 右面这个长方形的长是20cm,宽是10cm。
分别以长和宽为轴旋转一周,得到两个圆柱。它们的体积各是多少?
20cm
10cm
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
请你想一想,以宽为轴旋转,得到的圆柱又是什么样子的?
3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
答:以宽为轴旋转一周,得到的圆柱的体积是12560cm 。
3. 右面这个长方形的长是20cm,宽是10cm。
分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试,并算一下卷成的圆柱的体积。
拓展练习
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
答:图4圆柱的体积最小,图1圆柱的体积最大。
18
12
9
6
2
3
4
6
绿色圃中小学教育网http://www.Lspjy.com
拓展练习
半径:18÷π÷2=(dm)
图1
体积:π××2=(dm )
图2
半径:12÷π÷2=(dm)
体积: π ××3=(dm )
半径:9÷ π ÷2=(dm)
图3
体积: π ××4=(dm )
半径:6÷ π ÷2=(dm)
图4
体积: π ××6=(dm )
( )
( )
( )
( )
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
拓展练习
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。长和宽差距越大,卷成的圆柱的体积越大。
以长边为周长,长边越长体积越大
以长为长,越长越大
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
上面4个图形当以宽为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试,并算一算卷成的圆柱体积。
拓展练习
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
答:图1圆柱的体积最小,图4圆柱的体积最大。
绿色圃中小学教育网http://www.Lspjy.com
半径:2÷π÷2=(dm)
图1
体积:π××18=(dm )
图2
半径:3÷π÷2=(dm)
体积: π ×(×12=(dm )
半径:4÷ π ÷2=(dm)
图3
体积: π ××9=(dm )
半径:6÷ π ÷2=(dm)
图4
体积: π ××6=(dm )
拓展练习
( )
( )
( )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
我发现,上面4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。长和宽差距越大时,卷成的圆柱的体积越小。
以短为长,越短越小
以短边为周长,短边越短体积越小
拓展练习
拓展练习
图1
体积:π××2=(dm )
图2
体积: π ××3=(dm )
图3
体积: π ××4=(dm )
图4
体积: π ××6=(dm )
体积:π××18=(dm )
体积: π ×(×12=(dm )
体积: π ××9=(dm )
体积: π ××6=(dm )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
以长边为周长
以短边为周长
( )
( )
( )
( )
( )
( )
( )
拓展练习
图1
体积:π××2=(dm )
体积:π××18=(dm )
图1
图2
图3
图4
4. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小? 哪个圆柱的体积最大?你有什么发现?
18
12
9
6
2
3
4
6
以长边为周长
以短边为周长
同一个长方形,以长作为底面周长时卷成的圆柱体积大,以宽为底面周长时,卷成的圆柱的体积小
( )
( )
