人教版数学必修3 2.2.2 用样本的数字特征估计总体的数字特征(共30张ppt)
文档属性
| 名称 | 人教版数学必修3 2.2.2 用样本的数字特征估计总体的数字特征(共30张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 472.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 00:00:00 | ||
图片预览








文档简介
课件30张PPT。 §2.2.2用样本的数字特征估计总体的数字特征
众 数在一组数据中,出现次数最多的数据叫做这一组数据的众数.
特征:众数体现了样本数据的最大集中点,它只能表达样本数据中的很少一部分信息。它对其他数据信息的忽视使其无法客观地反映总体特征 。
中 位 数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
特征:一组数据中的中位数是 唯一 的,中位数不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点. 一:众数,中位数,平均数思考:如何对一组样本数据求众数,中位数,平均数?
1,3,5,7,7,9
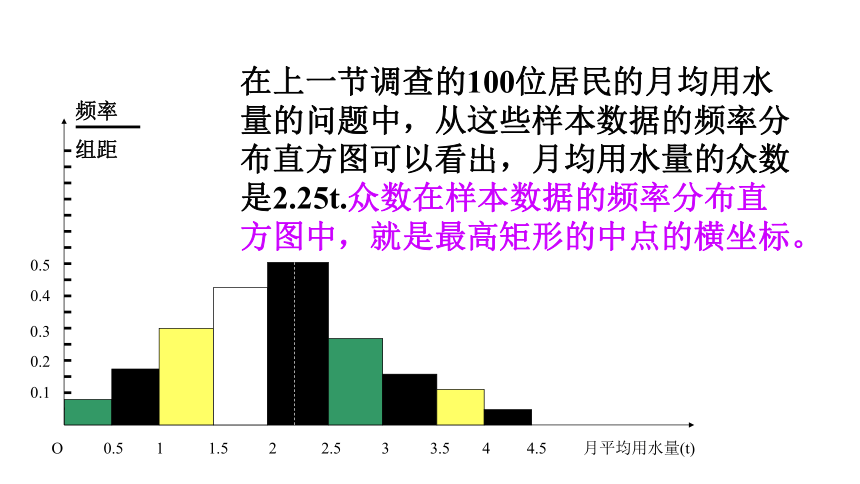
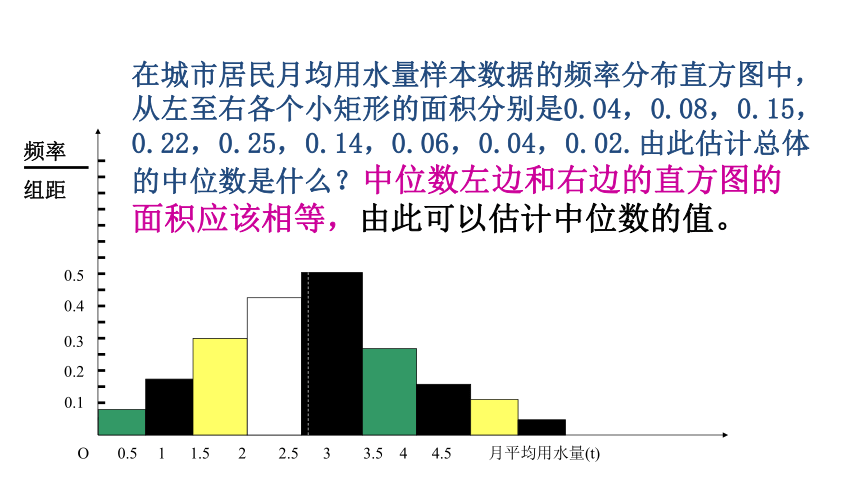
甲在一次射击比赛中的得分如下: ( 单位:环).7, 8, 6, 8, 6, 5, 9, 10, 7, 5,则他命中的平均数是_____,中位数________, 众数是_______________.2. 某次数学试卷得分抽样中得到:90分的有3个人,80分的有10人,70分的有5人,60分的有2人,则这次抽样的平均分为______.7.177分75,6,7,8 二. 如何从频率分布直方图中估计众数、中位数、平均数?众数:最高矩形的中点的横坐标中位数:左右两边直方图的面积相等.平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。在城市居民月均用水量样本数据的频率分布直方图中,从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此估计总体的中位数是什么?中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。 说明:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.在下面的频率分布直方图中,从直方图估计总体在各组数据内的平均数分别为多少?0.25,0.75,1.25,
1.75,2.25,2.75,
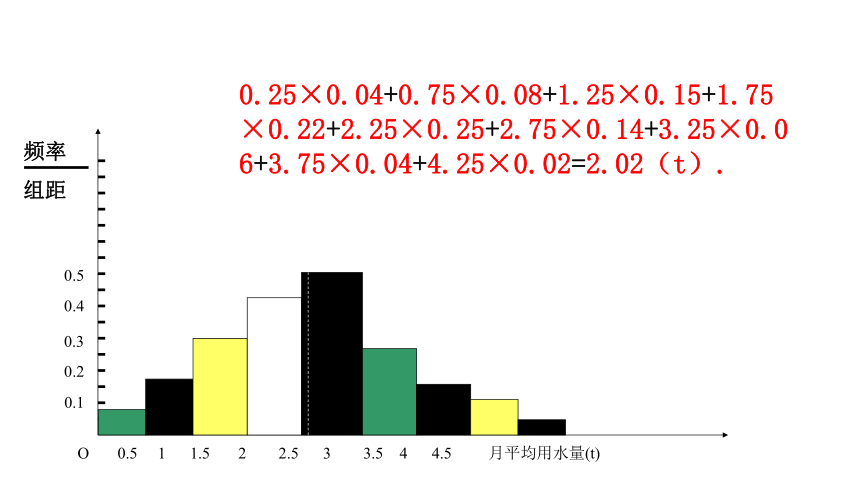
3.25,3.75,4.25. 0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02(t). 三、三种数字特征的优缺点 1、众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少. 2、中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。 3、由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 四、众数、中位数、平均数的简单应用例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么? 解:众数为200,中位数为220,平均数为300。因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息.但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大.课本P74 练习探究 一个企业中, 一线工人的人数很多,他们的月收入是两千左右,然后有少数人员是经理以上层次的人,他们的月收入是三万左右。去招聘时,回答有关工资待遇方面的问题,你更愿意用哪个数字特征来回答这个问题呢? 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,只有平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
五.标准差 标准差是样本数据到平均数的一种平均距离.它用来描述样本数据的离散程度.在应用中,标准差常被理解为稳定性.1、计算标准差的算法:1、算出样本数据的平均数
2、算出每个样本数据与样本平均数的差
3、算出 ,这n个数的平均数的开方,即为样本标准差,标准差的平方叫样本的方差。 注意:1、标准差、方差的取值范围:
当标准差,方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性。
2、方差与标准差在刻画样本数据的离散程度上是一样的,但在解决实际问题时,一般采用标准差。例1:画出下列四组样本数据的条形图,说明它们的异同点.例2:甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm )甲乙从生产的零件内径的尺寸来看,谁生产的质量较高?X甲≈25.401X乙≈25.406s甲≈0.037S乙≈0.068 从样本平均数看,甲生产的零件内径比乙更接近内径标准,且差异很小;
从样本标准差看,由于S甲<S乙,因此甲生产的零件内径比乙的稳定程度高很多。于是,可以作出判断,甲生产的零件的质量比乙的高一些。X甲≈25.401 X乙≈25.406
S甲≈0.037 S乙≈0.068练习:对划艇运动员甲乙二人在相同的条件下进行了6次测试,测得他们最大速度的数据如下:
甲:27,38,30,37,35,31; 乙:33,29,38,34,28,36
根据以上数据,试判断他们谁更优秀。乙比甲更稳定,所以乙比甲更优秀
小结:1. 众数、中位数、平均数的概念
2. 众数、中位数、平均数与频率分布直方图的关系
3. 三种数字特征的优缺点
三种数字特征的优缺点4. 标准差的计算公式?
5. 标准差刻画数据的离散程度?
当堂检测 2010高考题:样本中有五个个体,其值分别为a,0,1,2,3。若该样本的平均值为1,则样本方差为多少?
作业:82页第6题
众 数在一组数据中,出现次数最多的数据叫做这一组数据的众数.
特征:众数体现了样本数据的最大集中点,它只能表达样本数据中的很少一部分信息。它对其他数据信息的忽视使其无法客观地反映总体特征 。
中 位 数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
特征:一组数据中的中位数是 唯一 的,中位数不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点. 一:众数,中位数,平均数思考:如何对一组样本数据求众数,中位数,平均数?
1,3,5,7,7,9
甲在一次射击比赛中的得分如下: ( 单位:环).7, 8, 6, 8, 6, 5, 9, 10, 7, 5,则他命中的平均数是_____,中位数________, 众数是_______________.2. 某次数学试卷得分抽样中得到:90分的有3个人,80分的有10人,70分的有5人,60分的有2人,则这次抽样的平均分为______.7.177分75,6,7,8 二. 如何从频率分布直方图中估计众数、中位数、平均数?众数:最高矩形的中点的横坐标中位数:左右两边直方图的面积相等.平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。在城市居民月均用水量样本数据的频率分布直方图中,从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此估计总体的中位数是什么?中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。 说明:
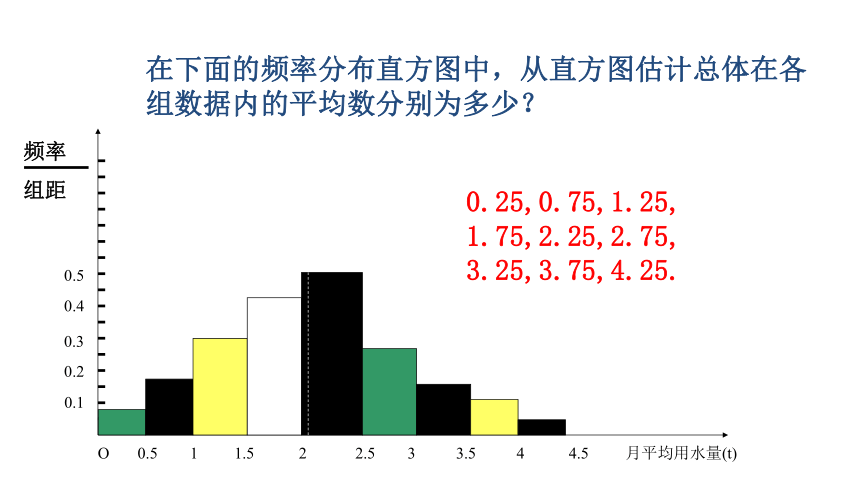
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.在下面的频率分布直方图中,从直方图估计总体在各组数据内的平均数分别为多少?0.25,0.75,1.25,
1.75,2.25,2.75,
3.25,3.75,4.25. 0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02(t). 三、三种数字特征的优缺点 1、众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.如上例中众数是2.25t,它告诉我们,月均用水量为2.25t的居民数比月均用水量为其它数值的居民数多,但它并没有告诉我们多多少. 2、中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点。如上例中假设有某一用户月均用水量为10t,那么它所占频率为0.01,几乎不影响中位数,但显然这一极端值是不能忽视的。 3、由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。也正因如此 ,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。 四、众数、中位数、平均数的简单应用例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么? 解:众数为200,中位数为220,平均数为300。因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息.但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大.课本P74 练习探究 一个企业中, 一线工人的人数很多,他们的月收入是两千左右,然后有少数人员是经理以上层次的人,他们的月收入是三万左右。去招聘时,回答有关工资待遇方面的问题,你更愿意用哪个数字特征来回答这个问题呢? 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,只有平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
五.标准差 标准差是样本数据到平均数的一种平均距离.它用来描述样本数据的离散程度.在应用中,标准差常被理解为稳定性.1、计算标准差的算法:1、算出样本数据的平均数
2、算出每个样本数据与样本平均数的差
3、算出 ,这n个数的平均数的开方,即为样本标准差,标准差的平方叫样本的方差。 注意:1、标准差、方差的取值范围:
当标准差,方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性。
2、方差与标准差在刻画样本数据的离散程度上是一样的,但在解决实际问题时,一般采用标准差。例1:画出下列四组样本数据的条形图,说明它们的异同点.例2:甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm )甲乙从生产的零件内径的尺寸来看,谁生产的质量较高?X甲≈25.401X乙≈25.406s甲≈0.037S乙≈0.068 从样本平均数看,甲生产的零件内径比乙更接近内径标准,且差异很小;
从样本标准差看,由于S甲<S乙,因此甲生产的零件内径比乙的稳定程度高很多。于是,可以作出判断,甲生产的零件的质量比乙的高一些。X甲≈25.401 X乙≈25.406
S甲≈0.037 S乙≈0.068练习:对划艇运动员甲乙二人在相同的条件下进行了6次测试,测得他们最大速度的数据如下:
甲:27,38,30,37,35,31; 乙:33,29,38,34,28,36
根据以上数据,试判断他们谁更优秀。乙比甲更稳定,所以乙比甲更优秀
小结:1. 众数、中位数、平均数的概念
2. 众数、中位数、平均数与频率分布直方图的关系
3. 三种数字特征的优缺点
三种数字特征的优缺点4. 标准差的计算公式?
5. 标准差刻画数据的离散程度?
当堂检测 2010高考题:样本中有五个个体,其值分别为a,0,1,2,3。若该样本的平均值为1,则样本方差为多少?
作业:82页第6题
