四年级上册数学教案-4.5 乘法分配律北师大版
文档属性
| 名称 | 四年级上册数学教案-4.5 乘法分配律北师大版 | 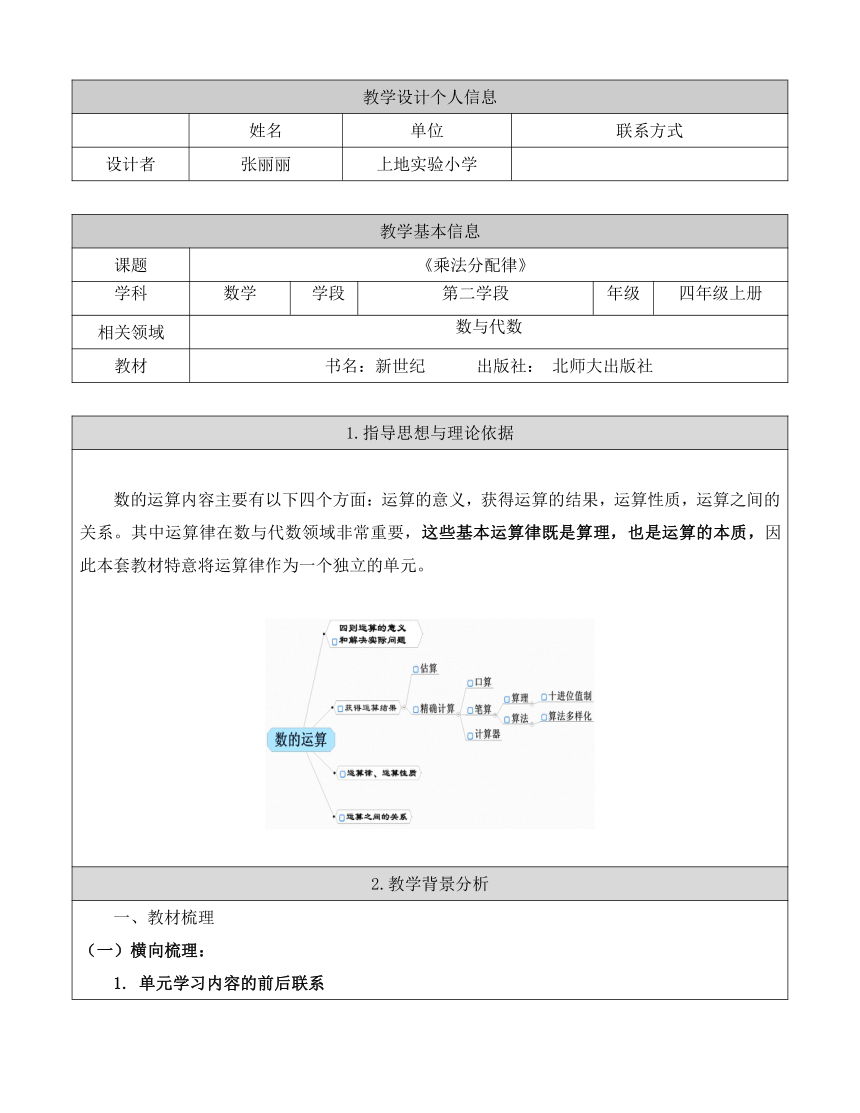 | |
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 14:42:09 | ||
图片预览




文档简介
(
2
)
教学设计个人信息
姓名
单位
联系方式
设计者
张丽丽
上地实验小学
教学基本信息
课题
《乘法分配律》
学科
数学
学段
第二学段
年级
四年级上册
相关领域
数与代数
教材
书名:新世纪
出版社:
北师大出版社
1.指导思想与理论依据
数的运算内容主要有以下四个方面:运算的意义,获得运算的结果,运算性质,运算之间的关系。其中运算律在数与代数领域非常重要,这些基本运算律既是算理,也是运算的本质,因此本套教材特意将运算律作为一个独立的单元。
2.教学背景分析
一、教材梳理
(一)横向梳理:
1.
单元学习内容的前后联系
2.教材呈现方式
教材围绕乘法分配律精心设计了问题串来引导学生自己发现问题,提出问题,归纳和总结规律,积累合情推理的数学活动经验,提升思维能力。
①结合解决实际问题的过程,感受两种不同的列式计算方法___体会算法多样化;
②观察算式、发现乘法分配律总结概括___培养观察、推理能力;
③用字母表示乘法分配律___发展符号意识;
④结合已有经验,解释乘法分配律的正确性___树立模型思想。与前面的运算律的研究模式是一样的。
3.本节课的核心本质:
(1)重视学生个性发展的全过程让学生自主尝试
(2)
积累合情推理的数学活动经验
(3)理解乘法分配律的意义
,把握运算的本质(算式的等值变形)
(二)纵向梳理:
三、我的思考:
1.改变学习方式——学生自主探究
将教材中的问题串进行整合,制成探究学案,放手让学生自主探究。
2.本节课对于学生来说,无论是知识经验、还是活动经验都有丰富的、感性的学习基础,因此这节课可以说是轻车熟路,只需要借助一个直观的模型顺水推舟,让学生经历发现问题——提出问题——归纳总结规律的全过程。关注数学思考,发展合情推理能力。积累合情推理经验,提升思维能力。
3.根据学生的认知特点,引导学生借用图形直观和生活的现实背景理解乘法分配律的意义。
二、学情分析
1.
学生已有的知识基础和活动经验
二年级上
在6-9的乘法口诀中,学生有过这样的学习经历……
三年级上
在长方形周长公式的推导中,学生有过这样的学习经历……
在探究两位数乘法算理的学习中,学生有过这样的学习经历……
我的思考:乘法分配律的结构原理渗透在低年级整数加减和乘法运算中,为总结、归纳乘法分配律提供了最基本的知识原型。而“长方形的周长=(长+宽)×2=长×2
+宽×2”作为乘法分配律的知识原型,更是数形结合、简洁易记。
2.学生调研
调研班级:四(4)42人
调研目的:
学生对于“乘法分配律”的模型基础和知识基础;
学生面对教材问题的解决策略以及难点。
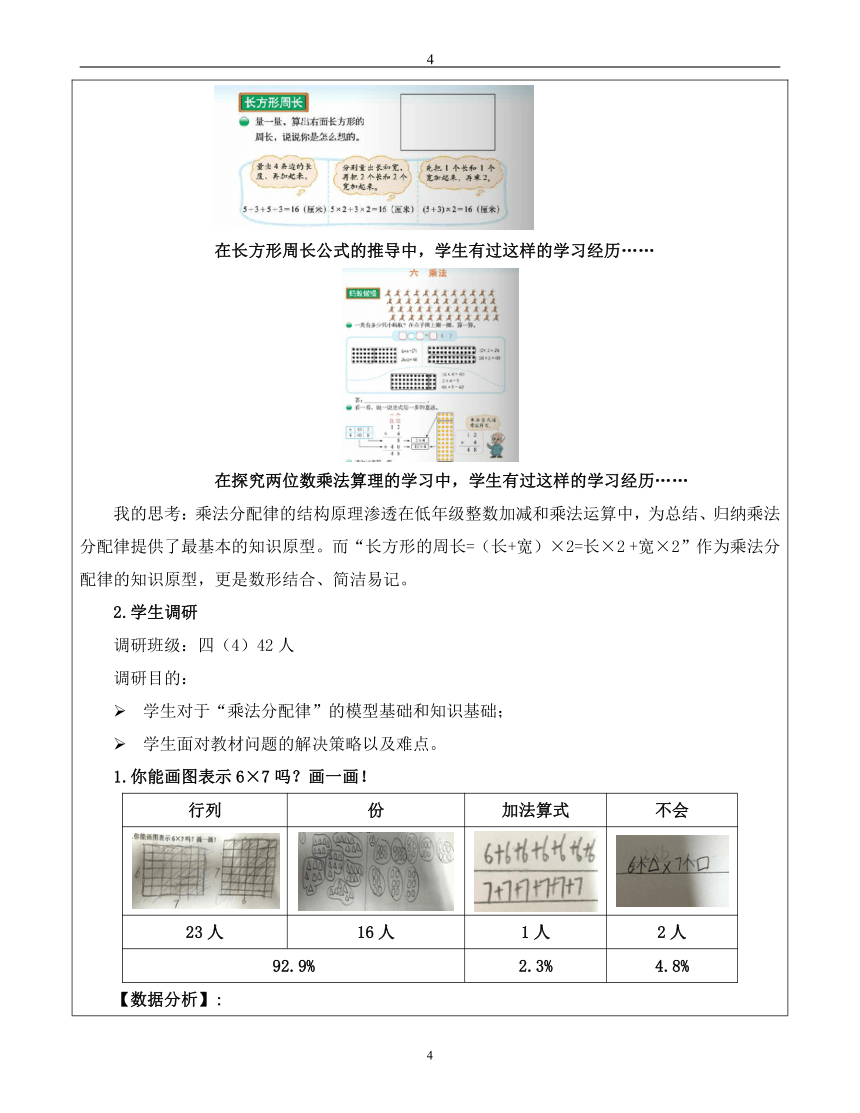
1.你能画图表示6×7吗?画一画!
行列份加法算式不会23人16人1人2人92.9%2.3%4.8%
【数据分析】:
其一,大部分学生头脑中有乘法模型,不管是二维的“行列”,还是一维的“份”,学生对乘法意义掌握的非常好!
其二,既然学生头脑中有那么清晰的乘法模型,我们在设计本节课时,可以以此作为“乘法分配律”的模型基础,从“形”入手,帮助学生理解、建构乘法分配律。
2.贴多少块瓷砖?请你写一写你是怎样算的。(方法不唯一)
6×8+4×8(6+4)×810×810×5+10×33×(4+6)+5×(4+6)2×8×5错误32人5人19人24人8人2人3人92.9%7.1%
【数据分析】:
其一,大部分学生都有方法,能够解决问题,只有3人错误(见学生作品);
其二,学生中出现以上6种对的解决策略,这些策略之间是有内在联系的,教学中如果结合“形”挖掘策略间的内在联系,是不是就是在一步一步地在孩子头脑中形成“乘法分配律”呢?
【调研思考】:
以长方形周长公式为例,让学生从2长+2宽,过渡到(长+宽)×2,对学生来说需要一个漫长的过程,因此,“乘法分配律”不同于其他的运算律,它对学生来说之所以难,是因为运算中牵扯的“量”多,“量”与“量”之间又通过第三个“量”有简便关系,需要学生有很强的“数感”。
因此,这节课如果针对“同一幅图”进行各种“拆解”,再回到这幅图,沟通各种“拆解”之间的联系,就是在培养这种数感。但是,这种数感的建立,需要一个过程,想要学生全员掌握不是一节课就能实现的。
3.你能画图解释9×4+6×9=9×10吗?
份数行列算式字母
13人14人3人1人64.3%9.5%73.8%
不能
11人26.2%
【数据分析】:
其一,大部分学生能够用乘法意义讲清算理,近三分之一的学生不能讲清算理,一小部分学生选择算式或代数式。
其二,课堂中应该设计这样一个教学环节在“正”推运算规律之后,让学生“反”过来用画图讲一讲“乘法分配律”,形成一个“正反”建构运算律模型的过程,从而加深运算律的理解。
【学生错题】
2.贴多少块瓷砖?请你写一写你是怎样算的。(方法不唯一)
3.教学目标(含重、难点)
教学目标:
1.
在解决问题过程中,渗透并感知乘法分配律的本质意义;
2.在多种解题方法的沟通联系中,逐渐建构并推理归纳乘法分配律;
3.通过自学探究学案,在题题独立思考——追忆发现——再思考的探索学习中,感受规律的形成,体验探究规律的乐趣。
教学重点:在解决问题过程中,渗透并感知乘法分配律的本质意义。
教学难点:在多种解题方法的沟通联系中,逐渐建构并推理归纳乘法分配律。
4.教学过程与教学资源设计(可附教学流程图)
教学流程图:
教学过程:
一、出示完整学案,独立思考探究
1.工人叔叔在装修房屋贴瓷砖(如图),
这幅图你怎么看,能懂图的意思吗?
预设:左面墙和右面墙;
白色和蓝色两种瓷砖;
整面墙是一个大长方形。
(板书:左面和右面、白色和蓝色、整体)
2.一共要贴多少块瓷砖,你打算怎么算?
要求:①画简图(标数据)怎么看就怎么画;
②列综合式,怎么画怎么列,简图和算式要一致;
③针对简图,你还可以怎样列不同的综合算式。
3.根据不同思维水平的学生,提供不同的学习单
(
学习单
2
——
自己画
简
图
)
(
学习单1——
给图
)
【设计目的】:将教材中的问题串进行整合,制成探究学案,放手让学生自主探究,提供足够的时间和空间去思考,进一步观察、分析、比较发现规律。
二、小组交流提纲:
1.你们小组求瓷砖的方法有多少种?都合理吗?
2.观察小组内列出的算式,这些方法之间有什么联系呢?说说你们各自有什么发现?
三、集体汇报,构建模型
(一)结合图和综合算式,沟通联系
1.解读算法
问题:从简图中,你能看懂是怎么看这幅图的吗?
结合图,说一说算式的意思。
2.解读联系
问题:这幅图,可以这样列式也可以这样列式,这两组综合算式有什么关系吗?
4×8+6×8
?(4+6)×8
3×10+5×10
?(3+5)×10
预设:相等(为什么相等,试着深度解读其中的奥秘吗?)
结合图:
举例:
小结:4个8+6个8=(4+6)个8
3个10+5个10=(3+5)个10
(二)发现算式特点,概括规律,出乘法分配律课题(图——算式)
1.大量等式和图,发现算式特点
问题:抛开图意,这面墙还可以怎么拆?(图略)
横拆:1个10+7个10=(1+7)个10
1×10+7×10=(1+7)×10
2个10+6个10=(1+7)个10
2×10+6×10=(1+7)×10
3个10+5个10=(1+7)个10
3×10+5×10=(1+7)×10
4个10+4个10=(1+7)个10
4×10+4×10=(1+7)×10
竖拆:1个8+9个8=(1+9)个8
1×8+9×8=(1+9)×8
2个8+8个8=(2+8)个8
2×8+8×8=(2+8)×8
3个8+7个8=(3+7)个8
3×8+7×8=(3+7)×8
4个8+6个8=(4+6)个8
4×8+6×8=(4+6)×8
5个8+5个8=(5+5)个8
5×8+5×8=(5+5)×8
(三)归纳提炼,字母表示
概括通式(如果这面墙这样的呢?)
(
a
)
(
b
)
(
c
)
a×c+b×c=(a+b)×c
a个c+b个c=(a+b)×c
揭示课题,感受乘法分配律的用途
问题:知道今天咱们研究的是什么吗?(出示课题:《乘法分配律》)那咱们研究乘法分配律有用吗?
结合图:这面墙不管拆成什么样,够能归结到整面墙8×10更能好算!
【设计目的】:学生根据图意解读关联的两个算式,数形结合感受等值变形的特点,初步发现规律。在反思左右两边为什么相等的过程中感受数学的严谨性。为学生感受分配律提供了现实背景,从中体会分配律的合理性,简便性。
四、勾起回忆,交流学习感受
1.问题:学到这,你们发现没有,其实乘法分配律这人有点似曾相识的感觉,你能在之前的学习中找到它的影子吗?
①乘法口诀;
②长方形周长公式;
③乘法竖式;
④生活实例。
2.乘法分配律在这节课之前都谁接触过?通过今天的学习你有什么想说的?(深度揭秘乘法分配律)
【设计目的】:通过找影子方式来表达乘法分配律加以内化,从数量关系变化的多次类比中感悟规律。为归纳出一般性的规律奠定基础。
5.学习效果评价设计
你能试着解决下面的问题吗?
6.教学设计特色说明与教学反思
此设计的亮点:
1.在教学中充分体现学生的主体地位,创设一个大的问题情境,让学生经历提出问题、发现问题的全过程。
2.让学生自主抽象、观察、仿写、解释和表达,经历初步发现、解释发现、归纳规律的学习活动,从而理解和掌握乘法分配律,积累合情推理的数学活动经验。
3.课堂三次引导学生对算式为什么可以画等号进行反思,第一次是抽象出等式时,第二次是仿写算式时,第三次是结合情境和图形直观解释规律时,注重了学生反思能力的培养。
4.找影子的环节孩子记忆深刻,在这数学周记中,孩子们这样描述了乘法分配律:
2
11
2
)
教学设计个人信息
姓名
单位
联系方式
设计者
张丽丽
上地实验小学
教学基本信息
课题
《乘法分配律》
学科
数学
学段
第二学段
年级
四年级上册
相关领域
数与代数
教材
书名:新世纪
出版社:
北师大出版社
1.指导思想与理论依据
数的运算内容主要有以下四个方面:运算的意义,获得运算的结果,运算性质,运算之间的关系。其中运算律在数与代数领域非常重要,这些基本运算律既是算理,也是运算的本质,因此本套教材特意将运算律作为一个独立的单元。
2.教学背景分析
一、教材梳理
(一)横向梳理:
1.
单元学习内容的前后联系
2.教材呈现方式
教材围绕乘法分配律精心设计了问题串来引导学生自己发现问题,提出问题,归纳和总结规律,积累合情推理的数学活动经验,提升思维能力。
①结合解决实际问题的过程,感受两种不同的列式计算方法___体会算法多样化;
②观察算式、发现乘法分配律总结概括___培养观察、推理能力;
③用字母表示乘法分配律___发展符号意识;
④结合已有经验,解释乘法分配律的正确性___树立模型思想。与前面的运算律的研究模式是一样的。
3.本节课的核心本质:
(1)重视学生个性发展的全过程让学生自主尝试
(2)
积累合情推理的数学活动经验
(3)理解乘法分配律的意义
,把握运算的本质(算式的等值变形)
(二)纵向梳理:
三、我的思考:
1.改变学习方式——学生自主探究
将教材中的问题串进行整合,制成探究学案,放手让学生自主探究。
2.本节课对于学生来说,无论是知识经验、还是活动经验都有丰富的、感性的学习基础,因此这节课可以说是轻车熟路,只需要借助一个直观的模型顺水推舟,让学生经历发现问题——提出问题——归纳总结规律的全过程。关注数学思考,发展合情推理能力。积累合情推理经验,提升思维能力。
3.根据学生的认知特点,引导学生借用图形直观和生活的现实背景理解乘法分配律的意义。
二、学情分析
1.
学生已有的知识基础和活动经验
二年级上
在6-9的乘法口诀中,学生有过这样的学习经历……
三年级上
在长方形周长公式的推导中,学生有过这样的学习经历……
在探究两位数乘法算理的学习中,学生有过这样的学习经历……
我的思考:乘法分配律的结构原理渗透在低年级整数加减和乘法运算中,为总结、归纳乘法分配律提供了最基本的知识原型。而“长方形的周长=(长+宽)×2=长×2
+宽×2”作为乘法分配律的知识原型,更是数形结合、简洁易记。
2.学生调研
调研班级:四(4)42人
调研目的:
学生对于“乘法分配律”的模型基础和知识基础;
学生面对教材问题的解决策略以及难点。
1.你能画图表示6×7吗?画一画!
行列份加法算式不会23人16人1人2人92.9%2.3%4.8%
【数据分析】:
其一,大部分学生头脑中有乘法模型,不管是二维的“行列”,还是一维的“份”,学生对乘法意义掌握的非常好!
其二,既然学生头脑中有那么清晰的乘法模型,我们在设计本节课时,可以以此作为“乘法分配律”的模型基础,从“形”入手,帮助学生理解、建构乘法分配律。
2.贴多少块瓷砖?请你写一写你是怎样算的。(方法不唯一)
6×8+4×8(6+4)×810×810×5+10×33×(4+6)+5×(4+6)2×8×5错误32人5人19人24人8人2人3人92.9%7.1%
【数据分析】:
其一,大部分学生都有方法,能够解决问题,只有3人错误(见学生作品);
其二,学生中出现以上6种对的解决策略,这些策略之间是有内在联系的,教学中如果结合“形”挖掘策略间的内在联系,是不是就是在一步一步地在孩子头脑中形成“乘法分配律”呢?
【调研思考】:
以长方形周长公式为例,让学生从2长+2宽,过渡到(长+宽)×2,对学生来说需要一个漫长的过程,因此,“乘法分配律”不同于其他的运算律,它对学生来说之所以难,是因为运算中牵扯的“量”多,“量”与“量”之间又通过第三个“量”有简便关系,需要学生有很强的“数感”。
因此,这节课如果针对“同一幅图”进行各种“拆解”,再回到这幅图,沟通各种“拆解”之间的联系,就是在培养这种数感。但是,这种数感的建立,需要一个过程,想要学生全员掌握不是一节课就能实现的。
3.你能画图解释9×4+6×9=9×10吗?
份数行列算式字母
13人14人3人1人64.3%9.5%73.8%
不能
11人26.2%
【数据分析】:
其一,大部分学生能够用乘法意义讲清算理,近三分之一的学生不能讲清算理,一小部分学生选择算式或代数式。
其二,课堂中应该设计这样一个教学环节在“正”推运算规律之后,让学生“反”过来用画图讲一讲“乘法分配律”,形成一个“正反”建构运算律模型的过程,从而加深运算律的理解。
【学生错题】
2.贴多少块瓷砖?请你写一写你是怎样算的。(方法不唯一)
3.教学目标(含重、难点)
教学目标:
1.
在解决问题过程中,渗透并感知乘法分配律的本质意义;
2.在多种解题方法的沟通联系中,逐渐建构并推理归纳乘法分配律;
3.通过自学探究学案,在题题独立思考——追忆发现——再思考的探索学习中,感受规律的形成,体验探究规律的乐趣。
教学重点:在解决问题过程中,渗透并感知乘法分配律的本质意义。
教学难点:在多种解题方法的沟通联系中,逐渐建构并推理归纳乘法分配律。
4.教学过程与教学资源设计(可附教学流程图)
教学流程图:
教学过程:
一、出示完整学案,独立思考探究
1.工人叔叔在装修房屋贴瓷砖(如图),
这幅图你怎么看,能懂图的意思吗?
预设:左面墙和右面墙;
白色和蓝色两种瓷砖;
整面墙是一个大长方形。
(板书:左面和右面、白色和蓝色、整体)
2.一共要贴多少块瓷砖,你打算怎么算?
要求:①画简图(标数据)怎么看就怎么画;
②列综合式,怎么画怎么列,简图和算式要一致;
③针对简图,你还可以怎样列不同的综合算式。
3.根据不同思维水平的学生,提供不同的学习单
(
学习单
2
——
自己画
简
图
)
(
学习单1——
给图
)
【设计目的】:将教材中的问题串进行整合,制成探究学案,放手让学生自主探究,提供足够的时间和空间去思考,进一步观察、分析、比较发现规律。
二、小组交流提纲:
1.你们小组求瓷砖的方法有多少种?都合理吗?
2.观察小组内列出的算式,这些方法之间有什么联系呢?说说你们各自有什么发现?
三、集体汇报,构建模型
(一)结合图和综合算式,沟通联系
1.解读算法
问题:从简图中,你能看懂是怎么看这幅图的吗?
结合图,说一说算式的意思。
2.解读联系
问题:这幅图,可以这样列式也可以这样列式,这两组综合算式有什么关系吗?
4×8+6×8
?(4+6)×8
3×10+5×10
?(3+5)×10
预设:相等(为什么相等,试着深度解读其中的奥秘吗?)
结合图:
举例:
小结:4个8+6个8=(4+6)个8
3个10+5个10=(3+5)个10
(二)发现算式特点,概括规律,出乘法分配律课题(图——算式)
1.大量等式和图,发现算式特点
问题:抛开图意,这面墙还可以怎么拆?(图略)
横拆:1个10+7个10=(1+7)个10
1×10+7×10=(1+7)×10
2个10+6个10=(1+7)个10
2×10+6×10=(1+7)×10
3个10+5个10=(1+7)个10
3×10+5×10=(1+7)×10
4个10+4个10=(1+7)个10
4×10+4×10=(1+7)×10
竖拆:1个8+9个8=(1+9)个8
1×8+9×8=(1+9)×8
2个8+8个8=(2+8)个8
2×8+8×8=(2+8)×8
3个8+7个8=(3+7)个8
3×8+7×8=(3+7)×8
4个8+6个8=(4+6)个8
4×8+6×8=(4+6)×8
5个8+5个8=(5+5)个8
5×8+5×8=(5+5)×8
(三)归纳提炼,字母表示
概括通式(如果这面墙这样的呢?)
(
a
)
(
b
)
(
c
)
a×c+b×c=(a+b)×c
a个c+b个c=(a+b)×c
揭示课题,感受乘法分配律的用途
问题:知道今天咱们研究的是什么吗?(出示课题:《乘法分配律》)那咱们研究乘法分配律有用吗?
结合图:这面墙不管拆成什么样,够能归结到整面墙8×10更能好算!
【设计目的】:学生根据图意解读关联的两个算式,数形结合感受等值变形的特点,初步发现规律。在反思左右两边为什么相等的过程中感受数学的严谨性。为学生感受分配律提供了现实背景,从中体会分配律的合理性,简便性。
四、勾起回忆,交流学习感受
1.问题:学到这,你们发现没有,其实乘法分配律这人有点似曾相识的感觉,你能在之前的学习中找到它的影子吗?
①乘法口诀;
②长方形周长公式;
③乘法竖式;
④生活实例。
2.乘法分配律在这节课之前都谁接触过?通过今天的学习你有什么想说的?(深度揭秘乘法分配律)
【设计目的】:通过找影子方式来表达乘法分配律加以内化,从数量关系变化的多次类比中感悟规律。为归纳出一般性的规律奠定基础。
5.学习效果评价设计
你能试着解决下面的问题吗?
6.教学设计特色说明与教学反思
此设计的亮点:
1.在教学中充分体现学生的主体地位,创设一个大的问题情境,让学生经历提出问题、发现问题的全过程。
2.让学生自主抽象、观察、仿写、解释和表达,经历初步发现、解释发现、归纳规律的学习活动,从而理解和掌握乘法分配律,积累合情推理的数学活动经验。
3.课堂三次引导学生对算式为什么可以画等号进行反思,第一次是抽象出等式时,第二次是仿写算式时,第三次是结合情境和图形直观解释规律时,注重了学生反思能力的培养。
4.找影子的环节孩子记忆深刻,在这数学周记中,孩子们这样描述了乘法分配律:
2
11
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
