2020春粤教版高中物理必修二第三章章末复习课
文档属性
| 名称 | 2020春粤教版高中物理必修二第三章章末复习课 |  | |
| 格式 | zip | ||
| 文件大小 | 377.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-28 17:51:40 | ||
图片预览




文档简介
章末复习课
【知识体系】
[答案填写] ①质量乘积 ②二次方 ③G ④匀速圆周运动 ⑤F向=F引 ⑥ ⑦mω2r ⑧mr ⑨4mπ2rf2 ⑩7.9 km/s ?11.2 km/s ?16.7 km/s ?赤道 ?24 h
主题一 近地卫星、同步卫星和赤道上随地球自转的物体三种匀速圆周运动的特征
1.动力学规律:近地卫星和同步卫星都只受万有引力作用,由万有引力充当向心力,满足万有引力充当向心力所决定的天体运行规律.赤道上的物体由于受到地面支持力的作用,是万有引力的分力充当向心力,它的运动规律不同于卫星的运动规律.
2.轨道半径:近地卫星与赤道上物体的轨道半径相同,同步卫星的轨道半径较大,则有r同>r近=r物=R地.
3.运动的线速度:由v=ωr知同步卫星的线速度大于赤道上物体的线速度;由v=,近地卫星的线速度大于同步卫星的线速度,则有v近>v同>v物.
4.运行周期:同步卫星与赤道上物体的运行周期相同.由T=2π,可知近地卫星的周期要小于同步卫星的周期,则有T近<T同=T物.
5.卫星的向心加速度与物体随地球自转的向心加速度的区别.
项目内容 卫星的向心加速度 物体随地球自转的向心加速度
产生原因 由万有引力产生 万有引力的一个分力(另一分力为重力)产生
方向 指向地心 垂直指向地轴
大小 a=g′=(地面附近a近似等于g) a=rω,r为地面上某点到地轴的距离,ω为地球自转角速度
特点 随物体到地心的距离增大而减小 从赤道到两极逐渐减小
【典例1】 (多选)同步卫星离地距离为r,运行速度为v1,加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则( )
A.= B.=
C.= D.=
解析:第一宇宙速度v2即为近地卫星绕地球转动的环绕速度,与同步卫星均满足公式G=m,则有v=,故=,D项正确,C项错误;地球赤道上的物体和同步卫星有相同的角速度ω,由a=ω2r得=,故A项正确,B项错误.
答案:AD
针对训练
1.有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b在地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图所示,则有( )
A.a的向心加速度等于重力加速度g
B.b在相同时间内转过的弧长最长
C.c在4小时内转过的圆心角是
D.d的运动周期有可能是20小时
解析:对a:-FN=ma,又FN>0,=mg,故a
主题二 天体运动中的双星问题
1.概念.
两颗星体靠得很近,但与其他天体相距较远,它们绕连线上的某点做匀速圆周运动,这样的系统称为双星系统.
2.特点.
(1)双星都绕着连线上的一点做匀速圆周运动,每一颗星各自做匀速圆周运动所需的向心力由两颗星间的万有引力提供.
(2)双星可认为是同轴转动,周期相同,角速度相同.
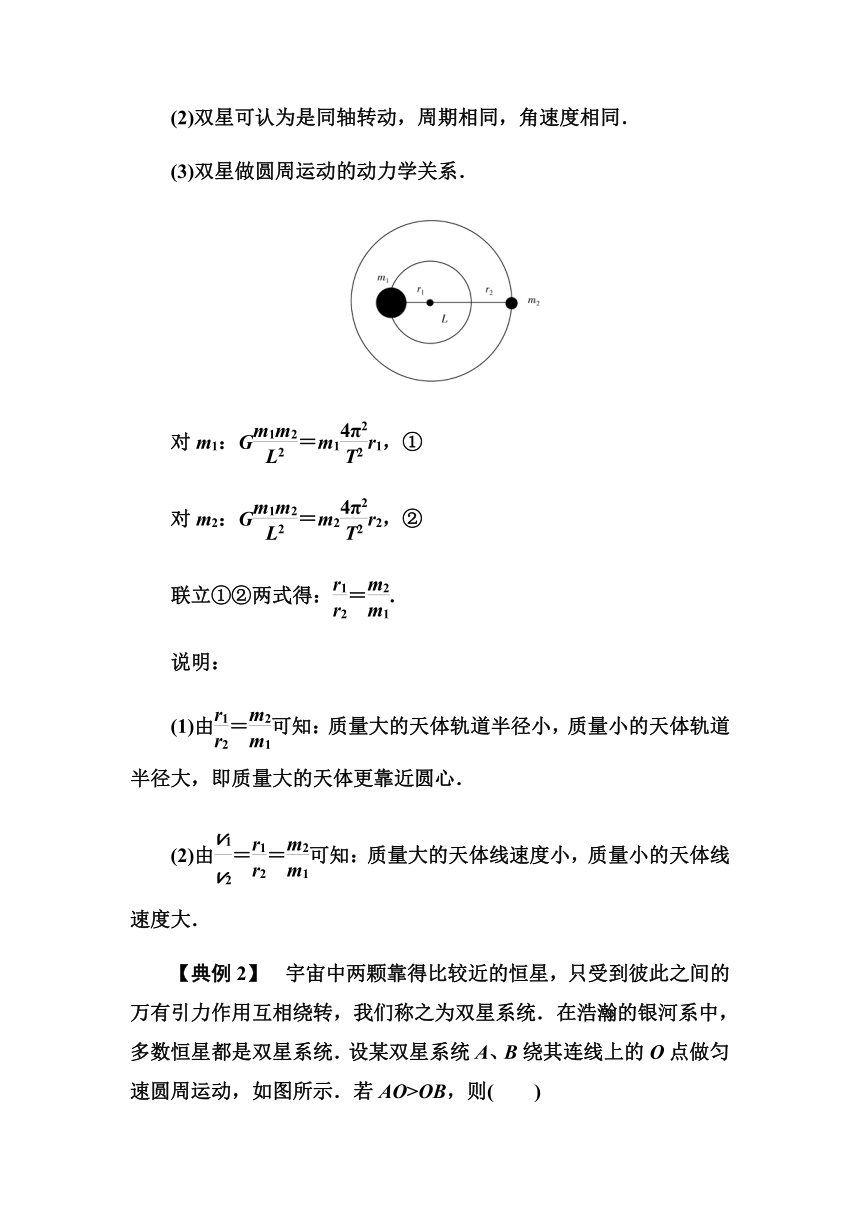
(3)双星做圆周运动的动力学关系.
对m1:G=m1r1,①
对m2:G=m2r2,②
联立①②两式得:=.
说明:
(1)由=可知:质量大的天体轨道半径小,质量小的天体轨道半径大,即质量大的天体更靠近圆心.
(2)由==可知:质量大的天体线速度小,质量小的天体线速度大.
【典例2】 宇宙中两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,我们称之为双星系统.在浩瀚的银河系中,多数恒星都是双星系统.设某双星系统A、B绕其连线上的O点做匀速圆周运动,如图所示.若AO>OB,则( )
A.星球A的角速度一定大于B的角速度
B.星球A的质量一定小于B的质量
C.双星的总质量一定,双星之间的距离越小,其转动周期越大
D.双星之间的距离一定,双星的总质量越大,其转动周期越大
解析:双星靠相互间的万有引力提供向心力,故向心力相等;根据万有引力提供向心力公式得:=mAω2rA=mBω2rB,因为rB
答案:B
题后反思
双星模型的特点及处理方法
1.双星模型的特点.
(1)三点共线:双星模型中的两颗星和它们轨道的圆心O总是在一条直线上.
(2)角速度相同:由于双星模型“三点共线”特点,双星做匀速圆周运动的角速度必然相等,周期也必然相同.
(3)向心力相等:每颗星的向心力都是由双星间相互作用的万有引力提供的,大小相等.
(4)两星的运动半径之和等于它们间的距离,即r1+r2=L.
2.双星模型问题的处理方法:由G=m1ω2r1=m2ω2r2,可得以下结论:
(1)m1r1=m2r2,即运动半径与自身质量成反比.
(2)由于ω=,r1+r2=L,所以双星的质量之和m1+m2=.
针对训练
2.两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动.不考虑其他天体的作用力,下列说法不正确的是( )
A.质量大的天体线速度较小
B.两天体的角速度总是相同
C.若两天体的距离不变,则周期也不变
D.若在圆心处放一个质点,它受到的合力为零
解析:双星系统的结构是稳定的,故它们的角速度与周期相等,选项B正确;设它们的质量分别为m1、m2,距离为L,轨道半径分别为r1、r2,则有G=m1ω2r1=m2ω2r2,得m1r1=m2r2,可知质量大的天体轨道半径较小,又v=ωr,可知其线速度较小,选项A正确;同理可得:G=ω2r1,G=ω2r2;联立以上两式可得G=ω2(r1+r2)=ω2L,可知只要两天体的距离不变,则角速度不变,周期不变,故C正确;结合前面的分析可得,若在圆心放一个质点,设质点的质量为m0,则质点所合力为F=eq \f(Gm1m0,r)-eq \f(Gm2m0,r)=Geq \b\lc\(\rc\)(\a\vs4\al\co1(\f(m1,m)-\f(m2,m)))≠0,故D错误.
答案:D
统揽考情
本章的主线是万有引力定律在天体、航天技术中的应用,在高考考查中属于每年必考内容,在全国卷中一般只考查一道选择题,占6分,命题的热点主要是万有引力定律的理解,还有利用万有引力定律求天体的质量、密度,利用万有引力提供向心力分析航天器、卫星的运行规律.在试题中,有时也考查双星模型与能量综合等问题.
真题例析
(2019·江苏卷)1970年成功发射的“东方红一号”是我国第一颗人造地球卫星,该卫星至今仍沿椭圆轨道绕地球运动.如图所示,设卫星在近地点、远地点的速度分别为v1、v2,近地点到地心的距离为r,地球质量为M,引力常量为G.则( )
A.v1>v2,v1=
B.v1>v2,v1>
C.v1
解析:“东方红一号”从近地点到远地点过程中速度减小,所以v1>v2,过近地点圆周运动的速度为v=,由于“东方红一号”在椭圆上运动,所以v1>,故B正确.
答案:B
针对训练
(2019·全国卷Ⅲ)金星、地球和火星绕太阳的公转均可视为匀速圆周运动,它们的向心加速度大小分别为a金、a地、a火,它们沿轨道运行的速率分别为v金、v地、v火.已知它们的轨道半径R金
B.a火>a地>a金
C.v地>v火>v金
D.v火>v地>v金
解析:由万有引力提供向心力G=ma,可知轨道半径越小,向心加速度越大,故知A项正确,B错误;由G=m,得v=,可知轨道半径越小,运行速率越大,故C、D都错误.
答案:A
1.(2019·北京卷)2019年5月17日,我国成功发射第45颗北斗导航卫星,该卫星属于地球静止轨道卫星(同步卫星).该卫星( )
A.入轨后可以位于北京正上方
B.入轨后的速度大于第一宇宙速度
C.发射速度大于第二宇宙速度
D.若发射到近地圆轨道所需能量较少
解析:由于卫星为同步卫星,所以入轨后一定只能与赤道在同一平面内,故A错误;由于第一宇宙速度为卫星绕地球运行的最大速度,所以卫星入轨后的速度一定小于第一宇宙速度,故B错误;由于第二宇宙速度为卫星脱离地球引力的最小发射速度,所以卫星的发射速度一定小于第二宇宙速度,故C错误;将卫星发射到越高的轨道克服引力所做的功越大,所以发射到近地圆轨道所需能量较小,故D正确.
答案:D
2.(2019·海南卷)2019年5月,我国第45颗北斗卫星发射成功.已知该卫星轨道距地面的高度约为36 000 km,是“天宫二号”空间实验室轨道高度的90倍左右,则( )
A.该卫星的速率比“天宫二号”的大
B.该卫星的周期比“天宫二号”的大
C.该卫星的角速度比“天宫二号”的大
D.该卫星的向心加速度比“天宫二号”的大
解析:根据G=mrω2=mr=m=ma,解得:v=,T=2π,ω=,a=.因北斗卫星的运转半径大于天宫二号的轨道半径,可知该卫星的速率比“天宫二号”的小;该卫星的周期比“天宫二号”的大;该卫星的角速度比“天宫二号”的小;该卫星的向心加速度比“天宫二号”的小,故选项B正确,A、C、D错误.
答案:B
3.(2018·北京卷)若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律,在已知月地距离约为地球半径60倍的情况下,需要验证( )
A.地球吸引月球的力约为地球吸引苹果的力的
B.月球公转的加速度约为苹果落向地面加速度的
C.自由落体在月球表面的加速度约为地球表面的
D.苹果在月球表面受到的引力约为在地球表面的
解析:若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律——万有引力定律,则应满足=ma,即加速度a与距离r的平方成反比,由题中数据知,选项B正确,选项A、C、D错误.
答案:B
4.(多选)(2018·天津卷)2018年2月2日,我国成功将电磁监测试验卫星“张衡一号”发射升空,标志我国成为世界上少数拥有在轨运行高精度地球物理场探测卫星的国家之一.通过观测可以得到卫星绕地球运动的周期,并已知地球的半径和地球表面处的重力加速度.若将卫星绕地球的运动看作是匀速圆周运动,且不考虑地球自转的影响,根据以上数据可以计算出卫星的( )
A.密度 B.向心力的大小
C.离地高度 D.线速度的大小
解析:卫星做圆周运动的向心力由万有引力提供,则有=m2(R+h),无法计算得到卫星的质量,更无法确定其密度及向心力大小,A、B项错误;又=m0g,联立两式可得h=-R,C项正确;由v=,可计算出卫星的线速度的大小,D项正确.
答案:CD
5.(多选)2018年12月8日,肩负着亿万中华儿女探月飞天梦想的嫦娥四号探测器成功发射,“实现人类航天器首次在月球背面巡视探测,率先在月背刻上了中国足迹”.已知月球的质量为M、半径为R,探测器的质量为m,引力常量为G,嫦娥四号探测器围绕月球做半径为r的匀速圆周运动时,探测器的( )
A.周期为2π B.速度为v=
C.角速度为 D.向心加速度为
解析:由万有引力提供向心力可得:=mr=mω2r=m=ma,解得T=2π ,故A正确;解得v=,故B正确;解得ω=,故C错误;解得a=,故D错误.
答案:AB
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
