数学人教四(下)总复习课时3(19张PPT)
文档属性
| 名称 | 数学人教四(下)总复习课时3(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 781.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 00:00:00 | ||
图片预览



文档简介
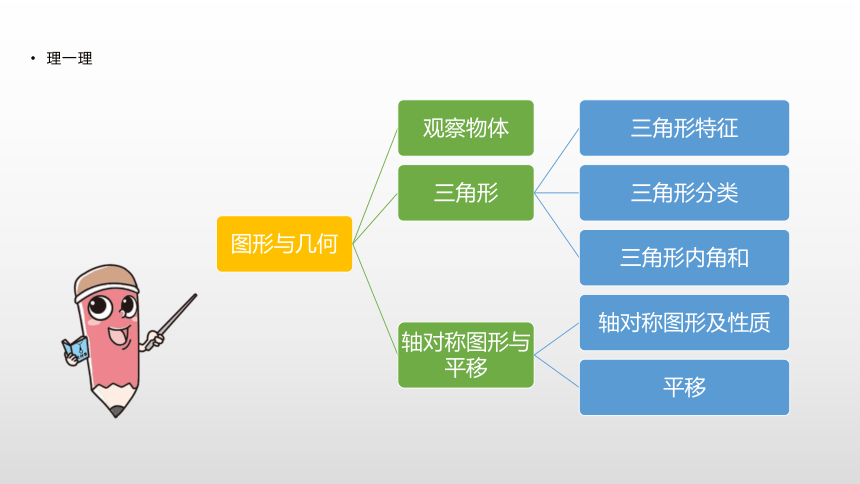
课件19张PPT。总复习第3课时 图形与几何1.巩固轴对称图形的性质和对称轴的画法,能够正确地挑出轴对称图形以及对于不同(组合)图形对称轴的寻找,并能补全轴对称图形。巩固对于平移的知识掌握,并能画出平移后的图形,并利用平移的知识解决问题。
2.巩固三角形的特点和特性,三角形的分类,等腰三角形的特点和三角形三边关系的综合应用,三角形的内角和;综合应用三角形的内角和,等腰三角形的特点等知识解决问题。关注对三角形内角和、三边关系、等边、等腰三角形的特点
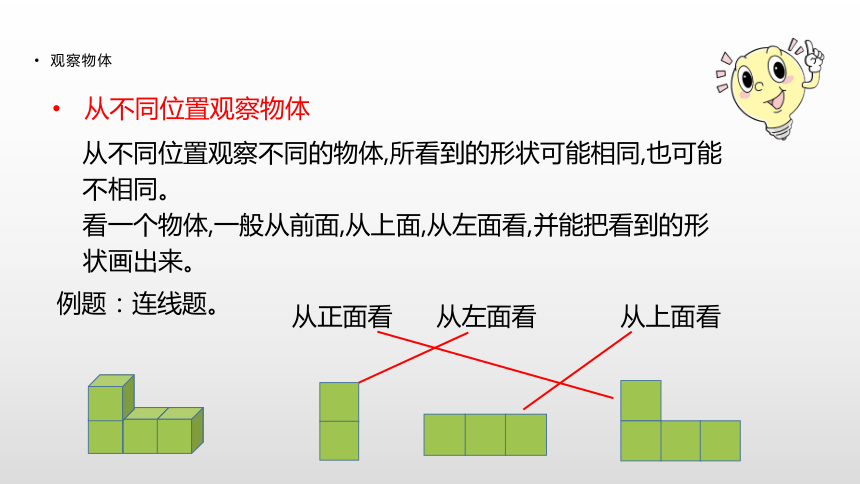
的综合应用。对对称轴与平移知识的应用、空间观念的培养。利用特殊三角形的特点解决问题;空间观念的形成。理一理观察物体从不同位置观察物体从不同位置观察不同的物体,所看到的形状可能相同,也可能
不相同。
看一个物体,一般从前面,从上面,从左面看,并能把看到的形
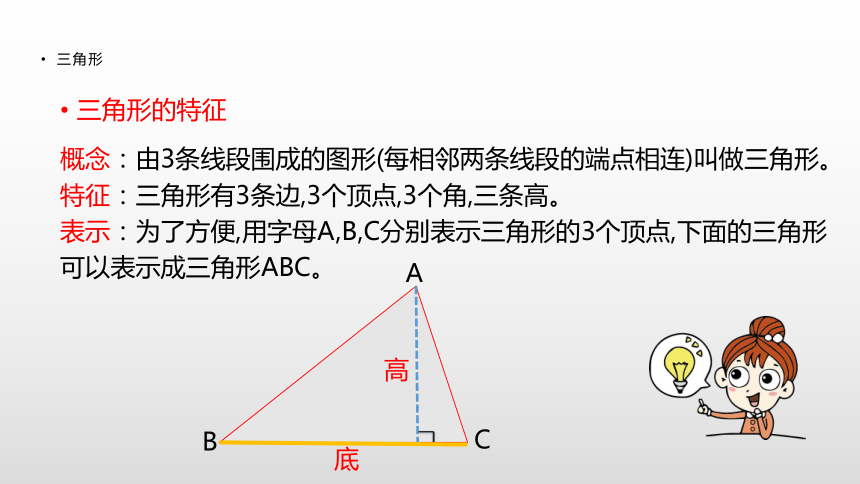
状画出来。例题:连线题。从正面看从左面看从上面看三角形三角形的特征概念:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
特征:三角形有3条边,3个顶点,3个角,三条高。
表示:为了方便,用字母A,B,C分别表示三角形的3个顶点,下面的三角形
可以表示成三角形ABC。ABC底高三角形三角形的特征三边关系:三角形三边关系:三角形任意两边之和大于第三边。任意两
边之差小于第三边。
三角形具有稳定性。例题:在能拼成三角形的一组数后打√,不能的打×。
3 cm,4 cm,5 cm。 ( )
2 cm,2 cm,5 cm。 ( )
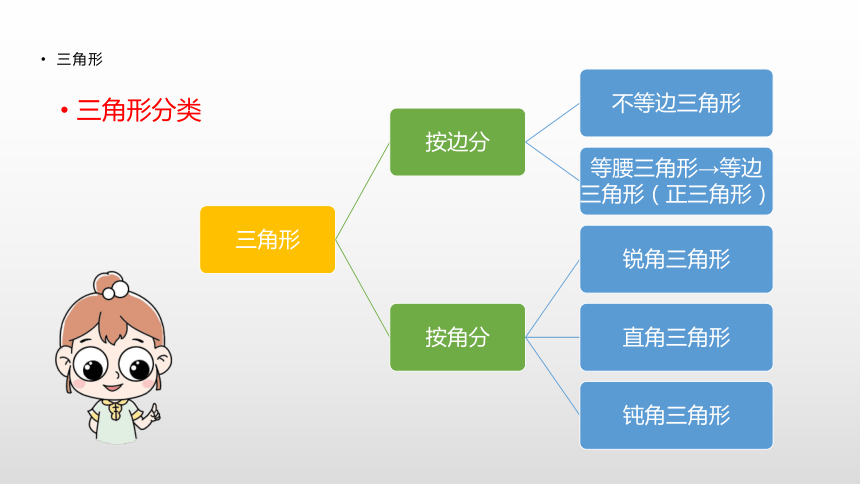
3 cm,3 cm,5 cm。 ( )√×√三角形三角形分类三角形三角形的内角和三角形三个内角之和叫做三角形的内角和,三角形的内角和等于180°。
四边形可以分割成两个三角形,所以四边形的内角和是360°。例题:判断:在能组成三角形的三个角后面括号里画√,不能组成三角形的画×。
①40°,45°,70°。 ( )
②60°,50°,60°。 ( )
③80°,20°,80°。 ( )×√×轴对称图形与平移
轴对称图形的性质:
①对称轴与对称点间的连线互相垂直;
②对应点到对称轴的距离相等。
轴对称图形的画法
轴对称图形与平移
平移
平移不改变物体的形状和大小,只是位置发生变化。;
平移的两个要素:方向和距离。
在方格纸上平移图形的方法1(1)判断
①用三条线段肯定能围成一个三角形。( )
②每个三角形中至多有一个锐角。 ( )
③有一个角是锐角的三角形是锐角三角形。 ( )
(2)一个三角形只有两个锐角,那么这个三角形是一个( )三角形。
A.钝角 B.直角 C.钝角或直角
(3)画一个腰长是3cm的等腰直角三角形。×××C2(1)三角形按角分类有( )、( )和( );
按边分类有不等边三角形,( )三角形和( )三角形。
(2)一个等腰三角形两条边的长度分别是3厘米、6厘米,这
个等腰三角形的周长是( )厘米。
(3)等腰三角形的一个内角是60°,其他两个内角各是( )
度和( )度,这是( )三角形。锐角三角形直角三角形钝角三角形等腰等边1560等边603求未知角的度数。
180°-35°-49°=96°180°-45°-101°=34°180°-90°-24°=66°4(1)小汽车向( )平移了( )格;小船向( )平移了( )格;
小飞机向( )平移了( )格。
(2)把图形向左平移5格后得到( )图形。
右 8 左7上4B51.在一个三角形中,一个锐角是65°,另外两个角可能是( )。
A.95°和20° B.45°和80°
C.65°和60° D.30°和90°
2.在一个三角形中,最大的角是锐角,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
3.有两根木条,它们的长分别为30厘米和50厘米,如果要再选一根木
条做成一个三角形木架,那么应选取( )长的木条。
A.20厘米 B.30厘米 C.80厘米 D.90厘米AAB6计算下面各角的度数。
(1)已知∠1=48°,求∠2。
(2)已知∠1=58°,∠2=65°,求∠3。
∠3=180°-65°-58°
=57°∠2=180°-90°-48°
=42°先根据对称轴补全下面这个轴对称图形,再画出向右平移14格后的图形。7准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼
摆起来,然后填写下表。132435465768……规律:三角形的个数+2=拼成图形周长的厘米数8规律:三角形的个数+2=拼成图形周长的厘米数121029准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼
摆起来,然后填写下表。
2.巩固三角形的特点和特性,三角形的分类,等腰三角形的特点和三角形三边关系的综合应用,三角形的内角和;综合应用三角形的内角和,等腰三角形的特点等知识解决问题。关注对三角形内角和、三边关系、等边、等腰三角形的特点
的综合应用。对对称轴与平移知识的应用、空间观念的培养。利用特殊三角形的特点解决问题;空间观念的形成。理一理观察物体从不同位置观察物体从不同位置观察不同的物体,所看到的形状可能相同,也可能
不相同。
看一个物体,一般从前面,从上面,从左面看,并能把看到的形
状画出来。例题:连线题。从正面看从左面看从上面看三角形三角形的特征概念:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
特征:三角形有3条边,3个顶点,3个角,三条高。
表示:为了方便,用字母A,B,C分别表示三角形的3个顶点,下面的三角形
可以表示成三角形ABC。ABC底高三角形三角形的特征三边关系:三角形三边关系:三角形任意两边之和大于第三边。任意两
边之差小于第三边。
三角形具有稳定性。例题:在能拼成三角形的一组数后打√,不能的打×。
3 cm,4 cm,5 cm。 ( )
2 cm,2 cm,5 cm。 ( )
3 cm,3 cm,5 cm。 ( )√×√三角形三角形分类三角形三角形的内角和三角形三个内角之和叫做三角形的内角和,三角形的内角和等于180°。
四边形可以分割成两个三角形,所以四边形的内角和是360°。例题:判断:在能组成三角形的三个角后面括号里画√,不能组成三角形的画×。
①40°,45°,70°。 ( )
②60°,50°,60°。 ( )
③80°,20°,80°。 ( )×√×轴对称图形与平移
轴对称图形的性质:
①对称轴与对称点间的连线互相垂直;
②对应点到对称轴的距离相等。
轴对称图形的画法
轴对称图形与平移
平移
平移不改变物体的形状和大小,只是位置发生变化。;
平移的两个要素:方向和距离。
在方格纸上平移图形的方法1(1)判断
①用三条线段肯定能围成一个三角形。( )
②每个三角形中至多有一个锐角。 ( )
③有一个角是锐角的三角形是锐角三角形。 ( )
(2)一个三角形只有两个锐角,那么这个三角形是一个( )三角形。
A.钝角 B.直角 C.钝角或直角
(3)画一个腰长是3cm的等腰直角三角形。×××C2(1)三角形按角分类有( )、( )和( );
按边分类有不等边三角形,( )三角形和( )三角形。
(2)一个等腰三角形两条边的长度分别是3厘米、6厘米,这
个等腰三角形的周长是( )厘米。
(3)等腰三角形的一个内角是60°,其他两个内角各是( )
度和( )度,这是( )三角形。锐角三角形直角三角形钝角三角形等腰等边1560等边603求未知角的度数。
180°-35°-49°=96°180°-45°-101°=34°180°-90°-24°=66°4(1)小汽车向( )平移了( )格;小船向( )平移了( )格;
小飞机向( )平移了( )格。
(2)把图形向左平移5格后得到( )图形。
右 8 左7上4B51.在一个三角形中,一个锐角是65°,另外两个角可能是( )。
A.95°和20° B.45°和80°
C.65°和60° D.30°和90°
2.在一个三角形中,最大的角是锐角,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
3.有两根木条,它们的长分别为30厘米和50厘米,如果要再选一根木
条做成一个三角形木架,那么应选取( )长的木条。
A.20厘米 B.30厘米 C.80厘米 D.90厘米AAB6计算下面各角的度数。
(1)已知∠1=48°,求∠2。
(2)已知∠1=58°,∠2=65°,求∠3。
∠3=180°-65°-58°
=57°∠2=180°-90°-48°
=42°先根据对称轴补全下面这个轴对称图形,再画出向右平移14格后的图形。7准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼
摆起来,然后填写下表。132435465768……规律:三角形的个数+2=拼成图形周长的厘米数8规律:三角形的个数+2=拼成图形周长的厘米数121029准备若干个边长为1cm的等边三角形,并按下图所示一个接一个地拼
摆起来,然后填写下表。
