人教版九年级下数学教学讲义,复习补习资料(巩固练习):50【提高】反比例函数含答案
文档属性
| 名称 | 人教版九年级下数学教学讲义,复习补习资料(巩固练习):50【提高】反比例函数含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 15:43:50 | ||
图片预览


文档简介
反比例函数(提高)
【学习目标】
1. 理解反比例函数的概念和意义,能根据问题的反比例关系确定函数解析式.
2. 能根据解析式画出反比例函数的图象,初步掌握反比例函数的图象和性质.
3. 会用待定系数法确定反比例函数解析式,进一步理解反比例函数的图象和性质.
4. 会解决一次函数和反比例函数有关的问题.
【巩固练习】
一.选择题
1. 在反比例函数/的图象上有两点A/,B/,当/时,有/,则/的取值范围是( )
A./ B./ C./ D./
2. 如图所示的图象上的函数关系式只能是( ) .
A. B. C. D.
/
3. 已知,点P()在反比例函数的图像上,则直线不经过的象限是( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 在函数(为常数)的图象上有三个点,,,则函数值、、的大小关系是( ).
A.<< B.<< C.<< D.<<
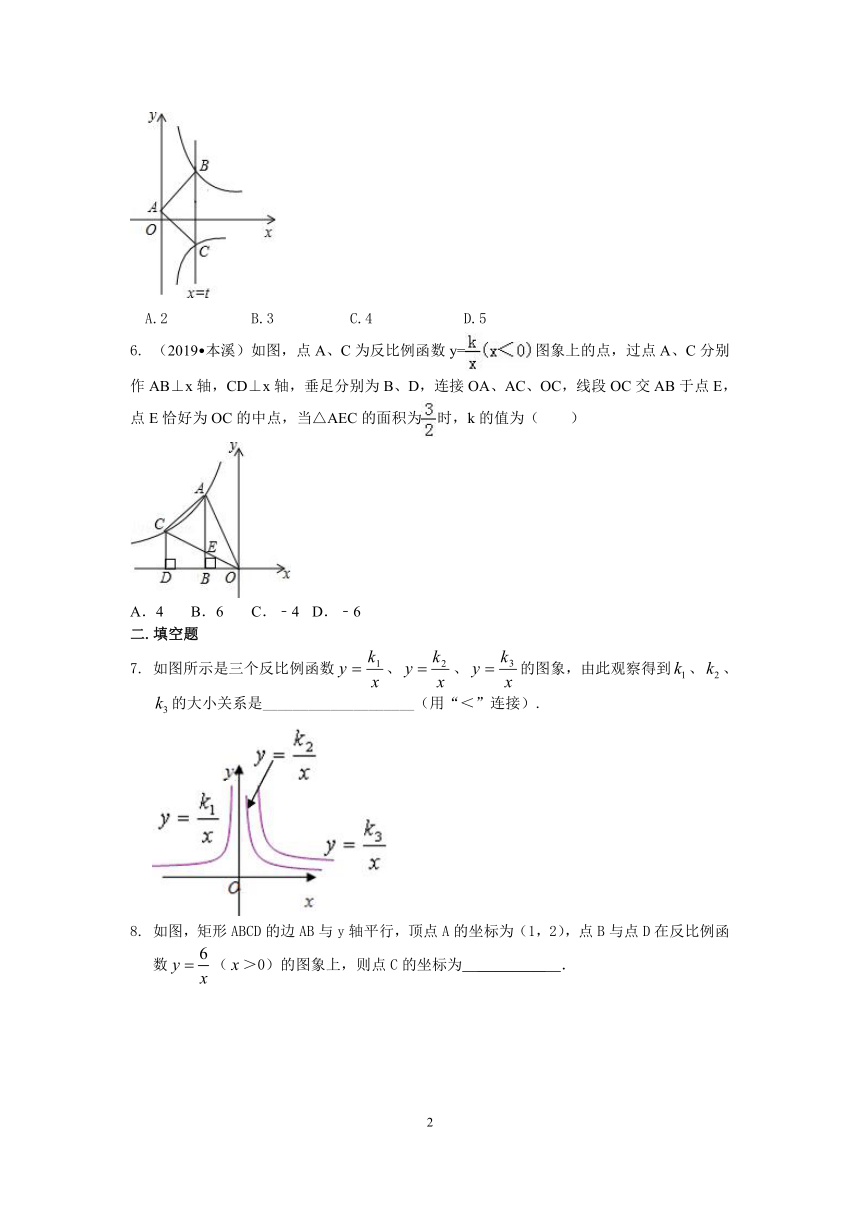
5. (2019?历下区模拟)如图,直线x=t(t>0)与反比例函数y=/(x>0)、y=/(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
/
A.2 B.3 C.4 D.5
6. (2019?本溪)如图,点A、C为反比例函数y=/图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为/时,k的值为( )
/
A.4 B.6 C.﹣4 D.﹣6
二.填空题
7. 如图所示是三个反比例函数、、的图象,由此观察得到、、的大小关系是____________________(用“<”连接).
/
8. 如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数(>0)的图象上,则点C的坐标为 _________ .
/
9. (2019春?江都市校级期末)已知y1与x成正比例(比例系数为k1),y2与x成反比例(比例系数为k2),若函数y=y1+y2的图象经过点(1,2),(2,/),则8k1+5k2的值为 .
10.已知A(),B()都在 图象上.若,则的值为 _________ .
11. 如图,正比例函数的图象与反比例函数(>0)的图象交于点A,若取1,2,3…20,对应的Rt△AOB的面积分别为,则
= ________.
/
12. 如图所示,点,,在x轴上,且,分别过点,, 作轴的平行线,与反比例函数=(>0)的图象分别交于点,,,分别过点,,作轴的平行线,分别于轴交于点,,,连接,,,那么图中阴影部分的面积之和为____________.
/
三.解答题
13. (2019?泉州)已知反比例函数的图象经过点P(2,﹣3).
(1)求该函数的解析式;
(2)若将点P沿x轴负方向平移3个单位,再沿y轴方向平移n(n>0)个单位得到点P′,使点P′恰好在该函数的图象上,求n的值和点P沿y轴平移的方向.
14. 如图所示,已知双曲线与直线相交于A、B两点.第一象限上的点M(,)(在A点左侧)是双曲线上的动点.过点B作BD∥轴交于x轴于点D.过N(0,-)作NC∥轴交双曲线于点E,交BD于点C.
/
(1)若点D坐标是(-8,0),求A、B两点坐标及的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
15. (2019春?耒阳市校级月考)如图,已知点A(﹣8,n),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积,
(3)求方程kx+b﹣=0的解(请直接写出答案);
(4)求不等式kx+b﹣>0的解集(请直接写出答案).
/
【答案与解析】
一.选择题
1.【答案】C;
【解析】由题意画出图象,只能在一、三象限,故.
2.【答案】D;
【解析】画出的图象,再把轴下方的图象翻折上去.
3.【答案】C;
【解析】由题意,故>0,直线经过一、二、四象限.
4.【答案】D;
【解析】,故图象在二、四象限,画出图象,比较大小得D答案.
5.【答案】D;
【解析】解:由题意得,点C的坐标(t,﹣/),点B的坐标(t,/),
BC=/+/,则/(/+/)×t=3,解得k=5,
故选:D.
6.【答案】C.
【解析】设点C的坐标为(m,/),则点E(/m,/),A(/m,/),
∵S△AEC=/BD?AE=/(/m﹣m)?(/﹣/)=﹣/k=/,∴k=﹣4.
二.填空题
7. 【答案】;
8. 【答案】(3,6);
【解析】由题意B点的坐标为(1,6),D点的坐标为(3,2),因为ABCD是矩形,故C点的坐标为(3,6).
9.【答案】9;
【解析】设y1=k1x,y2=/,则y=y1+y2=k1x+/,
将(1,2)、(2,/)代入得:/,
解得:/
∴8k1+5k2=/=9.
故答案为9.
10.【答案】-12;
【解析】由题意所以,因为,所以=-12.
11.【答案】105;
【解析】△AOB的面积始终为,故=.
12.【答案】;
【解析】()第一个阴影部分面积等于4;(),用待定系数法求出直线的解析式,再求出与的交点坐标为(),第二个阴影面积为=1;(),求出直线的解析式,再求出与的交点坐标为(),第三个阴影部分面积为,所以阴影部分面积之和为.
三.解答题
13.【解析】
解:(1)设反比例函数的解析式为y=/,
∵图象经过点P(2,﹣3),
∴k=2×(﹣3)=﹣6,
∴反比例函数的解析式为y=﹣/;
(2)∵点P沿x轴负方向平移3个单位,
∴点P′的横坐标为2﹣3=﹣1,
∴当x=﹣1时,y=﹣/=6,
∴∴n=6﹣(﹣3)=9,
∴沿着y轴平移的方向为正方向.
14.【解析】
解:(1)∵ D(-8,0),∴ B点的横坐标为-8,代入中,得=-2.
∴ B点坐标为(-8,-2).而A、B两点关于原点对称,∴ A(8,2) .
从而=8×2=16.
(2)∵ N(0,-),B是CD的中点,A、B、M、E四点均在双曲线上,
∴ ,,C(-2,-),E(-,-).
,,,
∴ .∴ =4.
由直线及双曲线,
得A(4,1),B(-4,-1),∴ C(-4,-2),M(2,2).
设直线CM的解析式是,由C、M两点在这条直线上,得
解得.
∴ 直线CM的解析式是.
15.【解析】
解:(1)∵B(3,﹣8)在反比例函数图象上,
∴﹣8=,m=﹣24,反比例函数的解析式为y=﹣/,
把A(﹣8,n)代入y=﹣/,n=3,
设一次函数解析式为y=kx+b,
/,
解得,/,
一次函数解析式为y=﹣x﹣5.
(2)﹣x﹣5=0,x=﹣5,
点C的坐标为(﹣5,0),
△AOB的面积=△AOC的面积+△BOC的面积=/×5×3+/×5×8=/.
(3)点A(﹣8,3),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数图象的两个交点,
方程kx+b﹣=0的解是:x1=﹣8,x2=3,
(4)由图象可知,当x<﹣8或0<x<3时,kx+b>,
∴不等式kx+b﹣>0的解集为:x<﹣8或0<x<3.
【学习目标】
1. 理解反比例函数的概念和意义,能根据问题的反比例关系确定函数解析式.
2. 能根据解析式画出反比例函数的图象,初步掌握反比例函数的图象和性质.
3. 会用待定系数法确定反比例函数解析式,进一步理解反比例函数的图象和性质.
4. 会解决一次函数和反比例函数有关的问题.
【巩固练习】
一.选择题
1. 在反比例函数/的图象上有两点A/,B/,当/时,有/,则/的取值范围是( )
A./ B./ C./ D./
2. 如图所示的图象上的函数关系式只能是( ) .
A. B. C. D.
/
3. 已知,点P()在反比例函数的图像上,则直线不经过的象限是( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 在函数(为常数)的图象上有三个点,,,则函数值、、的大小关系是( ).
A.<< B.<< C.<< D.<<
5. (2019?历下区模拟)如图,直线x=t(t>0)与反比例函数y=/(x>0)、y=/(x>0)的图象分别交于B、C两点,A为y轴上任意一点,△ABC的面积为3,则k的值为( )
/
A.2 B.3 C.4 D.5
6. (2019?本溪)如图,点A、C为反比例函数y=/图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为/时,k的值为( )
/
A.4 B.6 C.﹣4 D.﹣6
二.填空题
7. 如图所示是三个反比例函数、、的图象,由此观察得到、、的大小关系是____________________(用“<”连接).
/
8. 如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数(>0)的图象上,则点C的坐标为 _________ .
/
9. (2019春?江都市校级期末)已知y1与x成正比例(比例系数为k1),y2与x成反比例(比例系数为k2),若函数y=y1+y2的图象经过点(1,2),(2,/),则8k1+5k2的值为 .
10.已知A(),B()都在 图象上.若,则的值为 _________ .
11. 如图,正比例函数的图象与反比例函数(>0)的图象交于点A,若取1,2,3…20,对应的Rt△AOB的面积分别为,则
= ________.
/
12. 如图所示,点,,在x轴上,且,分别过点,, 作轴的平行线,与反比例函数=(>0)的图象分别交于点,,,分别过点,,作轴的平行线,分别于轴交于点,,,连接,,,那么图中阴影部分的面积之和为____________.
/
三.解答题
13. (2019?泉州)已知反比例函数的图象经过点P(2,﹣3).
(1)求该函数的解析式;
(2)若将点P沿x轴负方向平移3个单位,再沿y轴方向平移n(n>0)个单位得到点P′,使点P′恰好在该函数的图象上,求n的值和点P沿y轴平移的方向.
14. 如图所示,已知双曲线与直线相交于A、B两点.第一象限上的点M(,)(在A点左侧)是双曲线上的动点.过点B作BD∥轴交于x轴于点D.过N(0,-)作NC∥轴交双曲线于点E,交BD于点C.
/
(1)若点D坐标是(-8,0),求A、B两点坐标及的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
15. (2019春?耒阳市校级月考)如图,已知点A(﹣8,n),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积,
(3)求方程kx+b﹣=0的解(请直接写出答案);
(4)求不等式kx+b﹣>0的解集(请直接写出答案).
/
【答案与解析】
一.选择题
1.【答案】C;
【解析】由题意画出图象,只能在一、三象限,故.
2.【答案】D;
【解析】画出的图象,再把轴下方的图象翻折上去.
3.【答案】C;
【解析】由题意,故>0,直线经过一、二、四象限.
4.【答案】D;
【解析】,故图象在二、四象限,画出图象,比较大小得D答案.
5.【答案】D;
【解析】解:由题意得,点C的坐标(t,﹣/),点B的坐标(t,/),
BC=/+/,则/(/+/)×t=3,解得k=5,
故选:D.
6.【答案】C.
【解析】设点C的坐标为(m,/),则点E(/m,/),A(/m,/),
∵S△AEC=/BD?AE=/(/m﹣m)?(/﹣/)=﹣/k=/,∴k=﹣4.
二.填空题
7. 【答案】;
8. 【答案】(3,6);
【解析】由题意B点的坐标为(1,6),D点的坐标为(3,2),因为ABCD是矩形,故C点的坐标为(3,6).
9.【答案】9;
【解析】设y1=k1x,y2=/,则y=y1+y2=k1x+/,
将(1,2)、(2,/)代入得:/,
解得:/
∴8k1+5k2=/=9.
故答案为9.
10.【答案】-12;
【解析】由题意所以,因为,所以=-12.
11.【答案】105;
【解析】△AOB的面积始终为,故=.
12.【答案】;
【解析】()第一个阴影部分面积等于4;(),用待定系数法求出直线的解析式,再求出与的交点坐标为(),第二个阴影面积为=1;(),求出直线的解析式,再求出与的交点坐标为(),第三个阴影部分面积为,所以阴影部分面积之和为.
三.解答题
13.【解析】
解:(1)设反比例函数的解析式为y=/,
∵图象经过点P(2,﹣3),
∴k=2×(﹣3)=﹣6,
∴反比例函数的解析式为y=﹣/;
(2)∵点P沿x轴负方向平移3个单位,
∴点P′的横坐标为2﹣3=﹣1,
∴当x=﹣1时,y=﹣/=6,
∴∴n=6﹣(﹣3)=9,
∴沿着y轴平移的方向为正方向.
14.【解析】
解:(1)∵ D(-8,0),∴ B点的横坐标为-8,代入中,得=-2.
∴ B点坐标为(-8,-2).而A、B两点关于原点对称,∴ A(8,2) .
从而=8×2=16.
(2)∵ N(0,-),B是CD的中点,A、B、M、E四点均在双曲线上,
∴ ,,C(-2,-),E(-,-).
,,,
∴ .∴ =4.
由直线及双曲线,
得A(4,1),B(-4,-1),∴ C(-4,-2),M(2,2).
设直线CM的解析式是,由C、M两点在这条直线上,得
解得.
∴ 直线CM的解析式是.
15.【解析】
解:(1)∵B(3,﹣8)在反比例函数图象上,
∴﹣8=,m=﹣24,反比例函数的解析式为y=﹣/,
把A(﹣8,n)代入y=﹣/,n=3,
设一次函数解析式为y=kx+b,
/,
解得,/,
一次函数解析式为y=﹣x﹣5.
(2)﹣x﹣5=0,x=﹣5,
点C的坐标为(﹣5,0),
△AOB的面积=△AOC的面积+△BOC的面积=/×5×3+/×5×8=/.
(3)点A(﹣8,3),B(3,﹣8)是一次函数y=kx+b的图象和反比例函数图象的两个交点,
方程kx+b﹣=0的解是:x1=﹣8,x2=3,
(4)由图象可知,当x<﹣8或0<x<3时,kx+b>,
∴不等式kx+b﹣>0的解集为:x<﹣8或0<x<3.
