人教版九年级下数学教学讲义,复习补习资料(巩固练习):58【提高】相似三角形的判定含答案
文档属性
| 名称 | 人教版九年级下数学教学讲义,复习补习资料(巩固练习):58【提高】相似三角形的判定含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 94.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 00:00:00 | ||
图片预览

文档简介
相似三角形的判定--知识讲解(提高)
【学习目标】
1、了解相似三角形的概念, 掌握相似三角形的表示方法及判定方法;
2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.
相似三角形的判定--巩固练习(提高)
【巩固练习】
一、选择题
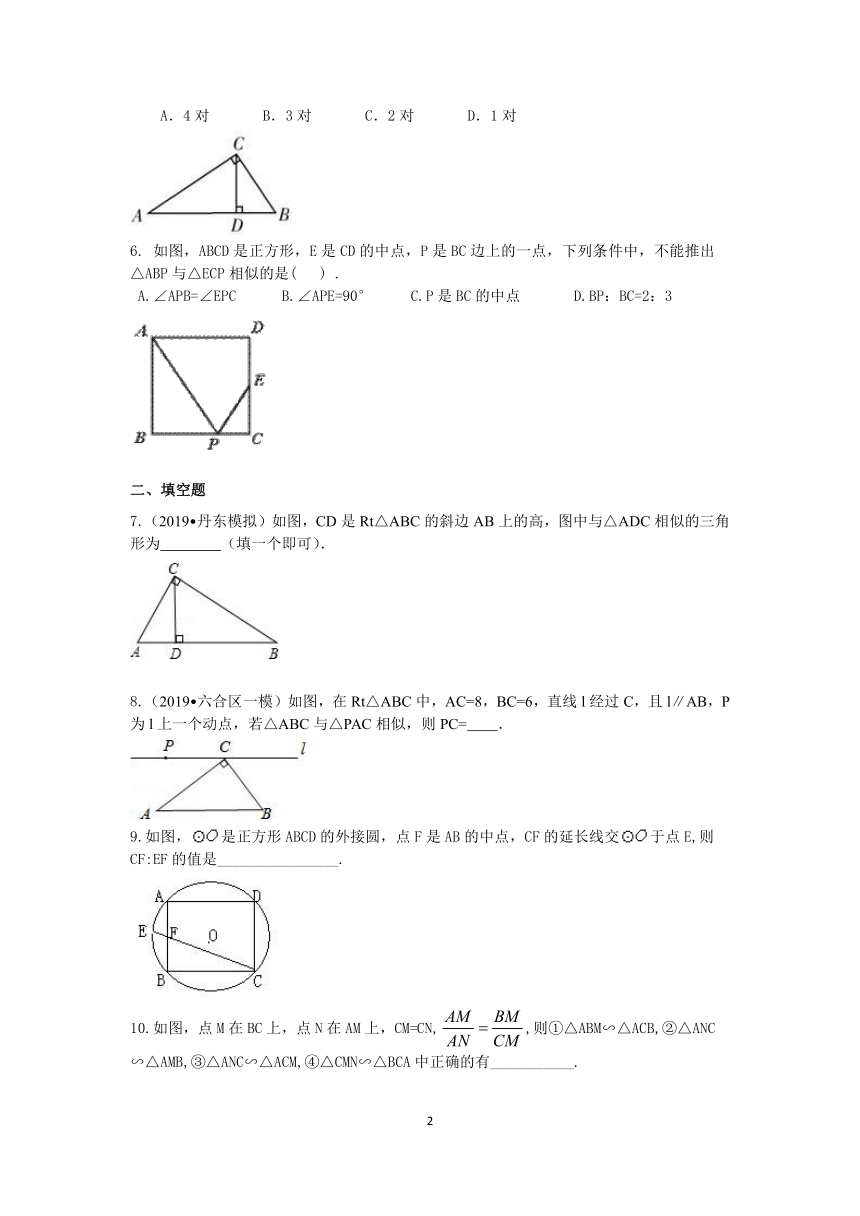
1. 已知△A1B1C1与△A2B2C2的相似比为4:3,△A2B2C2与△A3B3C3的相似比为4:5,则△A1B1C1与△A3B3C3的相似比为( ).
A.16:15 B.15:16 C.3:5 D.16:15或15:16 2.(2019?湘潭一模)如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连结EM并延长,交BC的延长线于D,此时BC:CD为( ) .
A. 2:1 B. 3:2 C. 3:1 D. 5:2
4.下列各组条件中,一定能推出△ABC与△DEF相似的是( )
A.∠A=∠E且∠D=∠F B.∠A=∠B且∠D=∠F
C.∠A=∠E且AB:AC=EF:ED D.∠A=∠E且AB:BC=DF:ED
5.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,则图中相似三角形有( ). A.4对 B.3对 C.2对 D.1对
6. 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( ) .
A.∠APB=∠EPC B.∠APE=90° C.P是BC的中点 D.BP:BC=2:3
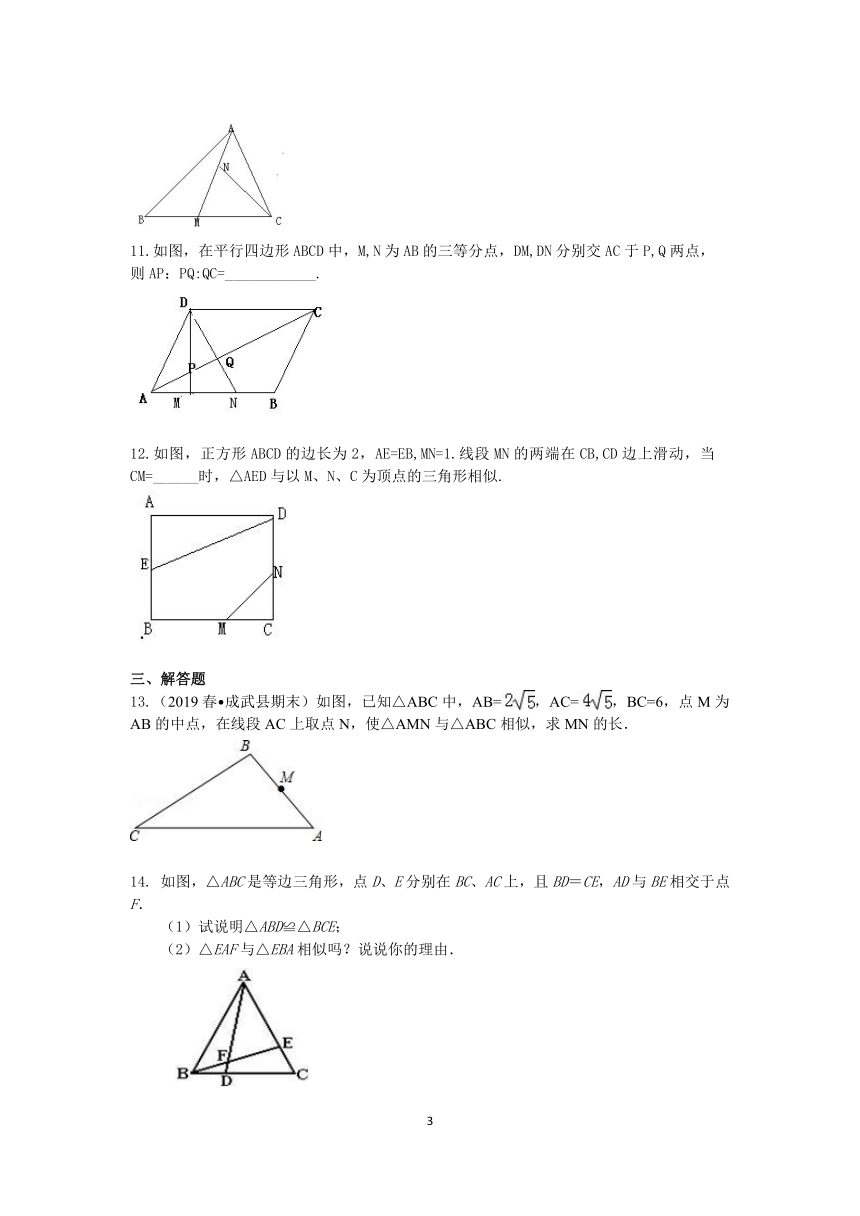
二、填空题 7.(2019?丹东模拟)如图,CD是Rt△ABC的斜边AB上的高,图中与△ADC相似的三角形为 (填一个即可).
8.(2019?六合区一模)如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC= .
9.如图,是正方形ABCD的外接圆,点F是AB的中点,CF的延长线交于点E,则CF:EF的值是________________.
10.如图,点M在BC上,点N在AM上,CM=CN,,则①△ABM∽△ACB,②△ANC∽△AMB,③△ANC∽△ACM,④△CMN∽△BCA中正确的有___________.
11.如图,在平行四边形ABCD中,M,N为AB的三等分点,DM,DN分别交AC于P,Q两点,则AP:PQ:QC=____________.
12.如图,正方形ABCD的边长为2,AE=EB,MN=1.线段MN的两端在CB,CD边上滑动,当CM=______时,△AED与以M、N、C为顶点的三角形相似.
三、解答题
13.(2019春?成武县期末)如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
14. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F. (1)试说明△ABD≌△BCE; (2)△EAF与△EBA相似吗?说说你的理由.
15.已知点P在线段AB上,点O在线段AB的延长线上.以点O为圆心,OP为半径作圆,点C是圆O上的一点. (1)如图,如果AP=2PB,PB=BO.求证:△CAO∽△BCO; (2)如果AP=m(m是常数,且),BP=1,OP是OA、OB的比例中项.当点C在圆O上运动时,求的值(结果用含m的式子表示); (3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应m的取值范围.
【答案与解析】
一.选择题
1.【答案】A.
2.【答案】B.
【解析】∵小正方形的边长均为1
∴△ABC三边分别为2,,
同理:A中各边的长分别为:,3,;
B中各边长分别为:,1,;
C中各边长分别为:1、2,;
D中各边长分别为:2,,;
∵只有B项中的三边与已知三角形的三边对应成比例,且相似比为
3.【答案】A .
【解析】如图,做CN∥AB,交ED于点N,
∵M是AC边中点,△AEM≌△CNM,即CN=AE,
∵AE=AB,∴AE:BE=1:3,即CN:BE=1:3.
∵CN∥AB,∴△DCN∽△DBE,即CD:BD= CN:BE=1:3,∴CD:BC=1:2.
4.【答案】C.
5.【答案】B.
【解析】△ABC∽△ACD; △ABC∽△CBD; △CBD∽△ACD.
6.【答案】C.
【解析】当P是BC的中点时,△EPC为等腰直角三角形.
二. 填空题
7.【答案】△ABC.
【解析】∵∠ACD+∠BCD=90°∠BCD+∠B=90°,
∴∠ACD=∠B,
∵∠A=∠A,
∴△ADC∽△ACB(AA).
8.【答案】10或6.4
9.【答案】5:1.
【解析】如图,连接AE,则△AEF∽△CBF,
∵点F是AB的中点,正方形ABCD,∴EF:AE=BF:BC=1:2.
设EF=K,则AE=2K,AF=K,即BF=K,BC=2K,CF=5K.
∴CF:EF=5:1.
10.【答案】②.
11.【答案】5:3:12.
【解析】∵平行四边形ABCD, M,N为AB的三等分点∴AM:CD=AP:PC=1:3,AN:CD=AQ:QC=2:3,
即AP=AC,AQ=AC,∴QP=AC,QC=AC,∴AP:PQ:QC=AC: AC: AC=5:3:12.
12.【答案】.
三 综合题
13.【解析】解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,
∴MN=3;
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,AC=,
∴MN=,
∴MN的长为3或.
14.【解析】(1)∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE=∠BAC, 又∵BD=CE,∴△ABD≌△BCE; (2)相似;∵△ABD≌△BCE,∴∠BAD=∠CBE, ∴∠BAC-∠BAD=∠CBA-∠CBE,∴∠EAF=∠EBA, 又∵∠AEF=∠BEA,∴△EAF∽△EBA.
15.【解析】(1)利用两边的比相等,夹角相等证相似. 由已知AP=2PB,PB=BO,
可推出
,,
∴△CAO∽△BCO.
(2)设, ∵是的比例中项, ∴是的比例中项. 即, ∴, 解得. 又∵?△COB∽△AOC, . (3)∵?,,即, 当?时,两圆内切;当?时,两圆内含;当?时,两圆相交.
【学习目标】
1、了解相似三角形的概念, 掌握相似三角形的表示方法及判定方法;
2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.
相似三角形的判定--巩固练习(提高)
【巩固练习】
一、选择题
1. 已知△A1B1C1与△A2B2C2的相似比为4:3,△A2B2C2与△A3B3C3的相似比为4:5,则△A1B1C1与△A3B3C3的相似比为( ).
A.16:15 B.15:16 C.3:5 D.16:15或15:16 2.(2019?湘潭一模)如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连结EM并延长,交BC的延长线于D,此时BC:CD为( ) .
A. 2:1 B. 3:2 C. 3:1 D. 5:2
4.下列各组条件中,一定能推出△ABC与△DEF相似的是( )
A.∠A=∠E且∠D=∠F B.∠A=∠B且∠D=∠F
C.∠A=∠E且AB:AC=EF:ED D.∠A=∠E且AB:BC=DF:ED
5.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,则图中相似三角形有( ). A.4对 B.3对 C.2对 D.1对
6. 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( ) .
A.∠APB=∠EPC B.∠APE=90° C.P是BC的中点 D.BP:BC=2:3
二、填空题 7.(2019?丹东模拟)如图,CD是Rt△ABC的斜边AB上的高,图中与△ADC相似的三角形为 (填一个即可).
8.(2019?六合区一模)如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC= .
9.如图,是正方形ABCD的外接圆,点F是AB的中点,CF的延长线交于点E,则CF:EF的值是________________.
10.如图,点M在BC上,点N在AM上,CM=CN,,则①△ABM∽△ACB,②△ANC∽△AMB,③△ANC∽△ACM,④△CMN∽△BCA中正确的有___________.
11.如图,在平行四边形ABCD中,M,N为AB的三等分点,DM,DN分别交AC于P,Q两点,则AP:PQ:QC=____________.
12.如图,正方形ABCD的边长为2,AE=EB,MN=1.线段MN的两端在CB,CD边上滑动,当CM=______时,△AED与以M、N、C为顶点的三角形相似.
三、解答题
13.(2019春?成武县期末)如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
14. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F. (1)试说明△ABD≌△BCE; (2)△EAF与△EBA相似吗?说说你的理由.
15.已知点P在线段AB上,点O在线段AB的延长线上.以点O为圆心,OP为半径作圆,点C是圆O上的一点. (1)如图,如果AP=2PB,PB=BO.求证:△CAO∽△BCO; (2)如果AP=m(m是常数,且),BP=1,OP是OA、OB的比例中项.当点C在圆O上运动时,求的值(结果用含m的式子表示); (3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应m的取值范围.
【答案与解析】
一.选择题
1.【答案】A.
2.【答案】B.
【解析】∵小正方形的边长均为1
∴△ABC三边分别为2,,
同理:A中各边的长分别为:,3,;
B中各边长分别为:,1,;
C中各边长分别为:1、2,;
D中各边长分别为:2,,;
∵只有B项中的三边与已知三角形的三边对应成比例,且相似比为
3.【答案】A .
【解析】如图,做CN∥AB,交ED于点N,
∵M是AC边中点,△AEM≌△CNM,即CN=AE,
∵AE=AB,∴AE:BE=1:3,即CN:BE=1:3.
∵CN∥AB,∴△DCN∽△DBE,即CD:BD= CN:BE=1:3,∴CD:BC=1:2.
4.【答案】C.
5.【答案】B.
【解析】△ABC∽△ACD; △ABC∽△CBD; △CBD∽△ACD.
6.【答案】C.
【解析】当P是BC的中点时,△EPC为等腰直角三角形.
二. 填空题
7.【答案】△ABC.
【解析】∵∠ACD+∠BCD=90°∠BCD+∠B=90°,
∴∠ACD=∠B,
∵∠A=∠A,
∴△ADC∽△ACB(AA).
8.【答案】10或6.4
9.【答案】5:1.
【解析】如图,连接AE,则△AEF∽△CBF,
∵点F是AB的中点,正方形ABCD,∴EF:AE=BF:BC=1:2.
设EF=K,则AE=2K,AF=K,即BF=K,BC=2K,CF=5K.
∴CF:EF=5:1.
10.【答案】②.
11.【答案】5:3:12.
【解析】∵平行四边形ABCD, M,N为AB的三等分点∴AM:CD=AP:PC=1:3,AN:CD=AQ:QC=2:3,
即AP=AC,AQ=AC,∴QP=AC,QC=AC,∴AP:PQ:QC=AC: AC: AC=5:3:12.
12.【答案】.
三 综合题
13.【解析】解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,
∴MN=3;
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,AC=,
∴MN=,
∴MN的长为3或.
14.【解析】(1)∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE=∠BAC, 又∵BD=CE,∴△ABD≌△BCE; (2)相似;∵△ABD≌△BCE,∴∠BAD=∠CBE, ∴∠BAC-∠BAD=∠CBA-∠CBE,∴∠EAF=∠EBA, 又∵∠AEF=∠BEA,∴△EAF∽△EBA.
15.【解析】(1)利用两边的比相等,夹角相等证相似. 由已知AP=2PB,PB=BO,
可推出
,,
∴△CAO∽△BCO.
(2)设, ∵是的比例中项, ∴是的比例中项. 即, ∴, 解得. 又∵?△COB∽△AOC, . (3)∵?,,即, 当?时,两圆内切;当?时,两圆内含;当?时,两圆相交.
