人教版九年级下数学教学讲义,复习补习资料(巩固练习):60【提高】相似三角形的性质及应用含答案
文档属性
| 名称 | 人教版九年级下数学教学讲义,复习补习资料(巩固练习):60【提高】相似三角形的性质及应用含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 15:50:14 | ||
图片预览

文档简介
相似三角形的性质及应用--知识讲解(提高)
【学习目标】
1、探索相似三角形的性质,能运用性质进行有关计算;
2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题).
相似三角形的性质及应用--巩固练习(提高)
【巩固练习】
一、选择题
1.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个 B.可以有2个 C.有2个以上,但有限 D.有无数个
2. 若平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为( ).
A.1.8 B.5 C.6或4 D.8或2
3. (2019?兰州)已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
4.如图G是△ABC的重心,直线过A点与BC平行.若直线CG分别与AB、交于D、E两点,直线BG与AC交于 F点,则△AED的面积 :四边形ADGF的面积=( )? A.1:2 B.2:1 C.2:3 D.3:2 5.(2019?哈尔滨)如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B. = C. = D.=
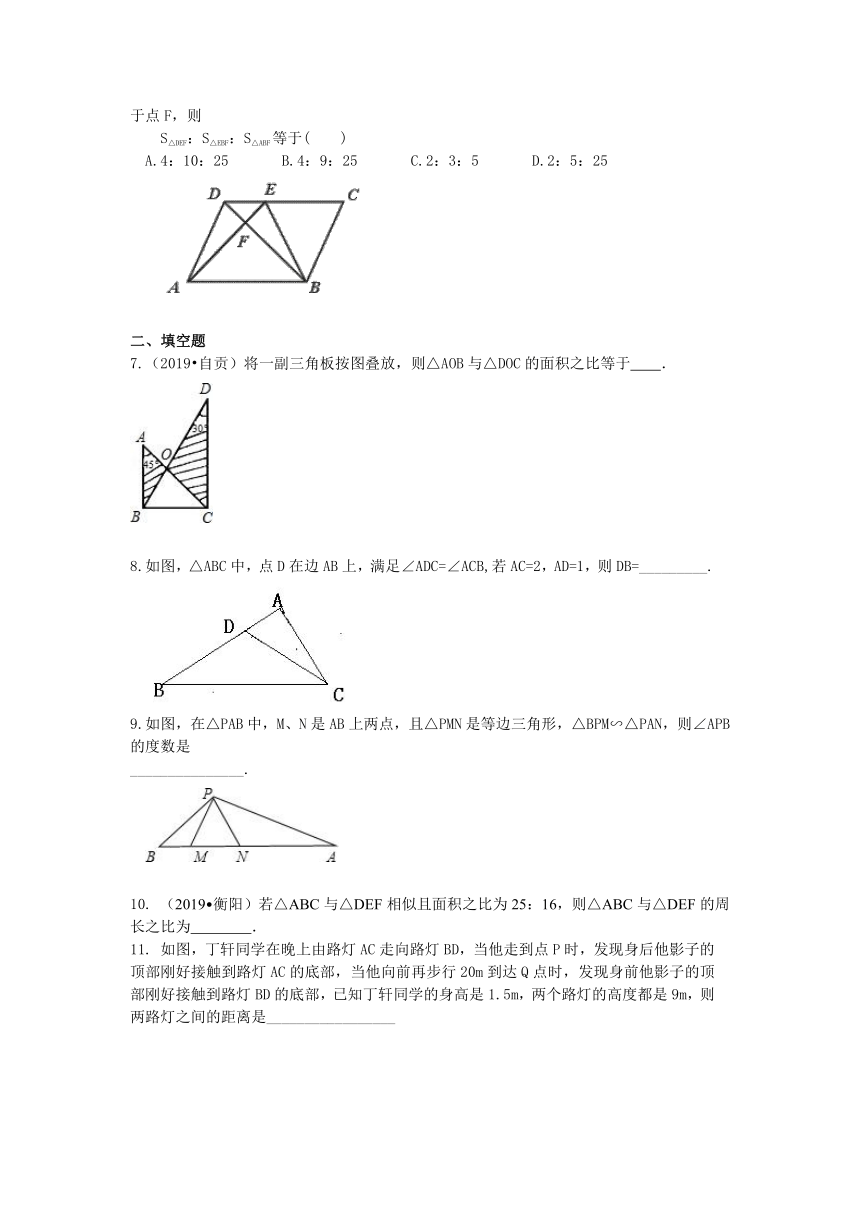
6.如图,在□ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD,且AE、BD交于点F,则 S△DEF:S△EBF:S△ABF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
二、填空题
7.(2019?自贡)将一副三角板按图叠放,则△AOB与△DOC的面积之比等于 .
8.如图,△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB=_________.
9.如图,在△PAB中,M、N是AB上两点,且△PMN是等边三角形,△BPM∽△PAN,则∠APB的度数是
_______________.
10. (2019?衡阳)若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
11. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是_________________
12.如图,锐角△ABC中,AD,CE分别为BC,AB边上的高,△ABC和△BDE的面积分别等于18和2,DE=2,
则AC边上的高为______________.
三、解答题
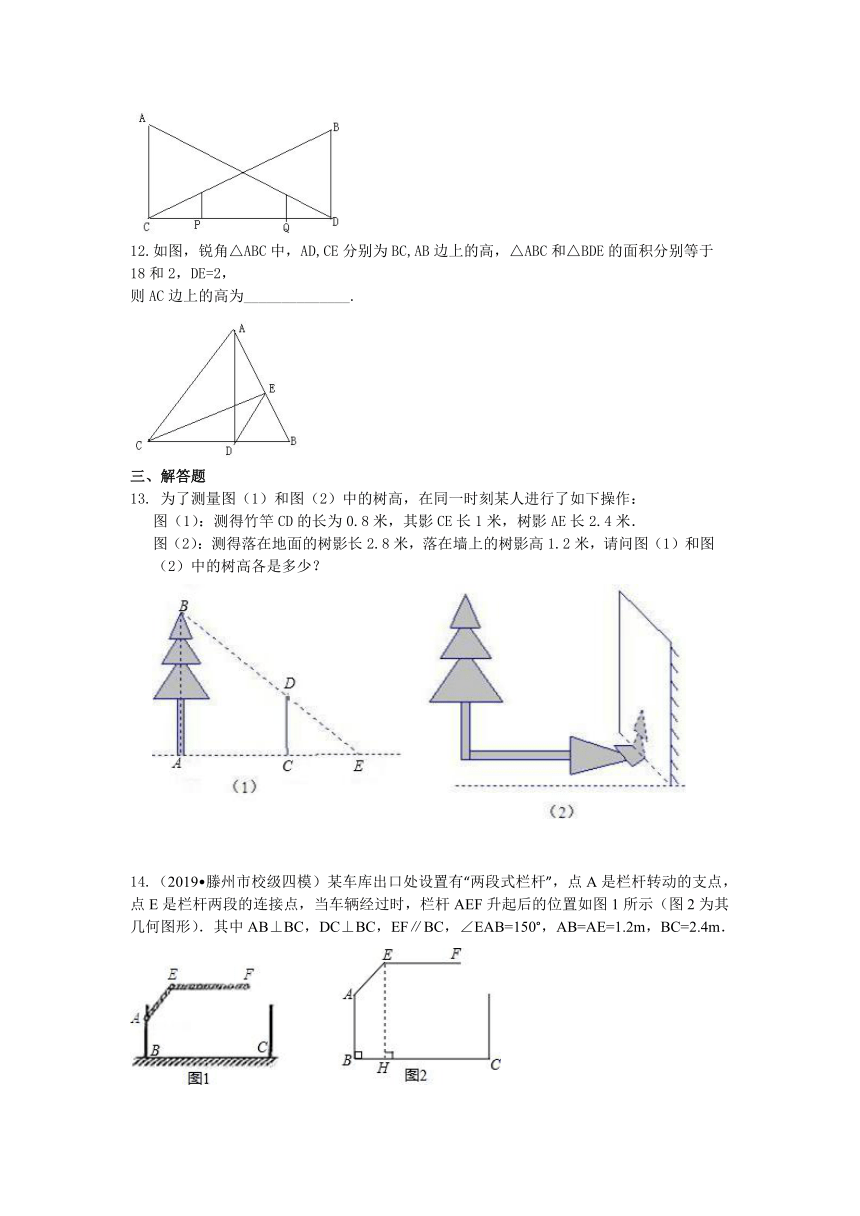
13. 为了测量图(1)和图(2)中的树高,在同一时刻某人进行了如下操作: 图(1):测得竹竿CD的长为0.8米,其影CE长1米,树影AE长2.4米. 图(2):测得落在地面的树影长2.8米,落在墙上的树影高1.2米,请问图(1)和图(2)中的树高各是多少?
14.(2019?滕州市校级四模)某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.
(1)求图2中点E到地面的高度(即EH的长.≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由.
15. 已知如图,在矩形ABCD中,AB=12cm,BC=6cm,点E自A点出发,以每秒1cm的速度向D点前进,同时点F从D点以每秒2cm的速度向C点前进,若移动的时间为t,且0≤t≤6. (1)当t为多少时,DE=2DF; (2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由. (3)以点D、E、F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.
【答案与解析】
一.选择题
1.【答案】B.
【解析】x可能是斜边,也可能是直角边.
2.【答案】A.
3.【答案】A.
【解析】∵△ABC∽△DEF,△ABC与△DEF的相似比为,∴△ABC与△DEF对应中线的比为.
4.【答案】D.
5.【答案】C.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BF,BE∥DC,AD=BC,
∴,,,
故选C.
6.【答案】 A.
【解析】 □ABCD中,AB∥DC,△DEF∽△ABF, (△DEF与△EBF等高,面积比等于对应底边的比),所以答案选A.
二、填空题
7.【答案】1:3.
【解析】∵∠ABC=90°,∠DCB=90°
∴AB∥CD,∴∠OCD=∠A,∠D=∠ABO,
∴△AOB∽△COD;又∵AB:CD=BC:CD= 1:
∴△AOB与△DOC的面积之比等于1:3.
8.【答案】3.
【解析】 ∵∠ADC=∠ACB,∠DAC=∠BAC,∴△ACD∽△ABC,∴AB=
∴BD=AB-AD=4-1=3.
9. 【答案】120°.
【解析】∵ △BPM∽△PAN,∴ ∠BPM=∠A,
∵ △PMN是等边三角形,∴ ∠A+∠APN=60°,即∠APN+∠BPM=60°,
∴ ∠APB=∠BPM+∠MPN+∠APN=60°+60°=120°.
10.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,
∴△ABC与△DEF的相似比为5:4;
∴△ABC与△DEF的周长之比为5:4.
11.【答案】30m.
12.【答案】 6.
【解析】∵AD,CE分别为BC,AB边上的高,
∴∠ADB=∠BEC=90°,∠ABD=∠EBC
∴Rt△ABD∽Rt△CBE
∴,
∴△ABC∽△DBE
∵相似三角形面积比为相似比的平方,
∴= 9, ∴=3 ,
∴AC=3DE=3×2=6
∴h=2S△ABC/AC=2×18/6=6
即AC边上的高是6 .
三、解答题 13.【解析】(1)∵△CDE∽△ABE,∴, 又竹竿CD的长为0.8米,其影CE长1米,树影AE长2.4米, ∴ AB=1.92米.即图1的树高为1.92米. (2)设墙上的影高落在地面上时的长度为x,树高为h, ∵竹竿CD的长为0.8米,其影CE长1米, ∴
解得x=1.5(m), ∴树的影长为:1.5+2.8=4.3(m), ∴
解得h=3.44(m). 14.【解析】解:(1)如图,作AM⊥EH于点M,交CD于点N,
则四边形ABHM和MHCN都是矩形,
∵∠EAB=150°,∴∠EAM=60°,
又∵AB=AE=1.2米,
∴EM=0.6≈0.6×1.73=1.038≈1.04(米),
∴EH≈2.24(米);
(2)如图,在AE上取一点P,过点P分别作BC,CD的垂线,垂足分别是Q,R,PR交EH于点K,不妨设PQ=2米,
下面计算PR是否小于2米;
由上述条件可得EK=EH﹣PQ=0.24米,AM=0.6米,
∵PK∥AM,∴△EPK∽△EAM,
∴=,即=,
∴PK=0.08(米),
∴PR=PK+MN=PK+BC﹣AM=0.08+2.4﹣0.6
=1.8+0.08
≈1.94(米),
∵PR<2米,∴这辆车不能驶入该车库.
15.【解析】(1)由题意得:DE=AD-t=6-t,DF=2t, ∴6-t=2×2t,解得t=, 故当t=时,DE=2DF;
(2)∵矩形ABCD的面积为:12×6=72,S△ABE=×12×t=6t,
S△BCF=×6×(12-2t)=36-6t,
∴四边形DEBF的面积=矩形的面积-S△ABE-S△BCF=72-6t-36+6t=36,
故四边形DEBF的面积为定值.
(3)设以点D、E、F为顶点的三角形能与△BCD相似,
则或, 由ED=6-t,DF=2t,FC=12-2t,BC=6,
代入解得:t=3或t=1.2, 故当t=3或1.2时,以点D、E、F为顶点的三角形与△BCD相似.
【学习目标】
1、探索相似三角形的性质,能运用性质进行有关计算;
2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题).
相似三角形的性质及应用--巩固练习(提高)
【巩固练习】
一、选择题
1.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个 B.可以有2个 C.有2个以上,但有限 D.有无数个
2. 若平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为( ).
A.1.8 B.5 C.6或4 D.8或2
3. (2019?兰州)已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
4.如图G是△ABC的重心,直线过A点与BC平行.若直线CG分别与AB、交于D、E两点,直线BG与AC交于 F点,则△AED的面积 :四边形ADGF的面积=( )? A.1:2 B.2:1 C.2:3 D.3:2 5.(2019?哈尔滨)如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B. = C. = D.=
6.如图,在□ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD,且AE、BD交于点F,则 S△DEF:S△EBF:S△ABF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
二、填空题
7.(2019?自贡)将一副三角板按图叠放,则△AOB与△DOC的面积之比等于 .
8.如图,△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB=_________.
9.如图,在△PAB中,M、N是AB上两点,且△PMN是等边三角形,△BPM∽△PAN,则∠APB的度数是
_______________.
10. (2019?衡阳)若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
11. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是_________________
12.如图,锐角△ABC中,AD,CE分别为BC,AB边上的高,△ABC和△BDE的面积分别等于18和2,DE=2,
则AC边上的高为______________.
三、解答题
13. 为了测量图(1)和图(2)中的树高,在同一时刻某人进行了如下操作: 图(1):测得竹竿CD的长为0.8米,其影CE长1米,树影AE长2.4米. 图(2):测得落在地面的树影长2.8米,落在墙上的树影高1.2米,请问图(1)和图(2)中的树高各是多少?
14.(2019?滕州市校级四模)某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.
(1)求图2中点E到地面的高度(即EH的长.≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由.
15. 已知如图,在矩形ABCD中,AB=12cm,BC=6cm,点E自A点出发,以每秒1cm的速度向D点前进,同时点F从D点以每秒2cm的速度向C点前进,若移动的时间为t,且0≤t≤6. (1)当t为多少时,DE=2DF; (2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由. (3)以点D、E、F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.
【答案与解析】
一.选择题
1.【答案】B.
【解析】x可能是斜边,也可能是直角边.
2.【答案】A.
3.【答案】A.
【解析】∵△ABC∽△DEF,△ABC与△DEF的相似比为,∴△ABC与△DEF对应中线的比为.
4.【答案】D.
5.【答案】C.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BF,BE∥DC,AD=BC,
∴,,,
故选C.
6.【答案】 A.
【解析】 □ABCD中,AB∥DC,△DEF∽△ABF, (△DEF与△EBF等高,面积比等于对应底边的比),所以答案选A.
二、填空题
7.【答案】1:3.
【解析】∵∠ABC=90°,∠DCB=90°
∴AB∥CD,∴∠OCD=∠A,∠D=∠ABO,
∴△AOB∽△COD;又∵AB:CD=BC:CD= 1:
∴△AOB与△DOC的面积之比等于1:3.
8.【答案】3.
【解析】 ∵∠ADC=∠ACB,∠DAC=∠BAC,∴△ACD∽△ABC,∴AB=
∴BD=AB-AD=4-1=3.
9. 【答案】120°.
【解析】∵ △BPM∽△PAN,∴ ∠BPM=∠A,
∵ △PMN是等边三角形,∴ ∠A+∠APN=60°,即∠APN+∠BPM=60°,
∴ ∠APB=∠BPM+∠MPN+∠APN=60°+60°=120°.
10.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,
∴△ABC与△DEF的相似比为5:4;
∴△ABC与△DEF的周长之比为5:4.
11.【答案】30m.
12.【答案】 6.
【解析】∵AD,CE分别为BC,AB边上的高,
∴∠ADB=∠BEC=90°,∠ABD=∠EBC
∴Rt△ABD∽Rt△CBE
∴,
∴△ABC∽△DBE
∵相似三角形面积比为相似比的平方,
∴= 9, ∴=3 ,
∴AC=3DE=3×2=6
∴h=2S△ABC/AC=2×18/6=6
即AC边上的高是6 .
三、解答题 13.【解析】(1)∵△CDE∽△ABE,∴, 又竹竿CD的长为0.8米,其影CE长1米,树影AE长2.4米, ∴ AB=1.92米.即图1的树高为1.92米. (2)设墙上的影高落在地面上时的长度为x,树高为h, ∵竹竿CD的长为0.8米,其影CE长1米, ∴
解得x=1.5(m), ∴树的影长为:1.5+2.8=4.3(m), ∴
解得h=3.44(m). 14.【解析】解:(1)如图,作AM⊥EH于点M,交CD于点N,
则四边形ABHM和MHCN都是矩形,
∵∠EAB=150°,∴∠EAM=60°,
又∵AB=AE=1.2米,
∴EM=0.6≈0.6×1.73=1.038≈1.04(米),
∴EH≈2.24(米);
(2)如图,在AE上取一点P,过点P分别作BC,CD的垂线,垂足分别是Q,R,PR交EH于点K,不妨设PQ=2米,
下面计算PR是否小于2米;
由上述条件可得EK=EH﹣PQ=0.24米,AM=0.6米,
∵PK∥AM,∴△EPK∽△EAM,
∴=,即=,
∴PK=0.08(米),
∴PR=PK+MN=PK+BC﹣AM=0.08+2.4﹣0.6
=1.8+0.08
≈1.94(米),
∵PR<2米,∴这辆车不能驶入该车库.
15.【解析】(1)由题意得:DE=AD-t=6-t,DF=2t, ∴6-t=2×2t,解得t=, 故当t=时,DE=2DF;
(2)∵矩形ABCD的面积为:12×6=72,S△ABE=×12×t=6t,
S△BCF=×6×(12-2t)=36-6t,
∴四边形DEBF的面积=矩形的面积-S△ABE-S△BCF=72-6t-36+6t=36,
故四边形DEBF的面积为定值.
(3)设以点D、E、F为顶点的三角形能与△BCD相似,
则或, 由ED=6-t,DF=2t,FC=12-2t,BC=6,
代入解得:t=3或t=1.2, 故当t=3或1.2时,以点D、E、F为顶点的三角形与△BCD相似.
