江苏省南京市两校联考2020届高三12月月考数学(理)试题 Word版
文档属性
| 名称 | 江苏省南京市两校联考2020届高三12月月考数学(理)试题 Word版 |  | |
| 格式 | zip | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 09:28:39 | ||
图片预览




文档简介
2020届高三第一学期
第二次阶段
数学(理)考试
2019.12.11
考试时间:120分钟
满分:160分
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.设集合,则
▲
.
.
2.已知复数满足,其中为虚数单位,则的模为▲
.
3.函数的定义域为
▲
.
4.已知,则=
▲
.
5.若轴是曲线的一条切线,则
▲
.
6.已知双曲线的右焦点为若以为圆心的圆与此双曲线的渐近线相切,则该双曲线的离心率为
▲
.
7.已知函数,则不等式的解集为
_▲
.
8.如图,在扇形中,,,为弧上的一点,与相交于点,若,则的值为_
▲
.
9.
已知是公差不为0的等差数列,是其前项和.若,,则的值是
▲
.
10.在中,角的对边分别为,
若
,
,则
▲
.
11.若为半圆直径延长线上的一点,且,过动点作半圆的切线,切点为,若,则面积的最大值为_▲
.
12.已知椭圆,椭圆内接平行四边形的一组对边分别经过它的两个焦点,则这个平行四边形面积的最大值为
▲
.
13.若实数满足,则的最大值为__▲
.
14.已知函数
,若方程有6个实数根(互不相同),则实数的取值范围是__▲
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
在△ABC中,角A,B,C所对应的边分别是a,b,c,向量m=(a-c,b+c),n=(b-c,a),且m∥n.
(1)
求B;(2)
若b=,cos=,求a.
16.(本小题满分14分)
如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.
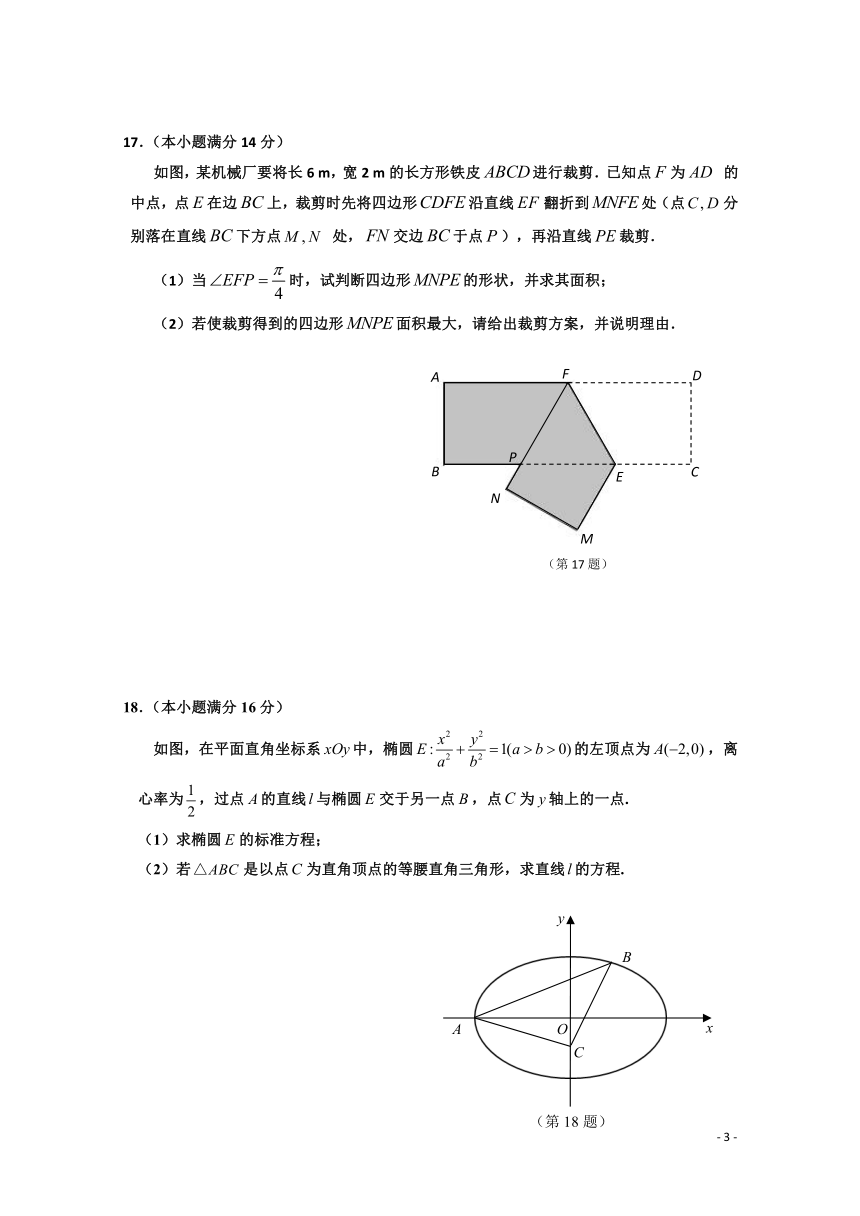
17.(本小题满分14分)
如图,某机械厂要将长6
m,宽2
m的长方形铁皮进行裁剪.已知点为
的中点,点在边上,裁剪时先将四边形沿直线翻折到处(点分别落在直线下方点
处,交边于点),再沿直线裁剪.
(1)当时,试判断四边形的形状,并求其面积;
(2)若使裁剪得到的四边形面积最大,请给出裁剪方案,并说明理由.
18.(本小题满分16分)
如图,在平面直角坐标系中,椭圆的左顶点为,离心率为,过点的直线与椭圆交于另一点,点为轴上的一点.
(1)求椭圆的标准方程;
(2)若是以点为直角顶点的等腰直角三角形,求直线的方程.
19.
(本小题满分16分)
已知函数(),是自然对数的底数.
(1)当时,求的定义域及单调增区间;
(2)若对任意的,(),求的最大值;
(3)若的极大值为,求不等式的解集.
20.(本小题满分16分)
已知数列,满足:对于任意正整数n,当n≥2时,.
(1)若,求的值;
(2)若,,且数列的各项均为正数.
①
求数列的通项公式;
②
是否存在,且,使得为数列中的项?
若存在,求出所有满足条件的的值;若不存在,请说明理由.
数学附加题
(本部分满分40分,考试时间30分钟)
21.
(本小题满分10分)
已知矩阵A=
的一个特征值为2,其对应的一个特征向量为a=
,求实数a,b的值.
22.
(本小题满分10分)
在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.直线
l:ρsin(θ一)=m(m∈R),圆C的参数方程为(t为参数).当圆心C到直线l的距离为时,求m的值。
23.
(本小题满分10分)
在直三棱柱ABCA1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1)
求直线DC1与平面A1B1D所成角的正弦值;
(2)
求二面角B1DC1A1的余弦值.
24.
(本小题满分10分)
已知x,y为整数,且x>y>0,θ∈,n为正整数,cos
θ=,sin
θ=,记An=(x2+y2)ncos
nθ,Bn=(x2+y2)nsin
nθ.
(1)
试用x,y分别表示A1,B1;
(2)
用数学归纳法证明:对一切正整数n,An均为整数.
参考答案
一、填空题:
1.
.2.
3.
4.
5.
6.
7.
.
8.4
9.
10.
4
11.
;
12.
4
13.
14.
二、解答题:
15.在△ABC中,角A,B,C所对应的边分别是a,b,c,向量m=(a-c,b+c),n=(b-c,a),且m∥n.
(1)
求B;
(2)
若b=,cos=,求a.
解:(1)
因为m∥n,所以a2+c2-b2=ac,(2分)
因为cosB===,(4分)
B∈(0,π)(5分)
故B=.(6分)
(2)
因为A+∈,(7分)
cos=,所以sin=,(9分)
所以sinA=sin=,(11分)
在△ABC中,由正弦定理可得:=,(13分)
解得a=1.(14分)
17.【解】(1)当∠EFP=时,由条件得
∠EFP=∠EFD=∠FEP=.
所以∠FPE=.所以FN⊥BC,四边形MNPE为矩形.……
3分
所以四边形MNPE的面积=2
m2.………
5分
(2)解法一:设,由条件,已知∠EFP=∠EFD=∠FEP=.
所以,
,
.
……………8分
由得
所以四边形MNPE面积为
……2分
.
当且仅当,即时取“=”.……13分
此时,成立.
答:当时,沿直线PE裁剪,四边形MNPE面积最大,
最大值为
m2.
……………………………………14分
18.(1).··········4分
(2)设直线的方程为,代入,
得,
因为为该方程的一个根,解得,··············6分
设,由,得:,
即:
··················10分
由,即,得,
即,
即,所以或,·····13分
当时,直线的方程为,
当时,代入得,解得,此时直线的方程为.
综上,直线的方程为,.
·························16分
19.
【解】(1)的定义域为.
……
2分
由,
令,因为,得,因为,
所以的单调增区间是.
……
4分
(2)当时,,不合题意;
当时,令,得或,
所以在区间和上单调递减.
因为,且在区间上单调递增,
所以在处取极小值,即最小值为.
……
6分
若,,则,即.
不妨设,则.
……
8分
设(),则.
当时,;当时,,
所以在上单调递增;在上单调递减,
所以,即,
所以的最大值为.……
10分
(3)由(2)知,当时,无极大值,
当时,在和上单调递增;在上单调递减,
所以在处取极大值,
所以,即.
……
12分
设,即,
当,,所以;
当,,
由(2)知,,又,
所以,且不恒为零,
所以在上单调递增.
不等式,即为,所以,
即不等式的解集为.
……
16分
20.(1)由条件,,,,,
,,所以.
(2)①由,
,,,…,.
将上面的式子相加,得,
所以.
因为{an}的各项均为正数,故.
因为也适合上式,所以().
②
假设存在满足条件的k
,不妨设,
所以,
平方得,(
)
所以,
所以,
即
由(1)得,,即,
若,代入(
)式,求得不合,舍去;
若,结合(2)得,
所以,即,又且,
所以的可能取值为2,3,4,代入(
)式逐一计算,可求得.
21..由条件知,,即,即,……………6分
所以
解得
所以,的值分别为,.……………………………………………………10分
22.直线的直角坐标方程为,
圆的普通方程为,…………………………………………5分
圆心到直线的距离,解得或.…………10分
23.
(1)
在直三棱柱ABCA1B1C1中,有AB⊥AC,AA1⊥AB,AA1⊥AC,
故可以{,,}为正交基底,建立如图所示的空间直角坐标系.(1分)
因为AB=2,AC=4,AA1=3,
所以A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3).
因为D是BC的中点,所以D(1,2,0).
所以=(-1,2,3).
设n1=(x1,y1,z1)为平面A1B1D的法向量,
因为=(2,0,0),=(-1,2,-3),
所以即
令y1=3,则x1=0,z1=2,所以平面A1B1D的一个法向量为n1=(0,3,2).(3分)
设直线DC1与平面A1B1D所成的角为θ,
则sin
θ=|cos?,n1?|==,
所以直线DC1与平面A1B1D所成角的正弦值为.(5分)
(2)
由(1)知=(-1,2,3),=(-2,4,0),
设n2=(x2,y2,z2)为平面B1DC1的法向量,
则即
令x2=2,则y2=1,z2=0,所以平面B1DC1的一个法向量为n2=(2,1,0).(7分)
同理可以求得平面A1DC1的一个法向量n3=(3,0,1),
所以cos?n2,n3?==,(9分)
由图可知二面角B1DC1A1的余弦值为.(10分)
24.
(1)
A1=(x2+y2)cos
θ=(x2+y2)·=x2-y2,(1分)
B1=(x2+y2)sin
θ=(x2+y2)·=2xy.(2分)
(2)
①当n=1时,由(1)得A1=x2-y2,B1=2xy.
因为x,y为整数,
所以A1,B1均为整数,所以结论成立;(4分)
②当n=k(k≥2,k∈N
)时,假设Ak,Bk均为整数,
则当n=k+1时,Ak+1=(x2+y2)k+1cos
(k+1)θ
=(x2+y2)(x2+y2)k(cos
kθcos
θ-sin
kθsin
θ)
=(x2+y2)cos
θ·(x2+y2)kcos
kθ-(x2+y2)ksin
kθ·(x2+y2)sin
θ
=A1·Ak-B1·Bk.(9分)
因为A1,B1,均为整数,所以Ak+1也为整数,
即当n=k+1时,结论也成立.
综合①②得,对一切正整数n,An均为整数.(10分)
A
B
C
D
F
E
P
M
N
(第17题)
y
O
A
B
C
x
(第18题)
A
B
C
D
F
E
P
M
N
(第18题)
PAGE
-
2
-
第二次阶段
数学(理)考试
2019.12.11
考试时间:120分钟
满分:160分
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.设集合,则
▲
.
.
2.已知复数满足,其中为虚数单位,则的模为▲
.
3.函数的定义域为
▲
.
4.已知,则=
▲
.
5.若轴是曲线的一条切线,则
▲
.
6.已知双曲线的右焦点为若以为圆心的圆与此双曲线的渐近线相切,则该双曲线的离心率为
▲
.
7.已知函数,则不等式的解集为
_▲
.
8.如图,在扇形中,,,为弧上的一点,与相交于点,若,则的值为_
▲
.
9.
已知是公差不为0的等差数列,是其前项和.若,,则的值是
▲
.
10.在中,角的对边分别为,
若
,
,则
▲
.
11.若为半圆直径延长线上的一点,且,过动点作半圆的切线,切点为,若,则面积的最大值为_▲
.
12.已知椭圆,椭圆内接平行四边形的一组对边分别经过它的两个焦点,则这个平行四边形面积的最大值为
▲
.
13.若实数满足,则的最大值为__▲
.
14.已知函数
,若方程有6个实数根(互不相同),则实数的取值范围是__▲
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
在△ABC中,角A,B,C所对应的边分别是a,b,c,向量m=(a-c,b+c),n=(b-c,a),且m∥n.
(1)
求B;(2)
若b=,cos=,求a.
16.(本小题满分14分)
如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.
17.(本小题满分14分)
如图,某机械厂要将长6
m,宽2
m的长方形铁皮进行裁剪.已知点为
的中点,点在边上,裁剪时先将四边形沿直线翻折到处(点分别落在直线下方点
处,交边于点),再沿直线裁剪.
(1)当时,试判断四边形的形状,并求其面积;
(2)若使裁剪得到的四边形面积最大,请给出裁剪方案,并说明理由.
18.(本小题满分16分)
如图,在平面直角坐标系中,椭圆的左顶点为,离心率为,过点的直线与椭圆交于另一点,点为轴上的一点.
(1)求椭圆的标准方程;
(2)若是以点为直角顶点的等腰直角三角形,求直线的方程.
19.
(本小题满分16分)
已知函数(),是自然对数的底数.
(1)当时,求的定义域及单调增区间;
(2)若对任意的,(),求的最大值;
(3)若的极大值为,求不等式的解集.
20.(本小题满分16分)
已知数列,满足:对于任意正整数n,当n≥2时,.
(1)若,求的值;
(2)若,,且数列的各项均为正数.
①
求数列的通项公式;
②
是否存在,且,使得为数列中的项?
若存在,求出所有满足条件的的值;若不存在,请说明理由.
数学附加题
(本部分满分40分,考试时间30分钟)
21.
(本小题满分10分)
已知矩阵A=
的一个特征值为2,其对应的一个特征向量为a=
,求实数a,b的值.
22.
(本小题满分10分)
在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.直线
l:ρsin(θ一)=m(m∈R),圆C的参数方程为(t为参数).当圆心C到直线l的距离为时,求m的值。
23.
(本小题满分10分)
在直三棱柱ABCA1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1)
求直线DC1与平面A1B1D所成角的正弦值;
(2)
求二面角B1DC1A1的余弦值.
24.
(本小题满分10分)
已知x,y为整数,且x>y>0,θ∈,n为正整数,cos
θ=,sin
θ=,记An=(x2+y2)ncos
nθ,Bn=(x2+y2)nsin
nθ.
(1)
试用x,y分别表示A1,B1;
(2)
用数学归纳法证明:对一切正整数n,An均为整数.
参考答案
一、填空题:
1.
.2.
3.
4.
5.
6.
7.
.
8.4
9.
10.
4
11.
;
12.
4
13.
14.
二、解答题:
15.在△ABC中,角A,B,C所对应的边分别是a,b,c,向量m=(a-c,b+c),n=(b-c,a),且m∥n.
(1)
求B;
(2)
若b=,cos=,求a.
解:(1)
因为m∥n,所以a2+c2-b2=ac,(2分)
因为cosB===,(4分)
B∈(0,π)(5分)
故B=.(6分)
(2)
因为A+∈,(7分)
cos=,所以sin=,(9分)
所以sinA=sin=,(11分)
在△ABC中,由正弦定理可得:=,(13分)
解得a=1.(14分)
17.【解】(1)当∠EFP=时,由条件得
∠EFP=∠EFD=∠FEP=.
所以∠FPE=.所以FN⊥BC,四边形MNPE为矩形.……
3分
所以四边形MNPE的面积=2
m2.………
5分
(2)解法一:设,由条件,已知∠EFP=∠EFD=∠FEP=.
所以,
,
.
……………8分
由得
所以四边形MNPE面积为
……2分
.
当且仅当,即时取“=”.……13分
此时,成立.
答:当时,沿直线PE裁剪,四边形MNPE面积最大,
最大值为
m2.
……………………………………14分
18.(1).··········4分
(2)设直线的方程为,代入,
得,
因为为该方程的一个根,解得,··············6分
设,由,得:,
即:
··················10分
由,即,得,
即,
即,所以或,·····13分
当时,直线的方程为,
当时,代入得,解得,此时直线的方程为.
综上,直线的方程为,.
·························16分
19.
【解】(1)的定义域为.
……
2分
由,
令,因为,得,因为,
所以的单调增区间是.
……
4分
(2)当时,,不合题意;
当时,令,得或,
所以在区间和上单调递减.
因为,且在区间上单调递增,
所以在处取极小值,即最小值为.
……
6分
若,,则,即.
不妨设,则.
……
8分
设(),则.
当时,;当时,,
所以在上单调递增;在上单调递减,
所以,即,
所以的最大值为.……
10分
(3)由(2)知,当时,无极大值,
当时,在和上单调递增;在上单调递减,
所以在处取极大值,
所以,即.
……
12分
设,即,
当,,所以;
当,,
由(2)知,,又,
所以,且不恒为零,
所以在上单调递增.
不等式,即为,所以,
即不等式的解集为.
……
16分
20.(1)由条件,,,,,
,,所以.
(2)①由,
,,,…,.
将上面的式子相加,得,
所以.
因为{an}的各项均为正数,故.
因为也适合上式,所以().
②
假设存在满足条件的k
,不妨设,
所以,
平方得,(
)
所以,
所以,
即
由(1)得,,即,
若,代入(
)式,求得不合,舍去;
若,结合(2)得,
所以,即,又且,
所以的可能取值为2,3,4,代入(
)式逐一计算,可求得.
21..由条件知,,即,即,……………6分
所以
解得
所以,的值分别为,.……………………………………………………10分
22.直线的直角坐标方程为,
圆的普通方程为,…………………………………………5分
圆心到直线的距离,解得或.…………10分
23.
(1)
在直三棱柱ABCA1B1C1中,有AB⊥AC,AA1⊥AB,AA1⊥AC,
故可以{,,}为正交基底,建立如图所示的空间直角坐标系.(1分)
因为AB=2,AC=4,AA1=3,
所以A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3).
因为D是BC的中点,所以D(1,2,0).
所以=(-1,2,3).
设n1=(x1,y1,z1)为平面A1B1D的法向量,
因为=(2,0,0),=(-1,2,-3),
所以即
令y1=3,则x1=0,z1=2,所以平面A1B1D的一个法向量为n1=(0,3,2).(3分)
设直线DC1与平面A1B1D所成的角为θ,
则sin
θ=|cos?,n1?|==,
所以直线DC1与平面A1B1D所成角的正弦值为.(5分)
(2)
由(1)知=(-1,2,3),=(-2,4,0),
设n2=(x2,y2,z2)为平面B1DC1的法向量,
则即
令x2=2,则y2=1,z2=0,所以平面B1DC1的一个法向量为n2=(2,1,0).(7分)
同理可以求得平面A1DC1的一个法向量n3=(3,0,1),
所以cos?n2,n3?==,(9分)
由图可知二面角B1DC1A1的余弦值为.(10分)
24.
(1)
A1=(x2+y2)cos
θ=(x2+y2)·=x2-y2,(1分)
B1=(x2+y2)sin
θ=(x2+y2)·=2xy.(2分)
(2)
①当n=1时,由(1)得A1=x2-y2,B1=2xy.
因为x,y为整数,
所以A1,B1均为整数,所以结论成立;(4分)
②当n=k(k≥2,k∈N
)时,假设Ak,Bk均为整数,
则当n=k+1时,Ak+1=(x2+y2)k+1cos
(k+1)θ
=(x2+y2)(x2+y2)k(cos
kθcos
θ-sin
kθsin
θ)
=(x2+y2)cos
θ·(x2+y2)kcos
kθ-(x2+y2)ksin
kθ·(x2+y2)sin
θ
=A1·Ak-B1·Bk.(9分)
因为A1,B1,均为整数,所以Ak+1也为整数,
即当n=k+1时,结论也成立.
综合①②得,对一切正整数n,An均为整数.(10分)
A
B
C
D
F
E
P
M
N
(第17题)
y
O
A
B
C
x
(第18题)
A
B
C
D
F
E
P
M
N
(第18题)
PAGE
-
2
-
同课章节目录
