高中数学人教版必修2课件:1.3空间几何体的表面积与体积(3课时共49张PPT)
文档属性
| 名称 | 高中数学人教版必修2课件:1.3空间几何体的表面积与体积(3课时共49张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 09:12:32 | ||
图片预览







文档简介
(共49张PPT)
1.3空间几何体的表
面与体积
1.3.1 柱体、椎体、台体
的表面积与体积
第一课时
问题1
问题预习
什么是空间几何体的表面积?什么是空间几何体的体积?(课本P23)
表面积是几何体表面的面积,它表示几何体表面的大小.
体积是几何体所占空间的大小
问题2
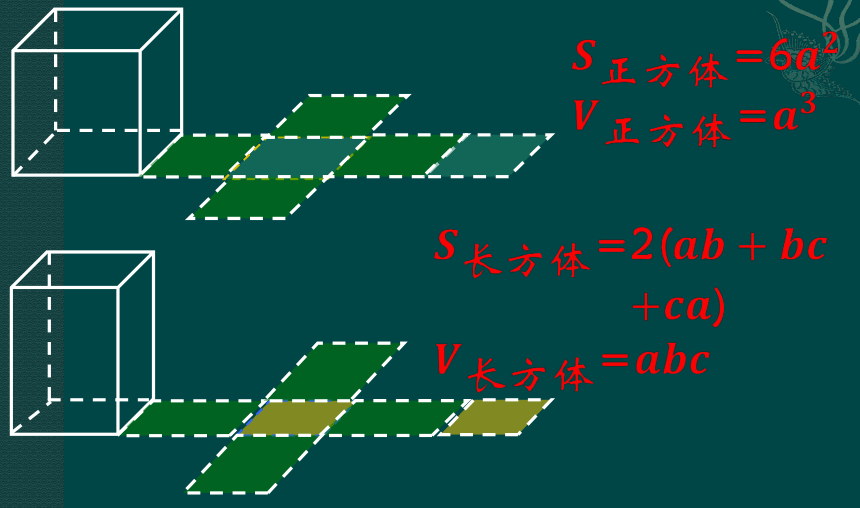
初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
?
?
问题3
在求长方体和正方体的表面积,用到了一个什么样的数学思想呢?
?
问题4
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
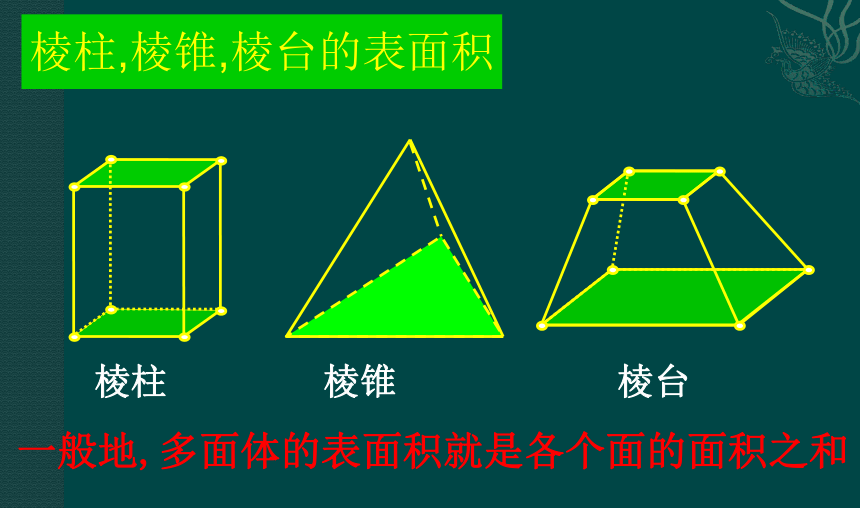
棱柱,棱锥,棱台的表面积
一般地,多面体的表面积就是各个面的面积之和
棱柱
棱锥
棱台
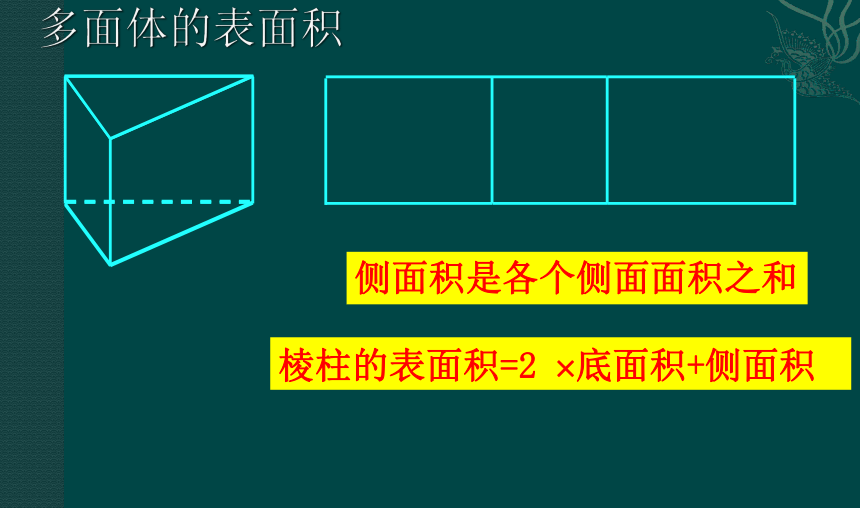
多面体的表面积
棱柱的表面积=2 ?底面积+侧面积
棱锥的表面积=底面积+侧面积
侧面积是各个侧面面积之和
棱台的表面积=上底面积+
下底面积+侧面积
多面体的表面积
棱柱的表面积=2 ?底面积+侧面积
侧面积是各个侧面面积之和
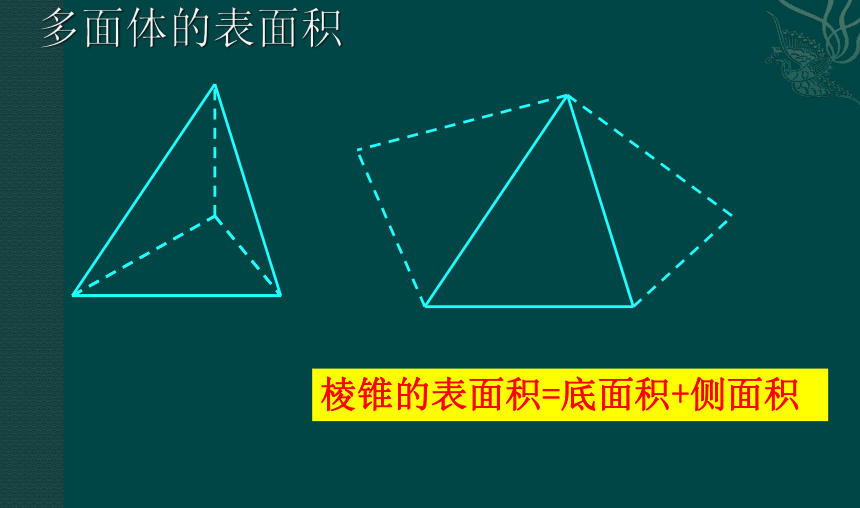
多面体的表面积
棱锥的表面积=底面积+侧面积
多面体的表面积
棱台的表面积=上底面积+
下底面积+侧面积
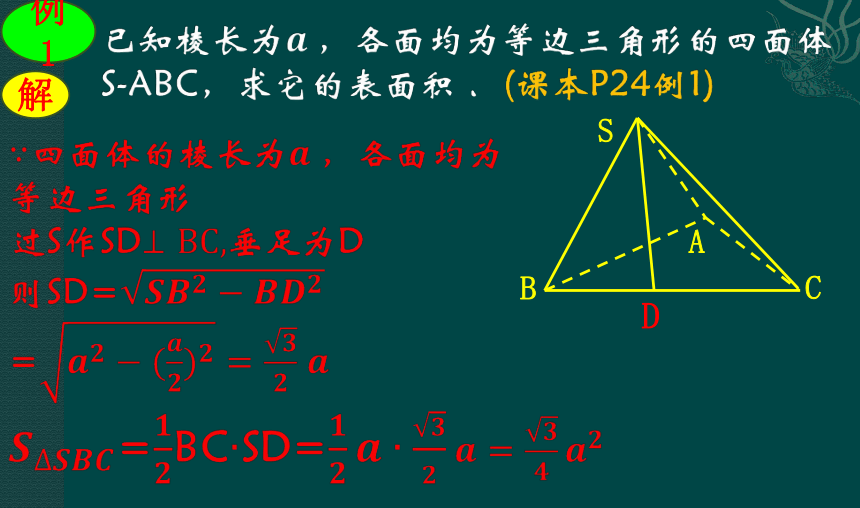
例1
?
S
A
B
C
解
?
D
?
问题5
圆柱的侧面展开图是什么?圆柱的侧面积和表面积怎样计算?
?
?
?
?
?
?
?
?
?
问题6
如何利用圆台的定义、圆锥的侧面积公式推
导圆台的侧面积和表面积公式?
?
?
?
?
?
?
?
?
问题7
圆柱、圆锥、圆台的表面积之间有什么关系吗?
O
O’
O
r=R
上底扩大
O
r=0
上底缩小
?
?
?
例2
如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?
?
解
题型1
已知几何体的三视图,求几何体的表面积
例3
一个正三棱柱的三视图如图所示(单位:cm),求这个三棱柱的表面积.
正视图
侧视图
府视图
?
2
解
?
变式
?
正视图
侧视图
府视图
?
例4
?
?
?
?
?
?
?
?
解
?
课堂练习
课本P27练习1、2
第二课时
问题8
初中我们学过正方体、长方体、圆柱的体积,它们的体积公式是?
?
这也是一般棱柱的体积公式.
问题9
什么是棱柱的高?
棱柱的高是指两底面之间的距离,即从一个底面上
任意一点向另一个底面作垂线,这点与垂足(.垂线与
底面的交点)之间的距离
A
B
C
D
?
?
?
?
?
?
?
?
?
问题10
圆锥(棱锥)的体积公式是什么?
?
圆锥(棱锥)的体积是同底等高的圆柱(棱柱)体积的
三分之一
问题11
什么是棱锥的高?
棱锥的高是指顶点到底面之间的距离,即从顶点向底面作垂线,这点与垂足(.垂线与底面的交点)之间的距离
?
?
?
?
?
?
?
?
?
?
?
?
问题10
棱台、圆台的体积怎样计算呢?又怎样推导呢?
?
?
?
?
?
问题11
比较柱体、锥体、台体的体积公式,你能发现它们三者之间有什么关系吗?
题型2
柱、锥、台的体积公式
例4
?
A
?
?
?
?
?
?
?
?
解
?
?
?
例5
有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个?
?
解
六角螺帽的个数为:
5.8×1000÷(7.8×2.956 )≈252(个)
第三课时
问题12
阅读教材P27的内容,球的
体积和表面积公式各是什么?
球是怎样定义的?
球是由半圆绕它的直径所在直线旋转一周所得的
几何体
?
?
?
问题13
?
?
?
例6
?
证明
设球的半径为R,则圆柱的底
面半径为R,高为2R.
?
?
例7
若三个球的表面积之比为1:2:3,求这三个球的体积之比
解
?
?
?
?
?
?
?
?
大圆:过球心的截面圆叫球的大圆.
小圆:不过球心的截面圆叫球的小圆.
例8
?
?
?
?
?
?
解
?
?
?
?
?
?
?
例9
已知三个球,第一个球内切于正方体的六个面,
第二个球与这个正方体的各条棱相切,第三个
球过这个正方体的各个顶点,求这三个球的表
面积之比
解
?
?
?
(1)
?
?
?
(2)
?
?
?
课本P28练习1、2、3
课内练习
课本P28习题1.3
A组、B组
作业
1.3空间几何体的表
面与体积
1.3.1 柱体、椎体、台体
的表面积与体积
第一课时
问题1
问题预习
什么是空间几何体的表面积?什么是空间几何体的体积?(课本P23)
表面积是几何体表面的面积,它表示几何体表面的大小.
体积是几何体所占空间的大小
问题2
初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
?
?
问题3
在求长方体和正方体的表面积,用到了一个什么样的数学思想呢?
?
问题4
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
棱柱,棱锥,棱台的表面积
一般地,多面体的表面积就是各个面的面积之和
棱柱
棱锥
棱台
多面体的表面积
棱柱的表面积=2 ?底面积+侧面积
棱锥的表面积=底面积+侧面积
侧面积是各个侧面面积之和
棱台的表面积=上底面积+
下底面积+侧面积
多面体的表面积
棱柱的表面积=2 ?底面积+侧面积
侧面积是各个侧面面积之和
多面体的表面积
棱锥的表面积=底面积+侧面积
多面体的表面积
棱台的表面积=上底面积+
下底面积+侧面积
例1
?
S
A
B
C
解
?
D
?
问题5
圆柱的侧面展开图是什么?圆柱的侧面积和表面积怎样计算?
?
?
?
?
?
?
?
?
?
问题6
如何利用圆台的定义、圆锥的侧面积公式推
导圆台的侧面积和表面积公式?
?
?
?
?
?
?
?
?
问题7
圆柱、圆锥、圆台的表面积之间有什么关系吗?
O
O’
O
r=R
上底扩大
O
r=0
上底缩小
?
?
?
例2
如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?
?
解
题型1
已知几何体的三视图,求几何体的表面积
例3
一个正三棱柱的三视图如图所示(单位:cm),求这个三棱柱的表面积.
正视图
侧视图
府视图
?
2
解
?
变式
?
正视图
侧视图
府视图
?
例4
?
?
?
?
?
?
?
?
解
?
课堂练习
课本P27练习1、2
第二课时
问题8
初中我们学过正方体、长方体、圆柱的体积,它们的体积公式是?
?
这也是一般棱柱的体积公式.
问题9
什么是棱柱的高?
棱柱的高是指两底面之间的距离,即从一个底面上
任意一点向另一个底面作垂线,这点与垂足(.垂线与
底面的交点)之间的距离
A
B
C
D
?
?
?
?
?
?
?
?
?
问题10
圆锥(棱锥)的体积公式是什么?
?
圆锥(棱锥)的体积是同底等高的圆柱(棱柱)体积的
三分之一
问题11
什么是棱锥的高?
棱锥的高是指顶点到底面之间的距离,即从顶点向底面作垂线,这点与垂足(.垂线与底面的交点)之间的距离
?
?
?
?
?
?
?
?
?
?
?
?
问题10
棱台、圆台的体积怎样计算呢?又怎样推导呢?
?
?
?
?
?
问题11
比较柱体、锥体、台体的体积公式,你能发现它们三者之间有什么关系吗?
题型2
柱、锥、台的体积公式
例4
?
A
?
?
?
?
?
?
?
?
解
?
?
?
例5
有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个?
?
解
六角螺帽的个数为:
5.8×1000÷(7.8×2.956 )≈252(个)
第三课时
问题12
阅读教材P27的内容,球的
体积和表面积公式各是什么?
球是怎样定义的?
球是由半圆绕它的直径所在直线旋转一周所得的
几何体
?
?
?
问题13
?
?
?
例6
?
证明
设球的半径为R,则圆柱的底
面半径为R,高为2R.
?
?
例7
若三个球的表面积之比为1:2:3,求这三个球的体积之比
解
?
?
?
?
?
?
?
?
大圆:过球心的截面圆叫球的大圆.
小圆:不过球心的截面圆叫球的小圆.
例8
?
?
?
?
?
?
解
?
?
?
?
?
?
?
例9
已知三个球,第一个球内切于正方体的六个面,
第二个球与这个正方体的各条棱相切,第三个
球过这个正方体的各个顶点,求这三个球的表
面积之比
解
?
?
?
(1)
?
?
?
(2)
?
?
?
课本P28练习1、2、3
课内练习
课本P28习题1.3
A组、B组
作业
