高中数学人教版必修5课件:2.4等比数列(共41张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:2.4等比数列(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 09:13:19 | ||
图片预览










文档简介
(共41张PPT)
2.4等比数列
第一课时
问题1
阅读教材P48-49观察数列①②③④有什么共同特点?
问题2
什么是等比数列?什么是等比数列的公比?类比等差数列,你能否定义呢?
问题3
上述四个数列是等比数列吗?如果是,公比各
是多少?
问题4
?
问题5
类比等差中项的定义 ,你能给等比中项一个
定义吗?(P49)
问题6
?
问题7
你能举几个生活中等比数列的实例吗?
问题8
类比等差数列通项公式的归纳过程,你能
归纳一下等比数列的通项公式吗?
类比等差数列通项公式的推证过程,你能
根据等比数列的定义,推导出等比数列的通项公式吗?
问题9
问题1
阅读教材P48-49观察数列①②③④有什么共同特点?
?
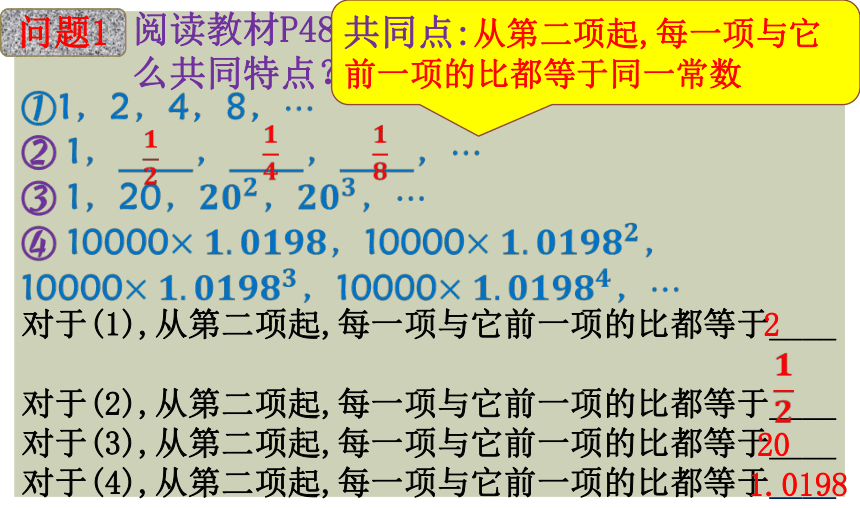
对于(1),从第二项起,每一项与它前一项的比都等于____
对于(2),从第二项起,每一项与它前一项的比都等于____
对于(3),从第二项起,每一项与它前一项的比都等于____
对于(4),从第二项起,每一项与它前一项的比都等于____
2
20
1.0198
?
共同点:从第二项起,每一项与它前一项的比都等于同一常数
?
?
?
问题2
什么是等比数列?什么是等比数列的公差?类比等差数列,你能否定义呢?
?
问题3
上述四个数列是等比数列吗?如果是,公比各
是多少?
?
问题4
?
?
问题5
类比等差中项的定义 ,你能给等比中项一个
定义吗?(P49)
?
问题6
?
?
问题7
你能举几个生活中等比数列的实例吗?
人口增长模型、储蓄存款利息、购房(购车)贷款、资产折旧等
问题8
类比等差数列通项公式的归纳过程,你能
归纳一下等比数列的通项公式吗?
?
问题9
类比等差数列通项公式的推证过程,你能
根据等比数列的定义,推导出等比数列的通项公式吗?
?
?
第二课时
探究:等比数列与指数函数的关系
作出课本P50上的图象
应 用
题型1
等比数列的通项公式
例1
某种放射性物质不断变化为其它物质,每经过一年剩留的这种物质是原来的84%,这种物质的半衰期为多长?(精确到1年)
例2
一个等比数列的第3项,第4项分别是12和18,
求它的第1项和第2项(课本P51)
解
?
例3
?
解
?
题型2
等比数列的定义
例4
?
答案:A (只有(4)正确)
例5
?
证明
?
题型3
等比数列的判定
例6
?
?
解
例7
?
解
?
?
题型4
等比数列的单调性
问题10
?
?
?
?
?
第三课时
类比等差数列的性质,结合课本P53的练习3、4 你能推导出等比数列的哪些性质?
?
?
?
?
?
?
?
题型5
等比数列性质的应用
例8
(1)三个数是等比数列,其积为512,若第一个数与第三个数都减去2,则这三个数成等差数列,求这三个数
解1
?
解2
?
(2)有四个数,前三个数成等比数列,后三个数成等差
数列,首末两项的和为21,中间两项的和为18,求
这四个数
第四课时
解1
?
解2
?
(从首、末两项及中间两项的和入手)
解3
?
数列通项公式的求法
题型1
等差数列、等比数列,直接用公式
题型3
?
?
题型2
?
?
例9
?
解
?
题型4
?
?
例9
?
例8
解
?
?
题型5
?
?
例10
?
解
?
?
题型6
?
?
例11
?
证明
?
?
题型7
?
?
例12
?
解
?
题型8
?
?
?
?
例13
?
解
?
题型9
?
?
解
?
例14
?
?
题型10
?
?
例14
解
?
2.4等比数列
第一课时
问题1
阅读教材P48-49观察数列①②③④有什么共同特点?
问题2
什么是等比数列?什么是等比数列的公比?类比等差数列,你能否定义呢?
问题3
上述四个数列是等比数列吗?如果是,公比各
是多少?
问题4
?
问题5
类比等差中项的定义 ,你能给等比中项一个
定义吗?(P49)
问题6
?
问题7
你能举几个生活中等比数列的实例吗?
问题8
类比等差数列通项公式的归纳过程,你能
归纳一下等比数列的通项公式吗?
类比等差数列通项公式的推证过程,你能
根据等比数列的定义,推导出等比数列的通项公式吗?
问题9
问题1
阅读教材P48-49观察数列①②③④有什么共同特点?
?
对于(1),从第二项起,每一项与它前一项的比都等于____
对于(2),从第二项起,每一项与它前一项的比都等于____
对于(3),从第二项起,每一项与它前一项的比都等于____
对于(4),从第二项起,每一项与它前一项的比都等于____
2
20
1.0198
?
共同点:从第二项起,每一项与它前一项的比都等于同一常数
?
?
?
问题2
什么是等比数列?什么是等比数列的公差?类比等差数列,你能否定义呢?
?
问题3
上述四个数列是等比数列吗?如果是,公比各
是多少?
?
问题4
?
?
问题5
类比等差中项的定义 ,你能给等比中项一个
定义吗?(P49)
?
问题6
?
?
问题7
你能举几个生活中等比数列的实例吗?
人口增长模型、储蓄存款利息、购房(购车)贷款、资产折旧等
问题8
类比等差数列通项公式的归纳过程,你能
归纳一下等比数列的通项公式吗?
?
问题9
类比等差数列通项公式的推证过程,你能
根据等比数列的定义,推导出等比数列的通项公式吗?
?
?
第二课时
探究:等比数列与指数函数的关系
作出课本P50上的图象
应 用
题型1
等比数列的通项公式
例1
某种放射性物质不断变化为其它物质,每经过一年剩留的这种物质是原来的84%,这种物质的半衰期为多长?(精确到1年)
例2
一个等比数列的第3项,第4项分别是12和18,
求它的第1项和第2项(课本P51)
解
?
例3
?
解
?
题型2
等比数列的定义
例4
?
答案:A (只有(4)正确)
例5
?
证明
?
题型3
等比数列的判定
例6
?
?
解
例7
?
解
?
?
题型4
等比数列的单调性
问题10
?
?
?
?
?
第三课时
类比等差数列的性质,结合课本P53的练习3、4 你能推导出等比数列的哪些性质?
?
?
?
?
?
?
?
题型5
等比数列性质的应用
例8
(1)三个数是等比数列,其积为512,若第一个数与第三个数都减去2,则这三个数成等差数列,求这三个数
解1
?
解2
?
(2)有四个数,前三个数成等比数列,后三个数成等差
数列,首末两项的和为21,中间两项的和为18,求
这四个数
第四课时
解1
?
解2
?
(从首、末两项及中间两项的和入手)
解3
?
数列通项公式的求法
题型1
等差数列、等比数列,直接用公式
题型3
?
?
题型2
?
?
例9
?
解
?
题型4
?
?
例9
?
例8
解
?
?
题型5
?
?
例10
?
解
?
?
题型6
?
?
例11
?
证明
?
?
题型7
?
?
例12
?
解
?
题型8
?
?
?
?
例13
?
解
?
题型9
?
?
解
?
例14
?
?
题型10
?
?
例14
解
?
