高中数学人教A版必修1课件:3.1.1方程的根与函数的零点(共24张PPT)
文档属性
| 名称 | 高中数学人教A版必修1课件:3.1.1方程的根与函数的零点(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 651.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 14:52:03 | ||
图片预览





文档简介
(共25张PPT)
思考1.
一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?
方 程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函 数
函
数
的
图
象
方程的实数根
x1=-1 , x2=3
x1=x2=1
无实数根
(-1,0),(3,0)
(1,0)
无交点
x2-2x-3=0
y= x2-2x+3
函数的图像
与x轴的交点
方程ax2 +bx+c=0
(a≠0)的根
函数
y=ax2 +bx+c
(a>0)的图象
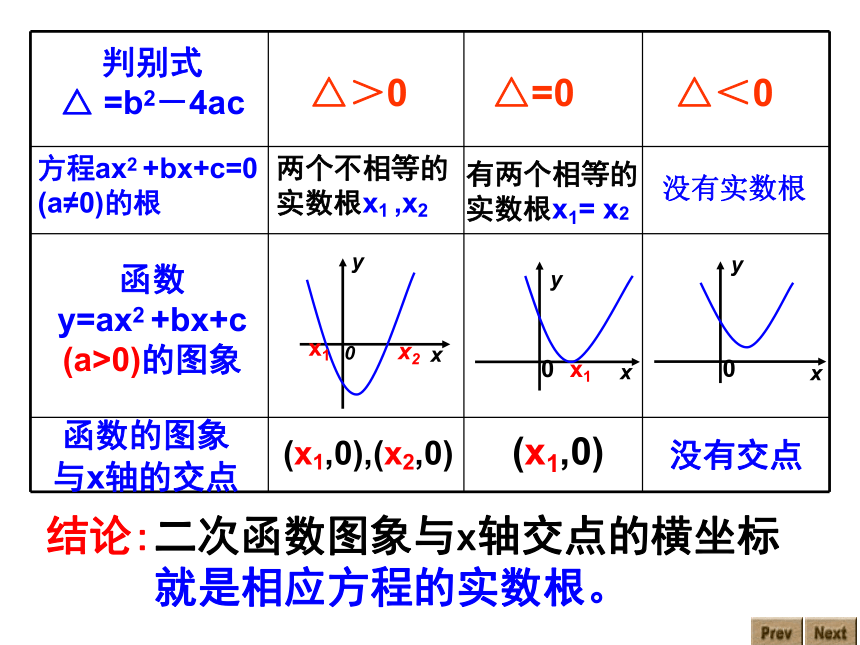
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与x轴的交点
有两个相等的
实数根x1= x2
没有实数根
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等的
实数根x1 ,x2
结论:二次函数图象与x轴交点的横坐标
就是相应方程的实数根。
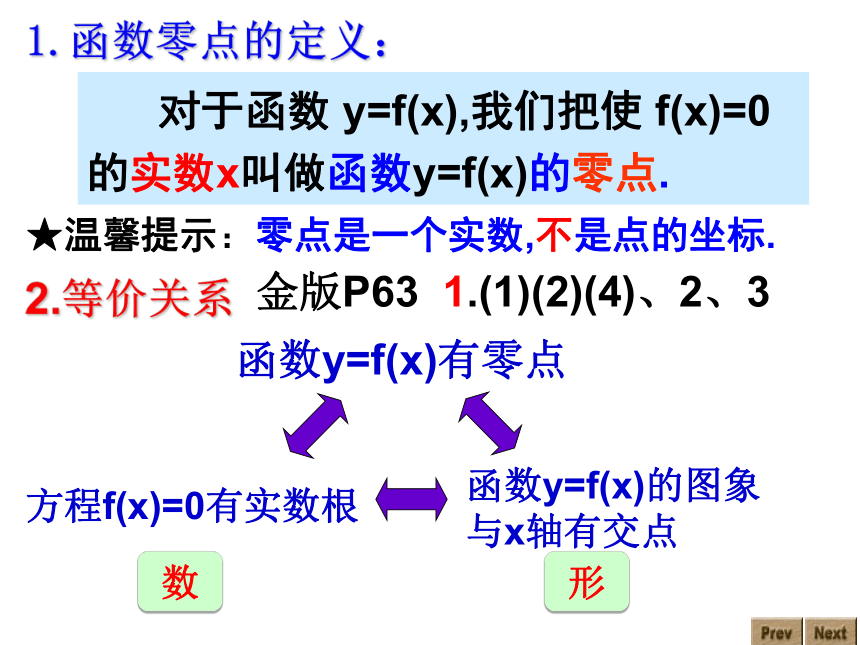
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数y=f(x)的零点.
1.函数零点的定义:
2.等价关系
★温馨提示:零点是一个实数,不是点的坐标.
金版P63 1.(1)(2)(4)、2、3
方程f(x)=0有实数根
函数y=f(x)的图象
与x轴有交点
函数y=f(x)有零点
数
形
方程ax2 +bx+c=0
(a≠0)的根
函数
y=ax2 +bx+c
(a>0)的图象
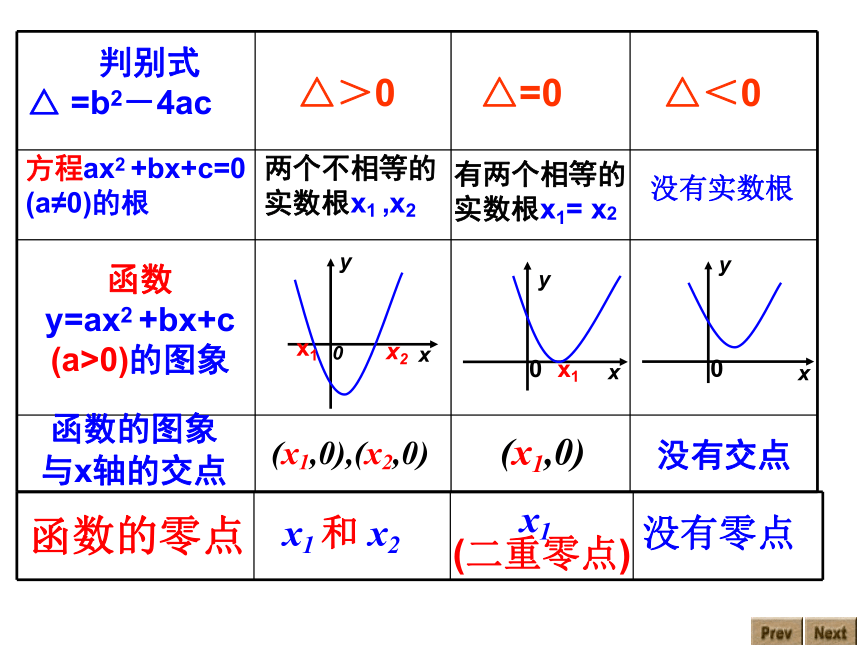
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与x轴的交点
有两个相等的
实数根x1= x2
没有实数根
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等的
实数根x1 ,x2
函数的零点
x1 和 x2
x1
没有零点
(二重零点)
求函数y=f(x)的零点即求方程f(x)=0的实数根,也即是求函数y=f(x)的图象与x轴交点的横坐标.
小结:求函数零点的方法:
(1)解方程法(2)数形结合法
(3)若函数f(x)=x2-ax-b的两个零点是2和3, 则a=_______,b=________
金版P63 类型1
思考2.
(1)函数都有零点吗?
(2)什么条件下的函数必有零点?
课本P87 探究
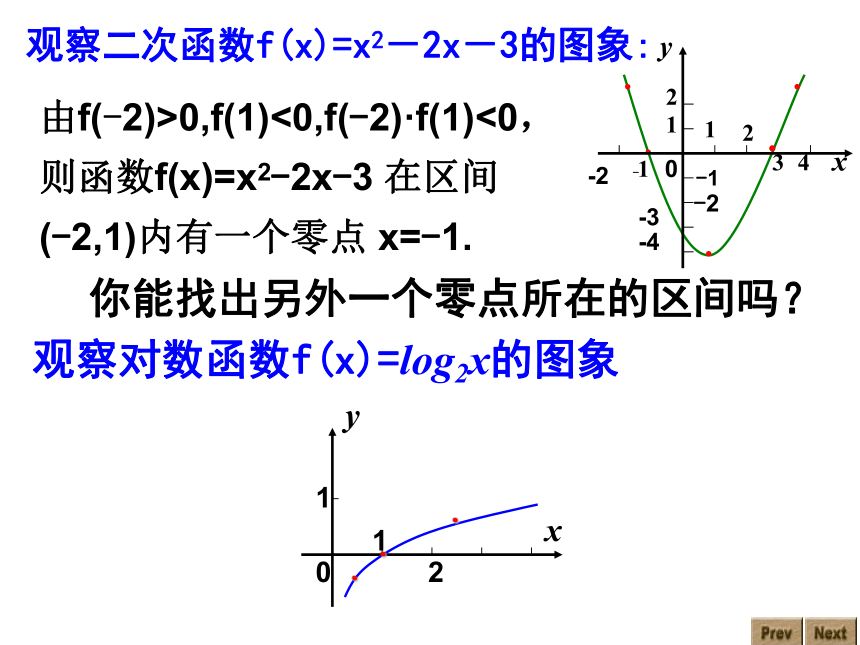
观察二次函数f(x)=x2-2x-3的图象:
由f(-2)>0,f(1)<0,f(-2)·f(1)<0,
则函数f(x)=x2-2x-3 在区间 (-2,1)内有一个零点 x=-1.
你能找出另外一个零点所在的区间吗?
观察对数函数f(x)=log2x的图象
答:不一定. 若函数y=f(x)在区间[a,b]上的图象是连续的,则 f(x)必有零点;
如果不连续,就可能没有零点.
思考3.若函数y=f(x)在区间[a,b]上满足
f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内一定有零点吗?
建构新知:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
思考4.满足上述两个条件,函数就在指定区间
内存在零点,那么,零点是否只有一个?
注意:该定理只能说明函数存在变号零点,
但不能判断个数.
零点存在性定理:
课本P92 2
作业: 金版P64
总结:若函数y=f(x)在区间[a,b]上连续,则:
此时,若函数y=f(x)在[a,b]是单调的,则f(x)在(a,b)内有唯一的零点。
金版P64 类型2
由表和图可知f(2)<0,f(3)>0,
即f(2)·f(3)<0,
∴ f(x)在区间(2,3)内有零点.
∵函数f(x)在定义域(0,+∞)内是增函数,
∴函数f(x)=lnx+2x-6仅有一个零点.
解:用计算器或计算机作出x、f(x)的对应值表和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
例1.求函数f(x)=lnx+2x-6的零点个数.
y=-2x+6
y=lnx
即求方程lnx+2x-6=0的实数解的个数,
即求lnx=6-2x的实数解的个数,
即判断函数y=lnx与函数y=6-2x的交点个数.
解法二:
例1. 求函数f(x)=lnx+2x-6的零点的个数.
例1. 求函数f(x)=lnx+2x-6的零点的个数.
变式1.求函数f(x)=lnx-x+3的零点的个数.
解法二: 作出函数y=lnx和y=6-2x的图象
y=6-2x
y=x-3
y=lnx
关键:分离基本初等函数.
金版P64 类型3
变式2.若函数f(x)为定义在R上的奇函数,且 当x>0时,f(x)=lnx+2x-6,
(1)判断函数y=f(x)的零点的个数;
(2)求函数y=f(x)所有零点之和;
(3)如果R上的奇函数有零点,
试问:零点个数有什么特点?
所有零点之和你能得出什么
结论吗?偶函数呢?
例1. 求函数f(x)=lnx+2x-6的零点的个数.
金版P64 课堂小结
报纸第8期 第1版
作业:报纸第8期 D2版3.1.1
+考题精选1、7+金版P65
二次函数问题的主要类型
1.解析式(注:二次函数解析式的3 种形式)
(1) 一般式:
(2) 顶点式:
(3) 两根式:
2. 与图象和性质有关问题(识图,单调性,最值)
3. 二次函数在给定区间[a,b]的最值问题
4. 己知根的分布求参数范围问题
5. 以二次函数为背景的不等式问题
y=ax2+bx+c (a≠0)
y=a(x-x1)(x-x2) (a≠0)
y=a(x-m)2+n (a≠0)
一元二次方程的实根分布问题
一元二次方程根的分布 可转化为一元二次函数零点的分布问题: ①开口方向 ②△的符号 ③对称轴位置 ④区间端点函数值的正负
例.若方程 x?+(m–3)x+m=0的两实根为x1,x2, 分别在下列条件下,求实数m的取值范围.
设 f(x)=x?+(m–3)x+m
(1)方程有两个正实根
(2)方程两个根均小于1
(4)方程一个根大于1,一个根小于1
(3)若方程的两个根均在(0,2)内
(6)方程一个根在(–2,0),另一个根在(1,4)
(5)方程一个根小于2, 另一个根大于4
两个根均小于k
两个根均大于k
小结:一般地,一元二次方程ax?+bx+c=0(a>0)的实根分布
两个根均在
(m,n)内
x1∈(m,n) ,
x2∈(p,q)
一根小于m,
一根大于n
一个根小于k,
一个根大于k.
小结:一般地,一元二次方程ax?+bx+c=0(a>0)的实根分布
一元二次方程根的分布 可转化为一元二次函数零点的分布问题: ①开口方向 ②△的符号 ③对称轴位置 ④区间端点函数值的正负
作业:报纸第8期 D3 B卷 6
金版学案 P65、P80
预习:课本P89~90 二分法
思考1.
一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?
方 程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函 数
函
数
的
图
象
方程的实数根
x1=-1 , x2=3
x1=x2=1
无实数根
(-1,0),(3,0)
(1,0)
无交点
x2-2x-3=0
y= x2-2x+3
函数的图像
与x轴的交点
方程ax2 +bx+c=0
(a≠0)的根
函数
y=ax2 +bx+c
(a>0)的图象
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与x轴的交点
有两个相等的
实数根x1= x2
没有实数根
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等的
实数根x1 ,x2
结论:二次函数图象与x轴交点的横坐标
就是相应方程的实数根。
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数y=f(x)的零点.
1.函数零点的定义:
2.等价关系
★温馨提示:零点是一个实数,不是点的坐标.
金版P63 1.(1)(2)(4)、2、3
方程f(x)=0有实数根
函数y=f(x)的图象
与x轴有交点
函数y=f(x)有零点
数
形
方程ax2 +bx+c=0
(a≠0)的根
函数
y=ax2 +bx+c
(a>0)的图象
判别式
△ =b2-4ac
△>0
△=0
△<0
函数的图象
与x轴的交点
有两个相等的
实数根x1= x2
没有实数根
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等的
实数根x1 ,x2
函数的零点
x1 和 x2
x1
没有零点
(二重零点)
求函数y=f(x)的零点即求方程f(x)=0的实数根,也即是求函数y=f(x)的图象与x轴交点的横坐标.
小结:求函数零点的方法:
(1)解方程法(2)数形结合法
(3)若函数f(x)=x2-ax-b的两个零点是2和3, 则a=_______,b=________
金版P63 类型1
思考2.
(1)函数都有零点吗?
(2)什么条件下的函数必有零点?
课本P87 探究
观察二次函数f(x)=x2-2x-3的图象:
由f(-2)>0,f(1)<0,f(-2)·f(1)<0,
则函数f(x)=x2-2x-3 在区间 (-2,1)内有一个零点 x=-1.
你能找出另外一个零点所在的区间吗?
观察对数函数f(x)=log2x的图象
答:不一定. 若函数y=f(x)在区间[a,b]上的图象是连续的,则 f(x)必有零点;
如果不连续,就可能没有零点.
思考3.若函数y=f(x)在区间[a,b]上满足
f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内一定有零点吗?
建构新知:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
思考4.满足上述两个条件,函数就在指定区间
内存在零点,那么,零点是否只有一个?
注意:该定理只能说明函数存在变号零点,
但不能判断个数.
零点存在性定理:
课本P92 2
作业: 金版P64
总结:若函数y=f(x)在区间[a,b]上连续,则:
此时,若函数y=f(x)在[a,b]是单调的,则f(x)在(a,b)内有唯一的零点。
金版P64 类型2
由表和图可知f(2)<0,f(3)>0,
即f(2)·f(3)<0,
∴ f(x)在区间(2,3)内有零点.
∵函数f(x)在定义域(0,+∞)内是增函数,
∴函数f(x)=lnx+2x-6仅有一个零点.
解:用计算器或计算机作出x、f(x)的对应值表和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
例1.求函数f(x)=lnx+2x-6的零点个数.
y=-2x+6
y=lnx
即求方程lnx+2x-6=0的实数解的个数,
即求lnx=6-2x的实数解的个数,
即判断函数y=lnx与函数y=6-2x的交点个数.
解法二:
例1. 求函数f(x)=lnx+2x-6的零点的个数.
例1. 求函数f(x)=lnx+2x-6的零点的个数.
变式1.求函数f(x)=lnx-x+3的零点的个数.
解法二: 作出函数y=lnx和y=6-2x的图象
y=6-2x
y=x-3
y=lnx
关键:分离基本初等函数.
金版P64 类型3
变式2.若函数f(x)为定义在R上的奇函数,且 当x>0时,f(x)=lnx+2x-6,
(1)判断函数y=f(x)的零点的个数;
(2)求函数y=f(x)所有零点之和;
(3)如果R上的奇函数有零点,
试问:零点个数有什么特点?
所有零点之和你能得出什么
结论吗?偶函数呢?
例1. 求函数f(x)=lnx+2x-6的零点的个数.
金版P64 课堂小结
报纸第8期 第1版
作业:报纸第8期 D2版3.1.1
+考题精选1、7+金版P65
二次函数问题的主要类型
1.解析式(注:二次函数解析式的3 种形式)
(1) 一般式:
(2) 顶点式:
(3) 两根式:
2. 与图象和性质有关问题(识图,单调性,最值)
3. 二次函数在给定区间[a,b]的最值问题
4. 己知根的分布求参数范围问题
5. 以二次函数为背景的不等式问题
y=ax2+bx+c (a≠0)
y=a(x-x1)(x-x2) (a≠0)
y=a(x-m)2+n (a≠0)
一元二次方程的实根分布问题
一元二次方程根的分布 可转化为一元二次函数零点的分布问题: ①开口方向 ②△的符号 ③对称轴位置 ④区间端点函数值的正负
例.若方程 x?+(m–3)x+m=0的两实根为x1,x2, 分别在下列条件下,求实数m的取值范围.
设 f(x)=x?+(m–3)x+m
(1)方程有两个正实根
(2)方程两个根均小于1
(4)方程一个根大于1,一个根小于1
(3)若方程的两个根均在(0,2)内
(6)方程一个根在(–2,0),另一个根在(1,4)
(5)方程一个根小于2, 另一个根大于4
两个根均小于k
两个根均大于k
小结:一般地,一元二次方程ax?+bx+c=0(a>0)的实根分布
两个根均在
(m,n)内
x1∈(m,n) ,
x2∈(p,q)
一根小于m,
一根大于n
一个根小于k,
一个根大于k.
小结:一般地,一元二次方程ax?+bx+c=0(a>0)的实根分布
一元二次方程根的分布 可转化为一元二次函数零点的分布问题: ①开口方向 ②△的符号 ③对称轴位置 ④区间端点函数值的正负
作业:报纸第8期 D3 B卷 6
金版学案 P65、P80
预习:课本P89~90 二分法
