北师大版数学八年级下册:2.2 不等式的基本性质 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学八年级下册:2.2 不等式的基本性质 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-29 15:24:04 | ||
图片预览






文档简介
(共16张PPT)
第二章 一元一次不等式与一元一次不等式组
第二节 不等式的基本性质
同一个代数式
等式的两边都加(或减)____________,等式仍然成立。
等式的基本性质1:
(或除以同一个不为零的数)
等式的两边同时乘同一个数
____________________________,等式仍然成立。
等式的基本性质2:
复习旧知:你还记得等式的基本性质吗?
如果a=b,则ac=bc
如果a=b,则a/c=b/c (c≠ 0)
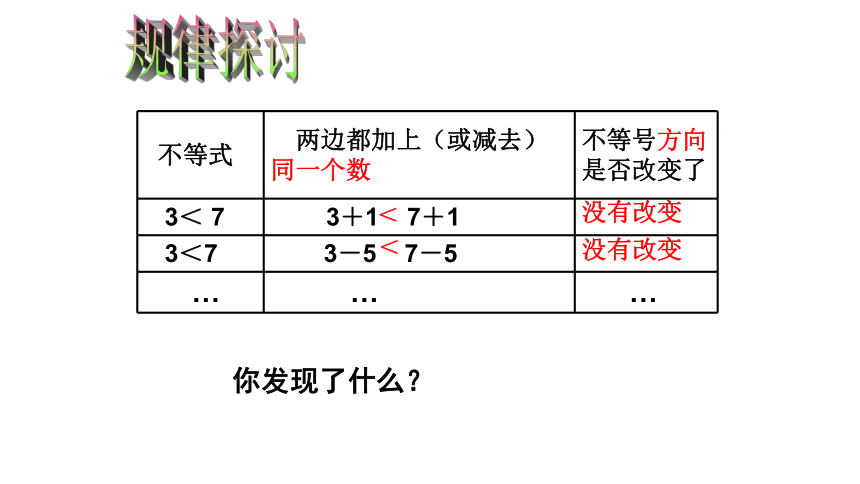
规律探讨
不等式 两边都加上(或减去)同一个数 不等号方向是否改变了
3< 7 3+1 7+1
3<7 3-5 7-5
… … …
没有改变
没有改变
你发现了什么?
<
<
不等式的性质1:
不等式的两边都加(或减)同一个整式,不等号的方向不变。
将不等式2<3的两边都乘以同一个不为0的数比较所得结果。
2 < 3
2×1( )3×1,
2×2( )3×2,
2×3( )3×3,
2×4( )3×4,
两边都乘以同一个正数,不等号的方向不变;
<
<
<
<
规律探讨
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的性质2
如果a>b, ,
c>0
那么ac>bc ,
2 < 3
2×(-1)( )3×(-1),
2×(-2)( )3×(-2),
2×(-3)( )3×(-3),
2×(-4)( )3×(-4),
…
将不等式2<3的两边都乘以同一个不为0的数,比较所得结果。
>
>
>
>
不等式的两边都乘以同一个负数,不等号的方向改变;
规律探讨
不等式的两边都乘(或除以)同一个负数,不等号的方向改变;
不等式的性质3
如果a>b,
c<0 ,
那么ac例1:利用不等式的性质将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>?1; (2)?2x>3;
解: (1)根据不等式
的性质1两边都加上5,
得:
x > ?1+5
即x >4;
解:(2)根据不等式
的性质3两边都除以?2,
得:
x < 3÷(?2)
即x <- -;
2
3
小练习:将下列不等式化成
X > a或 x < a的形式
(1) x-1 2
(2) -x
(3) 0.5x 3
>
<
<
6
5
?
例2 用“>”或“<”填空:
(1)a+3_____b+3;(ab);
(3) (a>b);
(4)a-4_____b-4 (a-b>0) ;
<
<
>
>
小练习:
如果a>b,那么
(1)a-5 __ b-5 (不等式性质___)
(2)5a___ 5b (不等式性质___)
(3)-3a___-3b (不等式性质___)
(4)a-b ___ 0 (不等式性质___)
(不等式性质___)
>
<
>
>
>
2
3
1
2
1
1.判断下列各题的推导是否正确?为什么 ?
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4, 所以a>-4;
(3)因为4a>4b, 所以a>b;
(4)因为-1>-2, 所以-a-1>-a-2;
(5)因为3>2, 所以3a>2a.
2.若 ,则 x ___
3. 若 ,满足此不等式的最
大整数为_____.
<
-4
4.将不等式 ax + 3 ≥ x – 1化成“x ≥ m”或“x ≤ n”的形式.
5.比较3a+5与10-2a的大小.
能力提升:
说一说
收获和体会
1. 不等式的基本性质是什么?
2. 和等式的基本性质相比,有 什么相同和不同之处?
3. 本节课你还有什么收获?
第二章 一元一次不等式与一元一次不等式组
第二节 不等式的基本性质
同一个代数式
等式的两边都加(或减)____________,等式仍然成立。
等式的基本性质1:
(或除以同一个不为零的数)
等式的两边同时乘同一个数
____________________________,等式仍然成立。
等式的基本性质2:
复习旧知:你还记得等式的基本性质吗?
如果a=b,则ac=bc
如果a=b,则a/c=b/c (c≠ 0)
规律探讨
不等式 两边都加上(或减去)同一个数 不等号方向是否改变了
3< 7 3+1 7+1
3<7 3-5 7-5
… … …
没有改变
没有改变
你发现了什么?
<
<
不等式的性质1:
不等式的两边都加(或减)同一个整式,不等号的方向不变。
将不等式2<3的两边都乘以同一个不为0的数比较所得结果。
2 < 3
2×1( )3×1,
2×2( )3×2,
2×3( )3×3,
2×4( )3×4,
两边都乘以同一个正数,不等号的方向不变;
<
<
<
<
规律探讨
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
不等式的性质2
如果a>b, ,
c>0
那么ac>bc ,
2 < 3
2×(-1)( )3×(-1),
2×(-2)( )3×(-2),
2×(-3)( )3×(-3),
2×(-4)( )3×(-4),
…
将不等式2<3的两边都乘以同一个不为0的数,比较所得结果。
>
>
>
>
不等式的两边都乘以同一个负数,不等号的方向改变;
规律探讨
不等式的两边都乘(或除以)同一个负数,不等号的方向改变;
不等式的性质3
如果a>b,
c<0 ,
那么ac
(1)x-5>?1; (2)?2x>3;
解: (1)根据不等式
的性质1两边都加上5,
得:
x > ?1+5
即x >4;
解:(2)根据不等式
的性质3两边都除以?2,
得:
x < 3÷(?2)
即x <- -;
2
3
小练习:将下列不等式化成
X > a或 x < a的形式
(1) x-1 2
(2) -x
(3) 0.5x 3
>
<
<
6
5
?
例2 用“>”或“<”填空:
(1)a+3_____b+3;(a
(3) (a>b);
(4)a-4_____b-4 (a-b>0) ;
<
<
>
>
小练习:
如果a>b,那么
(1)a-5 __ b-5 (不等式性质___)
(2)5a___ 5b (不等式性质___)
(3)-3a___-3b (不等式性质___)
(4)a-b ___ 0 (不等式性质___)
(不等式性质___)
>
<
>
>
>
2
3
1
2
1
1.判断下列各题的推导是否正确?为什么 ?
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4, 所以a>-4;
(3)因为4a>4b, 所以a>b;
(4)因为-1>-2, 所以-a-1>-a-2;
(5)因为3>2, 所以3a>2a.
2.若 ,则 x ___
3. 若 ,满足此不等式的最
大整数为_____.
<
-4
4.将不等式 ax + 3 ≥ x – 1化成“x ≥ m”或“x ≤ n”的形式.
5.比较3a+5与10-2a的大小.
能力提升:
说一说
收获和体会
1. 不等式的基本性质是什么?
2. 和等式的基本性质相比,有 什么相同和不同之处?
3. 本节课你还有什么收获?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
