人教版数学必修1 1.1.1 集合的含义与表示 (共17张PPT)
文档属性
| 名称 | 人教版数学必修1 1.1.1 集合的含义与表示 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 15:05:14 | ||
图片预览





文档简介
(共17张PPT)
1.1.1集合的含义及表示
第一章 集合
讨 论1
军训前学校通知:8月15日8点,高一年段
在体育馆集合进行军训动员;试问这个通
知的对象是全体的高一学生还是个别学生?
问:这个通知的对象是全体的高一级学生
还是个别学生?
概念认识
知识点1:元素与集合的概念及关系
(1)一般地,把 统称为元素,通常用
表示.
(2)把 叫做集合,通常用
表示.
一些元素组成的总体
大写字母
研究对象
小写字母
概念认识
知识点1:元素与集合的概念及关系
(3)元素与集合的关系
若a在集合A中,就说a属于集合A,记作a∈A;
若a不在集合A中,就说a不属于集合A,记作a A
.
讨论2
请同学们回忆我们已经接触过的一些集合
1.初中代数中对不等式的解集是怎么定义的?
含有未知数的不等式的所有解就组成了这个不等式的解的集合,简称这个不等式的解集。
2.初中几何中对圆是如何定义的呢?
到一定点的距离等于定长的点的集合就构成了圆。
讨论3
1.你能举出一些集合的例子吗?
合作探究
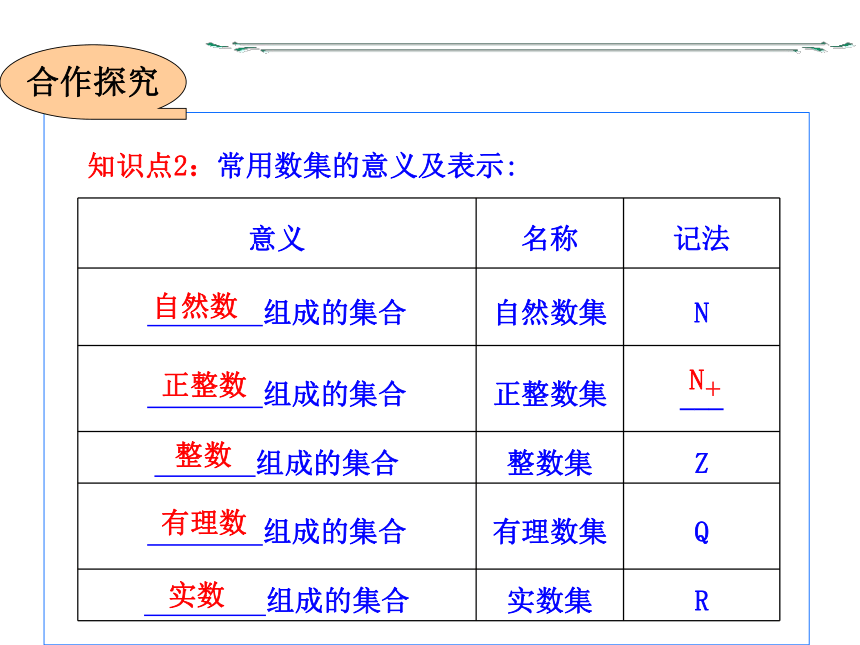
知识点2:常用数集的意义及表示:
自然数
正整数
整数
有理数
实数
N+
意义 名称 记法
组成的集合 自然数集 N
组成的集合 正整数集 ___
组成的集合 整数集 Z
组成的集合 有理数集 Q
组成的集合 实数集 R
讨论3
1. 集合元素有什么性质特征?
练习
思考
1.“高个子的同学”、“我国的小河流”能构成集合吗?
【提示】“高个子”是一个含糊不清的概念,具有相对性,多高才算高?同样地,“小河流”的“小”具体指什么,是流量还是长度?它们都没有明确的标准,也就是说,它们都是一些不能够确定的对象.因此,它们都不能构成集合.
确定性
知识点3:集合元素的性质特征
(1) ;
(2) ;
(3) .
无序性
确定性
互异性
练习
2.“由1,2,2,4,2,1能构成一个集合,这个集合中共有6个元素”这一说法是否正确?
【提示】在1,2,2,4,2,1中,只有3个不同的数(对象)1,
2,4,并且都是确定的不同对象.因此,它们能构成集合,但在这个集合中只有3个元素.
互异性
练习
3.集合A={1,2,3},B={3,2,1},集合A与集合B一样吗?
无序性
练习
例1 用列举法表示下列集合:
(1)由大于3小于10的整数组成的集合;
(2)方程 x2-9=0的解的集合.
解:(1)由大于3小于10的整数组成的集合用列举法可表示为{4,5,6,7,8,9};
(2)方程x2-9=0的解的集合用列举法可表示为{-3,3}.
练习
例2 用描述法表示下列集合:
(1)小于10的所有有理数组成的集合;
(2)所有偶数组成的集合.
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为
解:(1)小于10的所有有理数组成的集合用描述法可表示为
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为
解:(1)小于10的所有有理数组成的集合用描述法可表示为
练习
试分别用列举法和描述法 表示下列集合:
(1)方程 的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合.
知识点5:集合的分类
空集:不含有任何元素的集合
φ
有限集:含有限个元素的集合
无限集:含无限个元素的集合
1.集合与元素的概念及关系;
3.集合元素的性质:确定性;互异性;无序性;
2.常用数集及有关符号:
4.集合的表示方法:
5.集合的分类:
1.1.1集合的含义及表示
第一章 集合
讨 论1
军训前学校通知:8月15日8点,高一年段
在体育馆集合进行军训动员;试问这个通
知的对象是全体的高一学生还是个别学生?
问:这个通知的对象是全体的高一级学生
还是个别学生?
概念认识
知识点1:元素与集合的概念及关系
(1)一般地,把 统称为元素,通常用
表示.
(2)把 叫做集合,通常用
表示.
一些元素组成的总体
大写字母
研究对象
小写字母
概念认识
知识点1:元素与集合的概念及关系
(3)元素与集合的关系
若a在集合A中,就说a属于集合A,记作a∈A;
若a不在集合A中,就说a不属于集合A,记作a A
.
讨论2
请同学们回忆我们已经接触过的一些集合
1.初中代数中对不等式的解集是怎么定义的?
含有未知数的不等式的所有解就组成了这个不等式的解的集合,简称这个不等式的解集。
2.初中几何中对圆是如何定义的呢?
到一定点的距离等于定长的点的集合就构成了圆。
讨论3
1.你能举出一些集合的例子吗?
合作探究
知识点2:常用数集的意义及表示:
自然数
正整数
整数
有理数
实数
N+
意义 名称 记法
组成的集合 自然数集 N
组成的集合 正整数集 ___
组成的集合 整数集 Z
组成的集合 有理数集 Q
组成的集合 实数集 R
讨论3
1. 集合元素有什么性质特征?
练习
思考
1.“高个子的同学”、“我国的小河流”能构成集合吗?
【提示】“高个子”是一个含糊不清的概念,具有相对性,多高才算高?同样地,“小河流”的“小”具体指什么,是流量还是长度?它们都没有明确的标准,也就是说,它们都是一些不能够确定的对象.因此,它们都不能构成集合.
确定性
知识点3:集合元素的性质特征
(1) ;
(2) ;
(3) .
无序性
确定性
互异性
练习
2.“由1,2,2,4,2,1能构成一个集合,这个集合中共有6个元素”这一说法是否正确?
【提示】在1,2,2,4,2,1中,只有3个不同的数(对象)1,
2,4,并且都是确定的不同对象.因此,它们能构成集合,但在这个集合中只有3个元素.
互异性
练习
3.集合A={1,2,3},B={3,2,1},集合A与集合B一样吗?
无序性
练习
例1 用列举法表示下列集合:
(1)由大于3小于10的整数组成的集合;
(2)方程 x2-9=0的解的集合.
解:(1)由大于3小于10的整数组成的集合用列举法可表示为{4,5,6,7,8,9};
(2)方程x2-9=0的解的集合用列举法可表示为{-3,3}.
练习
例2 用描述法表示下列集合:
(1)小于10的所有有理数组成的集合;
(2)所有偶数组成的集合.
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为
解:(1)小于10的所有有理数组成的集合用描述法可表示为
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为
解:(1)小于10的所有有理数组成的集合用描述法可表示为
练习
试分别用列举法和描述法 表示下列集合:
(1)方程 的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合.
知识点5:集合的分类
空集:不含有任何元素的集合
φ
有限集:含有限个元素的集合
无限集:含无限个元素的集合
1.集合与元素的概念及关系;
3.集合元素的性质:确定性;互异性;无序性;
2.常用数集及有关符号:
4.集合的表示方法:
5.集合的分类:
