人教版数学八年级下册:19.2.2一次函数的图像 教案
文档属性
| 名称 | 人教版数学八年级下册:19.2.2一次函数的图像 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 07:22:19 | ||
图片预览




文档简介
一次函数的图像
一、课题
一次函数的图像
二、课时
一课时(40分钟)
三、教材版本
人教2011课标版部审
四、教材分析
本节是学生在学习了一次函数的概念后,进一步学习的内容。首先,教材通过y=-6x和y=-6x+5这两个函数图像的呈现,让学生观察分析它们的特点,并尝试找出他们的联系及变化;然后,教材总结出:当正比例函数y=kx与一次函数y=kx+b(其中k≠0,b≠0)的k相同时,这两个函数的图像都是一条直线且平行;直线y=kx平移?b?个单位长度(当b>0时,向上平移;当b<0时,向下平移)得到一次函数y=kx+b的图像;最后,教材通过两点法画出一次函数y=2x-1和y=-0.5x+1的图像,教材在分析图像特点的基础上,得出性质:当k>0时,y随着x的增大而增大,与b无关;当k<0时,y随着x的增大而减小,与b无关。
五、学情分析
我班共有34名藏族孩子,其中男生19名,女生14名。经过近两年的学习,孩子们已经适应了在学校的生活、学习。现在大多数孩子的汉语理解能力和交流水平都挺好;但仍有少数孩子的这些能力、水平较差,学习的交流与知识的理解存在一定障碍。
我班有4个孩子来自单亲家庭,有5个孩子属于留守儿童。这些孩子的行为习惯、学习习惯较差,自控能力也差,学习成绩不理想,是班上的学困生。八年级是初中学习的分水岭,这学期少数学困生已经明显的表现出厌学、弃学的苗头。
这部分孩子需要得到老师更多的关爱和帮助,以使他们建立恰当的学习目标,形成适合他们的学习方法,鼓励他们,督促他们,帮助他们逐步树立信心。
我多维度的评价学生,关注他们的智力表现与非智力表现。我采取分组学习的方式教学,安排基础较好的同学帮助基础较差的同学,并对帮助效果进行检测。对学困生的点滴进步都及时予以表扬。在布置作业方面,我根据学生的不同基础和水平,设计了不同难度的试题,题型分为必做题和选做题;其中必做题重在考察学生的“双基”,而选择题需要进一步思考才能做。我让他们根据自己的实际情况选择,鼓励孩子们尝试做选做题,以达到巩固和提升的目的。
六、教学目标
(一)知识与技能
1、掌握用两点法画出一次函数图像的方法,能根据k值与b值画出一次函数的大致图像,能根据函数的大致图像判断出k值、b值的大小关系;
2、能根据正比例函数y=kx的图像平移出一次函数y=kx+b的图像(其中k≠0,b≠0);
3、根据函数图像间的关系,求解其交点或k值;
4、掌握一次函数y=kx+b的图像性质(其中k≠0)。
(二)过程与方法
1、观察(1)y=-6x-5、y=-6x、y=-6x+5;(2)y=2x+1、y=2x、y=2x-1函数图像,在老师的引导下总结出它们的形状特征及特点,总结出函数图像平移的方法、两个一次函数的图像平行时k的特点、一次函数图像的六种情形;
2、根据y=2x-1和y=-2x+3的函数图像,观察出它们的交点均在这两条直线上,并通过联立二元一次方程组求解其交点坐标。
(三)情感态度价值观
体会数形结合和分类讨论的数学思想。
七、教学重难点
重点
1、用两点法画出一次函数图像;
2、根据k、b的大小,画出函数的大致图像;
3、根据两个一次函数解析式,求解其交点的坐标。
难点
1、根据一次函数图像y=kx+b1平移出y=kx+b2的图像;
2、根据函数的大致图像,判断出k、b的大小;
3、根据两个一次函数解析式,求解其交点的坐标。
八、教学方法
讲授法、小组讨论法、练习法
九、教学辅助
白板 课件 三角板 几何画板
十、教学过程
孩子们回顾之前学习过的知识:正比例函数和一次函数的图像都是一条直线,而两点确定一条直线,故可用两点确定一次函数和正比例函数的图像。
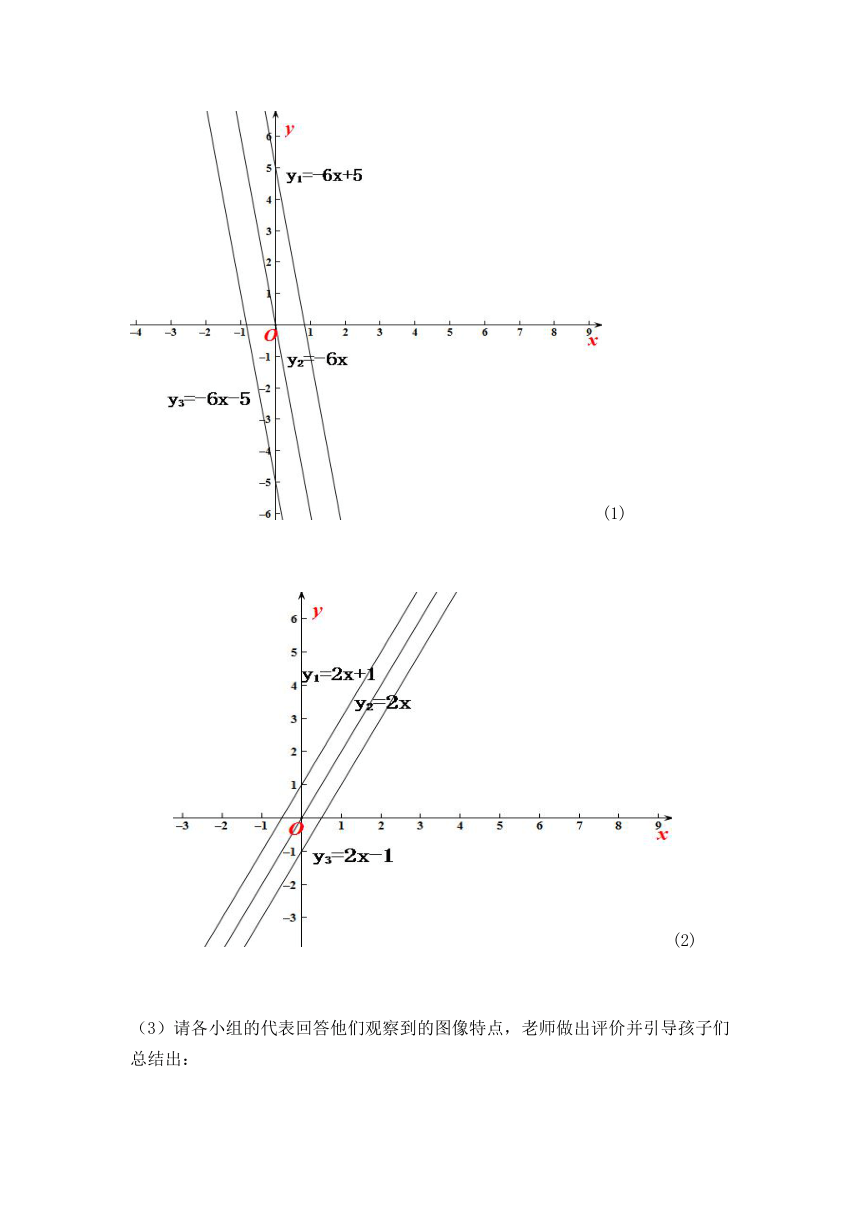
1、活动一:用两点法画出(1):y=-6x-5、y=-6x、y=-6x+5;(2):y=2x+2、y=2x、y=2x-2的函数图像
步骤:(1)老师用两点法列表、描点并用课件呈现出以上两组函数的图像;
(2)让学生先观察这两组函数图像的形状及特点,并让小组讨论这两组函数内三条直线的关系;
(1)
(2)
(3)请各小组的代表回答他们观察到的图像特点,老师做出评价并引导孩子们总结出:
a、当比例系数k1=k2时,一次函数y1=k1x+b1和y2=k2x+b2的图像平行,与b值无关;
b、y=kx向上平移b个单位得到y=kx+b(其中b>0),y=kx向下平移c个单位得到y=kx-c(其中c>0);
c、当函数图像形状像汉字笔画“撇”时,有k>0;当函数图像形状像汉字笔画“捺”时,有k<0。
分类讨论:一次函数的六种情形
一次函数 k值 b值 类型
y=kx+b k>0 b>0 情况一
b=0 情况二
b<0 情况三
k<0 b>0 情况四
b=0 情况五
b<0 情况六
小结:
a、一次函数的图像是一条直线;
b、当一次函数的图像形状是汉字笔画“撇”时,一定有比例系数k>0,函数值y随着x的增大而增大,且与b值无关;
c、当一次函数的图像形状是汉字笔画“捺”时,一定有比例系数k<0,函数值y随着x的增大而减小,且与b值无关;
d、根据图像与y轴的交点位置来判断b的大小。一次函数图像交于y轴的正半轴时,有b>0;图像交于原点时,有b=0;图像交于y轴的负半轴时,有b<0。
2、活动二:画出y=2x-1,y=-2x+3的函数图像,并讨论它们的特点
小结:当比例系数k1≠k2时,一次函数y1=k1x+b1和y2=k2x+b2的图像相交;交点P同时在两条直线上,故其坐标由二元一次方程组y1=k1x+b1和y2=k2x+b2共同决定;
3、巩固练习
(1)已知y=3x+5与y=ax-3平行,那么a=_________。
(2)一次函数y=-2x-1向_____平移______个单位得到一次函数y=-2x+1。
(3)已知一次函数y=4x+3经过第___________象限,y随着x的增大而________;y=-x-1经过第___________象限,y随着x的增大而________。
(4)已知一次函数y=kx+b经过第一、第二和第四象限,那么有k_______, b_______;y随着x的增大而_________。
(5)已知一次函数y=-x+2与y=2x+5相交于点P,则点P坐标为_______。
十一、小结
十二、作业
练习册93页第1题、第2题、第3题
十三、板书
十四、教学反思
情况一
在一次函数y=kx+b的图像中,该图像具有以下特点:
(1)k>0,b>0;
(2)图像经过第一、第二和第三象限;
(3)y随着x的增大而增大;
(4)函数的图像是一条直线,其形状如汉字的笔画“撇”,且经过y轴的上半部分,故简记为:上撇。
情况二
在正比例函数y=kx的图像中,该图像具有以下特点:
(1)k>0,b=0;
(2)图像经过第一、第三象限;
(3)y随着x的增大而增大;
(4)函数的图像是一条直线,其形状如汉字的笔画“撇”,且经过原点,故简记为:零撇;
(5)正比例函数是一个特殊的一次函数,特殊之处在于b=0。
情况三
在一次函数y=kx+b的图像中,该图像具有以下特点:
(1)k>0,b<0;
(2)图像经过第一、第三和第四象限;
(3)y随着x的增大而增大;
(4)函数的图像是一条直线,其形状如汉字的笔画“撇”,且经过y轴的下半部分,故简记为:下撇。
情况四
在一次函数y=kx+b的图像中,该图像具有以下特点:
(1)k<0,b>0;
(2)图像经过第一、第二和第四象限;
(3)y随着x的增大而减小;
(4)函数的图像是一条直线,其形状如汉字的笔画“捺”,且经过y轴的上半部分,故简记为:上捺;
(5)正比例函数是一个特殊的一次函数,特殊之处在于b=0。
情况五
在正比例函数y=kx的图像中,该图像具有以下特点:
(1)k<0,b=0;
(2)图像经过第二、第四象限;
(3)y随着x的增大而减小;
(4)函数的图像是一条直线,其形状如汉字的笔画“捺”,且经过原点,故简记为:零捺。
情况六
在一次函数y=kx+b的图像中,该图像具有以下特点:
(1)k<0,b<0;
(2)图像经过第二、第三和第四象限;
(3)y随着x的增大而减少;
(4)函数的图像是一条直线,其形状如汉字的笔画“捺”,且经过y轴的下半部分,故简记为:下捺。
一次函数的图像
2、两个一次函数图像的平行与相交
3、一次函数y=kx+b的平移
4、一次函数的图像特点
5、一次函数的性质
1、用两点法画出一次函数的图像
一次函数的图像
一、活动1 y=-6x-5、y=-6x、y=-6x+5的函数图像
二、活动2 y=2x+2、y=2x、y=2x-2的函数图像
三、习题巩固 情况1到情况6
四、小结
