人教版七年级数学上册1.2.4绝对值课件(2课时38张ppt)
文档属性
| 名称 | 人教版七年级数学上册1.2.4绝对值课件(2课时38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 09:14:33 | ||
图片预览





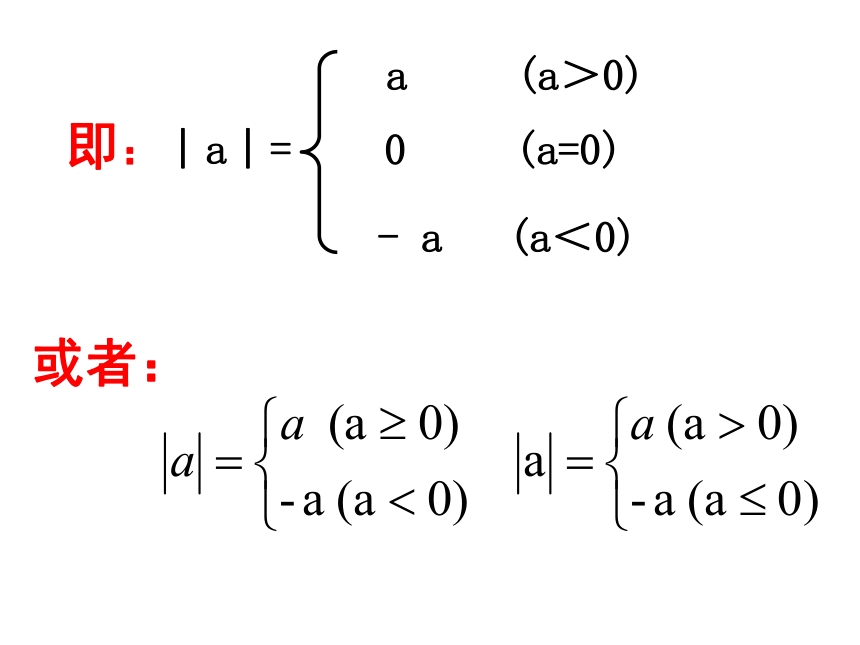





文档简介
(共38张PPT)
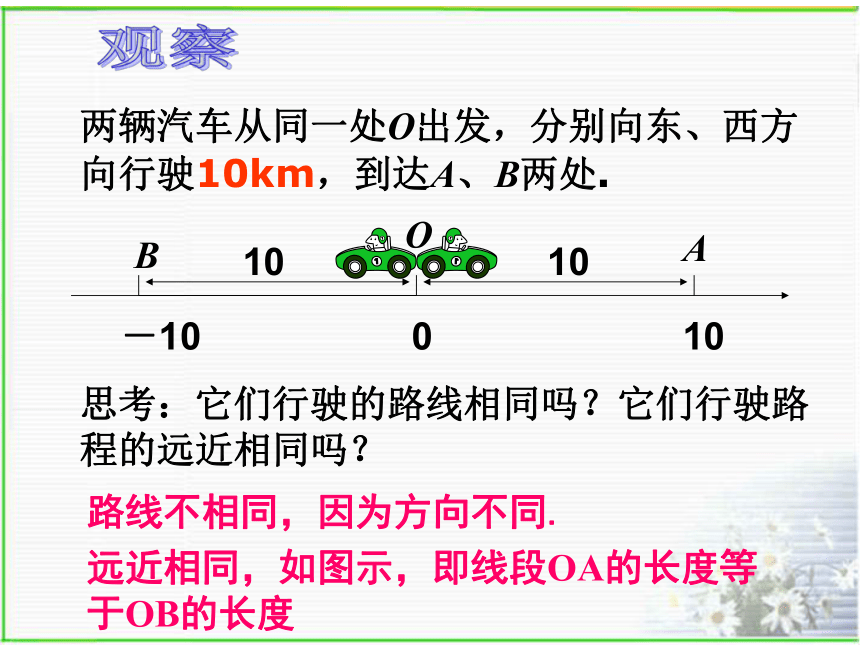
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
路线不相同,因为方向不同.
远近相同,如图示,即线段OA的长度等于OB的长度
O
B
A
0
10
-10
10
10
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a| 。
想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数、负数和0
例如,A,B两点分别表示10和-10,它们与原点的距离都是10个单位长度,所以10和-10的绝对值都是10,即|10|=10, |-10|=10,显然|0|=0.
想一想 互为相反数的两个数的绝对值有什么关系?
相等
做一做
写出下列各数的绝对值:
解:
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(3)如果a=0,那么|a|=______
(2)如果a<0,那么|a|=______
(1)如果a>0,那么|a|=______
a
-a
0
a (a>0)
0 (a=0)
- a (a<0)
即:︱a︱=
或者:
即:
正数或0
让我们来认识
1、说出下列各式的值
2、求下列各数的绝对值
6 , -3.9 , 0, ,3b(b<0)
3、判断下列说法是否正确:
(1)符号相反的数互为相反数 ( )
(2)符号相反且绝对值相等的数互为相反数( )
(3)一个数的绝对值越大,表示它的点在数轴上越靠右 ( )
(4)一个数的绝对值越大,表示它的点在数轴上离原点越远 ( )
×
√
×
√
(5)当a≠0时,|a|总是大于0 ( )
√
(7)-1.4<0,则│-1.4│<0 ( ) (8)│-32︱的相反数是32 ( )
×
×
4、已知︱x︱=|2| ,︱-y︱=3,
则x=____;y =_______ 。
5、绝对值等于本身的数一定是 ____ _ ,绝对值等于相反数的数一定是 _____ 。
_2或-2
3或-3
非负数
非正数
6、
满足︱x︱≤3的所有整数是__________________________。
±3,±2,±1,0
7.下列说法正确的是_____。(填序号)
①若m=n,则 ;②若m=-n,则 ;③若 ,则m=n;④若 ,则m=-n
①②
8.
设a是最小的自然数,b是绝对值最小的数,c是相反数等于它本身的数,则a+b+c= .
0
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、任何一个有理数的绝对值
都是非负数。
3、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
第二课时
小学时学过比较数的大小吗?怎样比较的?
通分后根据同分母比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
在数轴上表示的两个数,右边的数总比左边的数大.
小 大
有理数大小的比较方法:
负数
0
正数
<
<
观察下列数,你会比较他们的大小吗?
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5____-7
-2_____0
2_____0
?
?
?
?
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
例:比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
(3)将数在数轴上表示,按从左到右的顺序排列,即是数从小到大的顺序.
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大小吗?
>
>
<
>
1. 用“<”,“>”,“=”连接
3___-4; 5___0;
-7 ___0; -3 ___-|-3|;
-|-7| ___0; |2| ___-2.
<
>
=
>
>
<
2. 完成 P13页练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2.如果一个数的绝对值等于4.53 ,则这个数是_______________.
3.如果a 的相反数是-0.86,那么
|a| =______.
4.53或-4.53
3或-1
0.86
4.如果|x-1|=2,则x=__________.
5.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
6.若|a|+ |b-3| =0.则a =_____, b= _____.
3
0
解:先化简
|5|=5,-(-4)=4 ,-|-5|= -5
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、任何一个有理数的绝对值
都是非负数。
3、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
4.有理数大小比较方法:
(1)负数<0,0<正数,负数<正数;
(2)两负数相比较,绝对值大的反而小;
(3)将数在数轴上表示,按从左到右的顺序排列,即是数从小到大的顺序.
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2、计算:
1、180+(-10)
2、(-10)+(-1)
3、45+(-45)
4、(-23)+0
5、(-25)+(-7)
6、(-13)+5
7、(-1/2)+(+1/3)
8、2/3 +(-3/5)
9、(-0.9)+1.5
10、2.7+(-3.5)
=170
=-11
=0
=-23
=-32
=-8
=-1/6
=1/15
=0.6
=-0.8
3.如果一个数的绝对值等于4.53 ,则这个数是_______________.
4.如果a 的相反数是-0.86,那么
|a| =______.
4.53或-4.53
3或-1
0.86
5.如果|x-1|=2,则x=__________.
6.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
7.若|a|+ |b-3| =0.则a =_____, b= _____.
3
0
解:先化简
|5|=5,-(-4)=4 ,-|-5|= -5
1.已知x>4,则|x-3|+ |4-x|.
解: 因为 x>4,
所以x-3>0, 4-x<0,
所以|x-3|+ |4-x|=x-2+(x-4)
=2x-6.
思考题
2.已知|x-4| + |1-y| =0,求3x+4y 的值.
解: 因为 |x-4| + |1-y| =0,
所以 x-4=0, 1-y=0.
所以 x=4, y=1.
所以 3x+4y =3×4+4×1=16.
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
路线不相同,因为方向不同.
远近相同,如图示,即线段OA的长度等于OB的长度
O
B
A
0
10
-10
10
10
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a| 。
想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数、负数和0
例如,A,B两点分别表示10和-10,它们与原点的距离都是10个单位长度,所以10和-10的绝对值都是10,即|10|=10, |-10|=10,显然|0|=0.
想一想 互为相反数的两个数的绝对值有什么关系?
相等
做一做
写出下列各数的绝对值:
解:
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(3)如果a=0,那么|a|=______
(2)如果a<0,那么|a|=______
(1)如果a>0,那么|a|=______
a
-a
0
a (a>0)
0 (a=0)
- a (a<0)
即:︱a︱=
或者:
即:
正数或0
让我们来认识
1、说出下列各式的值
2、求下列各数的绝对值
6 , -3.9 , 0, ,3b(b<0)
3、判断下列说法是否正确:
(1)符号相反的数互为相反数 ( )
(2)符号相反且绝对值相等的数互为相反数( )
(3)一个数的绝对值越大,表示它的点在数轴上越靠右 ( )
(4)一个数的绝对值越大,表示它的点在数轴上离原点越远 ( )
×
√
×
√
(5)当a≠0时,|a|总是大于0 ( )
√
(7)-1.4<0,则│-1.4│<0 ( ) (8)│-32︱的相反数是32 ( )
×
×
4、已知︱x︱=|2| ,︱-y︱=3,
则x=____;y =_______ 。
5、绝对值等于本身的数一定是 ____ _ ,绝对值等于相反数的数一定是 _____ 。
_2或-2
3或-3
非负数
非正数
6、
满足︱x︱≤3的所有整数是__________________________。
±3,±2,±1,0
7.下列说法正确的是_____。(填序号)
①若m=n,则 ;②若m=-n,则 ;③若 ,则m=n;④若 ,则m=-n
①②
8.
设a是最小的自然数,b是绝对值最小的数,c是相反数等于它本身的数,则a+b+c= .
0
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、任何一个有理数的绝对值
都是非负数。
3、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
第二课时
小学时学过比较数的大小吗?怎样比较的?
通分后根据同分母比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
在数轴上表示的两个数,右边的数总比左边的数大.
小 大
有理数大小的比较方法:
负数
0
正数
<
<
观察下列数,你会比较他们的大小吗?
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5____-7
-2_____0
2_____0
?
?
?
?
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
例:比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
(3)将数在数轴上表示,按从左到右的顺序排列,即是数从小到大的顺序.
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大小吗?
>
>
<
>
1. 用“<”,“>”,“=”连接
3___-4; 5___0;
-7 ___0; -3 ___-|-3|;
-|-7| ___0; |2| ___-2.
<
>
=
>
>
<
2. 完成 P13页练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2.如果一个数的绝对值等于4.53 ,则这个数是_______________.
3.如果a 的相反数是-0.86,那么
|a| =______.
4.53或-4.53
3或-1
0.86
4.如果|x-1|=2,则x=__________.
5.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
6.若|a|+ |b-3| =0.则a =_____, b= _____.
3
0
解:先化简
|5|=5,-(-4)=4 ,-|-5|= -5
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、任何一个有理数的绝对值
都是非负数。
3、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
4.有理数大小比较方法:
(1)负数<0,0<正数,负数<正数;
(2)两负数相比较,绝对值大的反而小;
(3)将数在数轴上表示,按从左到右的顺序排列,即是数从小到大的顺序.
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2、计算:
1、180+(-10)
2、(-10)+(-1)
3、45+(-45)
4、(-23)+0
5、(-25)+(-7)
6、(-13)+5
7、(-1/2)+(+1/3)
8、2/3 +(-3/5)
9、(-0.9)+1.5
10、2.7+(-3.5)
=170
=-11
=0
=-23
=-32
=-8
=-1/6
=1/15
=0.6
=-0.8
3.如果一个数的绝对值等于4.53 ,则这个数是_______________.
4.如果a 的相反数是-0.86,那么
|a| =______.
4.53或-4.53
3或-1
0.86
5.如果|x-1|=2,则x=__________.
6.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
7.若|a|+ |b-3| =0.则a =_____, b= _____.
3
0
解:先化简
|5|=5,-(-4)=4 ,-|-5|= -5
1.已知x>4,则|x-3|+ |4-x|.
解: 因为 x>4,
所以x-3>0, 4-x<0,
所以|x-3|+ |4-x|=x-2+(x-4)
=2x-6.
思考题
2.已知|x-4| + |1-y| =0,求3x+4y 的值.
解: 因为 |x-4| + |1-y| =0,
所以 x-4=0, 1-y=0.
所以 x=4, y=1.
所以 3x+4y =3×4+4×1=16.
