高中数学人教版必修5课件:2.6数列的三个特殊问题(共20张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:2.6数列的三个特殊问题(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 15:10:04 | ||
图片预览






文档简介
(共20张PPT)
数列
1.定义与基本概率
2.两个特殊数列
3.三个特殊问题
递推公式
通项公式
前n项和
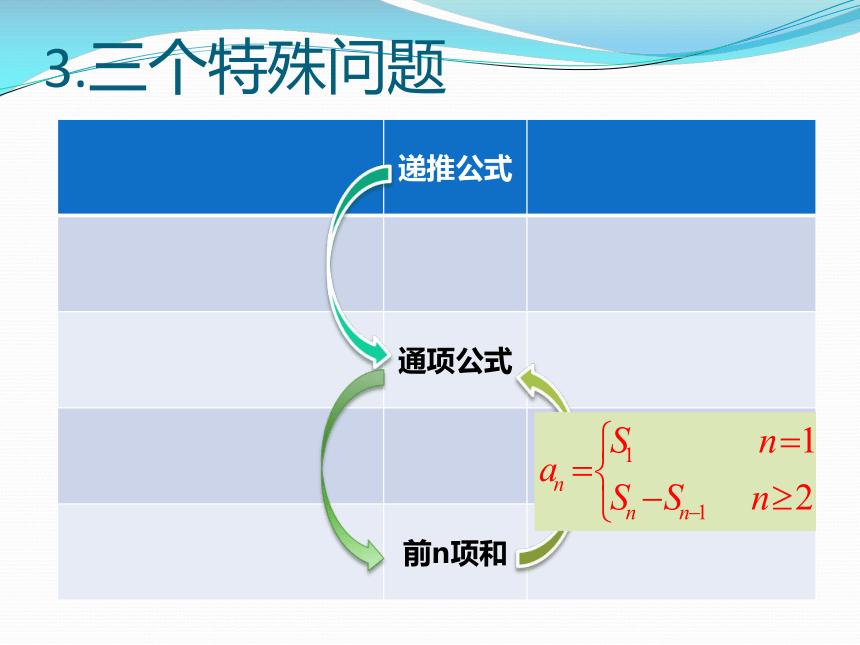
3.三个特殊问题
当n=1时:
当n>=2时:
将n=1代入上式验首项
或
3.三个特殊问题1:和求通项
(2011·四川文,9)数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则a6=
当n=1时:
当n>=2时:
将n=2代入上式可验递推从第2项起适用,所以进一步验证
当n=1时:
当n>=2时:
将n=1代入上式验首项
或
当n=1时:
当n>=2时:
将n=2代入上式可验
递推从第?项起适用,从而可背通项为:
其他 递推公式
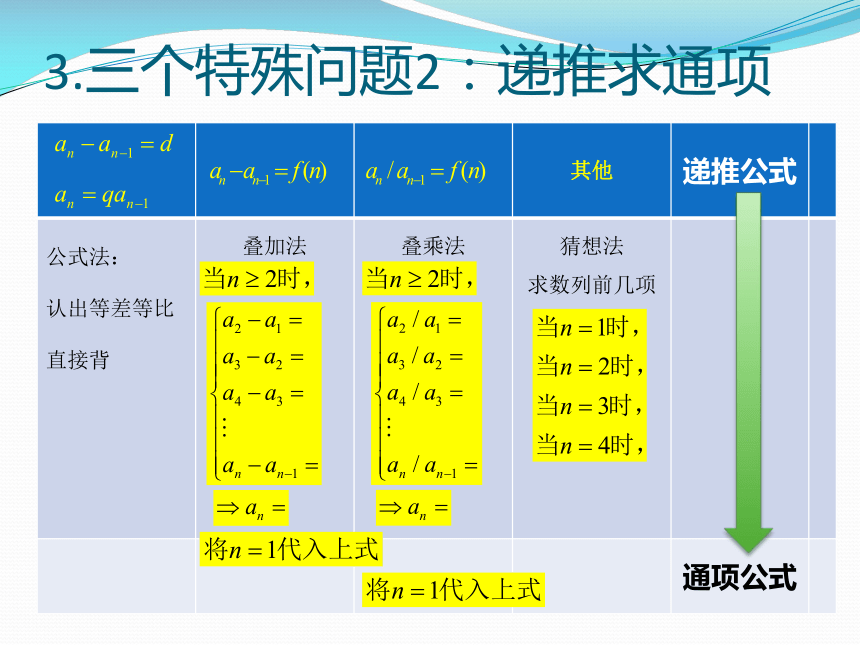
公式法:
认出等差等比直接背 叠加法
叠乘法
猜想法
求数列前几项
通项公式
3.三个特殊问题2:递推求通项
通项公式
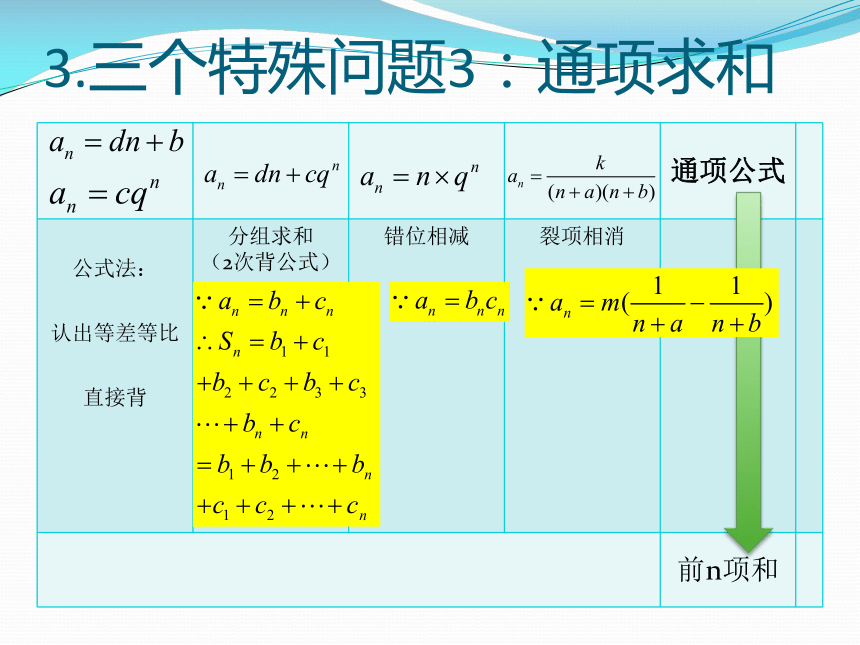
公式法:
认出等差等比直接背
分组求和
(2次背公式) 错位相减 裂项相消
前n项和
3.三个特殊问题3:通项求和
若{bn}是等差数列,{cn}是公比为q(q≠1)的等比数列,an=bn + cn,则数列{an}求和时,用分组求和法
错位相减法适用于下面的数列求和情况:
{bn}是等差数列,{cn}是公比为q(q≠1)的等比数列,an=bn×cn则数列{an}求和时,用错位相减法
Sn=b1c1+b2c2+b3c3+…+bncn
qSn= b1c2+b2c3+b3c4+…+bncn+1
Sn-qSn=b1c1-bncn+1 +dc2+dc3+…+dcn
=b1c1-bncn+1+d(c2+c3+…+cn)
∵{cn}为等比数列,故c2+c3+…+cn与cn+1均可求,又{bn}是等差数列∴bn可求,从而可得Sn.
其他 递推公式
公式法 叠加法
叠乘法
猜想法
代入求前几项
通项公式
公式法 分组求和
(2次背公式) 错位相减 裂项相消
前n项和
3.三个特殊问题
三步走
递推公式
通项公式
前n项和
3.三个特殊问题
当n=1时:
当n>=1时:
数列
1.定义与基本概率
2.两个特殊数列
3.三个特殊问题
递推公式
通项公式
前n项和
3.三个特殊问题
当n=1时:
当n>=2时:
将n=1代入上式验首项
或
3.三个特殊问题1:和求通项
(2011·四川文,9)数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则a6=
当n=1时:
当n>=2时:
将n=2代入上式可验递推从第2项起适用,所以进一步验证
当n=1时:
当n>=2时:
将n=1代入上式验首项
或
当n=1时:
当n>=2时:
将n=2代入上式可验
递推从第?项起适用,从而可背通项为:
其他 递推公式
公式法:
认出等差等比直接背 叠加法
叠乘法
猜想法
求数列前几项
通项公式
3.三个特殊问题2:递推求通项
通项公式
公式法:
认出等差等比直接背
分组求和
(2次背公式) 错位相减 裂项相消
前n项和
3.三个特殊问题3:通项求和
若{bn}是等差数列,{cn}是公比为q(q≠1)的等比数列,an=bn + cn,则数列{an}求和时,用分组求和法
错位相减法适用于下面的数列求和情况:
{bn}是等差数列,{cn}是公比为q(q≠1)的等比数列,an=bn×cn则数列{an}求和时,用错位相减法
Sn=b1c1+b2c2+b3c3+…+bncn
qSn= b1c2+b2c3+b3c4+…+bncn+1
Sn-qSn=b1c1-bncn+1 +dc2+dc3+…+dcn
=b1c1-bncn+1+d(c2+c3+…+cn)
∵{cn}为等比数列,故c2+c3+…+cn与cn+1均可求,又{bn}是等差数列∴bn可求,从而可得Sn.
其他 递推公式
公式法 叠加法
叠乘法
猜想法
代入求前几项
通项公式
公式法 分组求和
(2次背公式) 错位相减 裂项相消
前n项和
3.三个特殊问题
三步走
递推公式
通项公式
前n项和
3.三个特殊问题
当n=1时:
当n>=1时:
