24.2.3 圆心角、弧、弦、弦心距之间的关系(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.2.3 圆心角、弧、弦、弦心距之间的关系(基础达标+巩固提升+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 00:00:00 | ||
图片预览

文档简介
沪科版数学九年级下册同步课时训练
第24章 圆
24.2 圆的基本性质
第3课时 圆心角、弧、弦、弦心距间关系
要点测评 基础达标
要点1 圆心角、弧、弦、弦心距间关系
1. 下列命题中正确的是( )
A. 相等的圆心角所对的弦相等 B. 两条弦相等,它们所对的弧也相等
C. 相等的弦的弦心距相等 D. 相等的弧所对的弦相等
2. 已知圆O的半径长为6,若弦AB=6,则弦AB所对的圆心角等于 .
3. 如图所示,以?ABCD的顶点A为圆心,AB为半径作☉A,分别交AD,BC于点E,F,延长BA交☉A于点G,求证:=.
要点2 圆心角、弧、弦、弦心距间关系在推理证明中的应用
4. 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.则的度数为 .
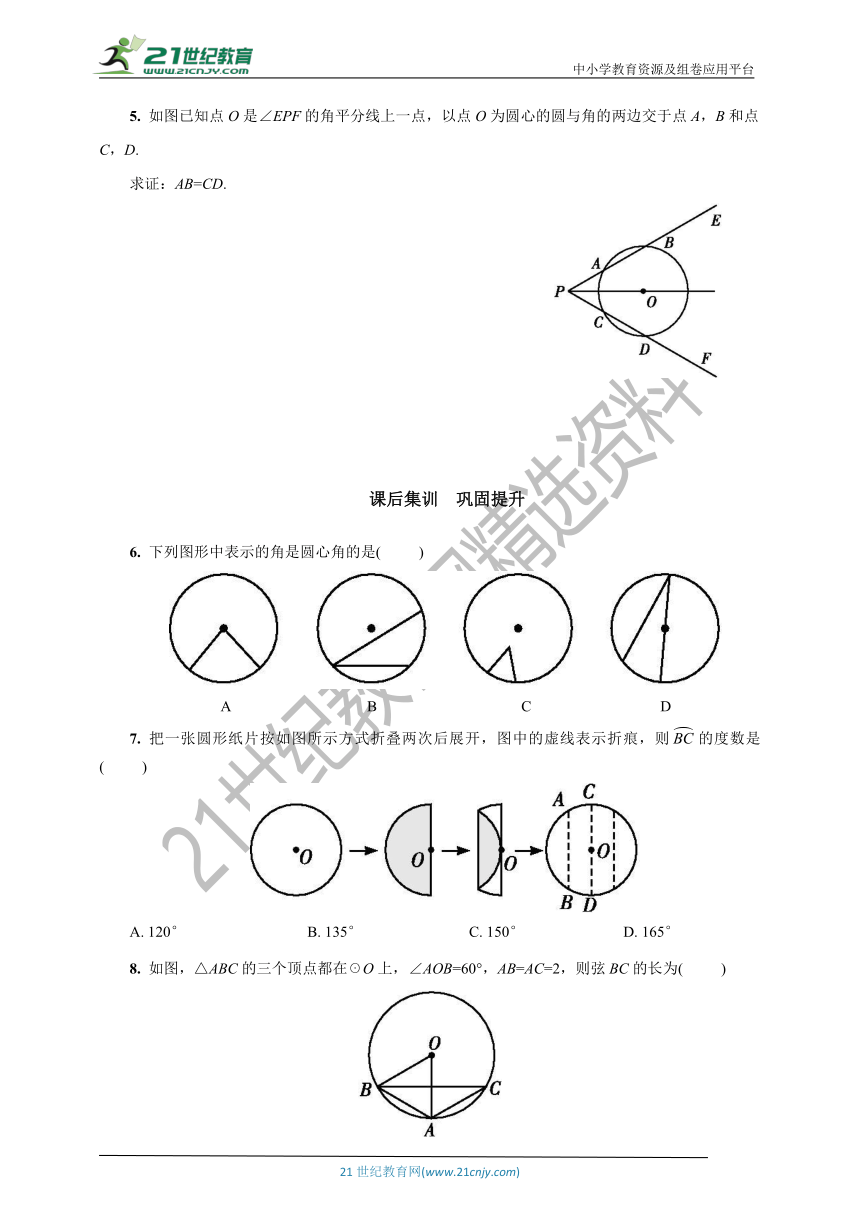
5. 如图已知点O是∠EPF的角平分线上一点,以点O为圆心的圆与角的两边交于点A,B和点C,D.
求证:AB=CD.
课后集训 巩固提升
6. 下列图形中表示的角是圆心角的是( )
A B C D
7. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A. 120° B. 135° C. 150° D. 165°
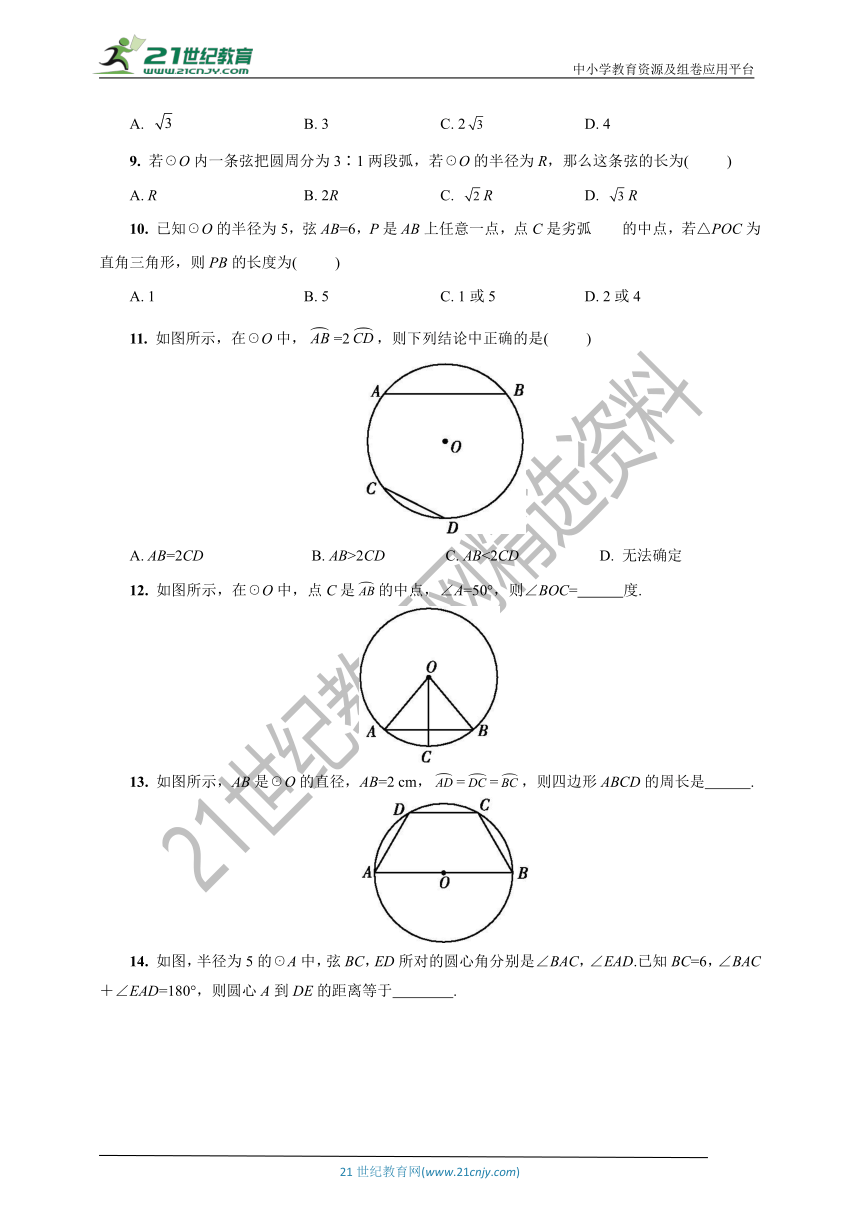
8. 如图,△ABC的三个顶点都在☉O上,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B. 3 C. 2 D. 4
9. 若☉O内一条弦把圆周分为3∶1两段弧,若☉O的半径为R,那么这条弦的长为( )
A. R B. 2R C. R D. R
10. 已知☉O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧 的中点,若△POC为直角三角形,则PB的长度为( )
A. 1 B. 5 C. 1或5 D. 2或4
11. 如图所示,在☉O中,=2,则下列结论中正确的是( )
A. AB=2CD B. AB>2CD C. AB<2CD D. 无法确定
12. 如图所示,在☉O中,点C是的中点,∠A=50°,则∠BOC= 度.?
13. 如图所示,AB是☉O的直径,AB=2 cm,==,则四边形ABCD的周长是 .?
14. 如图,半径为5的☉A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知BC=6,∠BAC+∠EAD=180°,则圆心A到DE的距离等于 .?
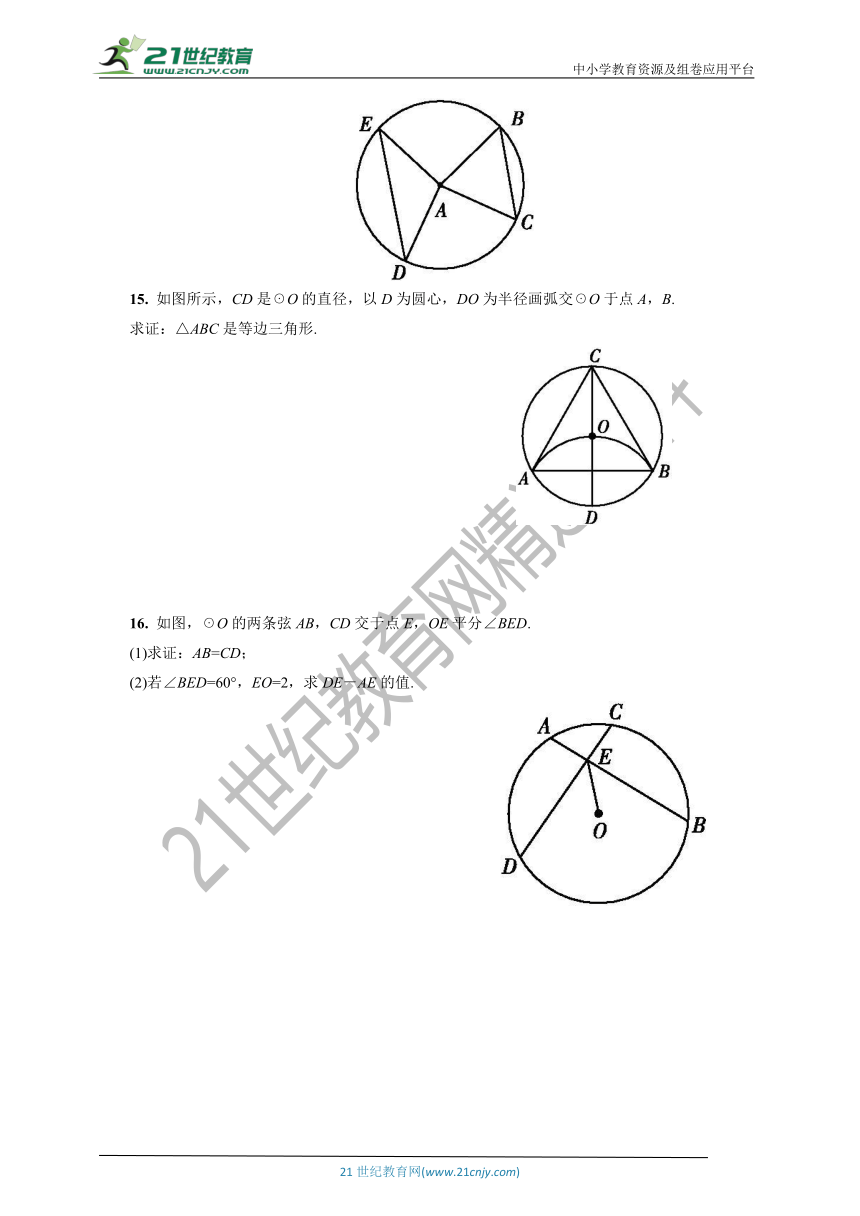
15. 如图所示,CD是☉O的直径,以D为圆心,DO为半径画弧交☉O于点A,B.
求证:△ABC是等边三角形.
16. 如图,☉O的两条弦AB,CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE-AE的值.
参 考 答 案
1. D 【解析】各组量做条件出现时,必须限定在同圆或等圆中,但“弧”可以除外,因为等弧指的是在同圆或等圆中,能够互相重合的弧,故选D.
2. 120° 【解析】作OC⊥AB于C,连接OA,OB,则AC=BC=AB=3,OC==3,所以OC=OA,所以∠A=30°,所以∠AOB=180°-30°-30°=120°,所以弦AB所对的圆心角的度数为120°.
3. 证明:如图.连接AF,因为四边形ABCD是平行四边形,所以AD∥BC,所以∠GAE=∠B,∠EAF=∠AFB.又因为AB=AF,所以∠B=∠AFB,所以∠GAE=∠EAF,所以=.
4. 34° 【解析】连接CD,因为∠C=90°,∠B=28°,所以∠A=62°,因为CA=CD,所以∠CDA=∠A=62°,所以∠ACD=56°,所以∠DCE=90°-56°=34°,所以的度数为34°.
5. 证明:作OG⊥AB于G,OH⊥CD于H,因为OP为∠EPF的平分线,所以∠OPG=∠OPH,在Rt△POG和Rt△POH中,∠OPG=∠OPH,OP=OP,∠PGO=∠PHO,所以Rt△POG≌Rt△POH,所以OG=OH,所以AB=CD.
6. A
7. C 【解析】如图所示,连接BO,过点O作OE⊥AB于点E,由题意可得:EO=BO,AB∥DC,可得∠EBO=30°,故∠BOD=30°,则∠BOC=150°,故的度数是150°,故选C.
8. C 【解析】如图,设AO与BC交于点D.因为∠AOB=60°,OB=OA,所以△OAB是等边三角形,所以∠BAO=60°,即∠BAD=60°.又因为AB=AC,所以=,所以AD⊥BC,所以BD=CD,所以在Rt△ABD中,BD=AB·sin 60°=2×=,所以BC=2BD=2.故选C.
9. C 【解析】如图所示,因为弦AB把圆周分成3∶1两段弧,所以是圆周的,所以∠AOB=360°×=90°,在Rt△AOB中由勾股定理得AB==R.故选C.
10. C 【解析】如图,因为点C是劣弧的中点,所以OC垂直平分AB,所以DA=DB=3,所以OD=4,CD=1,若△POC为直角三角形,只能是∠OPC=90°,则△POD∽△CPD,所以=,所以PD2=4×1=4,所以PD=2,所以当P在OC的右侧时,PB=3-2=1,当P在OC的左侧时,PB=3+2=5,所以PB的长度为1或5,故选C.
11. C 【解析】如图所示,取的中点E,连接AE,BE.因为=2,==,所以==,所以CD=AE=BE,在△ABE中,AE+BE>AB,即2CD>AB.故选C.
12. 40 【解析】因为=,所以∠AOC=∠BOC.又因为OA=OB,∠A=50°,所以∠A=∠B=50°,所以∠BOC=(180°-2×50°)=40°.
13. 5 cm 【解析】如图所示,连接OC,OD.因为==,所以∠AOD=∠DOC=∠COB=60°.又因为OA=OD=OC=OB,所以△OAD,△ODC,△OBC都是等边三角形,所以AD=CD=CB=OA=OB=1 cm,所以AB+BC+CD+DA=5 cm.
14. 3 【解析】作AH⊥DE于H,作直径EF,连接DF,如图,因为∠BAC+∠EAD=180°,所以∠BAC=∠DAF,所以BC=DF=6,因为AH⊥DE,所以EH=DH,因为EA=AF,所以AH=DF=3,所以圆心A到DE的距离等于3.
15. 证明:连接OA,AD,DB,OB.因为OA=OB=OD=AD=BD,所以△OAD和△OBD是等边三角形.所以∠AOD=∠DOB=60°,所以∠AOB=120°,∠AOC=∠BOC=120°,所以∠AOB=∠AOC=∠BOC,所以AB=AC=BC,所以△ABC是等边三角形.
16. (1)证明:过点O作AB,CD的垂线,垂足为M,N,因为OE平分∠BED,且OM⊥AB,ON⊥CD,所以OM=ON,所以AB=CD.
(2)解:由(1)知OM=ON,AB=CD,OM⊥AB,ON⊥CD,所以DN=CN=AM=BM,在Rt△EON与Rt△EOM中,因为所以Rt△EON≌Rt△EOM,所以NE=ME,所以CD-DN-NE=AB-BM-ME,即AE=CE,所以DE-AE=DE-CE=DN+NE-CE=CN+NE-CE=2NE,因为∠BED=60°,OE平分∠BED,所以∠NEO=∠BED=30°,所以ON=OE=1,在Rt△EON中,由勾股定理得NE==,所以DE-AE=2NE=2.
第24章 圆
24.2 圆的基本性质
第3课时 圆心角、弧、弦、弦心距间关系
要点测评 基础达标
要点1 圆心角、弧、弦、弦心距间关系
1. 下列命题中正确的是( )
A. 相等的圆心角所对的弦相等 B. 两条弦相等,它们所对的弧也相等
C. 相等的弦的弦心距相等 D. 相等的弧所对的弦相等
2. 已知圆O的半径长为6,若弦AB=6,则弦AB所对的圆心角等于 .
3. 如图所示,以?ABCD的顶点A为圆心,AB为半径作☉A,分别交AD,BC于点E,F,延长BA交☉A于点G,求证:=.
要点2 圆心角、弧、弦、弦心距间关系在推理证明中的应用
4. 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.则的度数为 .
5. 如图已知点O是∠EPF的角平分线上一点,以点O为圆心的圆与角的两边交于点A,B和点C,D.
求证:AB=CD.
课后集训 巩固提升
6. 下列图形中表示的角是圆心角的是( )
A B C D
7. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A. 120° B. 135° C. 150° D. 165°
8. 如图,△ABC的三个顶点都在☉O上,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B. 3 C. 2 D. 4
9. 若☉O内一条弦把圆周分为3∶1两段弧,若☉O的半径为R,那么这条弦的长为( )
A. R B. 2R C. R D. R
10. 已知☉O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧 的中点,若△POC为直角三角形,则PB的长度为( )
A. 1 B. 5 C. 1或5 D. 2或4
11. 如图所示,在☉O中,=2,则下列结论中正确的是( )
A. AB=2CD B. AB>2CD C. AB<2CD D. 无法确定
12. 如图所示,在☉O中,点C是的中点,∠A=50°,则∠BOC= 度.?
13. 如图所示,AB是☉O的直径,AB=2 cm,==,则四边形ABCD的周长是 .?
14. 如图,半径为5的☉A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知BC=6,∠BAC+∠EAD=180°,则圆心A到DE的距离等于 .?
15. 如图所示,CD是☉O的直径,以D为圆心,DO为半径画弧交☉O于点A,B.
求证:△ABC是等边三角形.
16. 如图,☉O的两条弦AB,CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE-AE的值.
参 考 答 案
1. D 【解析】各组量做条件出现时,必须限定在同圆或等圆中,但“弧”可以除外,因为等弧指的是在同圆或等圆中,能够互相重合的弧,故选D.
2. 120° 【解析】作OC⊥AB于C,连接OA,OB,则AC=BC=AB=3,OC==3,所以OC=OA,所以∠A=30°,所以∠AOB=180°-30°-30°=120°,所以弦AB所对的圆心角的度数为120°.
3. 证明:如图.连接AF,因为四边形ABCD是平行四边形,所以AD∥BC,所以∠GAE=∠B,∠EAF=∠AFB.又因为AB=AF,所以∠B=∠AFB,所以∠GAE=∠EAF,所以=.
4. 34° 【解析】连接CD,因为∠C=90°,∠B=28°,所以∠A=62°,因为CA=CD,所以∠CDA=∠A=62°,所以∠ACD=56°,所以∠DCE=90°-56°=34°,所以的度数为34°.
5. 证明:作OG⊥AB于G,OH⊥CD于H,因为OP为∠EPF的平分线,所以∠OPG=∠OPH,在Rt△POG和Rt△POH中,∠OPG=∠OPH,OP=OP,∠PGO=∠PHO,所以Rt△POG≌Rt△POH,所以OG=OH,所以AB=CD.
6. A
7. C 【解析】如图所示,连接BO,过点O作OE⊥AB于点E,由题意可得:EO=BO,AB∥DC,可得∠EBO=30°,故∠BOD=30°,则∠BOC=150°,故的度数是150°,故选C.
8. C 【解析】如图,设AO与BC交于点D.因为∠AOB=60°,OB=OA,所以△OAB是等边三角形,所以∠BAO=60°,即∠BAD=60°.又因为AB=AC,所以=,所以AD⊥BC,所以BD=CD,所以在Rt△ABD中,BD=AB·sin 60°=2×=,所以BC=2BD=2.故选C.
9. C 【解析】如图所示,因为弦AB把圆周分成3∶1两段弧,所以是圆周的,所以∠AOB=360°×=90°,在Rt△AOB中由勾股定理得AB==R.故选C.
10. C 【解析】如图,因为点C是劣弧的中点,所以OC垂直平分AB,所以DA=DB=3,所以OD=4,CD=1,若△POC为直角三角形,只能是∠OPC=90°,则△POD∽△CPD,所以=,所以PD2=4×1=4,所以PD=2,所以当P在OC的右侧时,PB=3-2=1,当P在OC的左侧时,PB=3+2=5,所以PB的长度为1或5,故选C.
11. C 【解析】如图所示,取的中点E,连接AE,BE.因为=2,==,所以==,所以CD=AE=BE,在△ABE中,AE+BE>AB,即2CD>AB.故选C.
12. 40 【解析】因为=,所以∠AOC=∠BOC.又因为OA=OB,∠A=50°,所以∠A=∠B=50°,所以∠BOC=(180°-2×50°)=40°.
13. 5 cm 【解析】如图所示,连接OC,OD.因为==,所以∠AOD=∠DOC=∠COB=60°.又因为OA=OD=OC=OB,所以△OAD,△ODC,△OBC都是等边三角形,所以AD=CD=CB=OA=OB=1 cm,所以AB+BC+CD+DA=5 cm.
14. 3 【解析】作AH⊥DE于H,作直径EF,连接DF,如图,因为∠BAC+∠EAD=180°,所以∠BAC=∠DAF,所以BC=DF=6,因为AH⊥DE,所以EH=DH,因为EA=AF,所以AH=DF=3,所以圆心A到DE的距离等于3.
15. 证明:连接OA,AD,DB,OB.因为OA=OB=OD=AD=BD,所以△OAD和△OBD是等边三角形.所以∠AOD=∠DOB=60°,所以∠AOB=120°,∠AOC=∠BOC=120°,所以∠AOB=∠AOC=∠BOC,所以AB=AC=BC,所以△ABC是等边三角形.
16. (1)证明:过点O作AB,CD的垂线,垂足为M,N,因为OE平分∠BED,且OM⊥AB,ON⊥CD,所以OM=ON,所以AB=CD.
(2)解:由(1)知OM=ON,AB=CD,OM⊥AB,ON⊥CD,所以DN=CN=AM=BM,在Rt△EON与Rt△EOM中,因为所以Rt△EON≌Rt△EOM,所以NE=ME,所以CD-DN-NE=AB-BM-ME,即AE=CE,所以DE-AE=DE-CE=DN+NE-CE=CN+NE-CE=2NE,因为∠BED=60°,OE平分∠BED,所以∠NEO=∠BED=30°,所以ON=OE=1,在Rt△EON中,由勾股定理得NE==,所以DE-AE=2NE=2.
