高中数学人教版必修5课件:3.4基本不等式(共29张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:3.4基本不等式(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 700.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 00:00:00 | ||
图片预览




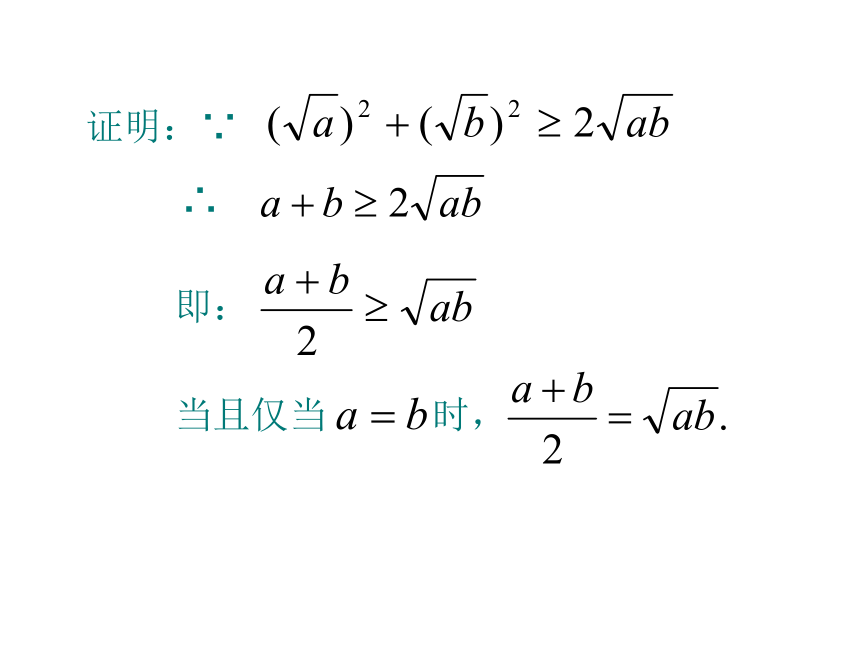



文档简介
(共29张PPT)
3.4 基本不等式
学习目标:
1、知道什么是基本不等式及其推导过程
2、会用基本不等式解决简单的问题
R
R+
(1)两个不等式的适用范围不同,
而等号成立的条件相同
(1)函数的解析式中,各项均为正数;
(2)函数的解析式中,含变数的各项的和或积必须有一个为定值;
(3)函数的解析式中,含变数的各项均相等,取得最值。
即用均值不等式求某些函数的最值时,应具备三个条件:一正二定三相等。
不正
不定
不等
×
√
×
×
×
练习1:
不正
不正
不等
分析:本题的解答忽略了对基本不等式使
用时必须是正数这一点注意事项。
分析:本题的解答在使用基本不等式时没有找到定值条件,
只是盲目的套用基本不等式的形式,导致所得结果并不是
最小的值。注意:在使用基本不等式求最值为题时,式中
的积或和必须是定值。
大
家
来
挑
错
!
大家来挑错!
解答是错误的,原因是,当x<0时,就不能运用公式.
事实上,当x<0时,y<0,故最小值不可能为2.
此时,函数的值域为(-∞,-2]∪[2,+∞).?
大家来挑错!
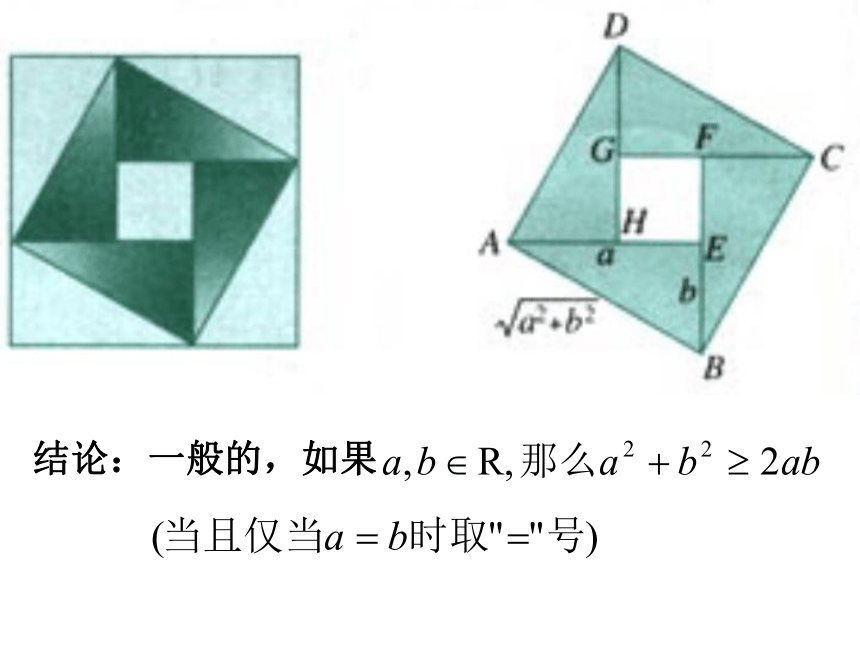
不等式2:
可变形为:
推广:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
推广:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
和定积最大,积定和最小
归纳:见和想积,乘积为定值,则和有最小值。
例3:
归纳:见积想和,和为定值,则乘积有最大值。
变式1:
A
例题讲解
例1 已知x、y都是正数,求证:
(2)(x+y)(x2+y2)(x3+y3)≥ 8x3y3。
随堂练习
1、已知a、b、c都是正数,
求证:(a+b)(b+c)(c+a)≥ 8abc。
变式、已知a、b、c都是正数,a + b + c = 1,
求证:(1 – a)(1 – b)(1 – c)≥ 8abc。
2、证明:a2+b2+c2≥ ab + bc + ca。
变式:已知a、b、c都是正数,证明:
1.凑项
:使积成为定值
4
5
1
32
2.凑系数
:使和成为定值
3.分离法
9
2
1
4.关于“1”的灵活运用
变式:
16
16
例:已知lgx+lgy=1, 的最小值是______.
2
5.基本不等式与对数相结合
2
几种利用基本不等式求最值的技巧:
2.凑系数
1.凑项
3.分离
4.“1”的妙用
小结:
作业:
3.4 基本不等式
学习目标:
1、知道什么是基本不等式及其推导过程
2、会用基本不等式解决简单的问题
R
R+
(1)两个不等式的适用范围不同,
而等号成立的条件相同
(1)函数的解析式中,各项均为正数;
(2)函数的解析式中,含变数的各项的和或积必须有一个为定值;
(3)函数的解析式中,含变数的各项均相等,取得最值。
即用均值不等式求某些函数的最值时,应具备三个条件:一正二定三相等。
不正
不定
不等
×
√
×
×
×
练习1:
不正
不正
不等
分析:本题的解答忽略了对基本不等式使
用时必须是正数这一点注意事项。
分析:本题的解答在使用基本不等式时没有找到定值条件,
只是盲目的套用基本不等式的形式,导致所得结果并不是
最小的值。注意:在使用基本不等式求最值为题时,式中
的积或和必须是定值。
大
家
来
挑
错
!
大家来挑错!
解答是错误的,原因是,当x<0时,就不能运用公式.
事实上,当x<0时,y<0,故最小值不可能为2.
此时,函数的值域为(-∞,-2]∪[2,+∞).?
大家来挑错!
不等式2:
可变形为:
推广:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
推广:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
和定积最大,积定和最小
归纳:见和想积,乘积为定值,则和有最小值。
例3:
归纳:见积想和,和为定值,则乘积有最大值。
变式1:
A
例题讲解
例1 已知x、y都是正数,求证:
(2)(x+y)(x2+y2)(x3+y3)≥ 8x3y3。
随堂练习
1、已知a、b、c都是正数,
求证:(a+b)(b+c)(c+a)≥ 8abc。
变式、已知a、b、c都是正数,a + b + c = 1,
求证:(1 – a)(1 – b)(1 – c)≥ 8abc。
2、证明:a2+b2+c2≥ ab + bc + ca。
变式:已知a、b、c都是正数,证明:
1.凑项
:使积成为定值
4
5
1
32
2.凑系数
:使和成为定值
3.分离法
9
2
1
4.关于“1”的灵活运用
变式:
16
16
例:已知lgx+lgy=1, 的最小值是______.
2
5.基本不等式与对数相结合
2
几种利用基本不等式求最值的技巧:
2.凑系数
1.凑项
3.分离
4.“1”的妙用
小结:
作业:
