高中数学人教版必修5课件:3.2一元二次不等式及其解法(共30张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:3.2一元二次不等式及其解法(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 15:16:06 | ||
图片预览









文档简介
(共30张PPT)
§3.2 一元二次不等式及其解法(一)
高一数学
学习目标:
1、掌握一元二次不等式的解法;
2、利用一元二次函数与一元二次方程来求解
一元二次不等式,理解三者之间的关系。
(1)公式法 x=
(2)配方法:
(3)十字相乘法
ax2+bx+c=0(a≠0)
1.一元二次方程的一般形式是什么呢?
y=ax2+bx+c(a≠0)
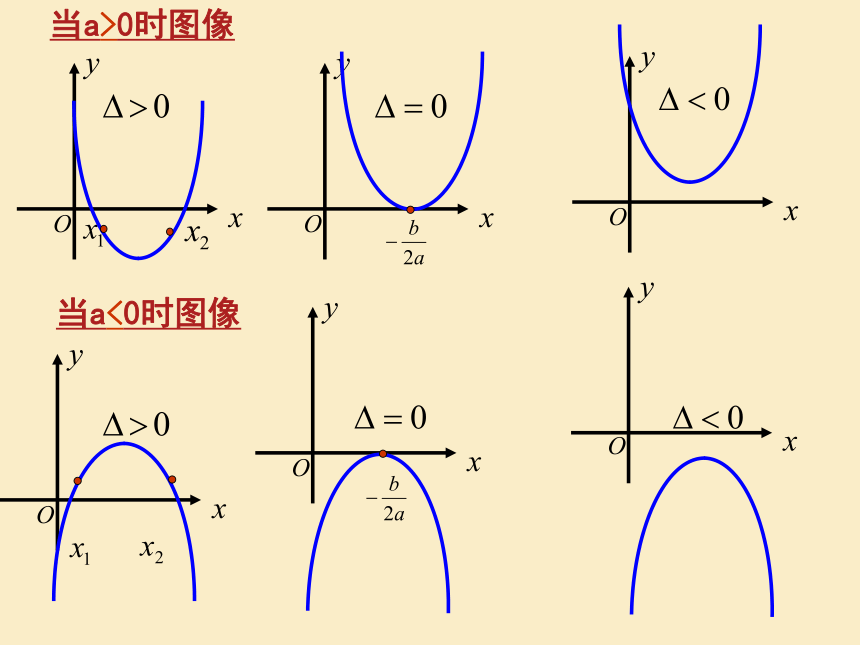
当a>0时图像
当a<0时图像
学校要在长为8,宽为6 的一块长方形地面上进行绿化,计划四周种花卉,花卉带的宽度相同,中间种植草坪(图中阴影部分)为了美观,现要求草坪的种植面积超过总面积的一半,此时花卉带的宽度的取值范围是什么?
整理得
整理得
创设情景 引入新课
一元二次不等式的一般形式:
一元二次不等式的定义:
只含有一个未知数,并且未知数最高次数是 2 的不等式叫做一元二次不等式.
ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)
其中a,b,c均为常数。
一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
即 f(x)=ax2+bx+c (a≠0),
ax2+bx+c≥0 (a≠0) 或ax2+bx+c≤0 (a≠0)
它们之间有怎样的联系呢?
一元二次方程:
ax2+bx+c=0(a≠0)
一元二次不等式:
ax2+bx+c>0(a≠0)
或ax2+bx+c<0(a≠0)
二次函数:
y=ax2+bx+c(a≠0)
一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。
一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。
因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。
方程的解即函数图象与x轴交点的横坐标,
不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。
利用二次函数图象能解一元二次不等式!
练习 下面哪些是一元二次不等式
(其中a、b、c、m为常数)?
解:(1)(2)是;(3)(4)(5)不是.
(3)不是,∵a=0时,不符合定义;
(4)不是,x的最高次数是3,不符合定义;
(5)不是,m=0时,是一元一次不等式;m≠0时,
是二元二次不等式.
紧扣定义
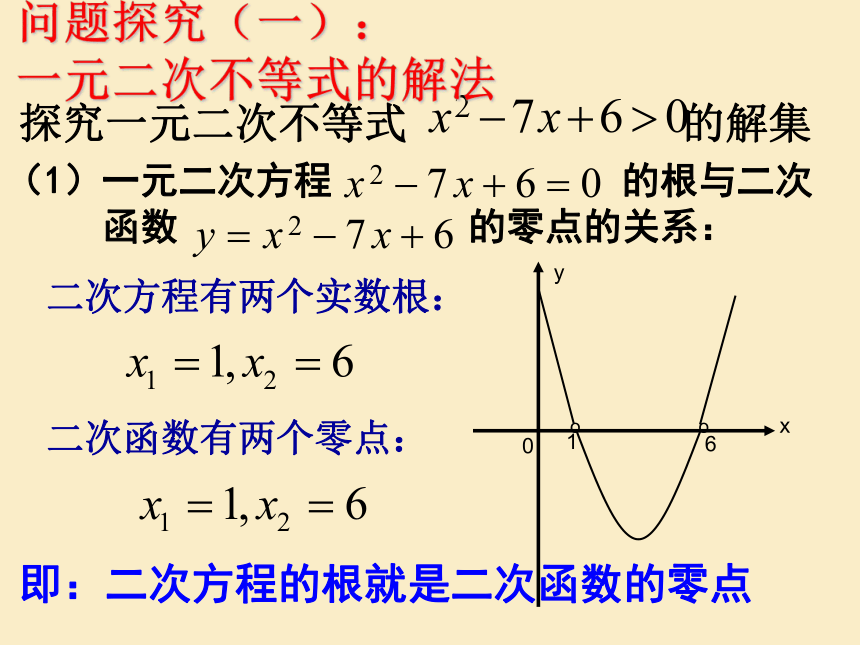
二次方程有两个实数根:
二次函数有两个零点:
即:二次方程的根就是二次函数的零点
问题探究(一):
一元二次不等式的解法
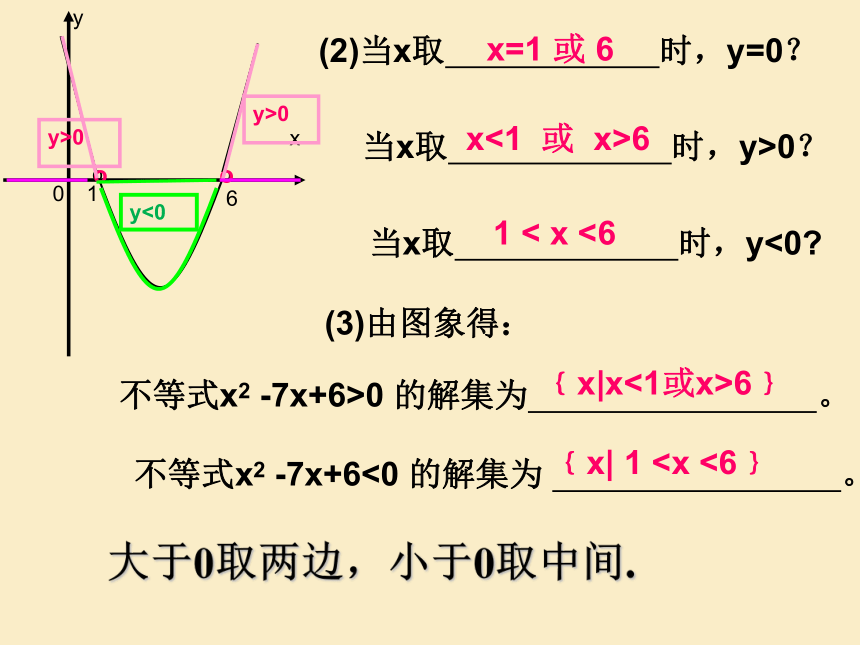
不等式x2 -7x+6>0 的解集为 。
不等式x2 -7x+6<0 的解集为 。
x<1 或 x>6
y
x
0
(2)当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
x=1 或 6
1 < x <6
﹛x|x<1或x>6﹜
﹛x| 1大于0取两边,小于0取中间.
(3)由图象得:
△>0
有两相异实根
x1, x2 (x1{x|xx2}
{x|x1< x△=0
△<0
有两相等实根
x1=x2=
{x|x≠ }
Φ
Φ
R
没有实根
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
判别式
△=b2- 4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(y>0)的解集
ax2+bx+c<0
(y<0)的解集
求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:
x< x1或x> x2
思考
若a<0时,先变形!
a>0
典例剖析 规范步骤
典例剖析 规范步骤
通过以上两例,我们不难对一元二次不等式ax2+bx+c>0 (a>0)和ax2+bx+c<0 (a>0)解集的形式作一般性的分析。
设方程ax2+bx+c=0 (a>0)的判别式为△。
(1)当△>0时,二次方程ax2+bx+c=0有两个不等的实数根x1,x2,(设x1 考察这类二次函数f(x)=ax2+bx+c的图象,这时,函数的零点把x轴分成三个区间
(-∞,x1),(x1,x2),(x2,+∞),
不等式ax2+bx+c>0的解集是(-∞,x1)∪ (x2,+∞),不等式ax2+bx+c<0的解集是(x1,x2).
简单的说是:
大于在两边,小于在中间。
(2)当△=0时,通过配方得,
由图可知,ax2+bx+c>0的解集是 的全体实数,即
ax2+bx+c<0的解集是空集,即不等式无解。
3)当△<0时,二次函数f(x)=ax2+bx+c的图象在x轴上方,由此可知,
不等式ax2+bx+c>0的解集是实数集R,不等式ax2+bx+c<0的解集是空集。
一看:看二次项系数是否为正,若为 负化为正。
求一元二次不等式的的一般步骤:
二算:算△及对应方程的根。
三写:由对应方程的根,结合不等号的方向,根据函数图象写出不等式的解集。(大于取两边,小于取中间)
练习:解下列不等式:
当堂训练 巩固深化
典例剖析 规范步骤
解下列不等式:
当堂训练 巩固深化
典例剖析 规范步骤
当堂训练 巩固深化
课堂小结
1.求解一元二次不等式的三个步骤:
(1).将不等式化为标准形式:
ax2+bx+c>0 或 ax2+bx+c<0
(2).解出相应的方程的根。
(3).画出相应二次函数的草图,根据草图确定所求不等式的解集。
再次强调注意公式口诀的大前提: a>0
1.一元二次不等式的定义与一般形式.
2.三个“二次”的关系.
3.一元二次不等式的解法及其步骤.
4.数学思想:数形结合的思想.
5.认识方法:特殊到一般的辩证法.
小结
§3.2 一元二次不等式及其解法(一)
高一数学
学习目标:
1、掌握一元二次不等式的解法;
2、利用一元二次函数与一元二次方程来求解
一元二次不等式,理解三者之间的关系。
(1)公式法 x=
(2)配方法:
(3)十字相乘法
ax2+bx+c=0(a≠0)
1.一元二次方程的一般形式是什么呢?
y=ax2+bx+c(a≠0)
当a>0时图像
当a<0时图像
学校要在长为8,宽为6 的一块长方形地面上进行绿化,计划四周种花卉,花卉带的宽度相同,中间种植草坪(图中阴影部分)为了美观,现要求草坪的种植面积超过总面积的一半,此时花卉带的宽度的取值范围是什么?
整理得
整理得
创设情景 引入新课
一元二次不等式的一般形式:
一元二次不等式的定义:
只含有一个未知数,并且未知数最高次数是 2 的不等式叫做一元二次不等式.
ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)
其中a,b,c均为常数。
一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
即 f(x)=ax2+bx+c (a≠0),
ax2+bx+c≥0 (a≠0) 或ax2+bx+c≤0 (a≠0)
它们之间有怎样的联系呢?
一元二次方程:
ax2+bx+c=0(a≠0)
一元二次不等式:
ax2+bx+c>0(a≠0)
或ax2+bx+c<0(a≠0)
二次函数:
y=ax2+bx+c(a≠0)
一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。
一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。
因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。
方程的解即函数图象与x轴交点的横坐标,
不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。
利用二次函数图象能解一元二次不等式!
练习 下面哪些是一元二次不等式
(其中a、b、c、m为常数)?
解:(1)(2)是;(3)(4)(5)不是.
(3)不是,∵a=0时,不符合定义;
(4)不是,x的最高次数是3,不符合定义;
(5)不是,m=0时,是一元一次不等式;m≠0时,
是二元二次不等式.
紧扣定义
二次方程有两个实数根:
二次函数有两个零点:
即:二次方程的根就是二次函数的零点
问题探究(一):
一元二次不等式的解法
不等式x2 -7x+6>0 的解集为 。
不等式x2 -7x+6<0 的解集为 。
x<1 或 x>6
y
x
0
(2)当x取 时,y=0?
当x取 时,y>0?
当x取 时,y<0?
x=1 或 6
1 < x <6
﹛x|x<1或x>6﹜
﹛x| 1
(3)由图象得:
△>0
有两相异实根
x1, x2 (x1
{x|x1< x
△<0
有两相等实根
x1=x2=
{x|x≠ }
Φ
Φ
R
没有实根
函数 、方程、不等式之间的关系
y>0
y>0
y>0
y<0
判别式
△=b2- 4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(y>0)的解集
ax2+bx+c<0
(y<0)的解集
求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:
x< x1或x> x2
思考
若a<0时,先变形!
a>0
典例剖析 规范步骤
典例剖析 规范步骤
通过以上两例,我们不难对一元二次不等式ax2+bx+c>0 (a>0)和ax2+bx+c<0 (a>0)解集的形式作一般性的分析。
设方程ax2+bx+c=0 (a>0)的判别式为△。
(1)当△>0时,二次方程ax2+bx+c=0有两个不等的实数根x1,x2,(设x1
(-∞,x1),(x1,x2),(x2,+∞),
不等式ax2+bx+c>0的解集是(-∞,x1)∪ (x2,+∞),不等式ax2+bx+c<0的解集是(x1,x2).
简单的说是:
大于在两边,小于在中间。
(2)当△=0时,通过配方得,
由图可知,ax2+bx+c>0的解集是 的全体实数,即
ax2+bx+c<0的解集是空集,即不等式无解。
3)当△<0时,二次函数f(x)=ax2+bx+c的图象在x轴上方,由此可知,
不等式ax2+bx+c>0的解集是实数集R,不等式ax2+bx+c<0的解集是空集。
一看:看二次项系数是否为正,若为 负化为正。
求一元二次不等式的的一般步骤:
二算:算△及对应方程的根。
三写:由对应方程的根,结合不等号的方向,根据函数图象写出不等式的解集。(大于取两边,小于取中间)
练习:解下列不等式:
当堂训练 巩固深化
典例剖析 规范步骤
解下列不等式:
当堂训练 巩固深化
典例剖析 规范步骤
当堂训练 巩固深化
课堂小结
1.求解一元二次不等式的三个步骤:
(1).将不等式化为标准形式:
ax2+bx+c>0 或 ax2+bx+c<0
(2).解出相应的方程的根。
(3).画出相应二次函数的草图,根据草图确定所求不等式的解集。
再次强调注意公式口诀的大前提: a>0
1.一元二次不等式的定义与一般形式.
2.三个“二次”的关系.
3.一元二次不等式的解法及其步骤.
4.数学思想:数形结合的思想.
5.认识方法:特殊到一般的辩证法.
小结
