重庆市巴蜀中学人教版高中物理必修一学案:第3章 第3练 共点力的平衡问题
文档属性
| 名称 | 重庆市巴蜀中学人教版高中物理必修一学案:第3章 第3练 共点力的平衡问题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-30 13:50:54 | ||
图片预览


文档简介
第3练 力的合成与力的分解
基础知识梳理
1.共点力作用下物体的平衡
(1)平衡状态
物体处于静止或匀速直线运动的状态.
(2)共点力的平衡条件:F合=0或者
2.共点力平衡的几条重要推论
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,这两个力必定大小相等,方向相反.
(2)三力平衡:如果物体在三个共点力的作用下处于平衡状态,其中任意两个力的合力一定与第三个力大小相等,方向相反.
(3)多力平衡:如果物体受多个力作用处于平衡状态,其中任何一个力与其余力的合力大小相等,方向相反.
3.求解共点力作用下物体平衡问题的解题步骤:
1.确定研究对象;
2.对研究对象进行受力分析,并画受力图;
3.据物体的受力和已知条件,采用力的合成、分解、图解、正交分解法,确定解题方法;
4.解方程,进行讨论和计算。
4.可能涉及到的解题方法;
1.几何法(矢量三角形或平行四边形;正弦定理;三角函数;相似三角形法等);
2.整体法、隔离法;
3.函数法;
4.极值法。
考向分析
考向一受力分析 整体法与隔离法的应用
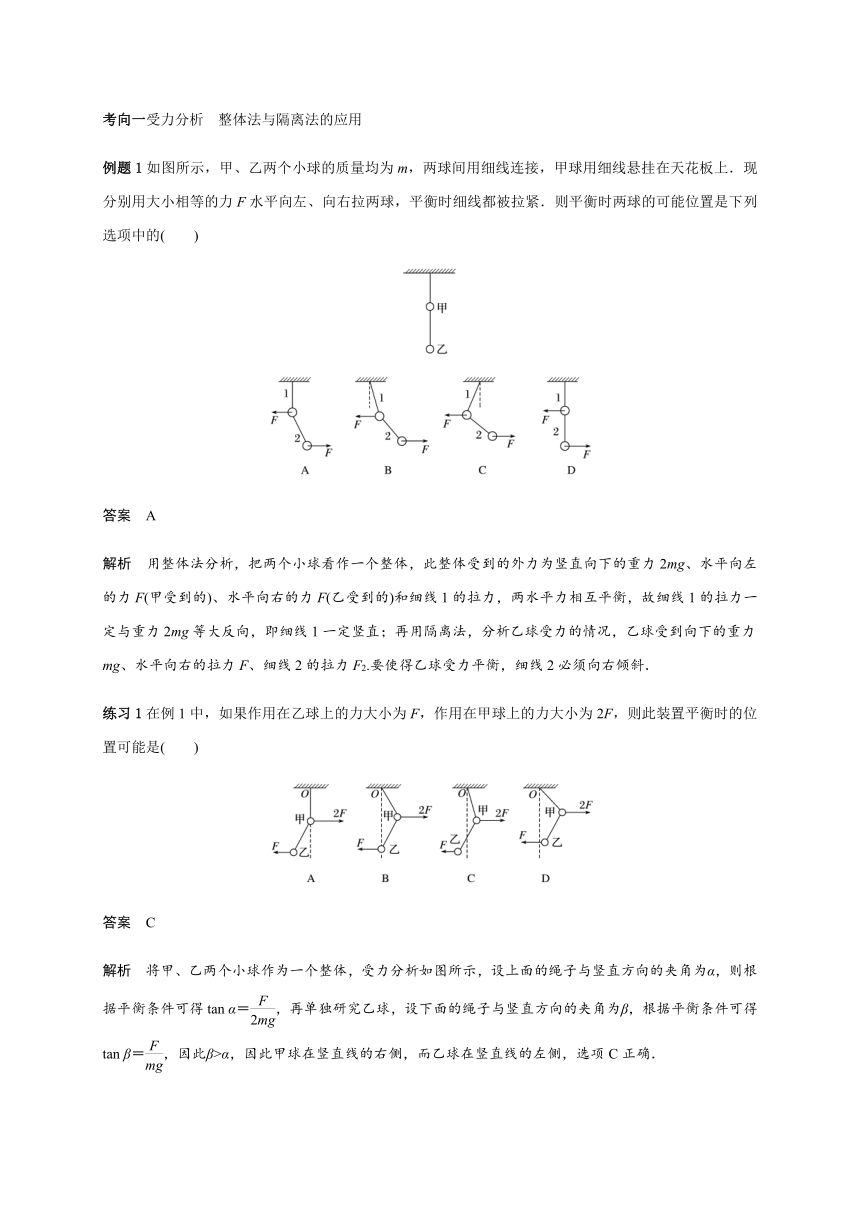
例题1如图所示,甲、乙两个小球的质量均为m,两球间用细线连接,甲球用细线悬挂在天花板上.现分别用大小相等的力F水平向左、向右拉两球,平衡时细线都被拉紧.则平衡时两球的可能位置是下列选项中的( )
答案 A
解析 用整体法分析,把两个小球看作一个整体,此整体受到的外力为竖直向下的重力2mg、水平向左的力F(甲受到的)、水平向右的力F(乙受到的)和细线1的拉力,两水平力相互平衡,故细线1的拉力一定与重力2mg等大反向,即细线1一定竖直;再用隔离法,分析乙球受力的情况,乙球受到向下的重力mg、水平向右的拉力F、细线2的拉力F2.要使得乙球受力平衡,细线2必须向右倾斜.
练习1在例1中,如果作用在乙球上的力大小为F,作用在甲球上的力大小为2F,则此装置平衡时的位置可能是( )
答案 C
解析 将甲、乙两个小球作为一个整体,受力分析如图所示,设上面的绳子与竖直方向的夹角为α,则根据平衡条件可得tan α=,再单独研究乙球,设下面的绳子与竖直方向的夹角为β,根据平衡条件可得tan β=,因此β>α,因此甲球在竖直线的右侧,而乙球在竖直线的左侧,选项C正确.
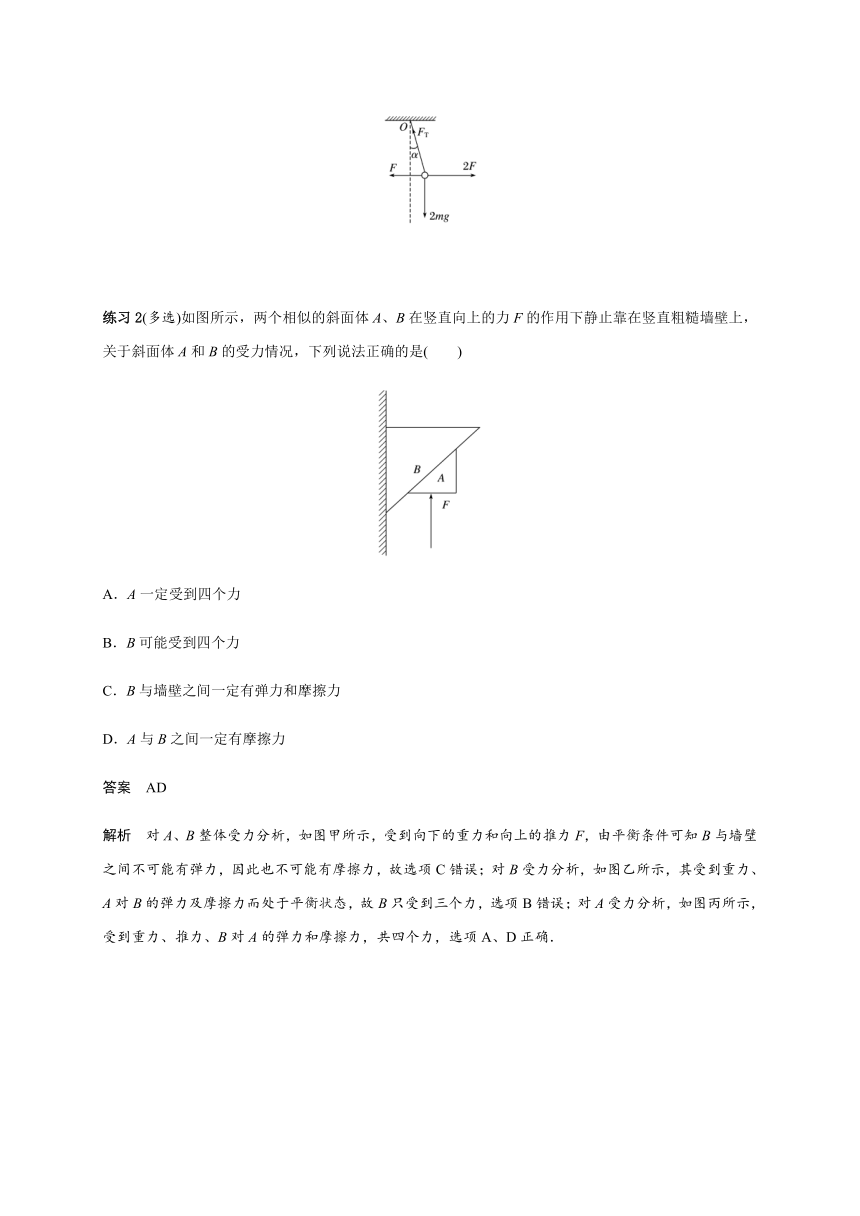
练习2(多选)如图所示,两个相似的斜面体A、B在竖直向上的力F的作用下静止靠在竖直粗糙墙壁上,关于斜面体A和B的受力情况,下列说法正确的是( )
A.A一定受到四个力
B.B可能受到四个力
C.B与墙壁之间一定有弹力和摩擦力
D.A与B之间一定有摩擦力
答案 AD
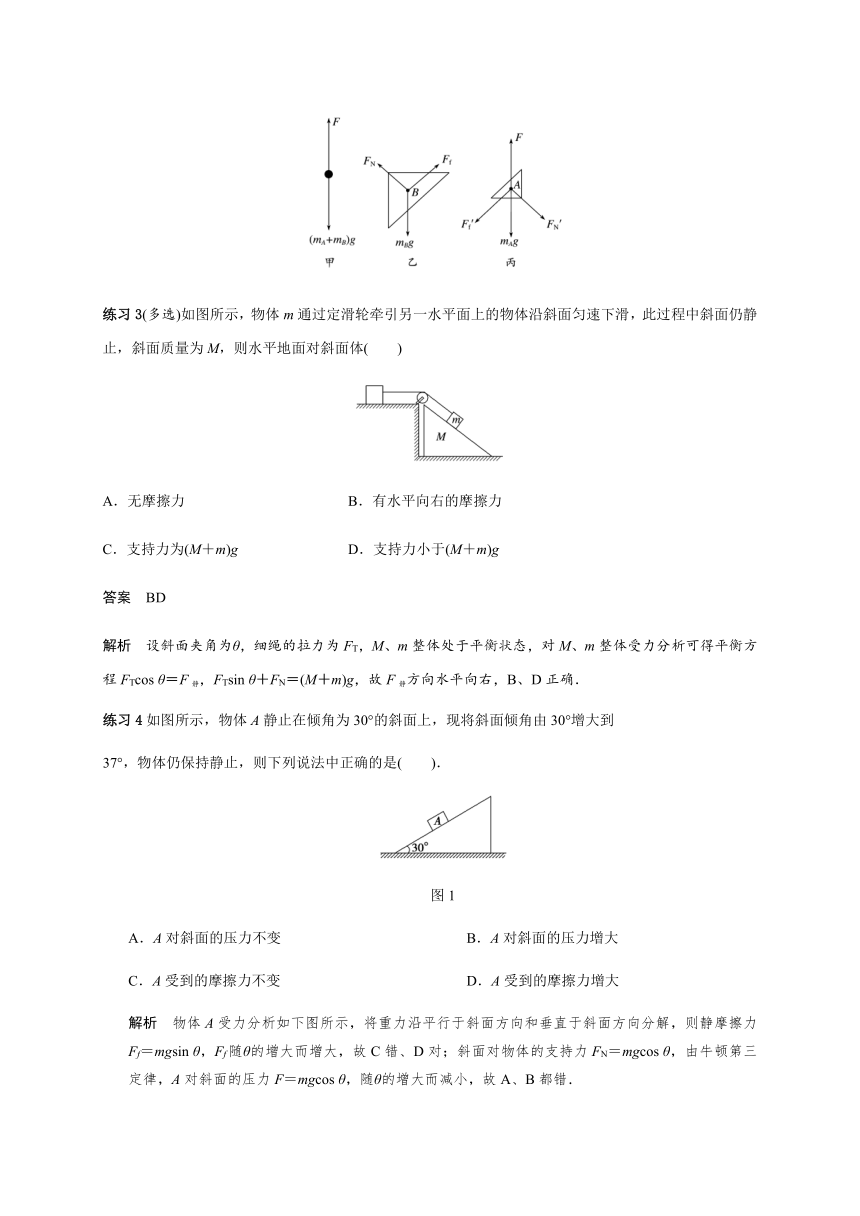
解析 对A、B整体受力分析,如图甲所示,受到向下的重力和向上的推力F,由平衡条件可知B与墙壁之间不可能有弹力,因此也不可能有摩擦力,故选项C错误;对B受力分析,如图乙所示,其受到重力、A对B的弹力及摩擦力而处于平衡状态,故B只受到三个力,选项B错误;对A受力分析,如图丙所示,受到重力、推力、B对A的弹力和摩擦力,共四个力,选项A、D正确.
练习3(多选)如图所示,物体m通过定滑轮牵引另一水平面上的物体沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平地面对斜面体( )
A.无摩擦力 B.有水平向右的摩擦力
C.支持力为(M+m)g D.支持力小于(M+m)g
答案 BD
解析 设斜面夹角为θ,细绳的拉力为FT,M、m整体处于平衡状态,对M、m整体受力分析可得平衡方程FTcos θ=F静,FTsin θ+FN=(M+m)g,故F静方向水平向右,B、D正确.
练习4如图所示,物体A静止在倾角为30°的斜面上,现将斜面倾角由30°增大到
37°,物体仍保持静止,则下列说法中正确的是( ).
图1
A.A对斜面的压力不变 B.A对斜面的压力增大
C.A受到的摩擦力不变 D.A受到的摩擦力增大
解析 物体A受力分析如下图所示,将重力沿平行于斜面方向和垂直于斜面方向分解,则静摩擦力Ff=mgsin θ,Ff随θ的增大而增大,故C错、D对;斜面对物体的支持力FN=mgcos θ,由牛顿第三定律,A对斜面的压力F=mgcos θ,随θ的增大而减小,故A、B都错.
答案 D
练习5一质量为m的物块恰好静止在倾角为θ的斜面上.现对物块施加一个竖直向下的恒力F,如图所示.则物块( )
A.仍处于静止状态
B.沿斜面加速下滑
C.受到的摩擦力不变
D.受到的合外力增大
解析 物块恰好静止在斜面上,沿斜面方向有:mgsin θ=μmgcos θ,得μ=tan θ,摩擦力f=mgsin θ.施加一个竖直向下的恒力F后,沿斜面向下的力(mg+F)sin θ与沿斜面向上的力μ(mg+F)cos θ仍然相等,所以物块仍处于静止状态,合外力不变,仍为零,故A正确,B、D错误.受到的摩擦力f′=(mg+F)sin θ,变大,故C错误.
答案 A
练习6如图所示,在倾斜的滑杆上套一个质量为m的圆环,圆环通过轻绳拉着一个质量为M的物体,在圆环沿滑杆向下滑动的过程中,悬挂物体的轻绳始终处于竖直方向.则( ).
A.环只受三个力作用
B.环一定受四个力作用
C.物体做匀加速运动
D.悬绳对物体的拉力小于物体的重力
解析 分析M可知,其受两个力作用,重力和轻绳拉力,因为悬挂物体的轻绳始终处于竖直方向,故二力平衡,物体做匀速运动,C、D错误;再对环进行受力分析可知,环受重力、轻绳拉力、滑杆支持力和摩擦力,A错、B正确.
答案 B
练习7如图所示,A、B两物体叠放在水平地面上,A物体质量m=20 kg,B物体质量M=30 kg.处于水平位置的轻弹簧一端固定于墙壁,另一端与A物体相连,弹簧处于自然状态,其劲度系数为250 N/m,A与B之间、B与地面之间的动摩擦因数均为μ=0.5.现有一水平推力F作用于物体B上缓慢地向墙壁移动,当移动0.2 m时,水平推力F的大小为(g取10 m/s2)( )
A.350 N B.300 N
C.250 N D.200 N
解析 由题意可知fAmax=μmg=100 N.当A向左移动0.2 m时,F弹=kΔx=50 N,F弹
练习8如图所示,木块m和M叠放在一固定在地面不动的斜面上,它们一起沿斜面匀速下滑,则m、M间的动摩擦因数μ1和M、斜面间的动摩擦因数μ2可能正确的有( ).
A.μ1=0,μ2=0 B.μ1=0,μ2≠0
C.μ1≠0,μ2=0 D.μ1≠0,μ2≠0
解析 因木块m和M整体沿斜面匀速下滑,所以M与斜面之间一定存在摩擦力,故M、斜面间的动摩擦因数μ2一定不等于零;因木块m和M的接触面水平,由m的运动状态可知,它一定不受M的摩擦力,所以木块m和M之间的动摩擦因数μ1可以为零,也可以不为零,B、D项正确.
答案 BD
练习9如图所示,质量为m、横截面为直角三角形的物块ABC,∠BAC=α,AB边靠在竖直墙面上,F是垂直于斜面AC的推力.物块与墙面间的动摩擦因数为μ(μ<1).现物块静止不动,则( ).
A.物块可能受到4个力作用
B.物块受到墙的摩擦力的方向一定向上
C.物块对墙的压力一定为Fcos α
D.物块受到摩擦力的大小可能等于F
解析 本题的静摩擦力有临界点.假设Fsin α=mg,则没有摩擦力,物块受mg、F、墙的支持力FN三个力作用.假设Fsin α
答案 AC
练习10如图所示,直角三角形框架ABC(角C为直角)固定在水平地面上,已知AC与水平方向的夹角为α=30°.小环P、Q分别套在光滑臂AC、BC上,用一根细绳连接两小环,静止时细绳恰好处于水平方向,小环P、Q的质量分别为m1、m2,则小环P、Q的质量之比为
( ).
A.= B.=3
C.= D.=
解析 分析P的受力情况如下图所示,根据平衡条件,可得T=m1gtan 30°.对Q同理可得T=m2gtan 60°,由此得=3,选项B正确.
练习11如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止,现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法正确的是( )
A.A、B之间的摩擦力一定变大 B.B与墙面间的弹力可能不变
C.B与墙之间可能没有摩擦力 D.弹簧弹力一定不变
答案 D
解析 对A分析,开始受重力、B对A的支持力和静摩擦力平衡,当施加F后,仍然处于静止状态,开始A所受的静摩擦力大小为mAgsin θ,若F=2mAgsin θ,则A、B之间的摩擦力大小不变,故A错误;以A、B整体为研究对象,开始时B与墙面的弹力为零,后来施加F后,弹力为Fcos θ,B错误;对A、B整体分析,由于A、B不动,弹簧的形变量不变,则弹簧的弹力不变,开始弹簧的弹力等于A、B的总重力,施加F后,弹簧的弹力不变,总重力不变,根据平衡知,则B与墙之间一定有摩擦力,故C错误,D正确.
练习12(2017·浙江省模拟)如图所示,纯净水桶和简易金属支架静止于水平桌面上,则( )
A.桌面对支架的摩擦力水平向左
B.水桶对支架的作用力竖直向下
C.支架对水桶的作用力斜向右上方
D.支架对桌面的压力大小等于支架的重力
答案 B
解析 A、D两项,对水桶和支架整体,受重力和支持力,二力平衡,故桌面对支架没有摩擦力,否则不平衡;支架对桌面的压力等于整体的重力,大于支架的重力,故A项错误,D项错误;B、C两项,隔离水桶分析,受重力和支架的支持力,根据平衡条件,支持力与重力等值、反向、共线,故支架对水桶的作用力竖直向上,根据牛顿第三定律,水桶对支架的作用力竖直向下,故B项正确,C项错误;故选B项.
练习13(2017·湛江模拟)(多选)如图所示,物体B靠在水平天花板上,在竖直向上的力F作用下,A、B保持静止,A与B间的动摩擦因数为μ1,B与天花板间的动摩擦因数为μ2,则关于μ1、μ2的值下列判断可能正确的是
( )
A.μ1=0,μ2≠0 B.μ1≠0,μ2=0
C.μ1=0,μ2=0 D.μ1≠0,μ2≠0
答案 BD
解析 选A、B组成的整体为研究对象,水平方向不受力作用,故水平方向的滑动摩擦力为零,故μ2可以为零,也可以不为零,再以B为研究对象,可分析出A、B之间有摩擦力作用,故μ1一定不为零,故B、D项正确.
练习14(2017·盐湖区一模)在竖直墙壁间有质量分别是m和2m的半圆球A和圆球B,其中B球球面光滑,半球A与左侧墙壁之间存在摩擦.两球心之间连线与水平方向成30°的夹角,两球恰好不下滑,设最大静摩擦力等于滑动摩擦力,(g为重力加速度),则半球A与左侧墙壁之间的动摩擦因数为( )
A. B.
C. D.
答案 A
解析 隔离光滑均匀圆球B,对B受力分析如图所示,可得:
FN=Fcosθ
2mg-Fsinθ=0
解得:FN=,
对两球组成的整体有:
3mg-μFN=0
联立解得:μ=
练习15两个相同的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两小球,然后,用一水平方向的力F作用在小球A上,此时三根细线均处于直线状态,且OB细线恰好处于竖直方向,如图所示.如果不考虑小球的大小,两小球均处于静止状态,则:
(1)OB绳对小球的拉力为多大?
(2)OA绳对小球的拉力为多大?
(3)作用力F为多大?
解析 (1)因OB绳处于竖直方向,所以B球处于平衡状态,AB绳上的拉力为零,OB绳对小球的拉力FOB=mg.
(2)A球在重力mg、水平拉力F和OA绳的拉力FOA三力作用下平衡,所以OA绳对小球的拉力FOA==2mg.
(3)作用力F=mgtan 60°=mg.
答案 (1)mg (2)2mg (3)mg
练习16(多选)如图所示,粗糙水平面上有一长木板,一个人站在木板上用力F向右推箱子,木板、人、箱子均处于静止状态.三者的质量均为m,下列说法正确的是( )
A.箱子受到的摩擦力方向向右
B.人受到的摩擦力方向向右
C.箱子对木板的摩擦力方向向右
D.若水平面光滑,人用同样大小的力F推箱子,能使长木板在水平面上滑动
答案 BC
练习17(多选)如图所示,木板C放在水平地面上,木板B放在C的上面,木板A放在B的上面,A的右端通过轻质弹簧测力计固定在竖直的墙壁上,A、B、C质量相等,且各接触面动摩擦因数相同,用大小为F的水平力向左拉动C,使它以速度v匀速运动,三者稳定后弹簧测力计的示数为Ff.设最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )
A.B对A的摩擦力大小为Ff,方向向左
B.A和B保持静止,C匀速运动
C.A保持静止,B和C一起匀速运动
D.C受到地面的摩擦力大小为F-Ff
答案 ACD
考向二矢量三角形法(一个力大小方向都不变,一个力方向不变)
例题1(多选)如图所示,质量分布均匀的光滑小球O,放在倾角均为θ的斜面体上,斜面体位于同一水平面上,且小球处于平衡,则下列说法中正确的是( )
A.甲图中斜面对球O弹力最大
B.丙图中斜面对球O弹力最小
C.乙图中挡板MN对球O弹力最小
D.丙图中挡板MN对球O弹力最小
答案 AD
解析 将甲、乙、丙、丁四种情况小球的受力图作于一幅图上,如图,根据平衡条件得知,丁图中斜面对小球的弹力为零,挡板对小球的弹力等于其重力G.斜面对小球的弹力和挡板对小球的弹力的合力与重力大小相等、方向相反,可知三种情况下此合力相等,根据平行四边定则得知,丙图中挡板MN对球O弹力最小,甲图中斜面对球O弹力最大.故B、C错误,A、D正确.
练习1质量为m的物体用轻绳AB悬挂于天花板上.用水平向左的力F缓慢拉动绳的中点O,如图所示.用T表示绳OA段拉力的大小,在O点向左移动的过程中( )
A.F逐渐变大,T逐渐变大
B.F逐渐变大,T逐渐变小
C.F逐渐变小,T逐渐变大
D.F逐渐变小,T逐渐变小
答案 A
解析 对O点受力分析如图所示,F与T的变化情况如图,由图可知在O点向左移动的过程中,F逐渐变大,T逐渐变大,故选项A正确.
练习2将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线OA与竖直方向的夹角保持θ=30°,则F的最小值为( )
A.mg B.mg C.mg D.mg
答案 B
解析 以a、b为整体,整体受重力2mg、悬绳OA的拉力FT及拉力F三个力而平衡,如图所示,三力构成的矢量三角形中,当力F垂直于悬绳的拉力FT时有最小值,且最小值F=2mgsin θ=mg,B项正确.
练习3如图所示,质量为m的物体放在一固定斜面上,当斜面倾角为30°时恰能沿斜面匀速下滑.对物体施加一大小为F水平向右的恒力,物体可沿斜面匀速向上滑行.设最大静摩擦力等于滑动摩擦力,当斜面倾角增大并超过某一临界角θ0时,不论水平恒力F多大,都不能使物体沿斜面向上滑行,试求:
(1)物体与斜面间的动摩擦因数;
(2)这一临界角θ0的大小.
答案 (1) (2)60°
解析 (1)如图所示,未施加力F时,对物体受力分析,由平衡条件得mgsin 30°=μmgcos 30°
解得μ=tan 30°=
(2)设斜面倾角为α时,受力情况如图所示,由平衡条件得:
Fcos α=mgsin α+Ff′
FN′=mgcos α+Fsin α
Ff′=μFN′
解得F=
当cos α-μsin α=0,即tan α=时,F→∞,即“不论水平恒力F多大,都不能使物体沿斜面向上滑行”,此时,临界角θ0=α=60°.
练习4.(多选)如图,用OA、OB两根轻绳将花盆悬于两竖直墙之间,开始时OB绳水平.现保持O点位置不变,改变OB绳长使绳右端由B点缓慢上移至B′点,此时OB′与OA之间的夹角θ<90°.设此过程OA、OB绳的拉力分别为FOA、FOB,则下列说法正确的是( )
A.FOA一直减小
B.FOA一直增大
C.FOB一直减小
D.FOB先减小后增大
答案 AD
解析 以结点O为研究对象,分析受力:重力G、绳OA的拉力FOA和绳OB的拉力FOB,如图所示,根据平衡条件知,两根绳子的拉力的合力与重力大小相等、方向相反,作出轻绳OB在两个位置时力的合成图如图,由图看出,FOA逐渐减小,FOB先减小后增大,当θ=90°时,FOB最小.
练习5如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.若把A向右移动少许后,它们仍处于静止状态.则下列判断中正确的是( )
A.球B对墙的压力增大
B.球B对柱状物体A的压力增大
C.地面对柱状物体A的摩擦力不变
D.地面对柱状物体A的支持力不变
答案 D
解析 球B受重力、A的支持力F1和墙壁的压力F2.如图甲所示:
将重力G分解为G1和G2,则根据平衡可知,F1=G1=,F2=G2=Gtan θ.当A向右移动少许,根据题意可知,A对球B的作用力F1与竖直方向的夹角θ将减小,所以cos θ增大,tan θ减小,即墙壁对球B的作用力将减小,A对小球B的支持力减小.根据牛顿第三定律可知,球B对墙壁的压力将减小,球B对A的压力亦减小.选项A、B错误;再对A进行受力分析如图乙:由于A处于平衡状态,所以A受地面摩擦力Ff=FBsin θ,根据题意知,B对A的压力FB减小且FB与竖直方向的夹角θ减小,故A所受地面的摩擦力Ff减小.选项C错误;对整体受力分析可知,地面对A的支持力等于A、B的重力之和,故选项D正确;故选D.
练习6如图所示,桌面上固定一个光滑的竖直挡板,现将一个质量一定的重球A与截面为三角形的垫块B叠放在一起,用水平外力F可以缓缓向左推动B,使球慢慢升高,设各接触面均光滑,则该过程中( )
A.A和B均受三个力作用而平衡
B.B对桌面的压力越来越大
C.A对B的压力越来越小
D.推力F的大小恒定不变
解析 分析A、B整体受力如图甲所示,由平衡条件可得:
NB=(mA+mB)g,不随球的升高而改变,故B错误;
分析球A受力如图乙所示,由平衡条件可得:NAB=mg/cos θ,NA=mgtan θ,并不随球的升高而改变,故缓慢推动B的过程中F也不变,C错误、D正确;垫块B受支持力、压力、重力、推力F四个力作用,A错误.
答案 D
练习7(2017·广东汕头二模)重力都为G的两个小球A和B用三段轻绳如图所示连接后悬挂在O点上,O、B间的绳子长度是A、B间的绳子长度的2倍,将一个拉力F作用到小球B上,使三段轻绳都伸直且O、A间和A、B间的两段绳子分别处于竖直和水平方向上,则拉力F的最小值为( )
A.G B.G C.G D.G
答案 A
解析 对A球受力分析可知,因O、A间绳竖直,则A、B间绳上的拉力为0.对B球受力分析如图所示,则可知当F与O、B间绳垂直时F最小,Fmin=Gsin θ,其中sin θ==,则Fmin=G,故A项正确.
练习8(2018·山西太原调研)如图所示,轻绳OA一端固定在天花板上,另一端系一光滑的圆环,一根系着物体的轻绳穿过圆环后,另一端固定在墙上B点,且OB处于水平.现将A点缓慢沿天花板水平向右移动,且OB段的轻绳始终保持水平,则OA、OB段轻绳所受的拉力的大小FTA、FTB的变化情况是( )
A.FTA增大,FTB不变 B.FTA、FTB均不变 C.FTA不变,FTB增大 D.FTA、FTB均减小
答案 B
解析 因为圆环光滑,则OC、OB段轻绳所受的拉力的大小FTC、FTB始终相等,且等于物体的重力.又OB段轻绳始终保持水平,OC段轻绳始终保持竖直,则A点缓慢右移,圆环也随之右移,角θ不变,由平衡条件可知OA段绳上所受的拉力不变.故B项正确.
练习9(2018·河北唐山质检)光滑斜面上固定着一根刚性圆弧形细杆,小球通过轻绳与细杆相连,此时轻绳处于水平方向,球心恰位于圆弧形细杆的圆心处,如图所示.将悬点A缓慢沿杆向上移动,直到轻绳处于竖直方向,在这个过程中,轻绳的拉力( )
A.逐渐增大 B.大小不变 C.先减小后增大 D.先增大后减小
答案 C
解析 当悬点A缓慢向上移动过程中,小球始终处于平衡状态,小球所受重力mg的大小和方向都不变,支持力的方向不变,对球进行受力分析如图所示,由图可知,拉力FT先减小后增大,C项正确.
练习10如图所示,质量为m的小球用细线拴住放在光滑斜面上,斜面足够长,倾角为α的斜面体置于光滑水平面上,用水平力F推斜面体使斜面体缓慢地向左移动,小球沿斜面缓慢升高(细绳尚未到达平行于斜面的位置).在此过程中:( )
A.绳对小球的拉力减小 B.斜面体对小球的支持力减小
C.水平推力F减小 D.地面对斜面体的支持力不变
答案 A
解析 对小球受力分析,如图甲所示,斜面体左移会引起FT的方向及大小的变化而FN的方向不变,三力的合力为0,则形成闭合三角形,FT与FN相互垂直时FT最小,此时细线和斜面平行,则细线尚未到达平行于斜面的位置时,FT逐渐变小,FN逐渐变大,故选项A正确,B错误;对斜面体受力分析,如图乙所示,根据平衡条件,有:F=FN′sin α=FNsin α,FN地=Mg+FN′cos α=Mg+FNcos α.由于FN增大,故支持力FN地和推力F均增大,故C、D错误.
练习11(多选)如图所示,斜面体置于粗糙水平面上,斜面光滑.小球被轻质细线系住放在斜面上.细线另一端跨过定滑轮,用力拉细线使小球沿斜面缓慢下移一小段距离,斜面体始终静止.移动过程中( )
A.细线对小球的拉力变大 B.斜面对小球的支持力变大
C.斜面对地面的压力变大 D.地面对斜面的摩擦力变大
答案 BCD
解析 设小球和斜面体的质量分别为m和M,细线和斜面的夹角为θ.
对小球受力分析,如图甲所示,小球受到重力mg、斜面的支持力FN和细线的拉力FT,则由平衡条件得:
斜面方向:mgsin α=FTcos θ ①
垂直斜面方向:FN+FTsin θ=mgcos α ②
使小球沿斜面缓慢下移时,θ减小,其他量不变,由①式知,FT变小.
由②知,FN变大,故A错误,B正确;
对斜面体进行受力分析,如图乙所示,斜面体受到重力Mg、地面的支持力FN地、地面的静摩擦力Ff和小球的压力FN′,由平衡条件得:
Ff=FN′sin α,FN′=FN变大,Ff变大
FN地=Mg+FN′cos α,FN′=FN变大,FN地变大,根据牛顿第三定律得,斜面体对地面的压力也变大,故C、D正确.
练习12(2016河北唐山联考,4分)如图,放在桌面上的A、B、C三个物块重均为100 N,小球P重20 N,作用在B上的水平力F=20 N,整个系统静止,则( )
A.A和B之间的摩擦力是20 N
B.B和C之间的摩擦力是20 N
C.物块C受六个力作用
D.C与桌面间的摩擦力为20 N
答案 B
考向三相似三角形法(一个力大小方向都不变,另外两个力大小方向都变化)
例题1(2018河北五校联考,7,4分)如图所示,质量分布均匀的细棒中心为O点,O1为光滑铰链,O2为光滑定滑轮,O2在O1正上方,一根轻绳一端系于O点,另一端跨过定滑轮O2由水平外力F牵引,用N表示铰链对杆的作用力,现在外力F作用下,细棒从图示位置缓慢转到竖直位置的过程中,下列说法正确的是( )
A.F逐渐变小,N大小不变
B.F逐渐变小,N大小变大
C.F先变小后变大,N逐渐变小
D.F先变小后变大,N逐渐变大
答案 A
练习1(2017重庆十一中月考,3,4分)如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔。质量为m的小球套在圆环上,一根细线的下端系着小球,上端穿过小孔用手拉住。现拉动细线,使小球沿圆环缓慢上移,在移动过程中手对线的拉力F和环对小球的弹力FN的大小变化情况是( )
A.F减小,FN不变 B.F不变,FN减小
C.F不变,FN增大 D.F增大,FN减小
答案 A
练习2表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比m1:m2为(不计球的大小)( )
A.24:1 B.25:1 C.24:25 D.25:24
答案 D
【解答】解:先以左侧小球为研究对象,分析受力情况:重力m1g、绳子的拉力T和半球的支持力N,作出力图。
由平衡条件得知,拉力T和支持力N的合力与重力mg大小相等、方向相反。设OO′=h,根据三角形相似得:
解得:
m1g=…①
同理,以右侧小球为研究对象,得:
m2g=…②
由①:②得
m1:m2=l2:l1=25:24
故选:D。
练习3如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )
A.绳子拉力不变 B.绳子拉力减小
C.AB杆受力增大 D.AB杆受力不变
答案 BD
考向四内接三角形法
例题1 (多选)(2017·全国卷Ⅰ·21)如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N,初始时,OM竖直且MN被拉直,OM与MN之间的夹角为α(α>).现将重物向右上方缓慢拉起,并保持夹角α不变.在OM由竖直被拉到水平的过程中( )
A.MN上的张力逐渐增大 B.MN上的张力先增大后减小
C.OM上的张力逐渐增大 D.OM上的张力先增大后减小
答案 AD
解析 以重物为研究对象,受重力mg、OM绳上拉力F2、MN上拉力F1,由题意知,三个力的合力始终为零,矢量三角形如图所示,F1、F2的夹角为π-α不变,在F2转至水平的过程中,矢量三角形在同一外接圆上,由图可知,MN上的张力F1逐渐增大,OM上的张力F2先增大后减小,所以A、D正确,B、C错误.
练习1如图所示,重为G的物体用两根绳子OA、OB悬挂,开始时绳OA水平,现将两绳同时顺时针缓慢转过90°,始终保持α角大小不变,且物体始终静止,绳OA的拉力为T1,绳OB的拉力为T2,则在此旋转过程中不可能发生的是( )
A.T1先减小后增大
B.T1先增大后减小
C.T2逐渐减小
D.T2最终变为零
答案 A
练习2如图所示,水平面上等腰三角形均匀框架顶角∠BAC=30°,一均匀圆球放在框架内,球与框架BC、AC两边接触但无挤压,现使框架以顶点A为转轴在竖直平面内顺时针方向从AB边水平缓慢转至AB边竖直,则在转动过程中( )
A.球对AB边的压力先增大后减小
B.球对BC边的压力先增大后减小
C.球对AC边的压力先增大后减小
D.球的重力势能一直增大
答案 AD
考向五利用正交分解、三角函数处理平衡问题
例题1(多选)如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过细绳跨过光滑的定滑轮与沙漏a连接,连接b的一段细绳与斜面平行.在a中的沙子缓慢流出的过程中,a、b、c都处于静止状态,则( )
A.b对c的摩擦力一定减小
B.b对c的摩擦力方向可能平行斜面向上
C.地面对c的摩擦力方向一定向右
D.地面对c的摩擦力一定减小
答案 BD
解析 设a、b的重力分别为Ga、Gb.若Ga=Gbsin θ,b受到c的摩擦力为零;若Ga≠Gbsin θ,b受到c的摩擦力不为零.若Ga>Gbsin θ,b受到c的摩擦力沿斜面向下,则b对c的摩擦力方向沿斜面向上,故A错误,B正确.以b、c整体为研究对象,受力分析如图,根据平衡条件得知地面对c的摩擦力Ff=FTcos θ=Gacos θ,方向水平向左.在a中的沙子缓慢流出的过程中,Ga减小,摩擦力减小.故D正确,C错误.
练习1如图所示,有一倾角θ=30°的斜面体B,质量为M.质量为m的物体A静止在B上.现用水平力F推物体A,在F由零逐渐增加到mg再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )
A.地面对B的支持力大于(M+m)g
B.A对B的压力的最小值为mg,最大值为mg
C.A所受摩擦力的最小值为0,最大值为
D.A所受摩擦力的最小值为mg,最大值为mg
答案 B
解析 因为A、B始终保持静止,对A、B整体受力分析可知,地面对B的支持力一直等于(M+m)g,A错误.当F=0时,A对B的压力最小,为mgcos 30°=mg;当F=mg时,A对B的压力最大,为mgcos 30°+Fsin 30°=mg,B正确.当Fcos 30°=mgsin 30°时,即F=mg时,A所受摩擦力为0,当F=0时,A所受摩擦力大小为mg,方向沿斜面向上,当F=mg时,A所受摩擦力大小为mg,方向沿斜面向下,选项C、D错误.
例题2(多选)如图所示,一光滑的轻滑轮用细绳OO′悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
A.绳OO′的张力也在一定范围内变化
B.物块b所受到的支持力也在一定范围内变化
C.连接a和b的绳的张力也在一定范围内变化
D.物块b与桌面间的摩擦力也在一定范围内变化
答案 BD
解析 由于物块a、b均保持静止,各绳角度保持不变,对a受力分析得,绳的拉力FT=mag,所以物块a受到绳的拉力保持不变.由滑轮性质,滑轮两侧绳的拉力相等,所以b受到绳的拉力大小、方向均保持不变,C选项错误;a、b受到绳的拉力大小、方向均不变,所以OO′的张力不变,A选项错误;对b进行受力分析,如图所示.由平衡条件得:FTcos β+Ff=Fcos α,Fsin α+FN+FTsin β=mbg.其中FT和mbg始终不变,当F大小在一定范围内变化时,支持力在一定范围内变化,B选项正确;摩擦力也在一定范围内发生变化,D选项正确.
练习3(2017·全国卷Ⅲ·17)一根轻质弹性绳的两端分别固定在水平天花板上相距80 cm的两点上,弹性绳的原长也为80 cm.将一钩码挂在弹性绳的中点,平衡时弹性绳的总长度为100 cm;再将弹性绳的两端缓慢移至天花板上的同一点,则弹性绳的总长度变为(弹性绳的伸长始终处于弹性限度内)( )
A.86 cm B.92 cm C.98 cm D.104 cm
答案 B
解析 设弹性绳的劲度系数为k.挂钩码后,弹性绳两端点移动前,绳的伸长量ΔL=100 cm-80 cm=20 cm,两段绳的弹力F=kΔL,对钩码受力分析,如图甲所示,sin α=,cos α=.根据共点力的平衡条件可得,钩码的重力为G=2kΔLcos α.将弹性绳的两端缓慢移至天花板上的同一点时,受力图如图乙所示.设弹性绳伸长量为ΔL′,弹力为F′=kΔL′,钩码的重力为G=2kΔL′,联立解得ΔL′=ΔL=12 cm.弹性绳的总长度变为L0+ΔL′=92 cm,故B正确,A、C、D错误.
甲 乙
练习4(多选)(2017·天津理综·8)如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态.如果只人为改变一个条件,当衣架静止时,下列说法正确的是( )
A.绳的右端上移到b′,绳子拉力不变
B.将杆N向右移一些,绳子拉力变大
C.绳的两端高度差越小,绳子拉力越小
D.若换挂质量更大的衣服,则衣架悬挂点右移
答案 AB
解析 设两杆间距离为d,绳长为l,Oa、Ob段长度分别为la和lb,则l=la+lb,两部分绳子与竖直方向夹角分别为α和β,受力分析如图所示.绳子中各部分张力相等,FTa=FTb=FT,则α=β.满足2FTcos α=mg,d=lasin α+lbsin α=lsin α,即sin α=,FT=,d和l均不变,则sin α为定值,α为定值,cos α为定值,绳子的拉力保持不变,故A正确,C错误;将杆N向右移一些,d增大,则sin α增大,cos α减小,绳子的拉力增大,故B正确;若换挂质量更大的衣服,d和l均不变,绳中拉力增大,但衣服的位置不变,D错误.
练习5(多选)如图所示,在固定好的水平和竖直的框架上,A、B两点连接着一根绕过光滑的轻小滑轮的不可伸长的细绳,重物悬挂于滑轮下,处于静止状态.若按照以下的方式缓慢移动细绳的端点,则下列判断正确的是( )
A.只将绳的左端移向A′点,拉力变小
B.只将绳的左端移向A′点,拉力不变
C.只将绳的右端移向B′点,拉力变小
D.只将绳的右端移向B′点,拉力变大
答案 BD
解析 设滑轮两侧绳子与竖直方向的夹角为α,绳子的长度为L,B点到墙壁的距离为s,根据几何知识和对称性,得:sin α= ①
以滑轮为研究对象,设绳子拉力大小为FT,根据平衡条件得:2FTcos α=mg,
得FT= ②
当只将绳的左端移向A′点,s和L均不变,则由②式知,FT不变,故A错误,B正确.当只将绳的右端移向B′点,s增加,而L不变,则由①式知,α增大,cos α减小,则由②式知,FT增大.故C错误,D正确.故选B、D.
练习6(2017·河北冀州2月模拟)如图所示,质量为m(可以看成质点)的小球P,用两根轻绳OP和O′P在P点拴结后再分别系于竖直墙上相距0.4 m的O、O′两点上,绳OP长0.5 m,绳O′P长0.3 m,今在小球上施加一方向与水平成θ=37°角的拉力F,将小球缓慢拉起.绳O′P刚拉直时,OP绳拉力为FT1,绳OP刚松弛时,O′P绳拉力为FT2,则FT1∶FT2为(sin 37°=0.6,cos 37°=0.8)( )
A.3∶4 B.4∶3 C.3∶5 D.4∶5
答案 C
解析 绳O′P刚拉直时,由几何关系可知此时OP绳与竖直方向夹角为37°,小球受力如图甲,则FT1=mg.绳OP刚松弛时,小球受力如图乙,则FT2=mg.则FT1∶FT2=3∶5,C选项正确.
练习7(多选)(2017·江西南昌3月模拟)如图所示,静止在粗糙水平面上的半径为4R的半球的最高点A处有一根水平细线系着质量为m、半径为R的光滑小球.已知重力加速度为g.下列说法正确的是( )
A.地面对半球的摩擦力的方向水平向右
B.细线对小球的拉力大小为mg
C.保持小球的位置不变,将A点沿半球逐渐下移,半球对小球的支持力逐渐减小
D.剪断细线的瞬间,小球的加速度大小为0.6g
答案 BD
解析 以半球和小球整体为研究对象,整体处于平衡状态,不受摩擦力作用,A项错误.对小球受力分析如图,拉力FTA=mgtan θ,由几何关系可知tan θ=,则FTA=mg,B项正确.半球对小球的支持力FN=,在A点下移时,θ增大,cos θ减小,则FN增大,C项错误.在剪断细线的瞬间,细线对小球的拉力消失,小球在沿切线方向有mgsin θ=ma,其中sin θ=0.6,得a=0.6g,D项正确.
练习8如图所示,物体A、B置于水平地面上,与地面间的动摩擦因数均为0.5,物体A、B用跨过光滑轻质动滑轮的细绳相连,现用逐渐增大的力斜向上提动滑轮,某时刻拉A物体的绳子与水平面成53°角,拉B物体的绳子与水平面成37°角,A、B两个物体仍处于平衡状态,此时若继续增大向上的力,A、B两个物体将同时开始运动,则A、B两个物体的质量之比为(认为最大静摩擦力等于滑动摩擦力,sin 37°=0.6,cos 37°=0.8,g=10 m/s2)( )
A. B. C. D.
答案 B
解析 对A、B两物体,由平衡条件得FTcos 53°=μ(mAg-FTsin 53°),FTcos 37°=μ(mBg-FTsin 37°),解得=,选项A、C、D错误,选项B正确.
练习9(2017·南京三模)小明家阁楼顶有一扇倾斜的天窗,天窗与竖直面的夹角为θ,如图所示,小明用质量为m的刮擦器擦天窗玻璃,当对刮擦器施加竖直向上大小为F的推力时,刮擦器恰好沿天窗玻璃向上匀速滑动,已知玻璃与刮擦器之间的动摩擦因数为μ,则刮擦器受到的摩擦力大小是( )
A.(F-mg)cosθ B.(F+mg)sinθ
C.μ(F-mg)cosθ D.μ(F+mg)sinθ
答案 A
解析 刮擦器受重力、推力、斜壁的弹力及摩擦力而处于平衡状态,
由图可知,F一定大于重力;
先将重力及向上的推力合力后,将二者的合力向垂直于斜面方向及沿斜面方向分解可得:
在沿斜面方向有:摩擦力f=(F-mg)cosθ;
在垂直斜面方向上有:FN=(F-mg)sinθ;
则f=(F-mg)cosθ=μ(F-mg)sinθ.
练习10(2017·深圳市调研)如图,一个轻型衣柜放在水平地面上,一条光滑轻绳两端分别固定在两侧顶端A、B上,再挂上带有衣服的衣架.若保持绳长和左端位置点不变,将右端依次改在C点或D点后固定,衣柜一直不动,下列说法正确的是( )
A.若改在C点,绳的张力大小不变
B.若改在D点,衣架两侧绳的张力不相等
C.若改在D点,衣架两侧绳的张力相等且不变
D.若改在C点,衣柜对地面的压力将会增大
答案 C
解析 对挂钩受力分析,根据平衡条件结合几何关系列式求解绳子拉力大小与重力的关系;分析绳子左右移动或上下移动时,细线与杆的夹角是否变化,由此分析拉力是否变化;整体为研究对象分析对地面的压力.
设绳子与竖直方向的夹角为θ,绳子张力为T,衣服的质量为m;根据共点力的平衡条件可得:2Tcosθ=mg,若改在C点,绳子与竖直方向的夹角变小,绳的张力变小,A项错误;若改在D点,衣架两侧绳的张力仍相等,B项错误;绳两端分别固定在两侧顶端A、B上时,受力情况如图所示,
设绳长为L,晾衣架宽度为d,根据几何关系可得sinθ=,当绳子右端上下移动过程中,绳子与竖直方向的夹角不变;则根据2Tcosθ=mg可知绳子拉力不变,C项正确;若改在C点,衣柜对地面的压力等于整体的重力,不变,D项错误.
练习11(2017·合肥市模拟)如图所示,质量M=2 kg的木块套在水平固定杆上,并用轻绳与质量m=1 kg的小球相连,今用跟水平方向成60°角的力F=10 N拉着小球并带动木块一起向右匀速运动,运动中M、m的相对位置保持不变,g=10 m/s2.在运动过程中,求:
(1)轻绳与水平方向的夹角.
(2)木块M与水平杆间的动摩擦因数μ.
答案 (1)θ=30° (2)μ=
解析 以m为研究对象,由平衡条件得:
水平方向Fcos60°-FTcosθ=0 ①
竖直方向Fsin60°-FTsinθ-mg=0 ②
解得:θ=30°
(2)以M、m整体为研究对象.由平衡条件得:
水平方向Fcos60°-μFN=0 ③
竖直方向FN+Fsin60°-Mg-mg=0 ④
由③④得μ=.
练习12如图所示,物体的质量为2 kg,两根轻细绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使绳都能伸直,求拉力F的大小范围.(g取10 m/s2)
答案 10 N≤F≤20 N
解析 对A球受力分析,受到拉力F,重力mg,两根细绳的拉力FB、FC,
如图所示,根据平衡条件,有:
x方向:Fcos60°=FCcos30°+FBcos30°
y方向:Fsin60°+FBsin30°=mg+FCsin30°
解得:FB=mg-F FC=F-mg
当FB=0时,F最大,为:Fmax=20 N;
当FC=0时,F最小,为:F min=10 N;
故拉力F的范围为:10 N≤F≤20 N.
练习13质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在木楔斜面上时,它正好匀速下滑.如果用与木楔斜面成α角的力F拉着木块匀速上升,如图所示(已知木楔在整个过程中始终静止).
(1)当α=θ时,拉力F有最小值,求此最小值;
(2)当α=θ时,木楔对水平面的摩擦力是多大?
答案 (1)mgsin 2θ (2)mgsin 4θ
解析 木块在木楔斜面上匀速向下运动时,有
mgsin θ=μmgcos θ,
即μ=tan θ.
(1)木块在力F作用下沿斜面向上匀速运动,有
Fcos α=mgsin θ+Ff
Fsin α+FN=mgcos θ
Ff=μFN
解得F===
则当α=θ时,F有最小值,为Fmin=mgsin 2θ.
(2)因为木块及木楔均处于平衡状态,整体受到地面的摩擦力等于F的水平分力,即Ff=Fcos (α+θ)
当α=θ时,F取最小值mgsin 2θ,
Ffm=Fmincos 2θ=mg·sin 2θcos 2θ=mgsin 4θ.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
