2019年沪科新版九年级上册数学第22章相似形单元测试卷(解析版)
文档属性
| 名称 | 2019年沪科新版九年级上册数学第22章相似形单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 14:18:24 | ||
图片预览


文档简介
2019年沪科新版九年级上册数学《第22章 相似形》单元测试卷
一.选择题(共10小题)
1.如果3a=2b(ab≠0),那么比例式中正确的是( )
A.= B.= C.= D.=
2.下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
3.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
4.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
5.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
6.如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
A.6.4cm B.6cm C.2cm D.4cm
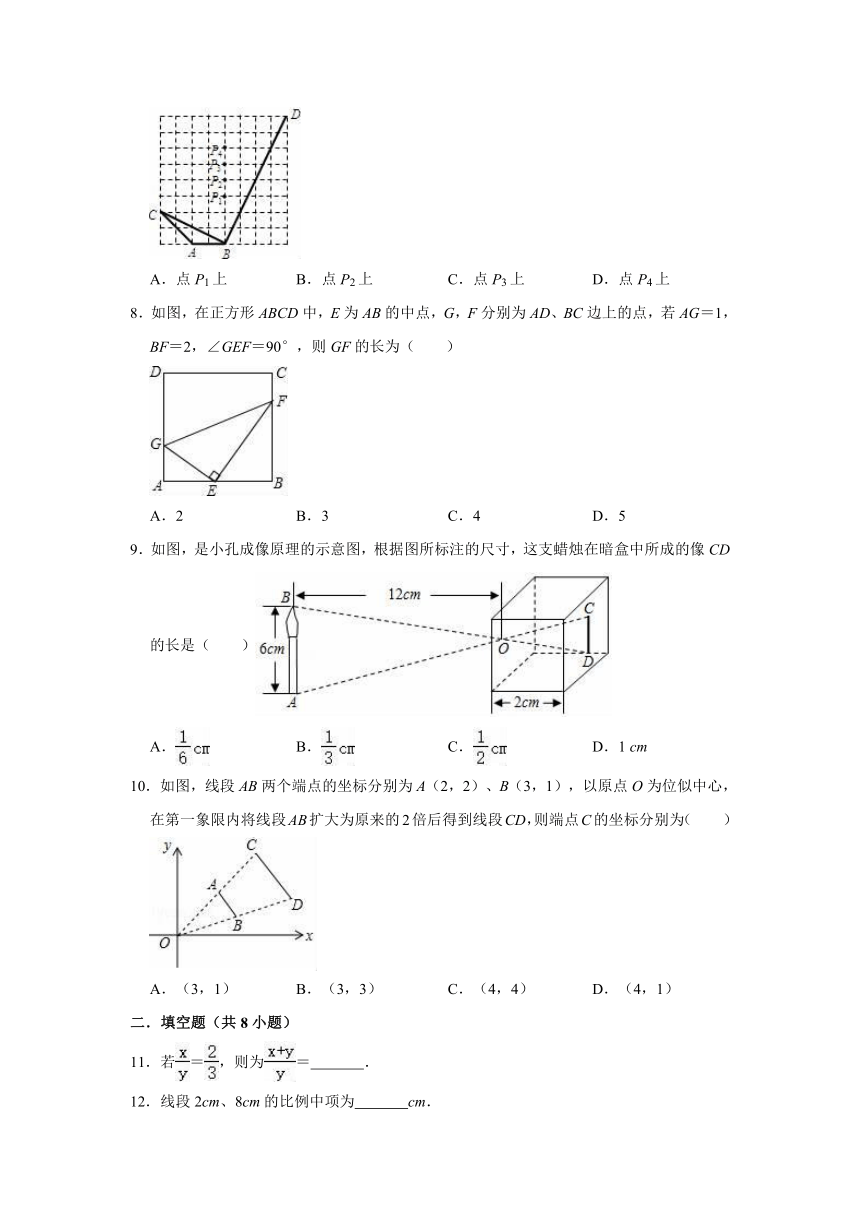
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上 B.点P2上 C.点P3上 D.点P4上
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD、BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.2 B.3 C.4 D.5
9.如图,是小孔成像原理的示意图,根据图所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. B. C. D.1 cm
10.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(3,1) B.(3,3) C.(4,4) D.(4,1)
二.填空题(共8小题)
11.若=,则为= .
12.线段2cm、8cm的比例中项为 cm.
13.点C是线段AB的黄金分割点(AC>BC),AB=2,则AC= .(用根号表示)
14.如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= .
15.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
16.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连结EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
17.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 .
18.一副三角板叠放如图,则△AOB与△DOC的面积之比为 .
三.解答题(共8小题)
19.已知,求下列算式的值.
(1);
(2).
20.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
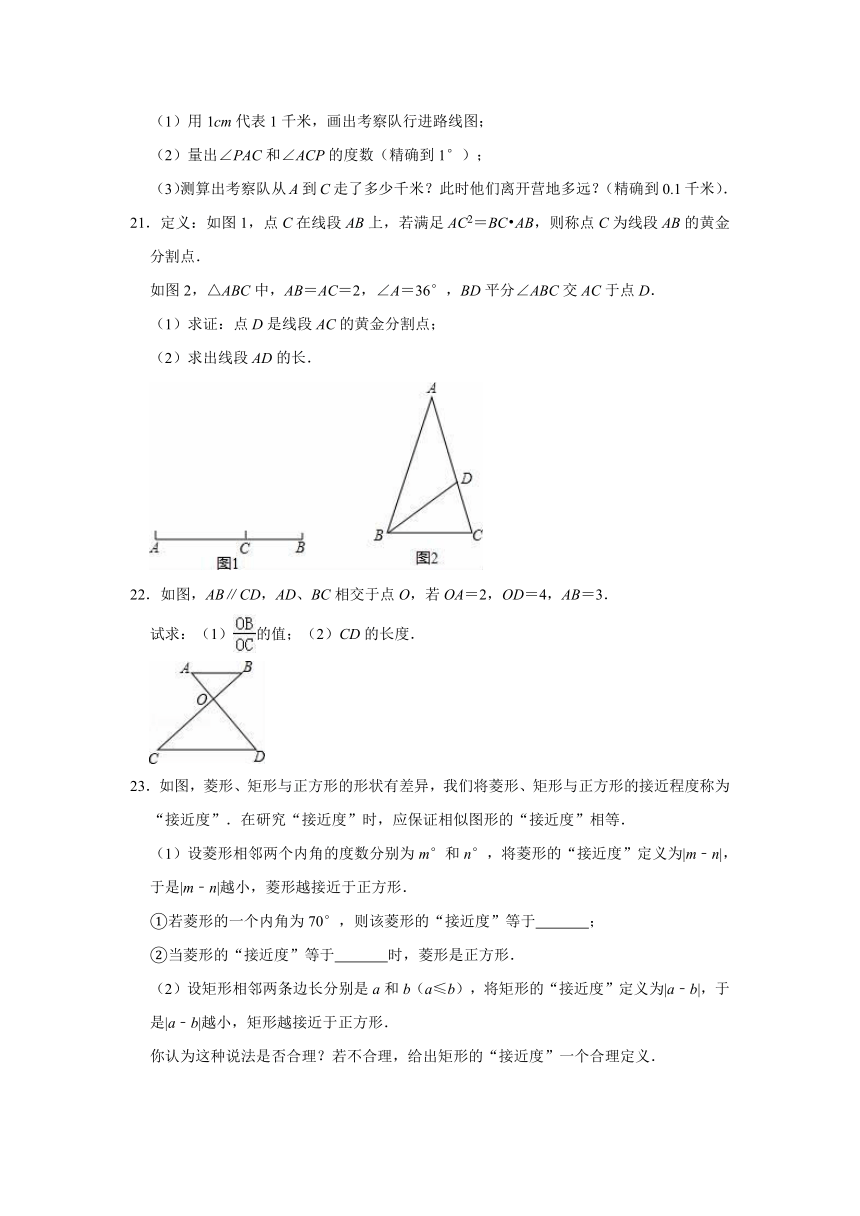
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
21.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
22.如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
试求:(1)的值;(2)CD的长度.
23.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
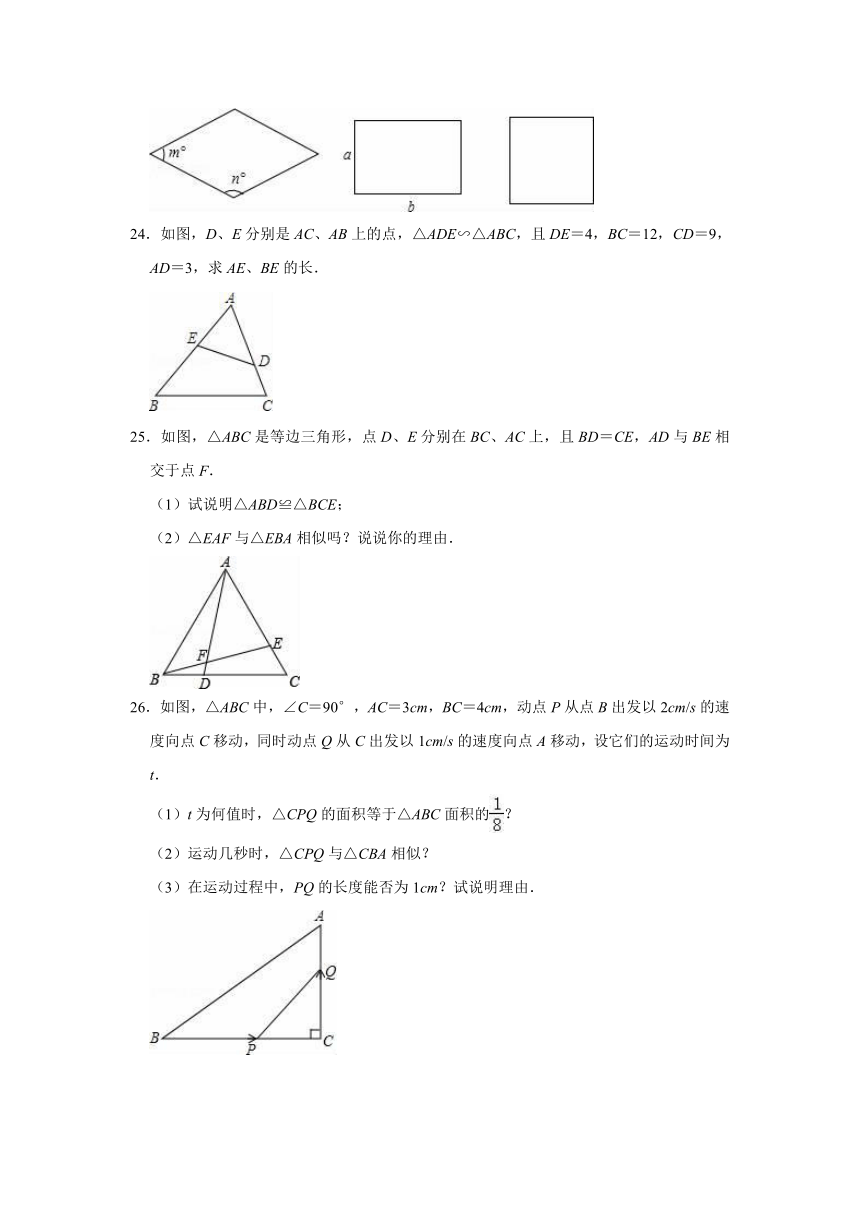
24.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
25.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
26.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
2019年沪科新版九年级上册数学《第22章 相似形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如果3a=2b(ab≠0),那么比例式中正确的是( )
A.= B.= C.= D.=
【分析】先逆用比例的基本性质,把3a=2b改写成比例的形式,使相乘的两个数a和3做比例的外项,则相乘的另两个数b和2就做比例的内项;进而判断得解.
【解答】解:∵3a=2b,
∴a:b=2:3,b:a=3:2,
即a:2=b:3,
故A,B均错误,C正确,D错误.
故选:C.
【点评】本题主要考查了比例的性质,解答此题的关键是比例基本性质的逆运用,要注意:内项之积等于外项之积.本题也可以将各选项中的比例式化为等积式进行判断.
2.下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.×3≠2×,故本选项错误;
B.4×10≠5×6,故本选项错误;
C.2×=×2,故本选项正确;
D.4×1≠3×2,故本选项错误;
故选:C.
【点评】此题考查了比例线段,理解成比例线段的概念和变形是解题的关键,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
3.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
【分析】由于点C是线段AB的黄金分割点(AC>BC),根据黄金分割的定义得到AC=AB,然后把AB=10cm代入计算即可.
【解答】解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=AB,
而AB=10cm,
∴AC=×10=5(﹣1)cm.
故选:C.
【点评】本题考查了黄金分割的定义:线段上一点把线段分成两段,其中较长线段是较短线段和整个线段的比例中项,即较长线段是整个线段的倍,那么这个点就是这条线段的黄金分割点.
4.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
【分析】三条平行线截两条直线,所得的对应线段成比例.
【解答】解:∵AB∥CD∥EF,
∴,
∴BE===10,
∴CE=BE﹣BC=10﹣6=4,
故选:B.
【点评】本题考查了平行线分线段成比例,正确列出比例式是解题的关键.
5.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
【分析】根据相似图形的形状必须完全相同;相似图形的大小不一定相同进行分析即可.
【解答】解:A、两个平行四边形一定相似,说法错误;
B、两个菱形一定相似,说法错误;
C、两个矩形一定相似,说法错误;
D、两个等腰直角三角形一定相似,说法正确;
故选:D.
【点评】此题主要考查了相似图形,关键是掌握相似图形定义:把形状相同的图形称为相似形.
6.如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
A.6.4cm B.6cm C.2cm D.4cm
【分析】由△ABC∽△ACD,且AB=10cm,AC=8cm,根据相似三角形的对应边成比例,即可求得答案.
【解答】解:∵△ABC∽△ACD,
∴,
∵AB=10cm,AC=8cm,
∴,
∴AD=6.4.
故选:A.
【点评】此题考查了相似三角形的性质.注意相似三角形的对应边成比例.
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上 B.点P2上 C.点P3上 D.点P4上
【分析】由图可知∠BPD一定是钝角,若要△ABC∽△PBD,则PB、PD与AB、AC的比值必须相等,可据此进行判断.
【解答】解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC=2,
∴BA:AC=1:,
∴BP:PD=1:或BP:PD=:1,
只有P2符合这样的要求,故P点应该在P2.
故选:B.
【点评】此题考查了相似三角形的性质,以及勾股定理的运用,相似三角形的对应角相等,对应边成比例,书写相似三角形时,对应顶点要对应.熟练掌握相似三角形的性质是解本题的关键.
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD、BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.2 B.3 C.4 D.5
【分析】由在正方形ABCD中,∠GEF=90°,易证得△AGE∽△BEF,又由E为AB的中点,AG=1,BF=2,根据相似三角形的对应边成比例,易求得AE与BE的长,然后由勾股定理求得答案.
【解答】解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠GEF=90°,
∴∠AEG+∠BEF=90°,
∴∠AGE=∠BEF,
∴△AGE∽△BEF,
∴,
∵E为AB的中点,
∴AE=BE,
∵AG=1,BF=2,
∴,
解得:BE=AE=,
在Rt△AEG中,GE2=AG2+AE2=3,
在Rt△BEF中,EF2=BE2+BF2=6,
∴在Rt△GEF中,GF==3.
故选:B.
【点评】此题考查了相似三角形的判定与性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.
9.如图,是小孔成像原理的示意图,根据图所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. B. C. D.1 cm
【分析】据小孔成像原理可知△AOB∽△COD,利用它们的对应边成比例就可以求出CD之长.
【解答】解:如图过O作直线OE⊥AB,交CD于F,
依题意AB∥CD
∴OF⊥CD
∴OE=12,OF=2
而AB∥CD可以得△AOB∽△COD
∵OE,OF分别是它们的高
∴,
∵AB=6,
∴CD=1,
故选:D.
【点评】本题考查了相似三角形的应用,解题的关键在于理解小孔成像原理给我们带来的已知条件,还有会用相似三角形对应边成比例.
10.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(3,1) B.(3,3) C.(4,4) D.(4,1)
【分析】利用位似图形的性质结合对应点坐标与位似比的关系得出C点坐标.
【解答】解:∵以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,
∴A点与C点是对应点,
∵C点的对应点A的坐标为(2,2),位似比为:1:2,
∴点C的坐标为:(4,4)
故选:C.
【点评】此题主要考查了位似变换,正确把握位似比与对应点坐标的关系是解题关键.
二.填空题(共8小题)
11.若=,则为= .
【分析】由=,可以假设x=2k,y=3k,代入计算即可解决问题.
【解答】解:∵=,
∴可以假设x=2k,y=3k,
∴===.
故答案为.
【点评】本题考查比例的性质,解题的关键是学会利用参数解决问题,属于中考常考题型.
12.线段2cm、8cm的比例中项为 4 cm.
【分析】比例的基本性质:两外项之积等于两内项之积.
【解答】解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=2×8,x=±4(线段是正数,负值舍去),故填4.
【点评】理解比例中项的概念,注意:求两条线段的比例中项的时候,应舍去负数.
13.点C是线段AB的黄金分割点(AC>BC),AB=2,则AC= ﹣1+ .(用根号表示)
【分析】用AC表示出BC,然后根据黄金分割点的定义列方程求解即可.
【解答】解:∵AC>BC,AB=2,
∴BC=AB﹣AC=2﹣AC,
∵点C是线段AB的黄金分割点,
∴AC2=AB?BC,
∴AC2=2(2﹣AC),
整理得,AC2+2AC﹣4=0,
解得AC=﹣1+,AC=﹣1﹣(舍去).
故答案为:﹣1+.
【点评】本题考查了黄金分割,熟记黄金分割点的定义并列出关于AC的方程是解题的关键.
14.如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= 8:5 .
【分析】如图,过点D作DF∥BE交AC于点F.由平行线分线段成比例和比例的性质求得EF:FC=BD:DC=2:3.AM:MD=AE:EF=4:1,由此求得AE:EC=8:5.
【解答】解:如图,过点D作DF∥BE交AC于点F.
∴EF:FC=BD:DC,AM:MD=AE:EF.
∵BD:DC=2:3,
∴EF:FC=BD:DC=2:3.
设EF=2a,则CF=3a.
∵AM:MD=AE:EF,
∵AM:MD=4:1
∴AE:EF=4:1
∴AE=8a
∴AE:EC=8a:5a=8:5.
故答案是:8:5.
【点评】本题考查平行线分线段成比例定理.解题时,用平行线分线段成比例定理以及比例的性质进行变形即可得到答案.
15.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 5 倍.
【分析】由题意一个三角形的各边长扩大为原来的5倍,根据相似三角形的性质及对应边长成比例来求解.
【解答】解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
【点评】本题考查了相似三角形的性质:相似三角形的周长的比等于相似比.
16.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连结EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 10 .
【分析】依据BD=AB,BE是∠ABC的平分线,即可得到AE=DE,进而得出△BDE的面积与△ABE的面积均为3,再根据EF是△ACD的中位线,即可得出△ACD的面积为4,即可得到△ABC的面积为3+3+4=10.
【解答】解:∵BD=AB,BE是∠ABC的平分线,
∴AE=DE,
∴△BDE的面积与△ABE的面积均为3,
又∵点F是AC的中点,
∴EF是△ACD的中位线,
∴2EF=CD,EF∥DC,
∴△AEF∽△ADC,
∴S△ACD=4S△AEF,
∵四边形CDEF的面积为3,
∴△ACD的面积为4,
∴△ABC的面积为3+3+4=10.
故答案为:10.
【点评】本题主要考查了三角形中位线定理以及相似三角形的判定与性质,相似三角形的面积的比等于相似比的平方.
17.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 ∠ABP=∠C或∠APB=∠ABC或AB2=AP?AC .
【分析】根据相似三角形的判定方法,即可解决问题.
【解答】解:在△ABP和△ACB中,
∵∠A=∠A,
∴当∠ABP=∠C或∠APB=∠ABC或=即AB2=AP?AC时,
△ABP∽△ACB,
故答案为∠ABP=∠C或∠APB=∠ABC或AB2=AP?AC.
【点评】本题考查相似三角形的判定,解题的关键是记住相似三角形的判定方法,属于基础题中考常考题型.
18.一副三角板叠放如图,则△AOB与△DOC的面积之比为 .
【分析】,设BC=a,求出AB、CD,由△AOB∽△COD,得=()2即可解决问题.
【解答】解:设BC=a,
在Rt△ABC中,AB=BC=a,
在Rt△BCD中,∵DC=BC,
∴CD=a,
∵∠ABC+∠BCD=180°,
∴AB∥CD,
∴△AOB∽△COD,
∴=()2=()2=,
故答案为.
【点评】本题考查相似三角形的判定和性质、特殊三角形的边角关系等知识,解题的关键是应用了相似三角形的面积比等于相似比的平方,属于常见题,中考常考题型.
三.解答题(共8小题)
19.已知,求下列算式的值.
(1);
(2).
【分析】(1)由比例的性质容易得出结果;
(2)设a=3k,则b=2k,代入计算化简即可.
【解答】解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
【点评】本题考查了比例的性质,代数式的求值;熟练掌握比例的性质是解决问题的关键.
20.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
【分析】(1)先画出方向标,再确定方位角、比例尺作图;
(2)动手操作利用量角器测量即可;
(3)先利用刻度尺测量出图上距离,再根据比例尺换算成实际距离.
【解答】解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
【点评】主要考查了方位角的作图能力.要会根据比例尺准确的作图,并根据图例测算出实际距离.
21.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
【分析】(1)判断△ABC∽△BDC,根据对应边成比例可得出答案.
(2)根据黄金比值即可求出AD的长度.
【解答】解:(1)∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD,BC=BD,
∴△ABC∽△BDC,
∴=,即=,
∴AD2=AC?CD.
∴点D是线段AC的黄金分割点.
(2)∵点D是线段AC的黄金分割点,
∴AD=AC,
∵AC=2,
∴AD=﹣1.
【点评】本题考查了黄金分割的知识,解答本题的关键是仔细审题,理解黄金分割的定义,注意掌握黄金比值.
22.如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
试求:(1)的值;(2)CD的长度.
【分析】(1)根据平行线分线段定理,由AB∥CD,即可得出===;
(2)根据平行线分线段定理,由AB∥CD,即可得出=,进而求得CD的长度.
【解答】解:(1)∵AB∥CD,
∴===;
(2)∵AB∥CD,
∴=,
∵OA=2,OD=4,AB=3.
∴CD==6.
【点评】本题考查了平行线分线段定理,熟练掌握性质定理是本题的关键.
23.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 40 ;
②当菱形的“接近度”等于 0 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;
(2)不合理,举例进行说明.
【解答】解:(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.
24.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
【分析】由△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,根据相似三角形的对应边成比例,即可求得答案.
【解答】解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴AE=4,AB=9,
∴BE=AB﹣AE=5.
【点评】此题考查了相似三角形的性质.注意掌握相似三角形的对应边成比例定理的应用是解此题的关键.
25.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
【分析】(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;
(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE,进而可以求得∠EAF=∠EBA,即可求证△EAF∽△EBA,即可解题.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
【点评】本题考查了全等三角形的判定和全等三角形对应角相等的性质,考查了相似三角形的判定,考查了等边三角形各边长相等、各内角为60°的性质.
26.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
【分析】(1)根据三角形的面积列方程即可求出结果;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,①若Rt△ABC∽Rt△QPC,②若Rt△ABC∽Rt△PQC,然后列方程求解;
(3)根据勾股定理列方程,此方程无解,于是得到在运动过程中,PQ的长度能否为1cm.
【解答】解:(1)经过t秒后,PC=4﹣2t,CQ=t,
当△CPQ的面积等于△ABC面积的时,
即(4﹣2t)?t=××3×4,
解得;t=或t=;
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若Rt△ABC∽Rt△QPC则=,即=,解之得t=1.2;
②若Rt△ABC∽Rt△PQC则=,=,解之得t=;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为1.2或秒;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
∵此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
【点评】本题考查了动点问题,相似三角形的判定和性质,三角形的面积,特别是(2)注意分类讨论.
一.选择题(共10小题)
1.如果3a=2b(ab≠0),那么比例式中正确的是( )
A.= B.= C.= D.=
2.下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
3.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
4.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
5.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
6.如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
A.6.4cm B.6cm C.2cm D.4cm
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上 B.点P2上 C.点P3上 D.点P4上
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD、BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.2 B.3 C.4 D.5
9.如图,是小孔成像原理的示意图,根据图所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. B. C. D.1 cm
10.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(3,1) B.(3,3) C.(4,4) D.(4,1)
二.填空题(共8小题)
11.若=,则为= .
12.线段2cm、8cm的比例中项为 cm.
13.点C是线段AB的黄金分割点(AC>BC),AB=2,则AC= .(用根号表示)
14.如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= .
15.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
16.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连结EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
17.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 .
18.一副三角板叠放如图,则△AOB与△DOC的面积之比为 .
三.解答题(共8小题)
19.已知,求下列算式的值.
(1);
(2).
20.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
21.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
22.如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
试求:(1)的值;(2)CD的长度.
23.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
24.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
25.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
26.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
2019年沪科新版九年级上册数学《第22章 相似形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如果3a=2b(ab≠0),那么比例式中正确的是( )
A.= B.= C.= D.=
【分析】先逆用比例的基本性质,把3a=2b改写成比例的形式,使相乘的两个数a和3做比例的外项,则相乘的另两个数b和2就做比例的内项;进而判断得解.
【解答】解:∵3a=2b,
∴a:b=2:3,b:a=3:2,
即a:2=b:3,
故A,B均错误,C正确,D错误.
故选:C.
【点评】本题主要考查了比例的性质,解答此题的关键是比例基本性质的逆运用,要注意:内项之积等于外项之积.本题也可以将各选项中的比例式化为等积式进行判断.
2.下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d= B.a=4,b=6,c=5,d=10
C.a=2,b=,c=2,d= D.a=2,b=3,c=4,d=1
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.×3≠2×,故本选项错误;
B.4×10≠5×6,故本选项错误;
C.2×=×2,故本选项正确;
D.4×1≠3×2,故本选项错误;
故选:C.
【点评】此题考查了比例线段,理解成比例线段的概念和变形是解题的关键,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
3.点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A.6cm B.(5+1)cm C.5(﹣1)cm D.(5﹣1)cm
【分析】由于点C是线段AB的黄金分割点(AC>BC),根据黄金分割的定义得到AC=AB,然后把AB=10cm代入计算即可.
【解答】解:∵点C是线段AB的黄金分割点(AC>BC),
∴AC=AB,
而AB=10cm,
∴AC=×10=5(﹣1)cm.
故选:C.
【点评】本题考查了黄金分割的定义:线段上一点把线段分成两段,其中较长线段是较短线段和整个线段的比例中项,即较长线段是整个线段的倍,那么这个点就是这条线段的黄金分割点.
4.如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,CE的长为( )
A.2 B.4 C.3 D.5
【分析】三条平行线截两条直线,所得的对应线段成比例.
【解答】解:∵AB∥CD∥EF,
∴,
∴BE===10,
∴CE=BE﹣BC=10﹣6=4,
故选:B.
【点评】本题考查了平行线分线段成比例,正确列出比例式是解题的关键.
5.下列说法中正确的是( )
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
【分析】根据相似图形的形状必须完全相同;相似图形的大小不一定相同进行分析即可.
【解答】解:A、两个平行四边形一定相似,说法错误;
B、两个菱形一定相似,说法错误;
C、两个矩形一定相似,说法错误;
D、两个等腰直角三角形一定相似,说法正确;
故选:D.
【点评】此题主要考查了相似图形,关键是掌握相似图形定义:把形状相同的图形称为相似形.
6.如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )
A.6.4cm B.6cm C.2cm D.4cm
【分析】由△ABC∽△ACD,且AB=10cm,AC=8cm,根据相似三角形的对应边成比例,即可求得答案.
【解答】解:∵△ABC∽△ACD,
∴,
∵AB=10cm,AC=8cm,
∴,
∴AD=6.4.
故选:A.
【点评】此题考查了相似三角形的性质.注意相似三角形的对应边成比例.
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上 B.点P2上 C.点P3上 D.点P4上
【分析】由图可知∠BPD一定是钝角,若要△ABC∽△PBD,则PB、PD与AB、AC的比值必须相等,可据此进行判断.
【解答】解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC=2,
∴BA:AC=1:,
∴BP:PD=1:或BP:PD=:1,
只有P2符合这样的要求,故P点应该在P2.
故选:B.
【点评】此题考查了相似三角形的性质,以及勾股定理的运用,相似三角形的对应角相等,对应边成比例,书写相似三角形时,对应顶点要对应.熟练掌握相似三角形的性质是解本题的关键.
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD、BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A.2 B.3 C.4 D.5
【分析】由在正方形ABCD中,∠GEF=90°,易证得△AGE∽△BEF,又由E为AB的中点,AG=1,BF=2,根据相似三角形的对应边成比例,易求得AE与BE的长,然后由勾股定理求得答案.
【解答】解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠GEF=90°,
∴∠AEG+∠BEF=90°,
∴∠AGE=∠BEF,
∴△AGE∽△BEF,
∴,
∵E为AB的中点,
∴AE=BE,
∵AG=1,BF=2,
∴,
解得:BE=AE=,
在Rt△AEG中,GE2=AG2+AE2=3,
在Rt△BEF中,EF2=BE2+BF2=6,
∴在Rt△GEF中,GF==3.
故选:B.
【点评】此题考查了相似三角形的判定与性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.
9.如图,是小孔成像原理的示意图,根据图所标注的尺寸,这支蜡烛在暗盒中所成的像CD的长是( )
A. B. C. D.1 cm
【分析】据小孔成像原理可知△AOB∽△COD,利用它们的对应边成比例就可以求出CD之长.
【解答】解:如图过O作直线OE⊥AB,交CD于F,
依题意AB∥CD
∴OF⊥CD
∴OE=12,OF=2
而AB∥CD可以得△AOB∽△COD
∵OE,OF分别是它们的高
∴,
∵AB=6,
∴CD=1,
故选:D.
【点评】本题考查了相似三角形的应用,解题的关键在于理解小孔成像原理给我们带来的已知条件,还有会用相似三角形对应边成比例.
10.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(3,1) B.(3,3) C.(4,4) D.(4,1)
【分析】利用位似图形的性质结合对应点坐标与位似比的关系得出C点坐标.
【解答】解:∵以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,
∴A点与C点是对应点,
∵C点的对应点A的坐标为(2,2),位似比为:1:2,
∴点C的坐标为:(4,4)
故选:C.
【点评】此题主要考查了位似变换,正确把握位似比与对应点坐标的关系是解题关键.
二.填空题(共8小题)
11.若=,则为= .
【分析】由=,可以假设x=2k,y=3k,代入计算即可解决问题.
【解答】解:∵=,
∴可以假设x=2k,y=3k,
∴===.
故答案为.
【点评】本题考查比例的性质,解题的关键是学会利用参数解决问题,属于中考常考题型.
12.线段2cm、8cm的比例中项为 4 cm.
【分析】比例的基本性质:两外项之积等于两内项之积.
【解答】解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=2×8,x=±4(线段是正数,负值舍去),故填4.
【点评】理解比例中项的概念,注意:求两条线段的比例中项的时候,应舍去负数.
13.点C是线段AB的黄金分割点(AC>BC),AB=2,则AC= ﹣1+ .(用根号表示)
【分析】用AC表示出BC,然后根据黄金分割点的定义列方程求解即可.
【解答】解:∵AC>BC,AB=2,
∴BC=AB﹣AC=2﹣AC,
∵点C是线段AB的黄金分割点,
∴AC2=AB?BC,
∴AC2=2(2﹣AC),
整理得,AC2+2AC﹣4=0,
解得AC=﹣1+,AC=﹣1﹣(舍去).
故答案为:﹣1+.
【点评】本题考查了黄金分割,熟记黄金分割点的定义并列出关于AC的方程是解题的关键.
14.如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= 8:5 .
【分析】如图,过点D作DF∥BE交AC于点F.由平行线分线段成比例和比例的性质求得EF:FC=BD:DC=2:3.AM:MD=AE:EF=4:1,由此求得AE:EC=8:5.
【解答】解:如图,过点D作DF∥BE交AC于点F.
∴EF:FC=BD:DC,AM:MD=AE:EF.
∵BD:DC=2:3,
∴EF:FC=BD:DC=2:3.
设EF=2a,则CF=3a.
∵AM:MD=AE:EF,
∵AM:MD=4:1
∴AE:EF=4:1
∴AE=8a
∴AE:EC=8a:5a=8:5.
故答案是:8:5.
【点评】本题考查平行线分线段成比例定理.解题时,用平行线分线段成比例定理以及比例的性质进行变形即可得到答案.
15.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 5 倍.
【分析】由题意一个三角形的各边长扩大为原来的5倍,根据相似三角形的性质及对应边长成比例来求解.
【解答】解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
【点评】本题考查了相似三角形的性质:相似三角形的周长的比等于相似比.
16.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连结EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 10 .
【分析】依据BD=AB,BE是∠ABC的平分线,即可得到AE=DE,进而得出△BDE的面积与△ABE的面积均为3,再根据EF是△ACD的中位线,即可得出△ACD的面积为4,即可得到△ABC的面积为3+3+4=10.
【解答】解:∵BD=AB,BE是∠ABC的平分线,
∴AE=DE,
∴△BDE的面积与△ABE的面积均为3,
又∵点F是AC的中点,
∴EF是△ACD的中位线,
∴2EF=CD,EF∥DC,
∴△AEF∽△ADC,
∴S△ACD=4S△AEF,
∵四边形CDEF的面积为3,
∴△ACD的面积为4,
∴△ABC的面积为3+3+4=10.
故答案为:10.
【点评】本题主要考查了三角形中位线定理以及相似三角形的判定与性质,相似三角形的面积的比等于相似比的平方.
17.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 ∠ABP=∠C或∠APB=∠ABC或AB2=AP?AC .
【分析】根据相似三角形的判定方法,即可解决问题.
【解答】解:在△ABP和△ACB中,
∵∠A=∠A,
∴当∠ABP=∠C或∠APB=∠ABC或=即AB2=AP?AC时,
△ABP∽△ACB,
故答案为∠ABP=∠C或∠APB=∠ABC或AB2=AP?AC.
【点评】本题考查相似三角形的判定,解题的关键是记住相似三角形的判定方法,属于基础题中考常考题型.
18.一副三角板叠放如图,则△AOB与△DOC的面积之比为 .
【分析】,设BC=a,求出AB、CD,由△AOB∽△COD,得=()2即可解决问题.
【解答】解:设BC=a,
在Rt△ABC中,AB=BC=a,
在Rt△BCD中,∵DC=BC,
∴CD=a,
∵∠ABC+∠BCD=180°,
∴AB∥CD,
∴△AOB∽△COD,
∴=()2=()2=,
故答案为.
【点评】本题考查相似三角形的判定和性质、特殊三角形的边角关系等知识,解题的关键是应用了相似三角形的面积比等于相似比的平方,属于常见题,中考常考题型.
三.解答题(共8小题)
19.已知,求下列算式的值.
(1);
(2).
【分析】(1)由比例的性质容易得出结果;
(2)设a=3k,则b=2k,代入计算化简即可.
【解答】解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
【点评】本题考查了比例的性质,代数式的求值;熟练掌握比例的性质是解决问题的关键.
20.某考察队从营地P处出发,沿北偏东60°前进了5千米到达A地,再沿东南方向前进到达C地,C地恰好在P地的正东方向.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)量出∠PAC和∠ACP的度数(精确到1°);
(3)测算出考察队从A到C走了多少千米?此时他们离开营地多远?(精确到0.1千米).
【分析】(1)先画出方向标,再确定方位角、比例尺作图;
(2)动手操作利用量角器测量即可;
(3)先利用刻度尺测量出图上距离,再根据比例尺换算成实际距离.
【解答】解:(1)路线图(6分)(P、A、C点各2分)
注意:起点是必须在所给的图形中画,否则即使画图正确扣;(2分)
(2)量得∠PAC≈105°,∠ACP≈45°;(9分)(只有1个正确得2分)
(3)量路线图得AC≈3.5厘米,PC≈6.8厘米.
∴AC≈3.5千米;PC≈6.8千米(13分)
【点评】主要考查了方位角的作图能力.要会根据比例尺准确的作图,并根据图例测算出实际距离.
21.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
【分析】(1)判断△ABC∽△BDC,根据对应边成比例可得出答案.
(2)根据黄金比值即可求出AD的长度.
【解答】解:(1)∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,∠BDC=72°,
∴AD=BD,BC=BD,
∴△ABC∽△BDC,
∴=,即=,
∴AD2=AC?CD.
∴点D是线段AC的黄金分割点.
(2)∵点D是线段AC的黄金分割点,
∴AD=AC,
∵AC=2,
∴AD=﹣1.
【点评】本题考查了黄金分割的知识,解答本题的关键是仔细审题,理解黄金分割的定义,注意掌握黄金比值.
22.如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
试求:(1)的值;(2)CD的长度.
【分析】(1)根据平行线分线段定理,由AB∥CD,即可得出===;
(2)根据平行线分线段定理,由AB∥CD,即可得出=,进而求得CD的长度.
【解答】解:(1)∵AB∥CD,
∴===;
(2)∵AB∥CD,
∴=,
∵OA=2,OD=4,AB=3.
∴CD==6.
【点评】本题考查了平行线分线段定理,熟练掌握性质定理是本题的关键.
23.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 40 ;
②当菱形的“接近度”等于 0 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;
(2)不合理,举例进行说明.
【解答】解:(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.
24.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
【分析】由△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,根据相似三角形的对应边成比例,即可求得答案.
【解答】解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴AE=4,AB=9,
∴BE=AB﹣AE=5.
【点评】此题考查了相似三角形的性质.注意掌握相似三角形的对应边成比例定理的应用是解此题的关键.
25.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
【分析】(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;
(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE,进而可以求得∠EAF=∠EBA,即可求证△EAF∽△EBA,即可解题.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
【点评】本题考查了全等三角形的判定和全等三角形对应角相等的性质,考查了相似三角形的判定,考查了等边三角形各边长相等、各内角为60°的性质.
26.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
【分析】(1)根据三角形的面积列方程即可求出结果;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,①若Rt△ABC∽Rt△QPC,②若Rt△ABC∽Rt△PQC,然后列方程求解;
(3)根据勾股定理列方程,此方程无解,于是得到在运动过程中,PQ的长度能否为1cm.
【解答】解:(1)经过t秒后,PC=4﹣2t,CQ=t,
当△CPQ的面积等于△ABC面积的时,
即(4﹣2t)?t=××3×4,
解得;t=或t=;
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若Rt△ABC∽Rt△QPC则=,即=,解之得t=1.2;
②若Rt△ABC∽Rt△PQC则=,=,解之得t=;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为1.2或秒;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
∵此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
【点评】本题考查了动点问题,相似三角形的判定和性质,三角形的面积,特别是(2)注意分类讨论.
