2019年沪科新版九年级上册数学第23章解直角三角形单元测试卷(解析版)
文档属性
| 名称 | 2019年沪科新版九年级上册数学第23章解直角三角形单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 675.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-30 14:16:41 | ||
图片预览



文档简介
2019年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷
一.选择题(共10小题)
1.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
2.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
3.下列说法中,正确的是( )
A.在Rt△ABC中,锐角A的两边都扩大5倍,则cosA也扩大5倍
B.若45°<α<90°,则sinα>1
C.cos30°+cos45°=cos(30°+45°)
D.若α为锐角,tanα=,则sinα=
4.在Rt△ABC中,∠C=90°,sinA=,则cosB等于( )
A. B. C. D.
5.3tan60°的值为( )
A. B. C. D.3
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A. B. C. D.
8.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75?sin55° B.75?cos55° C.75?tan55° D.
9.如图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值等于( )
A. B. C. D.
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
二.填空题(共8小题)
11.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
12.如图所示的网格是正方形网格,∠BAC ∠DAE.(填“>”,“=”或“<”)
13.已知:tanx=2,则= .
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 .
15.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(﹣cosB)2=0,则∠C= °.
16.用科学记算器计算:2×sin15°×cos15°= .
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD= .
18.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1,参考数据:=1.41,=1.73 )
三.解答题(共8小题)
19.学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad60°的值为
A. B.1 C. D.2
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 .
(3)已知sinα=,其中α为锐角,试求sadα的值.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
22.计算:6tan230°﹣cos30°?tan60°﹣2sin45°+cos60°.
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
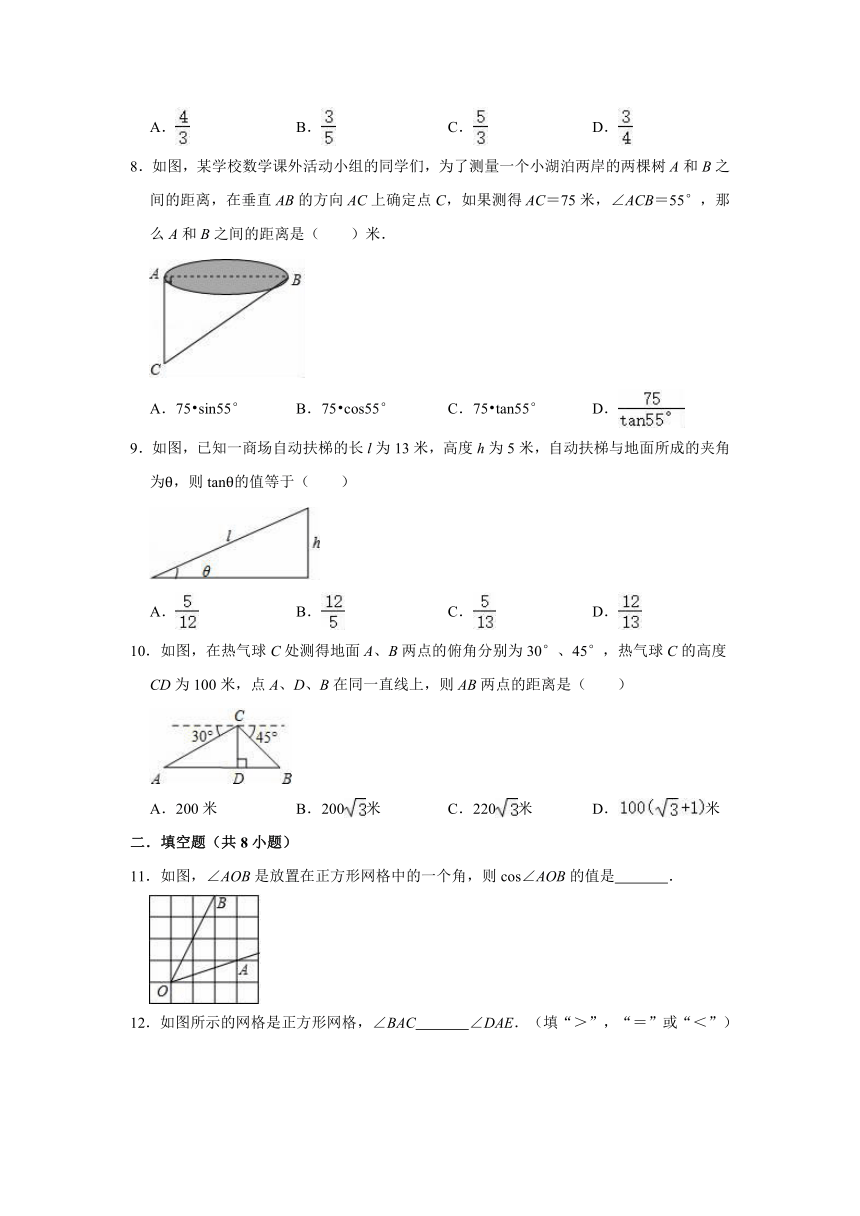
24.如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60米,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部支架HE的长为0.75米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1米;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
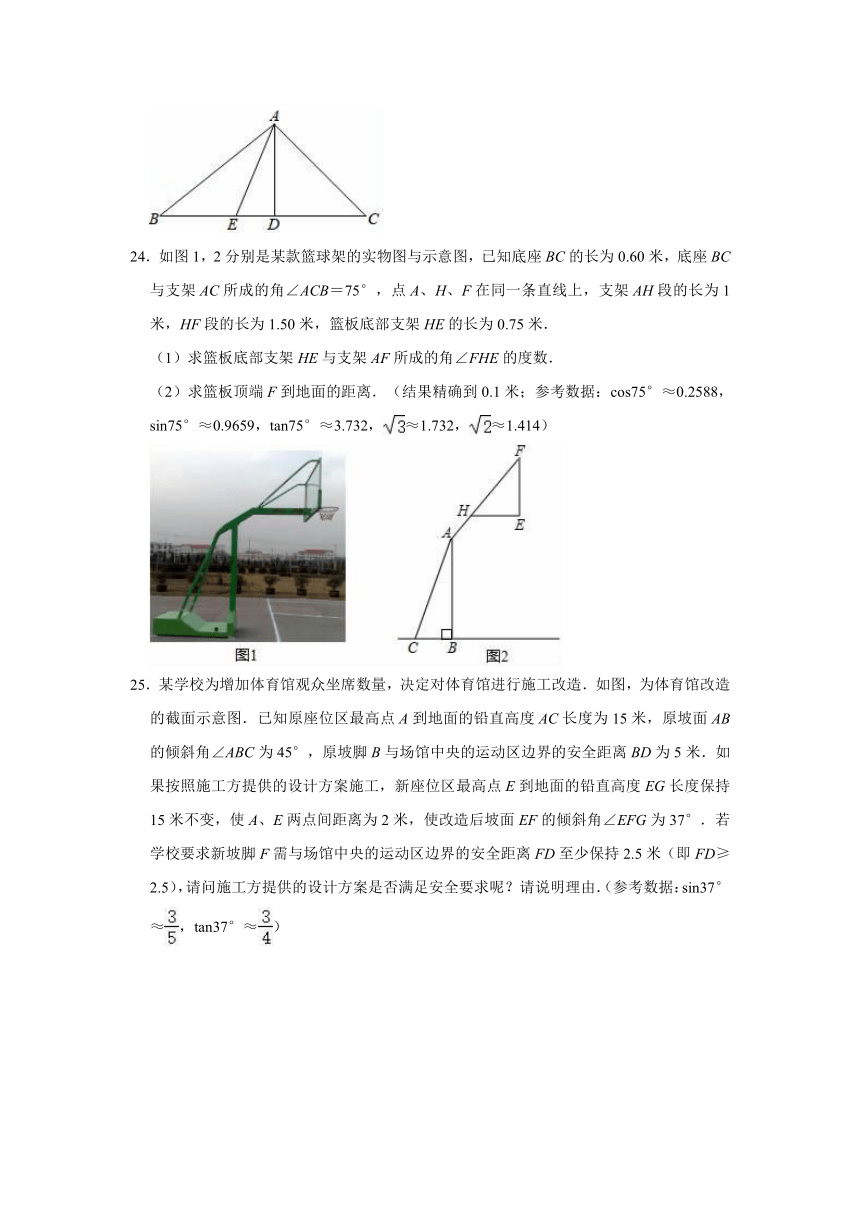
25.某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈,tan37°≈)
26.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈,tan63.4°≈2)
2019年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
【分析】根据勾股定理求出OA,根据正弦的定义解答即可.
【解答】解:由题意得,OC=2,AC=4,
由勾股定理得,AO==2,
∴sinA==,
故选:A.
【点评】本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
2.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
【分析】易得边长扩大后的三角形与原三角形相似,那么对应角相等,相应的三角函数值不变.
【解答】解:∵各边都扩大5倍,
∴新三角形与原三角形的对应边的比为5:1,
∴两三角形相似,
∴∠A的三角函数值不变,
故选:A.
【点评】用到的知识点为:三边对应成比例,两三角形相似;相似三角形的对应角相等.三角函数值只与角的大小有关,与角的边的长短无关.
3.下列说法中,正确的是( )
A.在Rt△ABC中,锐角A的两边都扩大5倍,则cosA也扩大5倍
B.若45°<α<90°,则sinα>1
C.cos30°+cos45°=cos(30°+45°)
D.若α为锐角,tanα=,则sinα=
【分析】根据三角函数的定义利用排除法求解.
【解答】解:A、在Rt△ABC中,锐角A的两边都扩大5倍,但它们的比值不变,所以cosA值不变,故本选项错误;
B、应为若45°<α<90°,则<sinα<1,故本选项错误;
C、三角函数的度数不能直接相加,故本选项错误;
D、根据tanα=设两直角边为5k、12k,根据勾股定理得斜边为13k,所以sinα=,故本选项正确.
故选:D.
【点评】本题利用三角函数的性质求解.
4.在Rt△ABC中,∠C=90°,sinA=,则cosB等于( )
A. B. C. D.
【分析】根据三角函数定义解答.
【解答】解:在Rt△ABC中,∠C=90°,sinA=,
设BC=3x,则AB=5x,
∴AC=4x.
∴cosB==.
故选:C.
【点评】本题可以考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
5.3tan60°的值为( )
A. B. C. D.3
【分析】把tan60的数值代入即可求解.
【解答】解:3tan60°=3×=3.
故选:D.
【点评】本题考查了特殊角的三角函数值,正确记忆特殊角的三角函数值是关键.
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
【分析】利用计算器求出数值,再计算即可.
【解答】解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
【点评】本题结合计算器的用法,旨在考查对基本概念的应用能力.
7.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A. B. C. D.
【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AD,再根据等边对等角的性质可得∠A=∠ACD,然后根据正切函数的定义列式求出∠A的正切值,即为tan∠ACD的值.
【解答】解:∵CD是AB边上的中线,
∴CD=AD,
∴∠A=∠ACD,
∵∠ACB=90°,BC=6,AC=8,
∴tan∠A=,
∴tan∠ACD的值.
故选:D.
【点评】本题考查了锐角三角函数的定义,直角三角形斜边上的中线等于斜边的一半的性质,等边对等角的性质,求出∠A=∠ACD是解本题的关键.
8.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75?sin55° B.75?cos55° C.75?tan55° D.
【分析】根据题意,可得Rt△ABC,同时可知AC与∠ACB.根据三角函数的定义解答.
【解答】解:根据题意,在Rt△ABC,有AC=75,∠ACB=55°,且tanα=,
则AB=AC×tan55°=75?tan55°,
故选:C.
【点评】本题考查了解直角三角形的应用,要熟练掌握三角函数的定义.
9.如图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值等于( )
A. B. C. D.
【分析】在由自动扶梯构成的直角三角形中,已知了坡面l和铅直高度h的长,可用勾股定理求出坡面的水平宽度,进而求出θ的正切值.
【解答】解:∵商场自动扶梯的长l=13米,高度h=5米,
∴m===12米,
∴tanθ=;
故选:A.
【点评】本题考查了解直角三角形的应用,用到的知识点是勾股定理,正确理解三角函数的定义求出m的长是关键.
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
【分析】在热气球C处测得地面B点的俯角分别为45°,BD=CD=100米,再在Rt△ACD中求出AD的长,据此即可求出AB的长.
【解答】解:∵在热气球C处测得地面B点的俯角分别为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角分别为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
【点评】本题考查了解直角三角形的应用﹣﹣仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
二.填空题(共8小题)
11.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
【分析】首先连接AB,由勾股定理易求得OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,然后由勾股定理的逆定理,可证得△AOB是等腰直角三角形,继而可求得cos∠AOB的值.
【解答】解:连接AB,
∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°=.
故答案为:.
【点评】此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
12.如图所示的网格是正方形网格,∠BAC > ∠DAE.(填“>”,“=”或“<”)
【分析】解法一:取点G、F,构建等腰直角三角形,由正切的值可作判断,或直接根据∠BAC=45°,∠EAD<∠FAG=45°,来作判断;
解法二:作辅助线,构建三角形及高线NP,先利用面积法求高线PN=,再分别求∠BAC、∠DAE的正弦,根据正弦值随着角度的增大而增大,作判断.
【解答】解:解法一:在AD上取一点G,在网格上取点F,构建△AFG为等腰直角三角形,
∵tan∠BAC==1,tan∠EAD<1,
∴∠BAC>∠EAD;
解法二:连接NH,BC,过N作NP⊥AD于P,
S△ANH=2×2﹣﹣×1×1=AH?NP,
=PN,
PN=,
Rt△ANP中,sin∠NAP====0.6,
Rt△ABC中,sin∠BAC===>0.6,
∵正弦值随着角度的增大而增大,
∴∠BAC>∠DAE,
故答案为:>.
【点评】本题考查了锐角三角函数的增减性,构建直角三角形求角的三角函数值进行判断,熟练掌握锐角三角函数的增减性是关键.
13.已知:tanx=2,则= .
【分析】分式中分子分母同时除以cosx,可得出关于tanx的分式,代入tanx的值即可得出答案.
【解答】解:分子分母同时除以cosx,原分式可化为:,
当tanx=2时,原式==.
故答案为:.
【点评】此题考查了同角三角函数的知识,解答本题的关键是掌握tanx=这一变换,有一定的技巧性.
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 .
【分析】根据所给的角的正弦值可得两条边的比,进而可得第三边长,tanB的值=∠B的对边与邻边之比.
【解答】解:∵在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
设a为3k,则c为5k,
根据勾股定理可得:b=4k,
∴tanB==,
故答案为:.
【点评】考查求锐角的三角函数值的方法通常为:利用锐角三角函数的定义,通过设参数的方法求三角函数值.
15.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(﹣cosB)2=0,则∠C= 75 °.
【分析】根据非负数的性质求出tanA和cosB的值,然后求出∠A、∠B的度数,最后求出∠C.
【解答】解:由题意得,tanA=1,cosB=,
则∠A=45°,∠B=60°,
则∠C=180°﹣45°﹣60°=75°.
故答案为:75.
【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
16.用科学记算器计算:2×sin15°×cos15°= 0.5 .
【分析】本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
【解答】解:用计算器按MODE,有DEG后,按2×sin15×cos15=显示结果为0.5.
故答案为0.5.
【点评】本题考查了熟练应用计算器的能力.
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD= .
【分析】延长AD和BC交于点E,在直角△ABE中利用三角函数求得BE的长,则EC的长即可求得,然后在直角△CDE中利用三角函数的定义求解.
【解答】解:延长AD和BC交于点E.
∵在直角△ABE中,tanA==,AB=3,
∴BE=4,
∴EC=BE﹣BC=4﹣2=2,
∵△ABE和△CDE中,∠B=∠EDC=90°,∠E=∠E,
∴∠DCE=∠A,
∴直角△CDE中,tan∠DCE=tanA==,
∴设DE=4x,则DC=3x,
在直角△CDE中,EC2=DE2+DC2,
∴4=16x2+9x2,
解得:x=,
则CD=.
故答案是:.
【点评】此题考查了相似三角形的判定与性质,含30度直角三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.
18.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 2.9 米(结果精确到0.1,参考数据:=1.41,=1.73 )
【分析】首先根据等腰直角三角形的性质可得DM=AM=4m,再根据勾股定理可得MC2+MB2=(2MC)2,代入数可得答案.
【解答】解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
【点评】此题主要考查了解直角三角形,勾股定理得应用,关键是掌握锐角三角函数的应用,属于中考常考题型.
三.解答题(共8小题)
19.学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad60°的值为
A. B.1 C. D.2
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 0<sadA<2 .
(3)已知sinα=,其中α为锐角,试求sadα的值.
【分析】(1)根据等腰三角形的性质,求出底角的度数,判断出三角形为等边三角形,再根据正对的定义解答;
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)作出直角△ABC,构造等腰三角形ACD,根据正对的定义解答.
【解答】解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°==1.
故选B.
(2)当∠A接近0°时,sadα接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadα接近2.
于是sadA的取值范围是0<sadA<2.
故答案为0<sadA<2.
(3)如图,在△ABC中,∠ACB=90°,sin∠A=.
在AB上取点D,使AD=AC,
作DH⊥AC,H为垂足,令BC=3k,AB=5k,
则AD=AC==4k,
又∵在△ADH中,∠AHD=90°,sin∠A=.
∴DH=ADsin∠A=k,AH==k.
则在△CDH中,CH=AC﹣AH=k,CD==k.
于是在△ACD中,AD=AC=4k,CD=k.
由正对的定义可得:sadA==,即sadα=.
【点评】此题是一道新定义的题目,考查了正对这一新内容,要熟悉三角函数的定义,可进行类比解答.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
【分析】(1)利用三角函数的定义和三角形的三边关系得到该结论不成立;
(2)举出反例进行论证.
【解答】解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
【点评】本题考查了同角三角函数的关系.解题的关键是掌握锐角三角函数的定义和特殊角的三角函数值.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【分析】(1)将α=30°代入,根据三角函数值计算可得;
(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【解答】解:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
【点评】本题主要考查特殊锐角的三角函数值及正弦函数的定义,熟练掌握三角函数的定义及勾股定理是解题的关键.
22.计算:6tan230°﹣cos30°?tan60°﹣2sin45°+cos60°.
【分析】根据特殊角的三角函数值计算.
【解答】解:原式=.
【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,题型以选择题、填空题为主.
【相关链接】特殊角三角函数值:
sin30°=,cos30°=,tan30°=,cot30°=;
sin45°=,cos45°=,tan45°=1,cot45°=1;
sin60°=,cos60°=,tan60°=,cot60°=.
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
【分析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=2,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE﹣CD,然后在Rt△ADE中根据正切函数的定义即可求解.
【解答】解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴AB==3,
∴BD==2,
∴BC=BD+DC=2+1;
(2)∵AE是BC边上的中线,
∴CE=BC=+,
∴DE=CE﹣CD=+﹣1=﹣,
∴tan∠DAE===﹣.
【点评】本题考查了解直角三角形,三角形的高、中线的定义,勾股定理,难度中等,分别解Rt△ADC与Rt△ADB,得出DC=1,AB=3是解题的关键.
24.如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60米,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部支架HE的长为0.75米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1米;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
【分析】(1)直接利用锐角三角函数关系得出cos∠FHE==,进而得出答案;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,解直角三角形即可得到结论.
【解答】解:(1)由题意可得:cos∠FHE==,
则∠FHE=60°;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,
在Rt△ABC中,tan∠ACB=,
∴AB=BC?tan75°=0.60×3.732=2.2392,
∴GM=AB=2.2392,
在Rt△AGF中,∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG≈2.17(m),
∴FM=FG+GM≈4.4(米),
答:篮板顶端F到地面的距离是4.4米.
【点评】本题考查解直角三角形、锐角三角函数、解题的关键是添加辅助线,构造直角三角形,记住锐角三角函数的定义,属于中考常考题型.
25.某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈,tan37°≈)
【分析】在Rt△ABC中通过解直角三角形可求出BC的长度,在Rt△EFG中通过解直角三角形可求出GF的长度,由EG=AC=15m、AC⊥BC、EG⊥BC可得出四边形EGCA是矩形,进而可得出GC的长度,再根据BF=GF﹣GC﹣BC、FD=BD﹣BF即可求出FD的长度,由FD的长度小于2.5米可得出施工方提供的设计方案不满足安全要求.
【解答】解:施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC==15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=≈=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴BF=GF﹣GC﹣BC≈20﹣15﹣2=3m.
∵BD=5m,
∴FD=BD﹣BF≈5﹣3=2<2.5,
∴施工方提供的设计方案不满足安全要求.
【点评】本题考查了解直角三角形的应用中的坡度坡角问题,通过解直角三角形求出BC、GF的长度是解题的关键.
26.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈,tan63.4°≈2)
【分析】(1)过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5米,然后根据勾股定理求得AG,即可求得斜坡AB的坡度i.
(2)在Rt△BCF中,BF==,在Rt△CEF中,EF==,得到方程BF﹣EF=﹣=4,解得CF=16,即可求得求DC=21.
【解答】解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)在Rt△BCF中,BF==,
在Rt△CEF中,EF==,
∵BE=4米,
∴BF﹣EF═﹣=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.
【点评】本题考查了解直角三角形的应用﹣仰角和俯角问题,解直角三角形的应用﹣坡度和坡比问题,正确理解题意是解题的关键.
一.选择题(共10小题)
1.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
2.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
3.下列说法中,正确的是( )
A.在Rt△ABC中,锐角A的两边都扩大5倍,则cosA也扩大5倍
B.若45°<α<90°,则sinα>1
C.cos30°+cos45°=cos(30°+45°)
D.若α为锐角,tanα=,则sinα=
4.在Rt△ABC中,∠C=90°,sinA=,则cosB等于( )
A. B. C. D.
5.3tan60°的值为( )
A. B. C. D.3
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A. B. C. D.
8.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75?sin55° B.75?cos55° C.75?tan55° D.
9.如图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值等于( )
A. B. C. D.
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
二.填空题(共8小题)
11.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
12.如图所示的网格是正方形网格,∠BAC ∠DAE.(填“>”,“=”或“<”)
13.已知:tanx=2,则= .
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 .
15.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(﹣cosB)2=0,则∠C= °.
16.用科学记算器计算:2×sin15°×cos15°= .
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD= .
18.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果精确到0.1,参考数据:=1.41,=1.73 )
三.解答题(共8小题)
19.学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad60°的值为
A. B.1 C. D.2
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 .
(3)已知sinα=,其中α为锐角,试求sadα的值.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
22.计算:6tan230°﹣cos30°?tan60°﹣2sin45°+cos60°.
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
24.如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60米,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部支架HE的长为0.75米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1米;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
25.某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈,tan37°≈)
26.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈,tan63.4°≈2)
2019年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
【分析】根据勾股定理求出OA,根据正弦的定义解答即可.
【解答】解:由题意得,OC=2,AC=4,
由勾股定理得,AO==2,
∴sinA==,
故选:A.
【点评】本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
2.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
【分析】易得边长扩大后的三角形与原三角形相似,那么对应角相等,相应的三角函数值不变.
【解答】解:∵各边都扩大5倍,
∴新三角形与原三角形的对应边的比为5:1,
∴两三角形相似,
∴∠A的三角函数值不变,
故选:A.
【点评】用到的知识点为:三边对应成比例,两三角形相似;相似三角形的对应角相等.三角函数值只与角的大小有关,与角的边的长短无关.
3.下列说法中,正确的是( )
A.在Rt△ABC中,锐角A的两边都扩大5倍,则cosA也扩大5倍
B.若45°<α<90°,则sinα>1
C.cos30°+cos45°=cos(30°+45°)
D.若α为锐角,tanα=,则sinα=
【分析】根据三角函数的定义利用排除法求解.
【解答】解:A、在Rt△ABC中,锐角A的两边都扩大5倍,但它们的比值不变,所以cosA值不变,故本选项错误;
B、应为若45°<α<90°,则<sinα<1,故本选项错误;
C、三角函数的度数不能直接相加,故本选项错误;
D、根据tanα=设两直角边为5k、12k,根据勾股定理得斜边为13k,所以sinα=,故本选项正确.
故选:D.
【点评】本题利用三角函数的性质求解.
4.在Rt△ABC中,∠C=90°,sinA=,则cosB等于( )
A. B. C. D.
【分析】根据三角函数定义解答.
【解答】解:在Rt△ABC中,∠C=90°,sinA=,
设BC=3x,则AB=5x,
∴AC=4x.
∴cosB==.
故选:C.
【点评】本题可以考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
5.3tan60°的值为( )
A. B. C. D.3
【分析】把tan60的数值代入即可求解.
【解答】解:3tan60°=3×=3.
故选:D.
【点评】本题考查了特殊角的三角函数值,正确记忆特殊角的三角函数值是关键.
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
【分析】利用计算器求出数值,再计算即可.
【解答】解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
【点评】本题结合计算器的用法,旨在考查对基本概念的应用能力.
7.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A. B. C. D.
【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AD,再根据等边对等角的性质可得∠A=∠ACD,然后根据正切函数的定义列式求出∠A的正切值,即为tan∠ACD的值.
【解答】解:∵CD是AB边上的中线,
∴CD=AD,
∴∠A=∠ACD,
∵∠ACB=90°,BC=6,AC=8,
∴tan∠A=,
∴tan∠ACD的值.
故选:D.
【点评】本题考查了锐角三角函数的定义,直角三角形斜边上的中线等于斜边的一半的性质,等边对等角的性质,求出∠A=∠ACD是解本题的关键.
8.如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
A.75?sin55° B.75?cos55° C.75?tan55° D.
【分析】根据题意,可得Rt△ABC,同时可知AC与∠ACB.根据三角函数的定义解答.
【解答】解:根据题意,在Rt△ABC,有AC=75,∠ACB=55°,且tanα=,
则AB=AC×tan55°=75?tan55°,
故选:C.
【点评】本题考查了解直角三角形的应用,要熟练掌握三角函数的定义.
9.如图,已知一商场自动扶梯的长l为13米,高度h为5米,自动扶梯与地面所成的夹角为θ,则tanθ的值等于( )
A. B. C. D.
【分析】在由自动扶梯构成的直角三角形中,已知了坡面l和铅直高度h的长,可用勾股定理求出坡面的水平宽度,进而求出θ的正切值.
【解答】解:∵商场自动扶梯的长l=13米,高度h=5米,
∴m===12米,
∴tanθ=;
故选:A.
【点评】本题考查了解直角三角形的应用,用到的知识点是勾股定理,正确理解三角函数的定义求出m的长是关键.
10.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
【分析】在热气球C处测得地面B点的俯角分别为45°,BD=CD=100米,再在Rt△ACD中求出AD的长,据此即可求出AB的长.
【解答】解:∵在热气球C处测得地面B点的俯角分别为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角分别为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
【点评】本题考查了解直角三角形的应用﹣﹣仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
二.填空题(共8小题)
11.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是 .
【分析】首先连接AB,由勾股定理易求得OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,然后由勾股定理的逆定理,可证得△AOB是等腰直角三角形,继而可求得cos∠AOB的值.
【解答】解:连接AB,
∵OA2=12+32=10,AB2=12+32=10,OB2=22+42=20,
∴OA2+AB2=OB2,OA=AB,
∴△AOB是等腰直角三角形,即∠OAB=90°,
∴∠AOB=45°,
∴cos∠AOB=cos45°=.
故答案为:.
【点评】此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
12.如图所示的网格是正方形网格,∠BAC > ∠DAE.(填“>”,“=”或“<”)
【分析】解法一:取点G、F,构建等腰直角三角形,由正切的值可作判断,或直接根据∠BAC=45°,∠EAD<∠FAG=45°,来作判断;
解法二:作辅助线,构建三角形及高线NP,先利用面积法求高线PN=,再分别求∠BAC、∠DAE的正弦,根据正弦值随着角度的增大而增大,作判断.
【解答】解:解法一:在AD上取一点G,在网格上取点F,构建△AFG为等腰直角三角形,
∵tan∠BAC==1,tan∠EAD<1,
∴∠BAC>∠EAD;
解法二:连接NH,BC,过N作NP⊥AD于P,
S△ANH=2×2﹣﹣×1×1=AH?NP,
=PN,
PN=,
Rt△ANP中,sin∠NAP====0.6,
Rt△ABC中,sin∠BAC===>0.6,
∵正弦值随着角度的增大而增大,
∴∠BAC>∠DAE,
故答案为:>.
【点评】本题考查了锐角三角函数的增减性,构建直角三角形求角的三角函数值进行判断,熟练掌握锐角三角函数的增减性是关键.
13.已知:tanx=2,则= .
【分析】分式中分子分母同时除以cosx,可得出关于tanx的分式,代入tanx的值即可得出答案.
【解答】解:分子分母同时除以cosx,原分式可化为:,
当tanx=2时,原式==.
故答案为:.
【点评】此题考查了同角三角函数的知识,解答本题的关键是掌握tanx=这一变换,有一定的技巧性.
14.已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 .
【分析】根据所给的角的正弦值可得两条边的比,进而可得第三边长,tanB的值=∠B的对边与邻边之比.
【解答】解:∵在Rt△ABC中,∠C=90°,sinA=,
∴sinA==,
设a为3k,则c为5k,
根据勾股定理可得:b=4k,
∴tanB==,
故答案为:.
【点评】考查求锐角的三角函数值的方法通常为:利用锐角三角函数的定义,通过设参数的方法求三角函数值.
15.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(﹣cosB)2=0,则∠C= 75 °.
【分析】根据非负数的性质求出tanA和cosB的值,然后求出∠A、∠B的度数,最后求出∠C.
【解答】解:由题意得,tanA=1,cosB=,
则∠A=45°,∠B=60°,
则∠C=180°﹣45°﹣60°=75°.
故答案为:75.
【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
16.用科学记算器计算:2×sin15°×cos15°= 0.5 .
【分析】本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
【解答】解:用计算器按MODE,有DEG后,按2×sin15×cos15=显示结果为0.5.
故答案为0.5.
【点评】本题考查了熟练应用计算器的能力.
17.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD= .
【分析】延长AD和BC交于点E,在直角△ABE中利用三角函数求得BE的长,则EC的长即可求得,然后在直角△CDE中利用三角函数的定义求解.
【解答】解:延长AD和BC交于点E.
∵在直角△ABE中,tanA==,AB=3,
∴BE=4,
∴EC=BE﹣BC=4﹣2=2,
∵△ABE和△CDE中,∠B=∠EDC=90°,∠E=∠E,
∴∠DCE=∠A,
∴直角△CDE中,tan∠DCE=tanA==,
∴设DE=4x,则DC=3x,
在直角△CDE中,EC2=DE2+DC2,
∴4=16x2+9x2,
解得:x=,
则CD=.
故答案是:.
【点评】此题考查了相似三角形的判定与性质,含30度直角三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.
18.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 2.9 米(结果精确到0.1,参考数据:=1.41,=1.73 )
【分析】首先根据等腰直角三角形的性质可得DM=AM=4m,再根据勾股定理可得MC2+MB2=(2MC)2,代入数可得答案.
【解答】解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
【点评】此题主要考查了解直角三角形,勾股定理得应用,关键是掌握锐角三角函数的应用,属于中考常考题型.
三.解答题(共8小题)
19.学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad60°的值为
A. B.1 C. D.2
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 0<sadA<2 .
(3)已知sinα=,其中α为锐角,试求sadα的值.
【分析】(1)根据等腰三角形的性质,求出底角的度数,判断出三角形为等边三角形,再根据正对的定义解答;
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)作出直角△ABC,构造等腰三角形ACD,根据正对的定义解答.
【解答】解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°==1.
故选B.
(2)当∠A接近0°时,sadα接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadα接近2.
于是sadA的取值范围是0<sadA<2.
故答案为0<sadA<2.
(3)如图,在△ABC中,∠ACB=90°,sin∠A=.
在AB上取点D,使AD=AC,
作DH⊥AC,H为垂足,令BC=3k,AB=5k,
则AD=AC==4k,
又∵在△ADH中,∠AHD=90°,sin∠A=.
∴DH=ADsin∠A=k,AH==k.
则在△CDH中,CH=AC﹣AH=k,CD==k.
于是在△ACD中,AD=AC=4k,CD=k.
由正对的定义可得:sadA==,即sadα=.
【点评】此题是一道新定义的题目,考查了正对这一新内容,要熟悉三角函数的定义,可进行类比解答.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
【分析】(1)利用三角函数的定义和三角形的三边关系得到该结论不成立;
(2)举出反例进行论证.
【解答】解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
【点评】本题考查了同角三角函数的关系.解题的关键是掌握锐角三角函数的定义和特殊角的三角函数值.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【分析】(1)将α=30°代入,根据三角函数值计算可得;
(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【解答】解:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
【点评】本题主要考查特殊锐角的三角函数值及正弦函数的定义,熟练掌握三角函数的定义及勾股定理是解题的关键.
22.计算:6tan230°﹣cos30°?tan60°﹣2sin45°+cos60°.
【分析】根据特殊角的三角函数值计算.
【解答】解:原式=.
【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,题型以选择题、填空题为主.
【相关链接】特殊角三角函数值:
sin30°=,cos30°=,tan30°=,cot30°=;
sin45°=,cos45°=,tan45°=1,cot45°=1;
sin60°=,cos60°=,tan60°=,cot60°=.
23.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
【分析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=2,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE﹣CD,然后在Rt△ADE中根据正切函数的定义即可求解.
【解答】解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴AB==3,
∴BD==2,
∴BC=BD+DC=2+1;
(2)∵AE是BC边上的中线,
∴CE=BC=+,
∴DE=CE﹣CD=+﹣1=﹣,
∴tan∠DAE===﹣.
【点评】本题考查了解直角三角形,三角形的高、中线的定义,勾股定理,难度中等,分别解Rt△ADC与Rt△ADB,得出DC=1,AB=3是解题的关键.
24.如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60米,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部支架HE的长为0.75米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1米;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
【分析】(1)直接利用锐角三角函数关系得出cos∠FHE==,进而得出答案;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,解直角三角形即可得到结论.
【解答】解:(1)由题意可得:cos∠FHE==,
则∠FHE=60°;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,
在Rt△ABC中,tan∠ACB=,
∴AB=BC?tan75°=0.60×3.732=2.2392,
∴GM=AB=2.2392,
在Rt△AGF中,∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG≈2.17(m),
∴FM=FG+GM≈4.4(米),
答:篮板顶端F到地面的距离是4.4米.
【点评】本题考查解直角三角形、锐角三角函数、解题的关键是添加辅助线,构造直角三角形,记住锐角三角函数的定义,属于中考常考题型.
25.某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈,tan37°≈)
【分析】在Rt△ABC中通过解直角三角形可求出BC的长度,在Rt△EFG中通过解直角三角形可求出GF的长度,由EG=AC=15m、AC⊥BC、EG⊥BC可得出四边形EGCA是矩形,进而可得出GC的长度,再根据BF=GF﹣GC﹣BC、FD=BD﹣BF即可求出FD的长度,由FD的长度小于2.5米可得出施工方提供的设计方案不满足安全要求.
【解答】解:施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC==15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=≈=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴BF=GF﹣GC﹣BC≈20﹣15﹣2=3m.
∵BD=5m,
∴FD=BD﹣BF≈5﹣3=2<2.5,
∴施工方提供的设计方案不满足安全要求.
【点评】本题考查了解直角三角形的应用中的坡度坡角问题,通过解直角三角形求出BC、GF的长度是解题的关键.
26.重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.
(参考数据:tan53°≈,tan63.4°≈2)
【分析】(1)过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5米,然后根据勾股定理求得AG,即可求得斜坡AB的坡度i.
(2)在Rt△BCF中,BF==,在Rt△CEF中,EF==,得到方程BF﹣EF=﹣=4,解得CF=16,即可求得求DC=21.
【解答】解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5米,
∵AB=13米,
∴AG==12米,
∴AB的坡度i==1:2.4;
(2)在Rt△BCF中,BF==,
在Rt△CEF中,EF==,
∵BE=4米,
∴BF﹣EF═﹣=4,
解得:CF=16.
∴DC=CF+DF=16+5=21米.
【点评】本题考查了解直角三角形的应用﹣仰角和俯角问题,解直角三角形的应用﹣坡度和坡比问题,正确理解题意是解题的关键.
