新人教版九年级下册数学第26章反比例函数知识点+例题练习学案(pdf版、不含答案)
文档属性
| 名称 | 新人教版九年级下册数学第26章反比例函数知识点+例题练习学案(pdf版、不含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 461.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 20:41:47 | ||
图片预览


文档简介
1
反比例函数
一、反比例函数概念
一般地,如果两个变量 x、y 之间的关系可以表示成
x
ky ? 或 kxy=b 或 y=kx-1 (k为常数, 0k ? )的形式,那么称
y 是 x的反比例函数。
注意点:
(1)k 是常数,且 k 不为零;
(2)
x
k
中分母 x 的指数为 1,如, 2
2y
x
? 就不是反比例函数。
(3)自变量 x 的取值范围是 0x ? 的一切实数.
(4)自变量 y 的取值范围是 0y ? 的一切实数。
练习一、
1.如果函数
2 2( 1) my m x ?? ? 为反比例函数,则m的值是
2.函数
2 2 9( 2) m my m x ? ?? ? 是反比例函数,则m的值是
二、反比例解析式
用待定系数法求反比例函数关系式的一般步骤是:
①设所求的反比例函数为:
x
ky ? ( 0k ? );
②根据已知条件,列出含 k 的方程;
③解出待定系数 k 的值;
④把 k值代入函数关系式
x
ky ? 中。
练习二、已知 y -2 与 x成反比例,当 x =3 时, y =1,则 y与 x间的函数关系式为 学.科
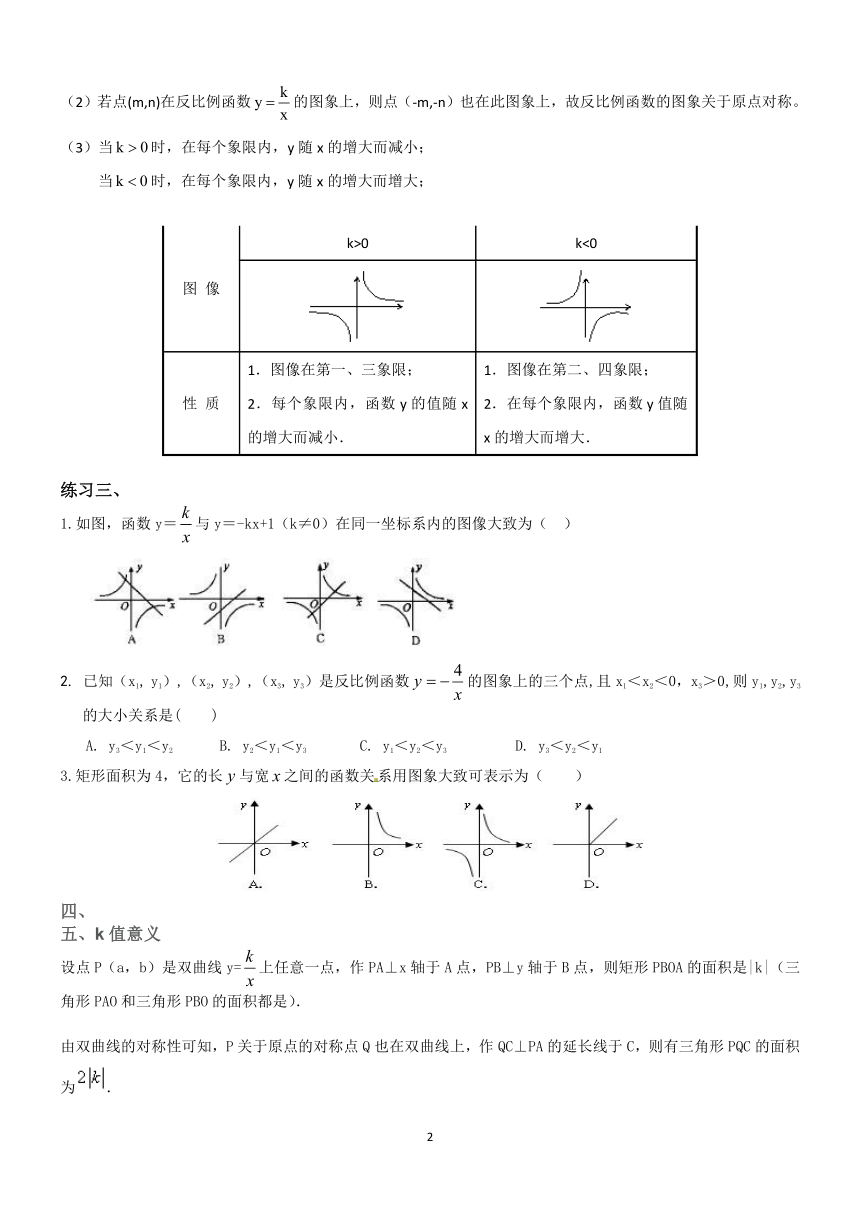
三、反比例图像及性质:
x
ky ? )0k( ?
(1)其图象的位置是:
当 0k ? 时,x、y 同号,图象在第一、三象限;
当 0k ? 时,x、y 异号,图象在第二、四象限。
图象的形状:双曲线.
越大,图象的弯曲度越小,曲线越平直. 越小,图象的弯曲度越大.
2
(2)若点(m,n)在反比例函数
x
ky ? 的图象上,则点(-m,-n)也在此图象上,故反比例函数的图象关于原点对称。
(3)当 0k ? 时,在每个象限内,y 随 x的增大而减小;
当 0k ? 时,在每个象限内,y 随 x 的增大而增大;
图 像
k>0 k<0
性 质
1.图像在第一、三象限;
2.每个象限内,函数 y 的值随 x
的增大而减小.
1.图像在第二、四象限;
2.在每个象限内,函数 y 值随
x的增大而增大.
练习三、
1.如图,函数 y=
k
x
与 y=-kx+1(k≠0)在同一坐标系内的图像大致为( )
2. 已知(x1, y1),(x2, y2),(x3, y3)是反比例函数 x
y 4?? 的图象上的三个点,且 x1<x2<0,x3>0,则 y1,y2,y3
的大小关系是( )
A. y3<y1<y2 B. y2<y1<y3 C. y1<y2<y3 D. y3<y2<y1
3.矩形面积为 4,它的长 y与宽 x之间的函数关系用图象大致可表示为( )
四、
五、k 值意义
设点 P(a,b)是双曲线 y=
x
k
上任意一点,作 PA⊥x 轴于 A点,PB⊥y轴于 B 点,则矩形 PBOA 的面积是|k|(三
角形 PAO 和三角形 PBO 的面积都是).
由双曲线的对称性可知,P 关于原点的对称点 Q 也在双曲线上,作 QC⊥PA 的延长线于 C,则有三角形 PQC 的面积
为 .
3
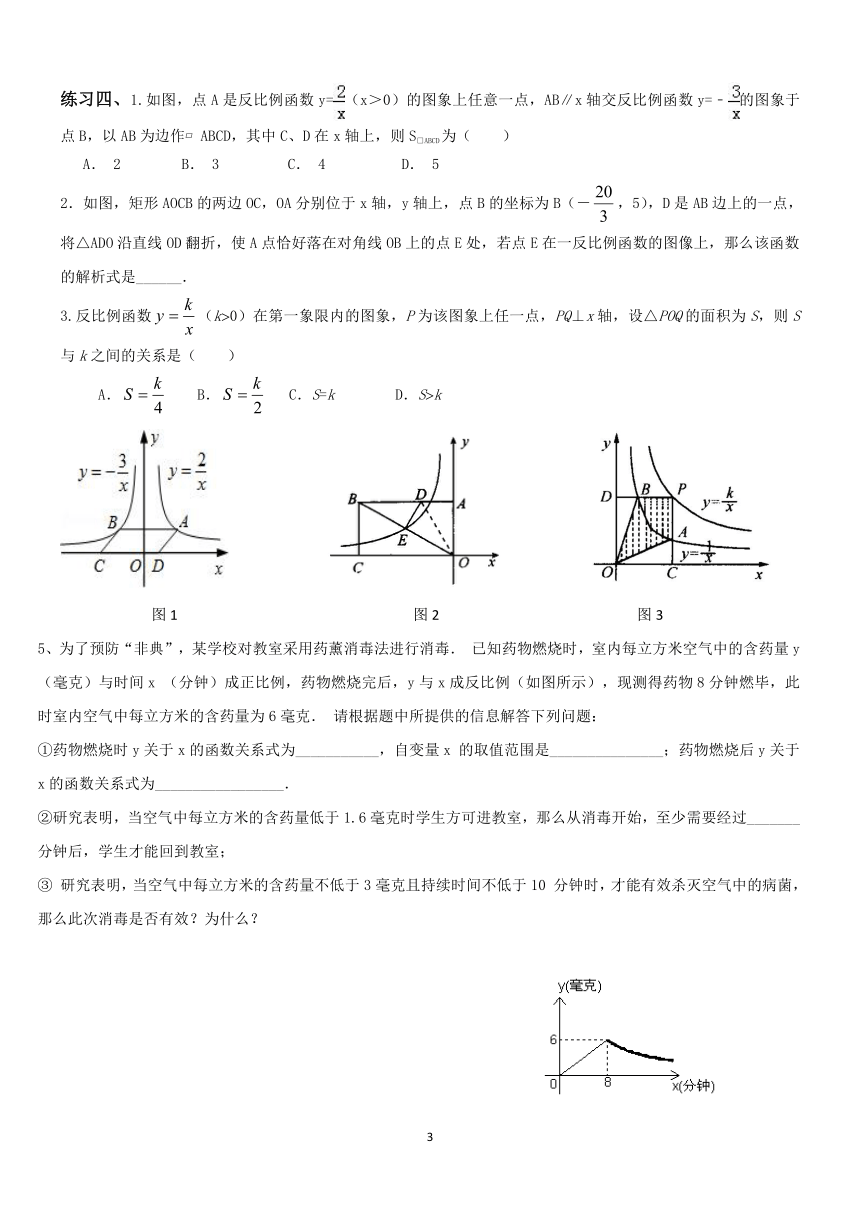
练习四、1.如图,点 A 是反比例函数 y= (x>0)的图象上任意一点,AB∥x 轴交反比例函数 y=﹣ 的图象于
点 B,以 AB 为边作? ABCD,其中 C、D在 x轴上,则 S□ABCD为( )
A. 2 B. 3 C. 4 D. 5
2.如图,矩形 AOCB 的两边 OC,OA 分别位于 x 轴,y轴上,点 B 的坐标为 B(-
3
20
,5),D是 AB 边上的一点,
将△ADO 沿直线 OD 翻折,使 A点恰好落在对角线 OB 上的点 E处,若点 E在一反比例函数的图像上,那么该函数
的解析式是______.
3.反比例函数
x
ky ? (k?0)在第一象限内的图象,P 为该图象上任一点,PQ⊥x 轴,设△POQ 的面积为 S,则 S
与 k 之间的关系是( )
A.
4
kS ? B.
2
kS ? C.S=k D.S?k
图 1 图 2 图 3
5、为了预防“非典”,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量 y
(毫克)与时间 x (分钟)成正比例,药物燃烧完后,y 与 x 成反比例(如图所示),现测得药物 8 分钟燃毕,此
时室内空气中每立方米的含药量为 6 毫克. 请根据题中所提供的信息解答下列问题:
①药物燃烧时 y关于 x 的函数关系式为___________,自变量 x 的取值范围是_______________;药物燃烧后 y 关于
x的函数关系式为_________________.
②研究表明,当空气中每立方米的含药量低于 1.6 毫克时学生方可进教室,那么从消毒开始,至少需要经过_______
分钟后,学生才能回到教室;
③ 研究表明,当空气中每立方米的含药量不低于 3 毫克且持续时间不低于 10 分钟时,才能有效杀灭空气中的病菌,
那么此次消毒是否有效?为什么?
4
反比例存在性问题
类型一:反比例函数中等腰三角形找点问题
1、如图,已知反比例函数
x
ky ? (k<0)的图象经过点 A(— 3,m)点 A 作 AB⊥x轴于点 B,且△AOB 的面
积为 3 .(1)求 k 和 m 的值;(2)若一次函数 y=ax+1 的图象经过点 A,并且与 x 轴相交于点 C,求|AO|:|AC|
的值;(3)若 D 为坐标轴上一点,使△AOD是以 AO 为一腰的等腰三角形,请写出所有满足条件的 D点的坐标.
2、 已知:如图,一次函数 y=-2x 的图象与反比例函数 y=
x
k
的图象交于 A、B 两点,且点 B 的坐标为(1,m).
(1)求反比例函数 y=
x
k
的表达式;
(2)点 C(n,1)在反比例函数 y=
x
k
的图象上,求△AOC 的面积;
(3)在(2)的条件下,在坐标轴上找出一点 P,使△APC 为等腰三角形,请直接写出所有符合条件的点 P 的坐
标.
5
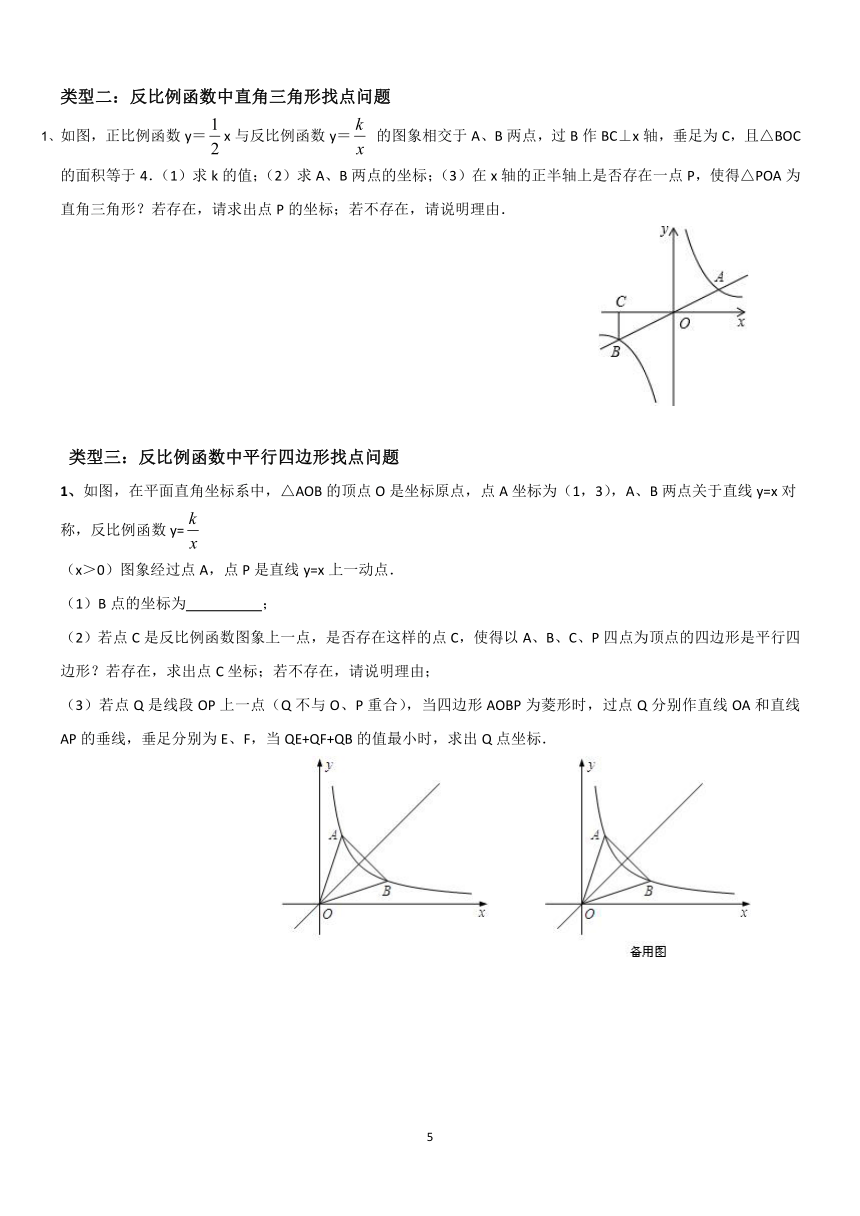
类型二:反比例函数中直角三角形找点问题
1、如图,正比例函数 y=
2
1
x 与反比例函数 y=
x
k
的图象相交于 A、B 两点,过 B 作 BC⊥x 轴,垂足为 C,且△BOC
的面积等于 4.(1)求 k 的值;(2)求 A、B 两点的坐标;(3)在 x轴的正半轴上是否存在一点 P,使得△POA 为
直角三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由.
类型三:反比例函数中平行四边形找点问题
1、如图,在平面直角坐标系中,△AOB 的顶点 O 是坐标原点,点 A 坐标为(1,3),A、B 两点关于直线 y=x 对
称,反比例函数 y=
x
k
(x>0)图象经过点 A,点 P 是直线 y=x 上一动点.
(1)B 点的坐标为 ;
(2)若点 C 是反比例函数图象上一点,是否存在这样的点 C,使得以 A、B、C、P 四点为顶点的四边形是平行四
边形?若存在,求出点 C 坐标;若不存在,请说明理由;
(3)若点 Q 是线段 OP 上一点(Q 不与 O、P 重合),当四边形 AOBP 为菱形时,过点 Q 分别作直线 OA 和直线
AP 的垂线,垂足分别为 E、F,当 QE+QF+QB 的值最小时,求出 Q 点坐标.
6
2、如图,把一块等腰直角三角板 ABC 放在平面直角坐标系的第二象限内,若∠A=90°,AB=AC,且 A、B 两点的
坐标分别为(-4,0)、(0,2).(1)求点 C 的坐标;(2)将△ABC 沿 x 轴的正方向平移 m 个单位长度至第一象限
内的△DEF 位置,若 B、C 两点的对应点 E、F 都在反比例函数 y=
x
k
的图象上,求 m、k的值和直线 EF 的解析式;
(3)在(2)的条件下,直线 EF 交 y 轴于点 G,问是否存在 x轴上的点 M 和反比例函数图象上的点 P,使得四
边形 PGMF 是平行四边形?若存在,求出点 M 和点 P 的坐标;若不存在,请说明理由.
2、如图,四边形 OABC 为矩形,以点 O 为原点建立直角坐标系,点 C 在 x轴的正半轴上,点 A 在 y 轴的正半轴
上,已知点 B 为(2,4),反比例函数 y=
x
m
图象经过 AB 的中点 D,且与 BC 交于点 E.(1)求 m 的值和点 E 的
坐标;(2)求直线 DE 的解析式;(3)点 Q 为 x轴上一点,点 P 为反比例函数 y=
x
m
图象上一点,是否存在点 P、
Q,使得以 P、Q、D、E 为顶点的四边形为平行四边形?如果存在,请求出点 P 的坐标;如果不存在,请说明理
由.
7
3、已知一次函数 y1=ax+b 的图象与反比例函数 y2=
x
k
的图象相交于 A、B 两点,坐标分别为(-2,4)、(4,-2).(1)
求两个函数的解析式;(2)结合图象写出 y1<y2 时,x的取值范围;(3)求△AOB 的面积;
(4)是否存在一点 P,使以点 A﹑B﹑O﹑P 为顶点的四边形为菱形?若存在,求出顶点 P 的坐标;若不存在,请
说明理由.
4、 如图,一次函数 y=kx+b 的图象与反比例函数 y=
x
m
(x>0)的图象交于点 P(n,2),与 x 轴交于点 A(-4,
0),与 y 轴交于点 C,PB⊥x 轴于点 B,且 AC=BC.(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点 D,使四边形 BCPD 为菱形?如果存在,求出点 D 的坐标;如果不存在,说明
理由.
8
5、 已知,如图,菱形 ABCD 的一边 BC 在 x轴上,且 C 点坐标为(-1,0),D 点坐标(0, 3).反比例函数 y=
x
k
过菱形的顶点 A.(1)求反比例函数的解析式;(2)若 P 为反比例函数在第四象限的图象上一点,点 Q 在 x 轴上,
问是否存在点 P、Q,使得四边形 CDQP 为矩形?若存在,求出 P 和 Q 的坐标;若不存在,说明理由.
类型四:反比例函数中图形等面积问题
例 1、如图,一次函数 y=ax+b 的图象与反比例函数 y=
x
k
的图象交于 C,D 两点,与坐标轴交于 A、B 两点,连
接 OC,OD(O 是坐标原点).①利用图中条件,求反比例函数的解析式和 m 的值;②当 x>0 时,双曲线上是
否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明并求出点 P 的坐标;若不存在,说明理由.
9
2、如图,已知正比例函数和反比例函数的图象都经过点 M(-2,-1),且 P(-1,-2)为双曲线上的一点,Q为坐
标平面上一动点,PA垂直于 x 轴,QB 垂直于 y 轴,垂足分别是 A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点 Q 在直线 MO 上运动时,直线 MO 上是否存在这样的点 Q,使得△OBQ 与△OAP 面积相等?如果存在,
请求出点的坐标;如果不存在,请说明理由.
类型五:反比例函数中图形 面积倍分问题
1、如图,M 点是正比例函数 y=kx 和反比例函数 y=
x
m
的图象的一个交点.(1)求这两个函数的解析式;(2)
在反比例函数 y=
x
m
的图象上取一点 P,过点 P 做 PA垂直于 x 轴,垂足为 A,点 Q 是直线 MO 上一点,QB 垂直
于 y 轴,垂足为 B,直线 MO 上是否存在这样的点 Q,使得△OBQ 的面积是△OPA的面积的 2 倍?如果存在,请
求出点 Q 的坐标;如果不存在,请说明理由.
10
2、如图,在平面直角坐标系中,直线 AB 与 x轴交于点 B,与 y 轴交于点 A,与反比例函数 y=x
m
的图象在
第二象限交于点 C,CE⊥x 轴,垂足为点 E,tan∠ABO=
1
2
,OB=4,OE=2.
(1) 求反比例函数的解析式;
(2) 若点 D 是反比例函数图象在第四象限上的点,过点 D作 DF⊥y轴,垂足为点 F,连接 OD、BF,如果 S△BAF=4S△DFO,
求点 D 的坐标.
类型六:反比例函数中相似三角形存在性问题
1、如图,一次函数 y=ax+b 的图象与反比例函数 y=
x
k
的图象交于 A,B 两点,与 x 轴交于点 C,与 y 轴交于点 D,
已知 OA= 10 ,tan∠AOC=
3
1
,点 B 的坐标为(m,-2).(1)求反比例函数的解析式;
(2)求一次函数的解析式;(3)在 y 轴上存在一点 P,使得△PDC 与△ODC 相似,请你求出 P 点的坐标.
11
反比例函数综合
1.如图,直线 AB经过第一象限,分别与 x轴、y轴交于 A、B两点,P为线段 AB上任意一点(不与 A、B重合),
过点 P分别向 x轴、y轴作垂线,垂足分别为 C、D.设 OC=x,四边形 OCPD的面积为 S.
(1)若已知 A(4,0),B(0,6),求 S与 x之间的函数关系式;
(2)若已知 A(a,0),B(0,b),且当 x= 3
4
时,S有最大值 9
8
,求 a、b的值;
(3)在(2)的条件下,在直线 AB上有一点 M,且点 M到 x轴、y轴的距离相等,点 N在过 M点的反比例函
数图象上,且△OAN是直角三角形,求点 N的坐标.
2.如图,直角梯形 OABC的腰 OC在 y轴的正半轴上,点 A(5n,0)在 x轴的负半轴上,OA :AB :OC=5 : 5 : 3.点
D是线段 OC上一点,且 OD=BD.
(1)若直线 y=kx+m(k≠0)过 B、D两点,求 k的值;
(2)在(1)的条件下,反比例函数 y= m
x
的图象经过点 B.
①求证:反比例函数 y= m
x
的图象与直线 AB必有两个不同的交点;
②设反比例函数 y= m
x
的图象与直线 AB的另一个交点为 E,已知点 P(p,-n-1),Q(q,-n-2)在
线段 AB上,当点 E落在线段 PQ上时,求 n的取值范围.
12
3.已知点 P(m,n)是反比例函数 y= 6
x
(x>0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数 y
=
3
x
(x>0)的图象于点 A、B,点 C是直线 y=2x上的一点.
(1)请用含 m的代数式分别表示 P、A、B三点的坐标;
(2)在点 P运动过程中,连接 AB,△PAB的面积是否变化,若不变,请求出△PAB的面积;若改变,说明理由;
(3)在点 P运动过程中,以点 P、A、B、C为顶点的四边形能否为平行四边形,若能,请求出此时 m的值;若
不能,请说明理由.
4.如图,已知一次函数 y1=kx+b的图象与 x轴相交于点 A,与反比例函数 y2= c
x
的图象相交于 B(-1,5)、
C( 5
2
,d)两点.点 P(m,n)是一次函数 y1=kx+b的图象上的动点.
(1)求 k、b的值;
(2)设-1<m < 3
2
,过点 P作 x轴的平行线与函数 y2= c
x
的图象相交于点 D.试问△PAD的面积是否存在
最大值?若存在,请求出面积的最大值及此时点 P的坐标;若不存在,请说明理由;
(3)设 m=1-a,如果在两个实数 m与 n之间(不包括 m和 n)有且只有一个整数,求实数 a的取值范围.
13
5.如图,双曲线 y= 3
16x
(x>0)与过 A(1,0)、B(0,1)的直线交于 P、Q两点,连接 OP、OQ.点 C是
线段 OA上一点(不与 O、A重合),CD⊥AB于 D,DE⊥OB于 E.设 CA=a.
(1)求证:△OAQ≌△OBP;
(2)当 a为何值时,CE=AC?
(3)是否存在这样的点 C,使得△OEF为等腰三角形?若存在,求出此时点 C的坐标;若不存在,请说明理由.
6.如图,已知双曲线 y= k
x
经过点 D(6,1),点 C是双曲线第三象限分支上的动点,过 C作 CA⊥x轴,过 D
作 DB⊥y轴,垂足分别为 A,B,连接 AB,BC.
(1)求 k的值;
(2)若△BCD的面积为 12,求直线 CD的解析式;
(3)判断 AB与 CD的位置关系,并说明理由.
14
7.如图,正方形 AOCB的边长为 4,反比例函数的图象过点 E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段 BC交于点 D,直线 y=- 1
2
x+b过点 D,与线段 AB相交于点 F,求 F的坐标;
(3)连接 OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
(4)若点 P是 x轴上的动点,点 Q是(1)中的反比例在第一象限图象上的动点,且使得△PDQ为等腰直角三
角形,直接写出点 P的坐标.
8.如图,反比例函数 y= k
x
的图象经过点 A(a,b)且| a+2 3|+( b-2 3)2=0,直线 y=2x-2与 x轴交于点
B,与 y轴交于点 C.
(1)求反比例函数的解析式;
(2)将线段 BC绕坐标平面内的某点 M旋转 180° 后 B、C两点恰好都落在反比例函数的图象上,求点 M的坐标;
(3)在反比例函数的图象上是否存在点 P,使以 PB为直径的圆恰好过点 C?若存在,求点 P的坐标,若不存在,
请说明理由.
15
9.如图,在平面直角坐标系 xOy中,梯形 AOBC的边 OB在 x轴的正半轴上,AC∥OB,BC⊥OB,过点 A的双
曲线 y= k
x
的一支在第一象限交梯形对角线 OC于点 D,交边 BC于点 E.
(1)填空:双曲线的另一支在第_________象限,k的取值范围是_______________;
(2)若点 C的坐标为(2,2),当点 E在什么位置时,阴影部分面积 S最小?
(3)若 OD
OC
=
1
2
,S△OAC =2,求双曲线的解析式.
10.已知点 A(1,c)和点 B(3,d)是直线 y=k1x+b与双曲线 y= k2
x
(k2>0)的交点.
(1)过点 A作 AM⊥x轴,垂足为 M,连接 BM.若 AM=BM,求点 B的坐标;
(2)设点 P在线段 AB上,过点 P作 PE⊥x轴,垂足为 E,并交双曲线 y= k2
x
(k2>0)于点 N.当 PN
NE
取最
大值时,有 PN= 1
2
,求此时双曲线的解析式.
16
11.已知点 A是双曲线 y= k1
x
(k1>0)上一点,点 A的横坐标为 1,过点 A作平行于 y轴的直线,与 x轴交于
点 B,与双曲线 y= k2
x
(k2<0)交于点 C.点 D(m,0)是 x轴上一点,且位于直线 AC右侧,E是 AD的中点.
(1)如图 1,当 m=4时,求△ACD的面积(用含 k1、k2的代数式表示);
(2)如图 2,若点 E恰好在双曲线 y= k1
x
(k1>0)上,求 m的值;
(3)如图 3,设线段 EB的延长线与 y轴的负半轴交于点 F,当 m=2时,若△BDF的面积为 1,且 CF∥AD,
求 k1的值,并直接写出线段 CF的长.
反比例函数
一、反比例函数概念
一般地,如果两个变量 x、y 之间的关系可以表示成
x
ky ? 或 kxy=b 或 y=kx-1 (k为常数, 0k ? )的形式,那么称
y 是 x的反比例函数。
注意点:
(1)k 是常数,且 k 不为零;
(2)
x
k
中分母 x 的指数为 1,如, 2
2y
x
? 就不是反比例函数。
(3)自变量 x 的取值范围是 0x ? 的一切实数.
(4)自变量 y 的取值范围是 0y ? 的一切实数。
练习一、
1.如果函数
2 2( 1) my m x ?? ? 为反比例函数,则m的值是
2.函数
2 2 9( 2) m my m x ? ?? ? 是反比例函数,则m的值是
二、反比例解析式
用待定系数法求反比例函数关系式的一般步骤是:
①设所求的反比例函数为:
x
ky ? ( 0k ? );
②根据已知条件,列出含 k 的方程;
③解出待定系数 k 的值;
④把 k值代入函数关系式
x
ky ? 中。
练习二、已知 y -2 与 x成反比例,当 x =3 时, y =1,则 y与 x间的函数关系式为 学.科
三、反比例图像及性质:
x
ky ? )0k( ?
(1)其图象的位置是:
当 0k ? 时,x、y 同号,图象在第一、三象限;
当 0k ? 时,x、y 异号,图象在第二、四象限。
图象的形状:双曲线.
越大,图象的弯曲度越小,曲线越平直. 越小,图象的弯曲度越大.
2
(2)若点(m,n)在反比例函数
x
ky ? 的图象上,则点(-m,-n)也在此图象上,故反比例函数的图象关于原点对称。
(3)当 0k ? 时,在每个象限内,y 随 x的增大而减小;
当 0k ? 时,在每个象限内,y 随 x 的增大而增大;
图 像
k>0 k<0
性 质
1.图像在第一、三象限;
2.每个象限内,函数 y 的值随 x
的增大而减小.
1.图像在第二、四象限;
2.在每个象限内,函数 y 值随
x的增大而增大.
练习三、
1.如图,函数 y=
k
x
与 y=-kx+1(k≠0)在同一坐标系内的图像大致为( )
2. 已知(x1, y1),(x2, y2),(x3, y3)是反比例函数 x
y 4?? 的图象上的三个点,且 x1<x2<0,x3>0,则 y1,y2,y3
的大小关系是( )
A. y3<y1<y2 B. y2<y1<y3 C. y1<y2<y3 D. y3<y2<y1
3.矩形面积为 4,它的长 y与宽 x之间的函数关系用图象大致可表示为( )
四、
五、k 值意义
设点 P(a,b)是双曲线 y=
x
k
上任意一点,作 PA⊥x 轴于 A点,PB⊥y轴于 B 点,则矩形 PBOA 的面积是|k|(三
角形 PAO 和三角形 PBO 的面积都是).
由双曲线的对称性可知,P 关于原点的对称点 Q 也在双曲线上,作 QC⊥PA 的延长线于 C,则有三角形 PQC 的面积
为 .
3
练习四、1.如图,点 A 是反比例函数 y= (x>0)的图象上任意一点,AB∥x 轴交反比例函数 y=﹣ 的图象于
点 B,以 AB 为边作? ABCD,其中 C、D在 x轴上,则 S□ABCD为( )
A. 2 B. 3 C. 4 D. 5
2.如图,矩形 AOCB 的两边 OC,OA 分别位于 x 轴,y轴上,点 B 的坐标为 B(-
3
20
,5),D是 AB 边上的一点,
将△ADO 沿直线 OD 翻折,使 A点恰好落在对角线 OB 上的点 E处,若点 E在一反比例函数的图像上,那么该函数
的解析式是______.
3.反比例函数
x
ky ? (k?0)在第一象限内的图象,P 为该图象上任一点,PQ⊥x 轴,设△POQ 的面积为 S,则 S
与 k 之间的关系是( )
A.
4
kS ? B.
2
kS ? C.S=k D.S?k
图 1 图 2 图 3
5、为了预防“非典”,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量 y
(毫克)与时间 x (分钟)成正比例,药物燃烧完后,y 与 x 成反比例(如图所示),现测得药物 8 分钟燃毕,此
时室内空气中每立方米的含药量为 6 毫克. 请根据题中所提供的信息解答下列问题:
①药物燃烧时 y关于 x 的函数关系式为___________,自变量 x 的取值范围是_______________;药物燃烧后 y 关于
x的函数关系式为_________________.
②研究表明,当空气中每立方米的含药量低于 1.6 毫克时学生方可进教室,那么从消毒开始,至少需要经过_______
分钟后,学生才能回到教室;
③ 研究表明,当空气中每立方米的含药量不低于 3 毫克且持续时间不低于 10 分钟时,才能有效杀灭空气中的病菌,
那么此次消毒是否有效?为什么?
4
反比例存在性问题
类型一:反比例函数中等腰三角形找点问题
1、如图,已知反比例函数
x
ky ? (k<0)的图象经过点 A(— 3,m)点 A 作 AB⊥x轴于点 B,且△AOB 的面
积为 3 .(1)求 k 和 m 的值;(2)若一次函数 y=ax+1 的图象经过点 A,并且与 x 轴相交于点 C,求|AO|:|AC|
的值;(3)若 D 为坐标轴上一点,使△AOD是以 AO 为一腰的等腰三角形,请写出所有满足条件的 D点的坐标.
2、 已知:如图,一次函数 y=-2x 的图象与反比例函数 y=
x
k
的图象交于 A、B 两点,且点 B 的坐标为(1,m).
(1)求反比例函数 y=
x
k
的表达式;
(2)点 C(n,1)在反比例函数 y=
x
k
的图象上,求△AOC 的面积;
(3)在(2)的条件下,在坐标轴上找出一点 P,使△APC 为等腰三角形,请直接写出所有符合条件的点 P 的坐
标.
5
类型二:反比例函数中直角三角形找点问题
1、如图,正比例函数 y=
2
1
x 与反比例函数 y=
x
k
的图象相交于 A、B 两点,过 B 作 BC⊥x 轴,垂足为 C,且△BOC
的面积等于 4.(1)求 k 的值;(2)求 A、B 两点的坐标;(3)在 x轴的正半轴上是否存在一点 P,使得△POA 为
直角三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由.
类型三:反比例函数中平行四边形找点问题
1、如图,在平面直角坐标系中,△AOB 的顶点 O 是坐标原点,点 A 坐标为(1,3),A、B 两点关于直线 y=x 对
称,反比例函数 y=
x
k
(x>0)图象经过点 A,点 P 是直线 y=x 上一动点.
(1)B 点的坐标为 ;
(2)若点 C 是反比例函数图象上一点,是否存在这样的点 C,使得以 A、B、C、P 四点为顶点的四边形是平行四
边形?若存在,求出点 C 坐标;若不存在,请说明理由;
(3)若点 Q 是线段 OP 上一点(Q 不与 O、P 重合),当四边形 AOBP 为菱形时,过点 Q 分别作直线 OA 和直线
AP 的垂线,垂足分别为 E、F,当 QE+QF+QB 的值最小时,求出 Q 点坐标.
6
2、如图,把一块等腰直角三角板 ABC 放在平面直角坐标系的第二象限内,若∠A=90°,AB=AC,且 A、B 两点的
坐标分别为(-4,0)、(0,2).(1)求点 C 的坐标;(2)将△ABC 沿 x 轴的正方向平移 m 个单位长度至第一象限
内的△DEF 位置,若 B、C 两点的对应点 E、F 都在反比例函数 y=
x
k
的图象上,求 m、k的值和直线 EF 的解析式;
(3)在(2)的条件下,直线 EF 交 y 轴于点 G,问是否存在 x轴上的点 M 和反比例函数图象上的点 P,使得四
边形 PGMF 是平行四边形?若存在,求出点 M 和点 P 的坐标;若不存在,请说明理由.
2、如图,四边形 OABC 为矩形,以点 O 为原点建立直角坐标系,点 C 在 x轴的正半轴上,点 A 在 y 轴的正半轴
上,已知点 B 为(2,4),反比例函数 y=
x
m
图象经过 AB 的中点 D,且与 BC 交于点 E.(1)求 m 的值和点 E 的
坐标;(2)求直线 DE 的解析式;(3)点 Q 为 x轴上一点,点 P 为反比例函数 y=
x
m
图象上一点,是否存在点 P、
Q,使得以 P、Q、D、E 为顶点的四边形为平行四边形?如果存在,请求出点 P 的坐标;如果不存在,请说明理
由.
7
3、已知一次函数 y1=ax+b 的图象与反比例函数 y2=
x
k
的图象相交于 A、B 两点,坐标分别为(-2,4)、(4,-2).(1)
求两个函数的解析式;(2)结合图象写出 y1<y2 时,x的取值范围;(3)求△AOB 的面积;
(4)是否存在一点 P,使以点 A﹑B﹑O﹑P 为顶点的四边形为菱形?若存在,求出顶点 P 的坐标;若不存在,请
说明理由.
4、 如图,一次函数 y=kx+b 的图象与反比例函数 y=
x
m
(x>0)的图象交于点 P(n,2),与 x 轴交于点 A(-4,
0),与 y 轴交于点 C,PB⊥x 轴于点 B,且 AC=BC.(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点 D,使四边形 BCPD 为菱形?如果存在,求出点 D 的坐标;如果不存在,说明
理由.
8
5、 已知,如图,菱形 ABCD 的一边 BC 在 x轴上,且 C 点坐标为(-1,0),D 点坐标(0, 3).反比例函数 y=
x
k
过菱形的顶点 A.(1)求反比例函数的解析式;(2)若 P 为反比例函数在第四象限的图象上一点,点 Q 在 x 轴上,
问是否存在点 P、Q,使得四边形 CDQP 为矩形?若存在,求出 P 和 Q 的坐标;若不存在,说明理由.
类型四:反比例函数中图形等面积问题
例 1、如图,一次函数 y=ax+b 的图象与反比例函数 y=
x
k
的图象交于 C,D 两点,与坐标轴交于 A、B 两点,连
接 OC,OD(O 是坐标原点).①利用图中条件,求反比例函数的解析式和 m 的值;②当 x>0 时,双曲线上是
否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明并求出点 P 的坐标;若不存在,说明理由.
9
2、如图,已知正比例函数和反比例函数的图象都经过点 M(-2,-1),且 P(-1,-2)为双曲线上的一点,Q为坐
标平面上一动点,PA垂直于 x 轴,QB 垂直于 y 轴,垂足分别是 A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点 Q 在直线 MO 上运动时,直线 MO 上是否存在这样的点 Q,使得△OBQ 与△OAP 面积相等?如果存在,
请求出点的坐标;如果不存在,请说明理由.
类型五:反比例函数中图形 面积倍分问题
1、如图,M 点是正比例函数 y=kx 和反比例函数 y=
x
m
的图象的一个交点.(1)求这两个函数的解析式;(2)
在反比例函数 y=
x
m
的图象上取一点 P,过点 P 做 PA垂直于 x 轴,垂足为 A,点 Q 是直线 MO 上一点,QB 垂直
于 y 轴,垂足为 B,直线 MO 上是否存在这样的点 Q,使得△OBQ 的面积是△OPA的面积的 2 倍?如果存在,请
求出点 Q 的坐标;如果不存在,请说明理由.
10
2、如图,在平面直角坐标系中,直线 AB 与 x轴交于点 B,与 y 轴交于点 A,与反比例函数 y=x
m
的图象在
第二象限交于点 C,CE⊥x 轴,垂足为点 E,tan∠ABO=
1
2
,OB=4,OE=2.
(1) 求反比例函数的解析式;
(2) 若点 D 是反比例函数图象在第四象限上的点,过点 D作 DF⊥y轴,垂足为点 F,连接 OD、BF,如果 S△BAF=4S△DFO,
求点 D 的坐标.
类型六:反比例函数中相似三角形存在性问题
1、如图,一次函数 y=ax+b 的图象与反比例函数 y=
x
k
的图象交于 A,B 两点,与 x 轴交于点 C,与 y 轴交于点 D,
已知 OA= 10 ,tan∠AOC=
3
1
,点 B 的坐标为(m,-2).(1)求反比例函数的解析式;
(2)求一次函数的解析式;(3)在 y 轴上存在一点 P,使得△PDC 与△ODC 相似,请你求出 P 点的坐标.
11
反比例函数综合
1.如图,直线 AB经过第一象限,分别与 x轴、y轴交于 A、B两点,P为线段 AB上任意一点(不与 A、B重合),
过点 P分别向 x轴、y轴作垂线,垂足分别为 C、D.设 OC=x,四边形 OCPD的面积为 S.
(1)若已知 A(4,0),B(0,6),求 S与 x之间的函数关系式;
(2)若已知 A(a,0),B(0,b),且当 x= 3
4
时,S有最大值 9
8
,求 a、b的值;
(3)在(2)的条件下,在直线 AB上有一点 M,且点 M到 x轴、y轴的距离相等,点 N在过 M点的反比例函
数图象上,且△OAN是直角三角形,求点 N的坐标.
2.如图,直角梯形 OABC的腰 OC在 y轴的正半轴上,点 A(5n,0)在 x轴的负半轴上,OA :AB :OC=5 : 5 : 3.点
D是线段 OC上一点,且 OD=BD.
(1)若直线 y=kx+m(k≠0)过 B、D两点,求 k的值;
(2)在(1)的条件下,反比例函数 y= m
x
的图象经过点 B.
①求证:反比例函数 y= m
x
的图象与直线 AB必有两个不同的交点;
②设反比例函数 y= m
x
的图象与直线 AB的另一个交点为 E,已知点 P(p,-n-1),Q(q,-n-2)在
线段 AB上,当点 E落在线段 PQ上时,求 n的取值范围.
12
3.已知点 P(m,n)是反比例函数 y= 6
x
(x>0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数 y
=
3
x
(x>0)的图象于点 A、B,点 C是直线 y=2x上的一点.
(1)请用含 m的代数式分别表示 P、A、B三点的坐标;
(2)在点 P运动过程中,连接 AB,△PAB的面积是否变化,若不变,请求出△PAB的面积;若改变,说明理由;
(3)在点 P运动过程中,以点 P、A、B、C为顶点的四边形能否为平行四边形,若能,请求出此时 m的值;若
不能,请说明理由.
4.如图,已知一次函数 y1=kx+b的图象与 x轴相交于点 A,与反比例函数 y2= c
x
的图象相交于 B(-1,5)、
C( 5
2
,d)两点.点 P(m,n)是一次函数 y1=kx+b的图象上的动点.
(1)求 k、b的值;
(2)设-1<m < 3
2
,过点 P作 x轴的平行线与函数 y2= c
x
的图象相交于点 D.试问△PAD的面积是否存在
最大值?若存在,请求出面积的最大值及此时点 P的坐标;若不存在,请说明理由;
(3)设 m=1-a,如果在两个实数 m与 n之间(不包括 m和 n)有且只有一个整数,求实数 a的取值范围.
13
5.如图,双曲线 y= 3
16x
(x>0)与过 A(1,0)、B(0,1)的直线交于 P、Q两点,连接 OP、OQ.点 C是
线段 OA上一点(不与 O、A重合),CD⊥AB于 D,DE⊥OB于 E.设 CA=a.
(1)求证:△OAQ≌△OBP;
(2)当 a为何值时,CE=AC?
(3)是否存在这样的点 C,使得△OEF为等腰三角形?若存在,求出此时点 C的坐标;若不存在,请说明理由.
6.如图,已知双曲线 y= k
x
经过点 D(6,1),点 C是双曲线第三象限分支上的动点,过 C作 CA⊥x轴,过 D
作 DB⊥y轴,垂足分别为 A,B,连接 AB,BC.
(1)求 k的值;
(2)若△BCD的面积为 12,求直线 CD的解析式;
(3)判断 AB与 CD的位置关系,并说明理由.
14
7.如图,正方形 AOCB的边长为 4,反比例函数的图象过点 E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段 BC交于点 D,直线 y=- 1
2
x+b过点 D,与线段 AB相交于点 F,求 F的坐标;
(3)连接 OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
(4)若点 P是 x轴上的动点,点 Q是(1)中的反比例在第一象限图象上的动点,且使得△PDQ为等腰直角三
角形,直接写出点 P的坐标.
8.如图,反比例函数 y= k
x
的图象经过点 A(a,b)且| a+2 3|+( b-2 3)2=0,直线 y=2x-2与 x轴交于点
B,与 y轴交于点 C.
(1)求反比例函数的解析式;
(2)将线段 BC绕坐标平面内的某点 M旋转 180° 后 B、C两点恰好都落在反比例函数的图象上,求点 M的坐标;
(3)在反比例函数的图象上是否存在点 P,使以 PB为直径的圆恰好过点 C?若存在,求点 P的坐标,若不存在,
请说明理由.
15
9.如图,在平面直角坐标系 xOy中,梯形 AOBC的边 OB在 x轴的正半轴上,AC∥OB,BC⊥OB,过点 A的双
曲线 y= k
x
的一支在第一象限交梯形对角线 OC于点 D,交边 BC于点 E.
(1)填空:双曲线的另一支在第_________象限,k的取值范围是_______________;
(2)若点 C的坐标为(2,2),当点 E在什么位置时,阴影部分面积 S最小?
(3)若 OD
OC
=
1
2
,S△OAC =2,求双曲线的解析式.
10.已知点 A(1,c)和点 B(3,d)是直线 y=k1x+b与双曲线 y= k2
x
(k2>0)的交点.
(1)过点 A作 AM⊥x轴,垂足为 M,连接 BM.若 AM=BM,求点 B的坐标;
(2)设点 P在线段 AB上,过点 P作 PE⊥x轴,垂足为 E,并交双曲线 y= k2
x
(k2>0)于点 N.当 PN
NE
取最
大值时,有 PN= 1
2
,求此时双曲线的解析式.
16
11.已知点 A是双曲线 y= k1
x
(k1>0)上一点,点 A的横坐标为 1,过点 A作平行于 y轴的直线,与 x轴交于
点 B,与双曲线 y= k2
x
(k2<0)交于点 C.点 D(m,0)是 x轴上一点,且位于直线 AC右侧,E是 AD的中点.
(1)如图 1,当 m=4时,求△ACD的面积(用含 k1、k2的代数式表示);
(2)如图 2,若点 E恰好在双曲线 y= k1
x
(k1>0)上,求 m的值;
(3)如图 3,设线段 EB的延长线与 y轴的负半轴交于点 F,当 m=2时,若△BDF的面积为 1,且 CF∥AD,
求 k1的值,并直接写出线段 CF的长.
