北师大版八年级数学上册第五章二元一次方程组复习题课件(共33张PPT)
文档属性
| 名称 | 北师大版八年级数学上册第五章二元一次方程组复习题课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
第五章 二元一次方程组
兴宁市大坪中学 练小盛
八年级数学(上)
回顾与思考
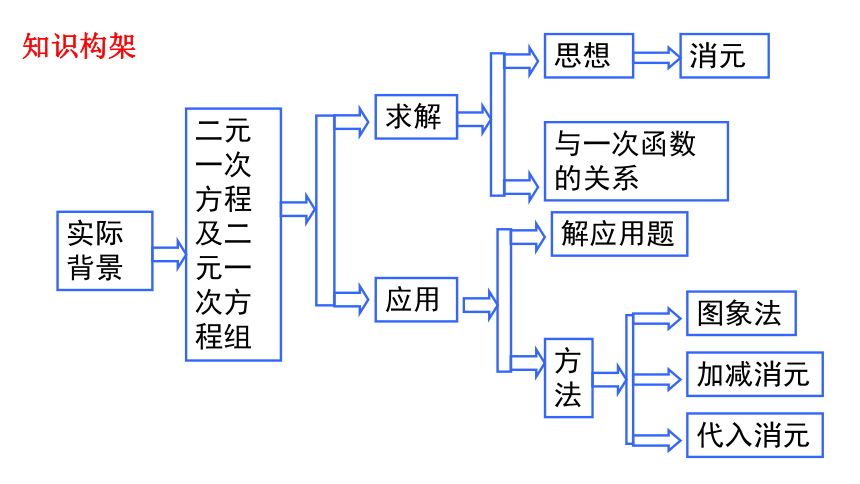
实际背景
二元一次方程及二元一次方程组
求解
应用
方法
思想
与一次函数的关系
消元
解应用题
图象法
加减消元
代入消元
知识构架
有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且所含未知数的项的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.
5.方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
(1).求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
(2).把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
(3).解一元一次方程,求出x的值;
(4).再把求出的x的值 代入变形后的方程,求
出y的值.
用加减法解二元一次方程组的步骤:
(1).利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
(2).把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
(3).解这个一元一次方程,求得一个未知数的值 ;
(4).把所求的这个未知的值代入方程组中较为简
便的一个方程,求出另一个未知数,从而得到方
程的解 .
①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③找出交点坐标,交点坐标即为方程组的解。
图象法解方程组的步骤:
6.列二元一次方程解决实际问题的一般步骤:
审:
设:
列:
解:
答:
审清题目中的等量关系.
设未知数.
根据等量关系,列出方程组.
解方程组,求出未知数.
检验所求出未知数是否符合题意,写出答案.
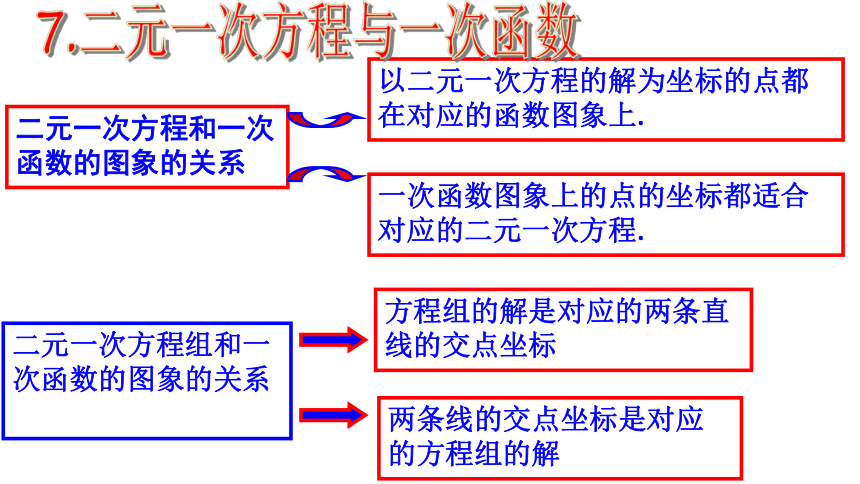
二元一次方程组和一次函数的图象的关系
方程组的解是对应的两条直线的交点坐标
两条线的交点坐标是对应的方程组的解
二元一次方程和一次函数的图象的关系
以二元一次方程的解为坐标的点都在对应的函数图象上.
一次函数图象上的点的坐标都适合对应的二元一次方程.
7.二元一次方程与一次函数
每个二元一次方程组都对应两个一次函数,两个一次函数图象的交点坐标就是相应的二元一次方程组的解。
二元一次方程组的解与对应的两个一次函数图象的关系:
(1)二元一次方程组无解→两个一次函数图象平行(无交点)
(2)二元一次方程组有一个解→两个一次函数图象相交(有一个交点即交点在y轴或非y轴)
(3)二元一次方程组有无数个解→两个一次函数图象重合(有无数个交点)
特别的:两平行直线的k相等;方程组中两方程未知数的系数对应成比例方程组无解,对应的两直线平行。
1.行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
4.销售问题:
标价×折扣=售价
售价-进价=利润
利润率=
复习题
C
(1)
解: ①
把代入①,得
所以原方程组的解是
(2)
解: ①
把代入②,得
所以原方程组的解是
(3)
解: ①
把代入①,得
所以原方程组的解是
(4)
解: ②11
把代入①,得
所以原方程组的解是
(5)
解:把①代入②,得
即④
把①代入③,得()3
把代入④,得
把,代入①,得
所以原方程组的解是
解:把和代入方程,得
解得
答:的值为5,b的值为2.
解:(1)由题意得 解得
(2)由(1)可得代数式为11
把上式,得
110
答:这个代数式的值是60.
解:设,
,依题意,得
解得
所以关系式为和
解:设, ,依题意,得
2
解得
所以关系式为和
联立方程组,得
解得
所以点A的坐标为A()
例如
解:设长方形的长为宽为,依题意,得
解得
答:该长方形的长为15cm,宽为7cm。
解:设长方形的长为宽为,
依题意,得
解得
答:该长方形的长为45cm,宽为15cm。
解:∵CE∥AD
∴∠A=∠BEC
∵BE=CE
∴∠B=∠BCE
∵∠B+∠BCE+∠BEC=180
∴∠A+2∠B=180
∵∠B-∠A=30
∴∠A=40,∠B=70
解:设甲组每天生产个产品,乙组每天生产个产品,依题意,得
解得
答:甲组每天生产个产品,乙组每天生产个产品
解:设船在静水中的速度为km/h,水流速度为km/h,依题意,得
解得
答:船在静水中的速度为km/h,水流速度为km/h.
解:设该专业户去年计划生产水稻t,小麦t,依题意,得
解得
答:该专业户去年实际生产水稻t,小麦t
(1+15)(吨) (1+10)(吨)
解:设投中个两分球,个罚球,依题意,得
解得
答:投中4个两分球,8个罚球.
解:设该商品进价为元,定价为元,依题意,得
解得
答:该商品进价为元,定价为元.
解:设甲商品进价为元,乙商品进价为 元,依题意,得
解得
答:甲商品进价为元,乙商品进价为 元.
解:设甲带钱,乙带钱,依题意,得
解得
答:甲带钱37.5,乙带钱25.
解:设(1)班有名学生,(2)班有名学生,依题意,得
解得
答: (1)班有名学生,(2)班有名学生;
联合起来购票能省302元。
49102
解:设①⑤两个正方形的边长分别为和,
依题意,得
解得
答:这个正方形的面积为143.
①
②
③
④
⑤
所以
解:方程组有无数个解,方程组所对应的两个一次函数的图象
(两条直线)重合。感悟到由两个函数图象互相重合的方程组
成的方程组有无数个解。
第五章 二元一次方程组
兴宁市大坪中学 练小盛
八年级数学(上)
回顾与思考
实际背景
二元一次方程及二元一次方程组
求解
应用
方法
思想
与一次函数的关系
消元
解应用题
图象法
加减消元
代入消元
知识构架
有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且所含未知数的项的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.
5.方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
(1).求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
(2).把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
(3).解一元一次方程,求出x的值;
(4).再把求出的x的值 代入变形后的方程,求
出y的值.
用加减法解二元一次方程组的步骤:
(1).利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
(2).把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
(3).解这个一元一次方程,求得一个未知数的值 ;
(4).把所求的这个未知的值代入方程组中较为简
便的一个方程,求出另一个未知数,从而得到方
程的解 .
①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③找出交点坐标,交点坐标即为方程组的解。
图象法解方程组的步骤:
6.列二元一次方程解决实际问题的一般步骤:
审:
设:
列:
解:
答:
审清题目中的等量关系.
设未知数.
根据等量关系,列出方程组.
解方程组,求出未知数.
检验所求出未知数是否符合题意,写出答案.
二元一次方程组和一次函数的图象的关系
方程组的解是对应的两条直线的交点坐标
两条线的交点坐标是对应的方程组的解
二元一次方程和一次函数的图象的关系
以二元一次方程的解为坐标的点都在对应的函数图象上.
一次函数图象上的点的坐标都适合对应的二元一次方程.
7.二元一次方程与一次函数
每个二元一次方程组都对应两个一次函数,两个一次函数图象的交点坐标就是相应的二元一次方程组的解。
二元一次方程组的解与对应的两个一次函数图象的关系:
(1)二元一次方程组无解→两个一次函数图象平行(无交点)
(2)二元一次方程组有一个解→两个一次函数图象相交(有一个交点即交点在y轴或非y轴)
(3)二元一次方程组有无数个解→两个一次函数图象重合(有无数个交点)
特别的:两平行直线的k相等;方程组中两方程未知数的系数对应成比例方程组无解,对应的两直线平行。
1.行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
4.销售问题:
标价×折扣=售价
售价-进价=利润
利润率=
复习题
C
(1)
解: ①
把代入①,得
所以原方程组的解是
(2)
解: ①
把代入②,得
所以原方程组的解是
(3)
解: ①
把代入①,得
所以原方程组的解是
(4)
解: ②11
把代入①,得
所以原方程组的解是
(5)
解:把①代入②,得
即④
把①代入③,得()3
把代入④,得
把,代入①,得
所以原方程组的解是
解:把和代入方程,得
解得
答:的值为5,b的值为2.
解:(1)由题意得 解得
(2)由(1)可得代数式为11
把上式,得
110
答:这个代数式的值是60.
解:设,
,依题意,得
解得
所以关系式为和
解:设, ,依题意,得
2
解得
所以关系式为和
联立方程组,得
解得
所以点A的坐标为A()
例如
解:设长方形的长为宽为,依题意,得
解得
答:该长方形的长为15cm,宽为7cm。
解:设长方形的长为宽为,
依题意,得
解得
答:该长方形的长为45cm,宽为15cm。
解:∵CE∥AD
∴∠A=∠BEC
∵BE=CE
∴∠B=∠BCE
∵∠B+∠BCE+∠BEC=180
∴∠A+2∠B=180
∵∠B-∠A=30
∴∠A=40,∠B=70
解:设甲组每天生产个产品,乙组每天生产个产品,依题意,得
解得
答:甲组每天生产个产品,乙组每天生产个产品
解:设船在静水中的速度为km/h,水流速度为km/h,依题意,得
解得
答:船在静水中的速度为km/h,水流速度为km/h.
解:设该专业户去年计划生产水稻t,小麦t,依题意,得
解得
答:该专业户去年实际生产水稻t,小麦t
(1+15)(吨) (1+10)(吨)
解:设投中个两分球,个罚球,依题意,得
解得
答:投中4个两分球,8个罚球.
解:设该商品进价为元,定价为元,依题意,得
解得
答:该商品进价为元,定价为元.
解:设甲商品进价为元,乙商品进价为 元,依题意,得
解得
答:甲商品进价为元,乙商品进价为 元.
解:设甲带钱,乙带钱,依题意,得
解得
答:甲带钱37.5,乙带钱25.
解:设(1)班有名学生,(2)班有名学生,依题意,得
解得
答: (1)班有名学生,(2)班有名学生;
联合起来购票能省302元。
49102
解:设①⑤两个正方形的边长分别为和,
依题意,得
解得
答:这个正方形的面积为143.
①
②
③
④
⑤
所以
解:方程组有无数个解,方程组所对应的两个一次函数的图象
(两条直线)重合。感悟到由两个函数图象互相重合的方程组
成的方程组有无数个解。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
