人教版九年级下册数学第二十八章锐角三角函数导学案(无答案)
文档属性
| 名称 | 人教版九年级下册数学第二十八章锐角三角函数导学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 12:15:37 | ||
图片预览



文档简介
28.1锐角三角函数(一)
正弦
【学习目标】1、通过探究使学生知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实;2、能根据正弦概念正确进行计算;3、经历当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实,发展学生的形象思维,培养学生由特殊到一般的演绎推理能力。
【教学重点】理解认识正弦(sinA)概念,通过探究使学生知道当锐角固定时,它的对边与斜边的比值是固定值这一事实.
【教学难点】引导学生比较、分析并得出:对任意锐角,它的对边与斜边的比值是固定值的事实。
【教学过程】
一、自主学习:
1.为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行灌溉。现测得斜坡与水平面所成角的度数是30o,为使出水口的高度为35m,那么需要准备多长的水管?
2.在上面的问题中,如果出水口的高度为50m,那么需要准备多长的水管?
结论:在一个直角三角形中,如果一个锐角等于30o,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于____________.
3. 如图,任意画一个Rt△ABC,使∠C=90o,∠A=45o,计算∠A的对边与斜边的比,能得到什么结论?
结论:在一个直角三角形中,如果一个锐角等于45o,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于_____________
4. 一般地,当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?
结论:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是________。
二、知识梳理:
1.认识正弦
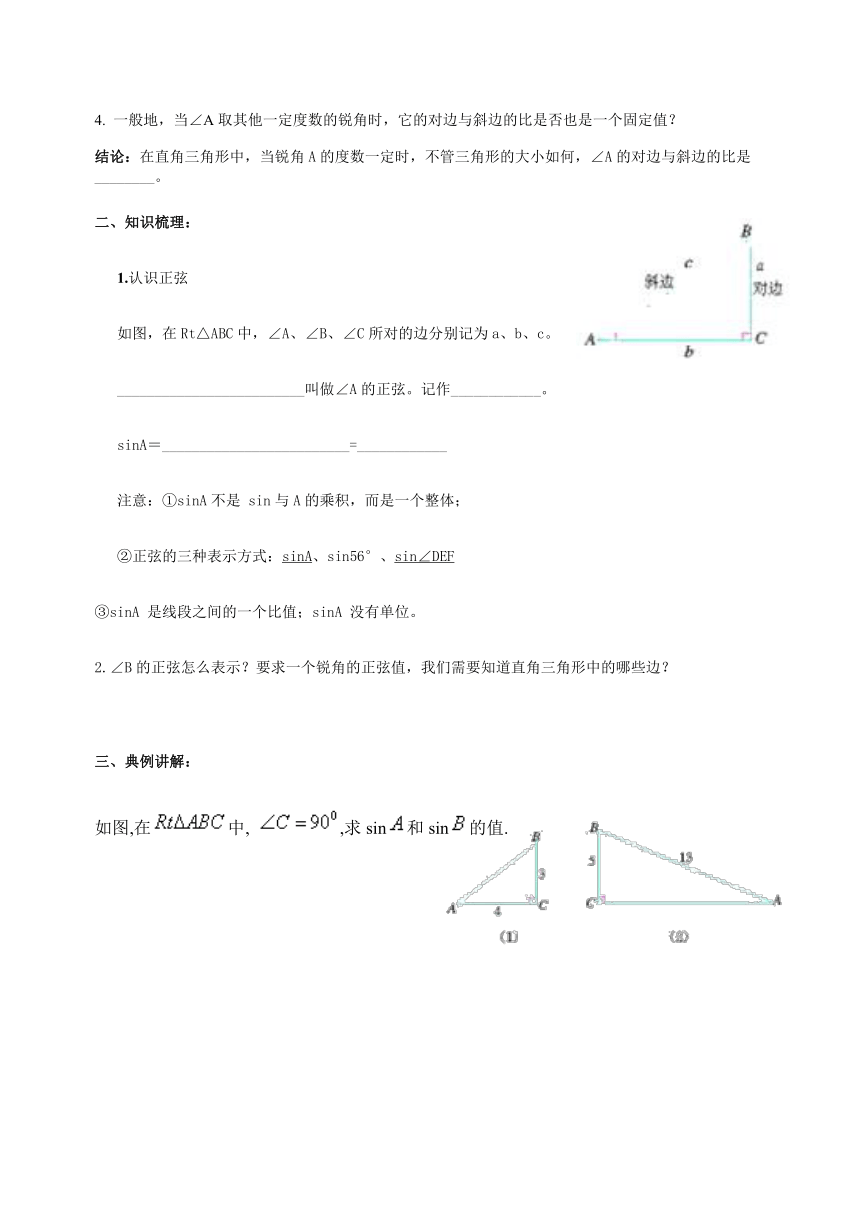
如图,在Rt△ABC中,∠A、∠B、∠C所对的边分别记为a、b、c。
_________________________叫做∠A的正弦。记作____________。
sinA=_________________________=____________
注意:①sinA不是 sin与A的乘积,而是一个整体;
②正弦的三种表示方式:sinA、sin56°、sin∠DEF
③sinA 是线段之间的一个比值;sinA 没有单位。
2.∠B的正弦怎么表示?要求一个锐角的正弦值,我们需要知道直角三角形中的哪些边?
三、典例讲解:
如图,在中, ,求sin和sin的值.
四、巩固练习:
1.三角形在正方形网格纸中的位置如图所示,则sinα的值是﹙ ﹚
A. B. C. D.
2.如图,在直角△ABC中,∠C=90o,若AB=5,AC=4,则sinA=( )
A. B. C. D.
3.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
4. 当∠A=30°时,我们有sinA=sin30°= ;
当∠A=45°时,我们有sinA=sin45°= .
5. 如图,已知点P的坐标是(a,b),则sinα等于( )
A. B. C.
五、小结:
六、反思:
七、作业:练习册
28.1锐角三角函数(二)余弦和正切
【学习目标】1、使学生知道当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实.
2、逐步培养学生观察、比较、分析、概括的思维能力.
【教学重点】理解余弦、正切的概念
【教学难点】熟练运用锐角三角函数的概念进行有关计算
【教学过程】
一、知识链接:
1.正弦的定义:________________________
2.(1)如图,已知AB是⊙O的直径,点C、D在⊙O上,
且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
(2)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
二、自主学习:
1.思考:一般地,当∠A取其他一定度数的锐角时,它的邻边与斜边的比是否也是一个固定值?
如图:Rt△ABC与Rt△A’B’C’,∠C=∠C’=90o,∠B=∠B’=α,那么有什么关系?
分析:
结论:在直角三角形中,当锐角B的度数一定时,不管三角形的大小如何,∠B的邻边与斜边的比也是一个________值。
三、知识梳理:
如图,在Rt△ABC中,∠C=90o,把锐角B的____与_____的比叫做∠B的余弦,记作cosB即cosB=___________,把∠A的_____与_____的比叫做∠A的正切.记作tanA,即tanA=________,________________都叫做∠A的锐角三角函数.
四、典例讲解:
1.如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
2.如图,已知在Rt△ABC中,∠C=90度,D是BC边上一点,AC=6,CD=3,∠ADC=α。
(1)试写出α的正弦、余弦、正切这三个函数值。(2)若∠B∠ADC互余,求BD及AB的长。
3.如图所示,AB是⊙O的直径,C、D是圆 上的两点,C、D不与A、B重合,已知BC=2,tan∠ADC=,求AB。
五、巩固练习:
1.?在中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(?)
A.?B.?C.?D.
本题主要考查锐解三角函数的定义,同学们只要依据的图形,不难写出,从而可判断C正确.
2. 在中,∠C=90°,如果cos A=那么的值为(?)
A.?B.?C.?D.
分析? 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件,可求出;再由,可求出,从而,故应选D.
3、如图:P是∠的边OA上一点,且P点的坐标为(3,4), 则cosα=_____________.
4、已知:如图, Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D
EMBED Equation.3
5、如图所示,在直角坐标系中,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,
sin∠BOA=0.6,(1)求B点的坐标。
(2)求cos∠BAO的值。
六、小结:
七、反思:
八、作业:练习册
28.1锐角三角函数(三)
特殊的三角函数
【学习目标】1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应的锐角度数。2、能熟练计算含有30°、45°、60°角的三角函数的运算式
【教学重点】熟记30°、45°、60°角的三角函数值,熟练计算含有30°、45°、60°角的三角函数的运算式
【教学难点】30°、45°、60°角的三角函数值的推导过程
【教学过程】
一、自主学习:
1.如图∠A=30°,结合图形求出sin30°,cos30°,tan30°;
求出sin60°,cos60°,tan60°
2. 如图∠A=45°,结合图形求出sin45°、cos45°、tan45°
二、知识梳理:
30° 45° 60°
sinA
cosA
tanA
当锐角越来越大时, 的正弦值越来___________,的余弦值越来___________.
当锐角越来越大时, 的正切值越来___________
三、典例讲解:
1.求下列各式的值:
(1) (2)
2.已知∠A为锐角,cosA= ,你能求出sinA和tanA吗?
3.求锐角 a 的度数:
4.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BC=2,BD= .分别求出△ABC、△ACD、△BCD中各锐角.
四、巩固练习:
1.填空: =______
2.在△ABC中,∠A、∠B为锐角,且有 ,则△ABC的形状是________________.
3.计算下列各式的值:
(1) (2)
(3)(4)
4.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tanA的值为( ).
A. B. C. D.
5.在△ABC中,三边之比为a:b:c=1::2,则sinA+tanA等于( ).
A.
6.如图,在△ABC中,已知BC=1+ ,∠B=60°,∠C=45°,求AB的长.
五、小结:
六、反思:
七、作业:练习册
28.1锐角三角函数(四)
计算器与锐角三角函数
【学习目标】1、让学生熟识计算器一些功能键的使用
2、会熟练运用计算器求锐角的三角函数值和由三角函数值来求角
【教学重点】运用计算器处理三角函数中的值或角的问题
【教学难点】运用计算器处理三角函数中的值或角的问题
【教学过程】
一、自主学习:学生自学P67-68:
1、用计算器求锐角的正弦、余弦、正切值
利用求下列三角函数值
sin37°24′=________; sin37°23′=________;cos21°28′=________;
cos38°12′=_______;tan52°=_________;tan36°20′=__________; tan75°17′=_________;
2.熟练掌握用科学计算器由已知三角函数值求出相应的锐角.
例如:sinA=0.9816.∠A= . cosA=0.8607,∠A= ;
tanA=0.1890,∠A= ; tanA=56.78,∠A= .
二、巩固练习:
1.用计算器求sin15°、sin25°、sin35°、sin45°、sin55°、sin65°、sin75°、sin85°的值,确定sinα的值随锐角α变化的规律,根据这个规律判断:若,则( )
A、 30°<α<60° B、30°<α<90° C、0°<α<60° D、60°<α<90°
2.用计算器求下列锐角三角函数值,并填入表中:
锐角A … 15° 18° 20° 22° … 80° 82° 84° …
sinA
cosA
tanA
随着锐角A的度数不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?你能说明自己的结论吗?
三、小结:
四、反思:
五、作业:练习册
28.1锐角三角函数(五)
锐角三角函数间的关系
【学习目标】了解一个锐角的正弦(余弦)值与它的余角的余弦(正弦)值之间的关系;了解同一个锐角正弦与余弦之间的关系;了解正切与正弦、余弦的关系;了解三角函数值随锐角的变化而变化的情况。
【教学重点】三个锐角三角函数间几个简单关系
【教学难点】能独立根据三角函数的定义推导出三个锐角三角函数间几个简单关系
【教学过程】
一、知识链接:
正弦、余弦、正切的定义:
二、新知探索:
1、从定义可以看出与有什么关系?与呢?满足这种关系的与又是什么关系呢?
2、利用定义及勾股定理你还能发现与的关系吗?
3、再试试看与和存在特殊关系吗?
4、在正弦中它的值随锐角的增大而增大还是随锐角的增大而减少?为什么?余弦呢?正切呢?
三、典例讲解:
1.判断:①? 对于任意锐角α,都有0<sinα<1和0<cosα<1 (??? )
② 对于任意锐角α1,α2,如果α1<α2,那么cosα1<cosα2????????? (??? )
③ 如果sinα1<sinα2,那么锐角α1<锐角α2I???????????????????????????????????? ????? (??? )
④ 如果cosα1<cosα2,那么锐角α1>锐角α2??????????????????????????????? (??? )
2.在Rt△ABC中,下列式子中不一定成立的是______
A.sinA=sinB B.cosA=sinB C.sinA=cosB D.sin(A+B)=sinC
3.如图1、2,锐角的正弦值和余弦值都是随着锐角的确定而确定、变化而变化的,试探究随着锐角度数的增大,它的正弦值和余弦值变化的规律:随着锐角度数的增大,它的正弦值逐渐_____________,它的余弦值逐渐_______________。
(2)根据你探索到的规律,试比较18°、34°、50°、
62°、88°这些锐角的正弦值和余弦值的大小。
(3)比较大小,(在空格处填写“<”“>“=”)??
若α=45°,则sinα____cosα;??
若α<45°,则sinα____cosα;??
若α>45°,则sinα____cosα;
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin??10°、cos30°、sin50°、cos 70°。
四、巩固练习:
1.如图1,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是____________。
图 1 图2
2.如图所示,在直角坐标系中,四边形OABC是直角梯形,BC∥OA,⊙P分别与OA、OC、BC相切于点E、D、B,与AB交于点F。已知A(2,0),B(1,2),求tan∠FDE值。
3.已知,如图所示,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD。
(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;
(3)若⊙O的半径为5,AF=7.5,求tan∠ABF的值。
五、小结:
六、反思:
七、作业:练习册
28.2.1解直角三角形
【学习目标】?1、理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.2、通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力.?3、渗透数形结合的数学思想,培养良好的学习习惯.
【教学重点】直角三角形的解法.
【教学难点】三角函数在解直角三角形中的灵活运用.
【教学过程】
一、知识链接:
?1.在三角形中共有几个元素?
?2.Rt△ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
(1)边角之间关系:
(2)三边之间关系:
?(3)锐角之间关系:
二、自主学习: 学生自学P72-73,完成下列内容:
?1.我们已掌握Rt△ABC的边角关系、三边关系、角角关系,利用这些关系,由直角三角形中的_____元素,求出其余_____元素的过程,叫做解直角三角形。
2.在直角三角形中,知道其中的_____元素(至少有一个是_____)后,就可求出其余的_________元素.
三、知识梳理:
1.一般地,直角三角形中,除直角外,共有_____个元素,即_________和________个锐角。由直角三角形中的_______元素(至少有 ______条边),求出其余_________元素的过程(知二求三),叫做解直角三角形。
2.一个直角三角形可解,则其面积可求。但在一个解直角三角形的题中,如无特别说明,则不包括求面积。
3.在Rt△ABC中,∠C=90°, a、b、c分别是∠A、∠B、∠C所对的边,完成下列表格。
? a b c A B
1 已知 已知 c=_______ tanA=_______ tanB=_______
2 已知 b=_________ 已知 sinA=________ cosB=_________
3 已知 b=________ c=_______ 已知 ∠B=_________
4 已知 b=a?______ c=________ ∠A=_________ 已知
5 a=______ 已知 已知 cosA=_______ sinB=______
6 a=b?____ 已知 C=________ 已知 ∠B=_________
7 a=_______ 已知 C=________ ∠A=_________ 已知
8 a=c?sinA b=c?cosA 已知 已知 ∠B=_________
9 a=c?_____ b=c?______ 已知 ∠A=_________ 已知
10 a=_______ b=_______ c=_______ 已知 已知
四、典例讲解:?
1. 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=,a=,解这个直角三角形.
注:解直角三角形,就是把所有未知元素求出来的过程,不是只求单一的一条未知边或一个未知角。
2.如图所示,在△ABC中,∠C=90°,sinA=0.4,D为AC上一点,∠BDC=45°,DC=6,求AB的长。
3.如图所示,在△ABC中,∠A=60°, ∠B=45°,AB=8, 求△ABC的面积(结果保留根号)
五、巩固练习:
1.如图所示,在△ABC中,AD是BC边上的高,E为边AC的中点,BC=14,AD=12,sinB=0.8,求:(1)线段CD的长;(2)tan∠EDC的值.
2.如图所示,在Rt△ABC,∠C=90°,D是BC的中点,DE⊥AB于点E,tanB=0.5,AE=9,求DE的长。
3. 如图所示,在Rt△ABC,∠ACB=90°,CD是斜边AB是的中点,过点A作AE⊥CD。AE分别与CD,CB相交于点H、E,AH=2CH。(1)求sinB的值;(2)如果,求BE的值。
六、小结:
七、反思:
八、作业:练习册
28.2.2应用举例(一)
仰角与俯角
【学习目标】1、会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决.2、逐步培养分析问题、解决问题的能力.3、渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
【教学重点】要求学生善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
【教学难点】实际问题转化成数学模型
【教学过程】
一、知识连接:如图,在Rt△ABC中,a,b分别是∠A、∠B的对边,c为斜边,如果已知两个元素a、∠B,就可以求出其余三个未知元素b、c、∠A。(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程;
第一步: 用关系式 求出
第二步: 用关系式 求出
第三步:
用关系式 求出
(2)请你分别给出a、∠B的一个具体数值,然后按照(1)中的思路,求出b、c、∠A的值。
二、自主学习: 自学P74-75,完成下列内容:
1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看平面控制点B的俯角α=16°31’,求飞行点A到控制点B的距离。(精确到1m,参考数据:sin16°31’=0.2843)
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,求B,C两地之间的距离。
三、知识梳理:利用解直角三角形的知识解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题;
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;(4)得到实际问题的答案
四、典例讲解:
1.如图,小山顶上有一信号塔AB,山坡BC的倾角为30°,现为了测量塔高AB,测量人员选择山脚C处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100m到达E处,再测得塔顶仰角为60°,求塔高AB。(结果保留整数,)
2.九一班数学兴趣组为了测量河对岸的两座古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,求古塔A、B的距离。
五、巩固练习:
1.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60 °,否则就有危险,那么梯子的长至少为_______米。
2.被誉为东昌三宝之首的铁塔,始建于北宋时期,是山东聊城市现存的最古老的建筑,铁塔由塔身和塔座两部分组成(如图)。为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6m,CD的长为6m,CD所在的水平线CG⊥EF于点G,求铁塔EF的高(结果精确到0.1m)。
六、小结:
七、反思:
八、作业:练习册
28.2.2应用举例(二)
方向角
【学习目标】1、了解方向角的命名特点,能准确把握所指的方位角是指哪一个;2、逐步培养分析问题、解决问题的能力;渗透数形结合的数学思想和方法.3、巩固用三角函数有关知识解决问题,学会解决方位角问题.
【教学重点】用三角函数有关知识解决方位角问题
【教学难点】学会准确分析问题并将实际问题转化成数学模型
【教学过程】
一、知识链接:如图1所示,平地上一幢建筑物与铁塔,图2为其示意图。建筑物AB与铁塔CD都垂直于地面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°。求铁塔CD的高度。(结果保留根号)
二、自主学习: 自学P76,完成下列内容:
1.若乙、丙都在甲的北偏东70°方向上,乙在丁的正北方向上,且到丙、丁的距离相同,则丙在丁的北偏东_________的方向上。
2.如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里。
(1)求船P到海岸线MN的距离(精确到0.1海里);
(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处。(参考数据:sin32°≈0.5299,sin58°≈0.8480,sin55°≈0.8191)
三、典例讲解:
1.如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为海里,在A处看灯塔C在货轮的北偏西30°,距离为海里,货轮由A处向正北航行到D处,再看灯塔B在南偏东60°。(1)求A处与D处的距离;(2)求C处与D处的距离。
2. 一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上。
(1)求灯塔P到轮船航线的距离PD是多少海里?(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分针到达D处,求轮船每小时航行多少海里?(结果保留到个位,参考数据:).
四、巩固练习:
1. 如图,甲、乙两只捕捞船同时从A港出海捕鱼.甲船以每小时千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
2.台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内
形成气旋风暴,有极强的破坏力。据气象台观测,某台风最大风力为12级,每远离台风中心20km,风力就会减弱一级。如图所示,该台风中心(B点)现正在某城市A的正南方向220km处以15km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变。若城市所受风力达到或超过4级,则称为受台风影响。
(1)该城市是否会受到这次台风的影响?请说明理由;
(2)若受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受台风影响的最大风力为几级?
五、小结:
六、反思:
七、作业:练习册
28.2.2应用举例(三)
山坡的坡度
【学习目标】1、巩固用三角函数有关知识解决问题,学会解决坡度问题.2、逐步培养分析问题、解决问题的能力;渗透数形结合的数学思想和方法.3、培养用数学的意识,渗透理论联系实际的观点.
【教学重点】解决有关坡度的实际问题.
【教学难点】理解坡度的有关术语.
【教学过程】
一、知识链接:如图,海上有一灯塔P,在它周围6海里内有暗礁。一艘轮船以18海里/小时的速度由西向东方向航行,行至点A处测得灯塔P在它北偏东60°的方向上。继续向东航行20分钟后,到达B处又测得灯塔P在它北偏东45°的方向上。如果轮船不改变方向继续前进,有没有触礁的危险?
二、知识梳理:
1.坡角:坡面与水平面所成的夹角。如图中的α。
坡度:我们通常把坡面的铅直高度h和水平宽度的比叫做坡度,坡度也可以写成的形式。
2.坡度与坡角的关系:
三、典例讲解:
如图,拦水坝的横断面为梯形ABCD,(图中是指坡面的铅直高度DE与水平宽度CE的比),.。
求:(1)∠C的度数;(2)拦水坝的横断面ABCD的面积。
四、巩固练习:
1.如图,在坡角为30°的楼梯的表面铺地毯,则地毯的长度至少需要多少米?
2.如图所示,河堤横断面迎水坡AB的坡比是,堤高BC=5m,则坡面AB的长度是( )
EMBED Equation.3
3.如图,一段河坝的横断面为梯形ABCD,试根据图中所给出的数据,求出坡角α和坝底AD的长。
(i=CE:CD,单位:m)
4. 如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得高压电线杆顶端点D的仰角为30°。已知地面CB宽30m,求高压电线杆CD的高度。(结果保留三个有效数字,)
5.水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD,如图所示,已知迎水坡AB的长度为16m,∠B=60°,背水坡面CD的长为,加固后大坝的横截面积为梯形ABED,CE的长为8m。
(1)已知需加固的大坝长为150m,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度。
6.为方便行人横过马路,打算修建一座高5m的过街天桥。已知天桥的斜面坡度为1:1.5,计算斜坡AB的长度(结果取整数)。
五、小结:
六、反思:
七、作业:练习册
第28章 《锐角三角函数》整理与复习
【学习目标】1.会根据三角函数的定义,求三角函数值;2.能够熟记特殊角的三角函数值;3.解直角三角形及其应用。
【教学重点】会根据三角函数的定义,求三角函数值;能够熟记特殊角的三角函数值;解直角三角形及其应用。
【教学难点】会运用方程思想求直角三角形的某些未知元素,会运用转化思想通过添加辅助线化不规则图形为规则图形,构建直角三角形求解。
【教学过程】
一、知识梳理:(一)锐角三角函数定义
◆知识点归纳
1.如图所示,在Rt△ABC中,∠C=90°.
①=______, =______;
②=______, =______;
③=______, =______.
2.特殊角的三角函数值.
a sina cosa tana
30°
45°
60°
由图可知,①取值范围:
若∠a是锐角,则 <sina< , <cosa< ,tana ;
②增减性:
正弦、正切值是随着角度的增大而 ,余弦是随着角度的增大而 .
当 时,sina<cosa, 当 时,sina>cosa,
③几个重要关系式条件:当∠A为锐角时有:
, ????????????=1,sinA=( ),cosA=( )
(二)解直角三角形
◆知识点归纳
1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示):
在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c,
①三边之间的等量关系:
__________________________________.
②两锐角之间的关系:
__________________________________.
③直角三角形中成比例的线段(如图所示)
在Rt△ABC中,∠C=90°,CD⊥AB于D.
CD2=_________;AC2=_________;BC2=_________;AC·BC=_________
(三)解直角三角形的实际运用
1、图中角可以看作是点A的 角
也可看作是点B的 角;
2.(1)坡度(或坡比)是坡面的 高度(h)和 长度(l)的比。
记作i,即i = ;
(2)坡角:坡面与水平面的夹角。记作α,有i==tanα
(3)坡度与坡角的关系:坡度越大,坡角α就越 ,坡面就越
二、基础练习:
1.已知Rt△中,若cos,则
2.Rt△中,,那么
3.已知,且为锐角,则的取值范围是 ;
4.已知:∠是锐角,,则的度数是
5.当锐角A的时,∠A的值为( )
A 小于 B 小于 C 大于 D 大于
6.在⊿ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况( )
A 都扩大2倍 B 都缩小2倍 C 都不变 D 不确定
7.已知为锐角,若,= ;若,则
8.若,则锐角的度数为( )
A.200 B.300 C.400 D.500
9.如果 ,那么△ABC是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形
10.计算(1)
(2) (3)
11.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价30元,则购买这种草皮至少需要( )
A.13500元 B.6750元 C.4500元 D.9000元
12.等腰三角形的腰长为2cm,面积为1 cm2,则顶角的度数为
14.如图,AC⊥BC,cos∠ADC=,∠B=30°AD=10,求 BD的长.
15. 某水库大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个坡角的和为 ( ) A B C D
16. 永乐桥摩天轮是天津市的标志性景观之一.某校 数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为.求该兴趣小组测得的摩天轮的高度AB(,结果保留整数).
解:
三、典例讲解:
1.2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图所示,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60, cos37°≈0.80,tan37°≈0.75,≈1.73)
2.如图所示,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1︰,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)
四、巩固练习:
1.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕的长是( )
第1题, 第2题 第3题 第4题
A.cm B. cm C.cm D.2cm
2.如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是( )
A.3 B.5 C. D.
3.如图,在等腰Rt△ABC中,∠C=90o,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为( ) A.2 B. C. D.1
4.如图,的正切值等于 。
4.如图,已知四边形ABCD,∠ABC=120 o ,AD⊥BA,CD⊥BC,,求四边形ABCD的面积。
5.如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E。(1)求证:∠EPD=∠EDO;
(2)若PC=6,,求OE的长。
五、小结:
六、反思:
七、作业:练习册
由条件:a、∠B
由条件:
由条件:
