北师大小学数学四下《数学好玩密铺》(共30张PPT)
文档属性
| 名称 | 北师大小学数学四下《数学好玩密铺》(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 22:24:38 | ||
图片预览









文档简介
(共30张PPT)
俄罗斯方块
G D
OO
叶集二小
自然艺术家
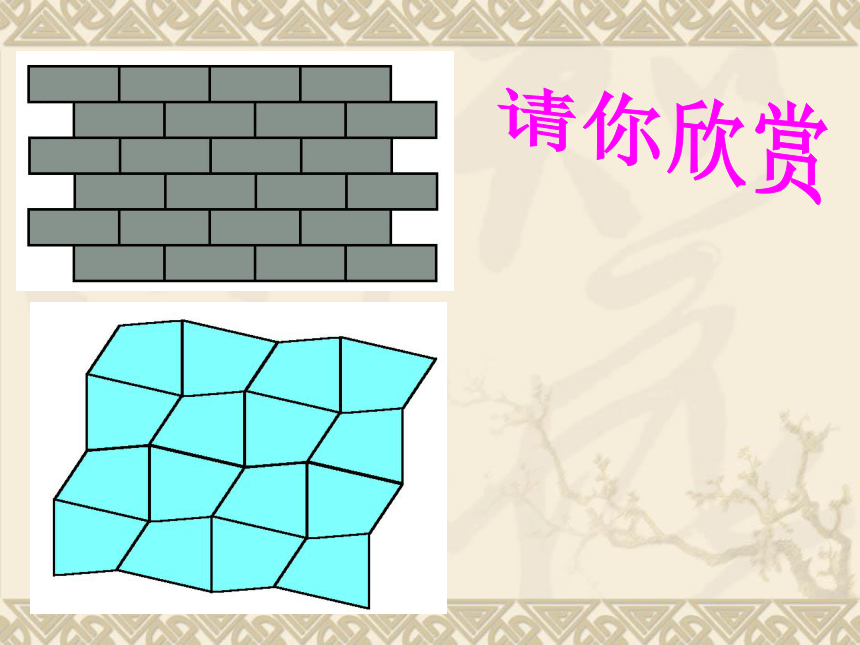
这些图案都是用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,这叫做平面图形的密铺,又称做平面图形的镶嵌。
观察与理解
思考与操作
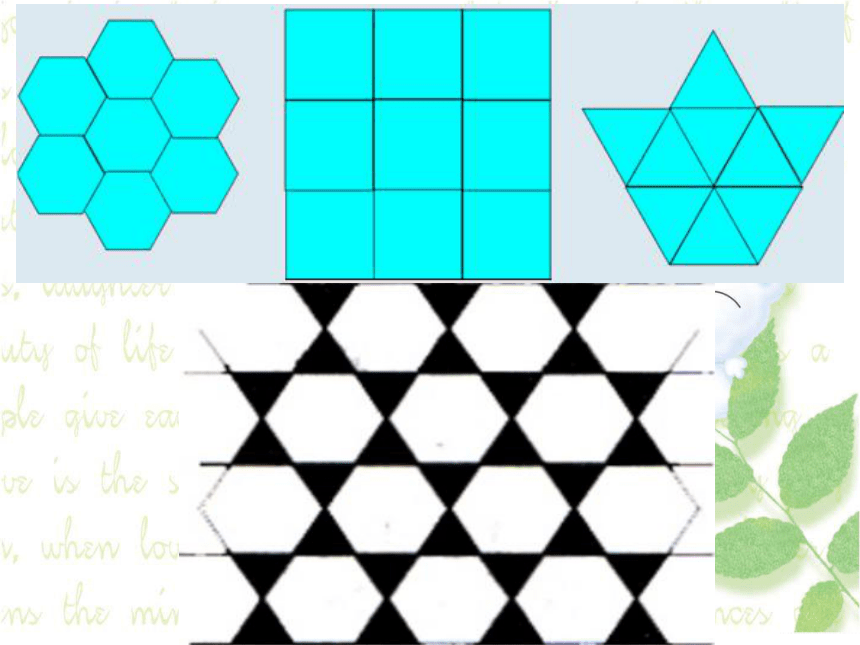
经过操作,哪些图形可以密铺呢?
做一做
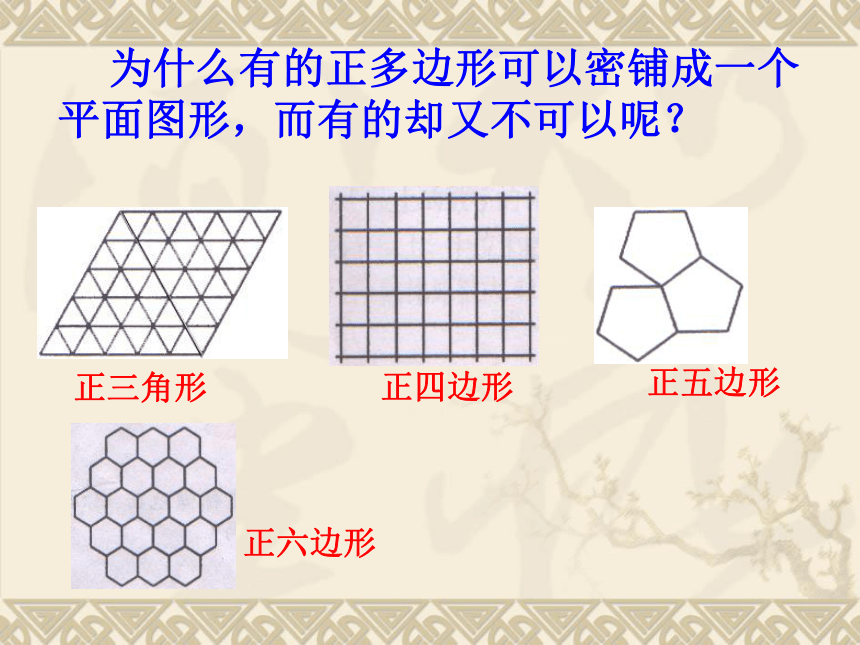
为什么有的正多边形可以密铺成一个平面图形,而有的却又不可以呢?
正三角形
正五边形
正四边形
正六边形
正方形为什么能密铺?
90度
×4
=360度
结论:任意全等的三角形能密铺
三角形的每个内角在每个拼接点处出现两次,所以180°×2=360°
用形状、大小完全相同的任意四边形能否密铺?
四边形的每个内角在每个拼接点处出现一次,共:360°。
单独一种多边形密铺探索
啊!拼不了啦,为什么呢?你能说说原因吗?
1
2
3
108度
×( ?)
≠360度
108度
120度
×3
=360度
120度
正六边形可以密铺
小结:
同学们,通过我们的实验,大家可以发现:每个拼接点处,当几个多边形的内角和能组成360度,则可以密铺(比如三角形、四边形、正六边形),否则将无法进行密铺的。
用你掌握的知识来判断下面正多边形能否密铺.
正八边形(一个内角是135度)
正九边形(一个内角是140度)
正十边形(一个内角是144度)
不能密铺
不能密铺
不能密铺
密铺的含义
今天的收获:
哪些图形可以密铺: 三角形、四边形和正六边形都可以单独密铺。
一种多边形能否密铺关键看它的内角是否能组成360度。
阿罕伯拉宫
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
密铺或镶嵌艺术离我们很遥远吗?
这是密铺作品,这也是镶嵌,它是怎么样做出来的呢?
请往下看,实际上是很简单的
你看懂了吗?实际上是用正方形“剪”“拼”出来的
你能利用密铺的知识设计一幅地砖图案吗?试试看吧!
俄罗斯方块
G D
OO
叶集二小
自然艺术家
这些图案都是用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,这叫做平面图形的密铺,又称做平面图形的镶嵌。
观察与理解
思考与操作
经过操作,哪些图形可以密铺呢?
做一做
为什么有的正多边形可以密铺成一个平面图形,而有的却又不可以呢?
正三角形
正五边形
正四边形
正六边形
正方形为什么能密铺?
90度
×4
=360度
结论:任意全等的三角形能密铺
三角形的每个内角在每个拼接点处出现两次,所以180°×2=360°
用形状、大小完全相同的任意四边形能否密铺?
四边形的每个内角在每个拼接点处出现一次,共:360°。
单独一种多边形密铺探索
啊!拼不了啦,为什么呢?你能说说原因吗?
1
2
3
108度
×( ?)
≠360度
108度
120度
×3
=360度
120度
正六边形可以密铺
小结:
同学们,通过我们的实验,大家可以发现:每个拼接点处,当几个多边形的内角和能组成360度,则可以密铺(比如三角形、四边形、正六边形),否则将无法进行密铺的。
用你掌握的知识来判断下面正多边形能否密铺.
正八边形(一个内角是135度)
正九边形(一个内角是140度)
正十边形(一个内角是144度)
不能密铺
不能密铺
不能密铺
密铺的含义
今天的收获:
哪些图形可以密铺: 三角形、四边形和正六边形都可以单独密铺。
一种多边形能否密铺关键看它的内角是否能组成360度。
阿罕伯拉宫
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
密铺或镶嵌艺术离我们很遥远吗?
这是密铺作品,这也是镶嵌,它是怎么样做出来的呢?
请往下看,实际上是很简单的
你看懂了吗?实际上是用正方形“剪”“拼”出来的
你能利用密铺的知识设计一幅地砖图案吗?试试看吧!
