2019年沪科版九年级上册数学《第23章 解直角三角形》单元测试卷(解析版)
文档属性
| 名称 | 2019年沪科版九年级上册数学《第23章 解直角三角形》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-31 00:00:00 | ||
图片预览



文档简介
2019年沪科版九年级上册数学《第23章 解直角三角形》单元测试卷
一.选择题(共10小题)
1.如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan∠AEB的值等于( )
A.3 B.2 C. D.
2.已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2﹣3x+1=0的两根,则△ABC是( )
A.锐角三角形
B.直角三角形或钝角三角形
C.钝角三角形
D.等边三角形
3.已知<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80° B.10°<α<80° C.60°<α<80° D.10°<α<60°
4.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
5.α为锐角,若sinα+cosα=,则sinα﹣cosα的值为( )
A. B.± C. D.0
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
7.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
8.在△ABC中,若||=0,且∠B,∠C都是锐角,则∠A的度数是( )
A.15° B.60° C.75° D.30°
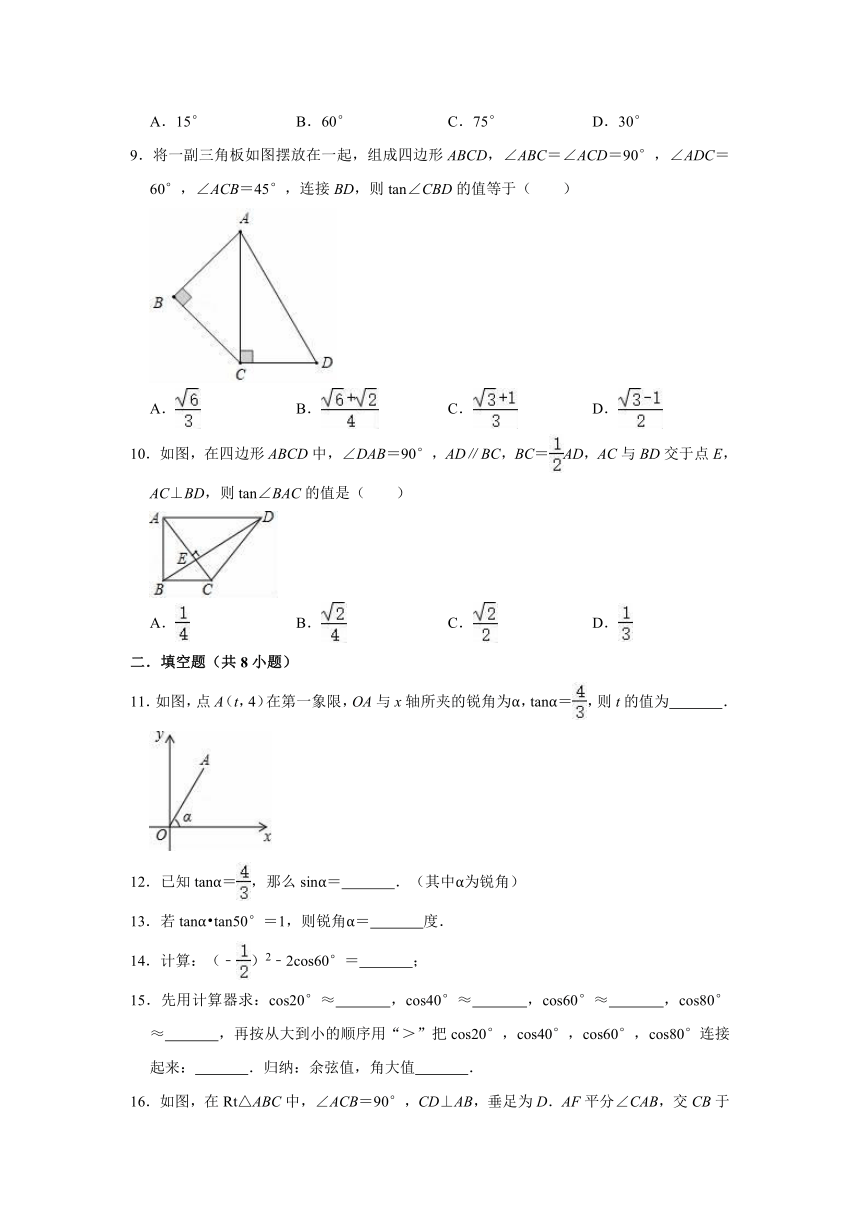
9.将一副三角板如图摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值等于( )
A. B. C. D.
10.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
二.填空题(共8小题)
11.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值为 .
12.已知tanα=,那么sinα= .(其中α为锐角)
13.若tanα?tan50°=1,则锐角α= 度.
14.计算:(﹣)2﹣2cos60°= ;
15.先用计算器求:cos20°≈ ,cos40°≈ ,cos60°≈ ,cos80°≈ ,再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,cos80°连接起来: .归纳:余弦值,角大值 .
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
17.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为 米(结果保留根号).
18.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
三.解答题(共8小题)
19.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
20.在Rt△ABC中,∠ACB=90°
(1)tanA与sinA,cosA之间有什么关系?并说明理由.
(2)若=,求tanA的值.
21.计算:tan30°cos60°+tan45°cos30°.
22.已知三角函数值,求锐角(精确到1″).
(1)已知sinα=0.5018,求锐角α;
(2)已知tanθ=5,求锐角θ.
23.如图,在△ABC中;AD⊥BC,AB=20,AC=15,CD=9
(1)求BD的长;
(2)求∠BAC的度数.
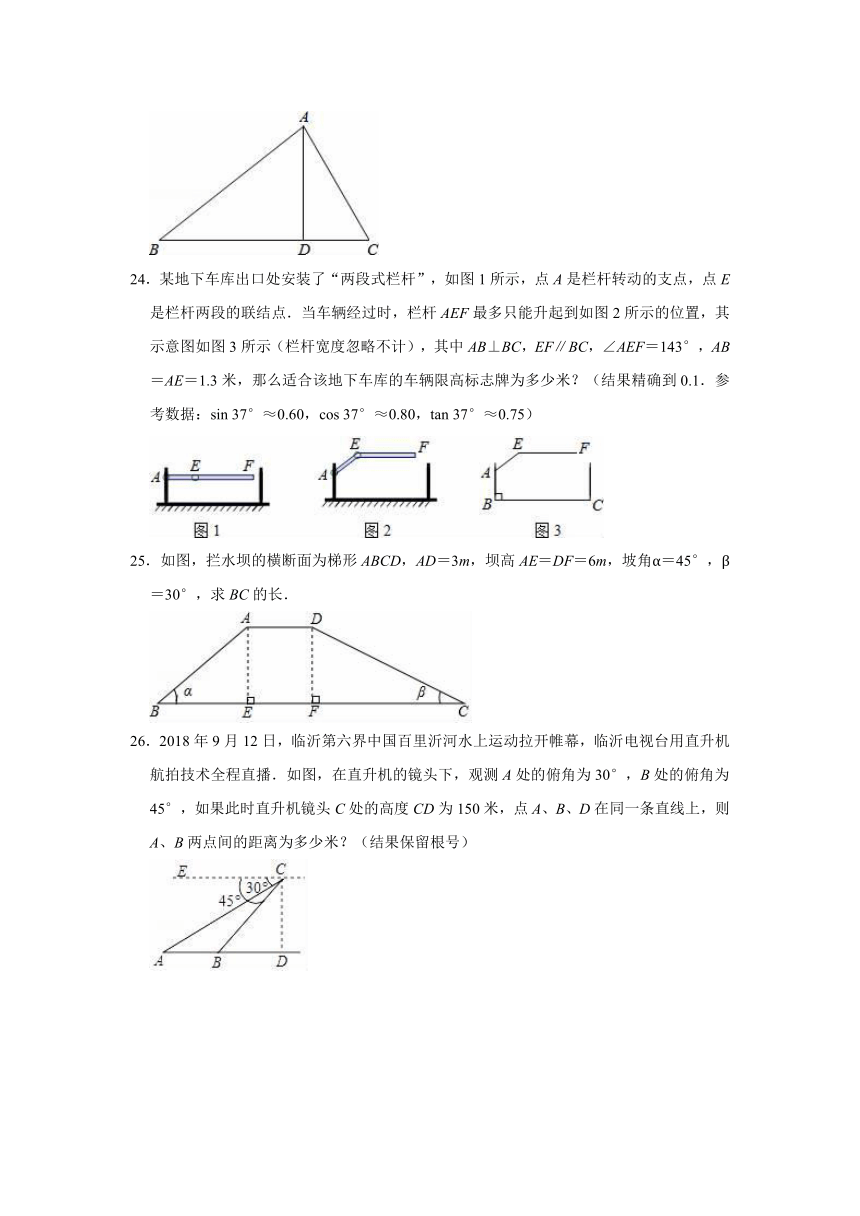
24.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
25.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.
26.2018年9月12日,临沂第六界中国百里沂河水上运动拉开帷幕,临沂电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为150米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)
2019年沪科版九年级上册数学《第23章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan∠AEB的值等于( )
A.3 B.2 C. D.
【分析】过B作DC的平行线交DA的延长线于M,在DM的延长线上取MN=CE.
根据全等三角形及直角三角形的性质求出∠BNM两直角边的比,即可解答.
【解答】解:过B作DC的平行线交DA的延长线于M,在DM的延长线上取MN=CE.
则四边形MDCB为正方形,易得△MNB≌△CEB,
∴BE=BN.∴∠NBE=90°.
∵∠ABE=45°,∴∠ABE=∠ABN,
∴△NAB≌△EAB.
设EC=MN=x,AD=a,则AM=a,DE=2a﹣x,AE=AN=a+x,
∵AD2+DE2=AE2,
∴a2+(2a﹣x)2=(a+x)2,
∴x=a.
∴tan∠AEB=tan∠BNM==3.
故选:A.
【点评】本题考查的是锐角三角函数的定义,解答此题的关键是作出辅助线,构造出直角三角形,利用数形结合解答.
2.已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2﹣3x+1=0的两根,则△ABC是( )
A.锐角三角形
B.直角三角形或钝角三角形
C.钝角三角形
D.等边三角形
【分析】先解出方程的两根,讨论sinα,tanβ的值.∵在三角形中,角的范围是(0,180°),∴sinα必大于0,此时只要考虑tanβ的值即可,若tanβ>0,则β为锐角;tanβ小于0,则β为钝角.再把x的两个值分别代入sinα,tanβ中,可求出α,β的值,从而判断△ABC的形状.
【解答】解:由2x2﹣3x+1=0得:(2x﹣1)(x﹣1)=0,∴x=或x=1.
∴sinα>0,tanβ>0
若sinα=,tanβ=1,则α=30°,β=45°,γ=180°﹣30°﹣45°=105°,
∴△ABC为钝角三角形.
若sinα=1,tanβ=,则α=90°,β<90°,△ABC为直角三角形.
故选:B.
【点评】本题易在α,β上的取值出错,学生常常解出方程的两根后不知道如何判断,因此在解答时我们可对x的值分类讨论,从而判断出△ABC的形状.
3.已知<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80° B.10°<α<80° C.60°<α<80° D.10°<α<60°
【分析】由cos60°=,sin80°=cos10°,锐角α的余弦值随着α的变大而减小,可得出α的范围,从而可得答案.
【解答】解:∵cos60°=,<cosα<sin80°
锐角α的余弦值随着α的变大而减小,
故α<60°
∵sin80°=cos10°
∴10°<α<60°
故选:D.
【点评】本题考查了锐角三角函数的增减变化,明确锐角三角函数的增减变化以及特殊角的三角函数值,是解题的关键.
4.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
【分析】cosA=sin(90°﹣A),再根据余弦函数随角增大而减小进行分析.
【解答】解:∵cosA=sin(90°﹣A),余弦函数随角增大而减小,
∴当0°<∠A<45°时,sinA<cosA,即sinA﹣cosA<0.
故选:B.
【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.
5.α为锐角,若sinα+cosα=,则sinα﹣cosα的值为( )
A. B.± C. D.0
【分析】将两式分别两边平方,利用sin2α+cos2α=1,求出sinαcosα的值,解答即可.
【解答】解:∵sinα+cosα=,
∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0.
∴sinα﹣cosα=0.
故选:D.
【点评】本题利用了同角的三角函数的关系sin2α+cos2α=1来进行化简求值的.
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
【分析】本题可根据非负数的性质“两个非负数相加和为0,这两个非负数的值都为0.”分别求出∠A、∠B的值.然后用三角形内角和定理即可求出∠C的值.
【解答】解:∵|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,=cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选:C.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握二次根式、绝对值、非负数等考点的运算.
7.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
【分析】根据非负数的性质列出关系式,根据特殊角的三角函数值求出∠A、∠B的度数,根据三角形内角和定理计算即可.
【解答】解:由题意得,sinA﹣=0,﹣cosB=0,
即sinA=,=cosB,
解得,∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°,
故选:C.
【点评】本题考查的是非负数的性质的应用、特殊角的三角函数值的计算和三角形内角和定理的应用,熟记特殊角的三角函数值是解题的关键.
8.在△ABC中,若||=0,且∠B,∠C都是锐角,则∠A的度数是( )
A.15° B.60° C.75° D.30°
【分析】先根据非负数的性质求出sinB及cosC的值,再由特殊角的三角函数值解答即可.
【解答】解:∵ +|﹣cosC|=0,
∴sinB﹣=0;﹣cosC=0.
即sinB=;cosC=.
∴∠B=45°,∠C=60°.
∴∠A=180°﹣∠B﹣∠C=180°﹣45°﹣60°=75°.
故选:C.
【点评】此题涉及到非负数的性质、特殊角的三角函数值及三角形内角和定理.
9.将一副三角板如图摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值等于( )
A. B. C. D.
【分析】如图所示,连接BD,过点D作DE垂直于BC的延长线于点E,构造直角三角形,将∠CBD置于直角三角形中,设CE为1,根据特殊直角三角形分别求得线段CD、AC、BC,从而按正切函数的定义可解.
【解答】解:如图所示,连接BD,过点D作DE垂直于BC的延长线于点E
∵在Rt△ABC中,∠ACB=45°,在Rt△ACD中,∠ACD=90°
∴∠DCE=45°,
∵DE⊥CE
∴∠CED=90°,∠CDE=45°
∴设DE=CE=1,则CD=
在Rt△ACD中,
∵∠CAD=30°,
∴tan∠CAD=,则AC=,
在Rt△ABC中,∠BAC=∠BCA=45°
∴BC=,
∴在Rt△BED中,tan∠CBD===
故选:D.
【点评】本题考查了用定义求三角函数,同时考查了特殊角的三角函数值,如何作辅助线,是解题的关键.
10.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
【分析】证明△ABC∽△DAB,得出=,证出AD=2BC,得出AB2=BC×AD=BC×2BC=2BC2,因此AB=BC,在Rt△ABC中,由三角函数定义即可得出答案.
【解答】解:∵AD∥BC,∠DAB=90°,
∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB+∠EAD=90°,
∴∠BAC=∠ADB,
∴△ABC∽△DAB,
∴=,
∵BC=AD,
∴AD=2BC,
∴AB2=BC×AD=BC×2BC=2BC2,
∴AB=BC,
在Rt△ABC中,tan∠BAC===;
故选:C.
【点评】本题考查了平行线的性质、相似三角形的判定与性质以及解直角三角形的应用等知识;熟练掌握解直角三角形,证明三角形相似是解题的关键.
二.填空题(共8小题)
11.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值为 3 .
【分析】根据点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,可以求得t的值.
【解答】解:∵点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,
∴tanα==.
解得t=3.
故答案为:3.
【点评】本题考查锐角三角函数,解题的关键是明确锐角三角函数的定义和第一象限点的特点.
12.已知tanα=,那么sinα= .(其中α为锐角)
【分析】根据锐角三角函数的定义,设∠A=α,放在直角三角形ACB中,设BC=4x,AC=3x,由勾股定理求出AB,再根据锐角三角函数的定义求出即可.
【解答】解:
∵∠C=90°,∠A=α,
∵tanα==,
设BC=4x,AC=3x,
由勾股定理得:AB==5x,
∴sinα=sin∠A===.
故答案为:.
【点评】本题考查了勾股定理,锐角三角函数等知识点,解此题的关键是把所求角放在直角三角形中,思路是根据锐角三角函数的定义和直角三角形求出即可.题目较好,难度不大.
13.若tanα?tan50°=1,则锐角α= 40 度.
【分析】根据锐角三角函数的定义得出如果tanα?tan50°=1,那么α+50°=90°,即可求出答案.
【解答】解:∵在△ACB中∠C=90°,∠A=α,∠B=50°,
∵tanA=,tanB=,
∴tanA?tanB=×=1,
∴∠A+∠B=90°,
∵tanα?tan50°=1,
∴α=90°﹣50°=40°.
故答案为:40.
【点评】本题主要考查对互余两角的三角函数的关系,锐角三角函数的定义等知识点的理解和掌握,能熟练地运用性质进行计算是解此题的关键.
14.计算:(﹣)2﹣2cos60°= ﹣ ;
【分析】先算平方,特殊角的三角函数值,再算减法即可求解.
【解答】解:(﹣)2﹣2cos60°
=﹣2×
=﹣1
=﹣.
故答案为:﹣.
【点评】考查了特殊角的三角函数值,关键是熟练掌握60°的余弦值.
15.先用计算器求:cos20°≈ 0.9397 ,cos40°≈ 0.7660 ,cos60°≈ 0.5 ,cos80°≈ 0.1736 ,再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,cos80°连接起来: cos20°>cos40°>cos60°>cos80° .归纳:余弦值,角大值 小 .
【分析】利用计算器分别计算各个三角函数值,然后根据角的增大,来观察余弦数值的变化.
【解答】解:利用计算器可算出:cos20°≈0.9397,cos40°≈0.7660,cos60°=0.5,cos80°≈0.1736,
∴cos20°>cos40°>cos60°>cos80°
∴在锐角范围内,余弦函数值随着角度的增大而减小,即余弦值,角大值小.
故答案是0.9397,0.7660,0.5,0.1736,小.
【点评】本题考查了计算器求三角函数值,注意小数点后保留3位或4位有效数字.
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
【分析】先由AF平分∠CAB,CD⊥AB,过点E作EG垂直于AC,利用角平分线的性质定理得EG等于DE,易得Rt△AED全等于Rt△AEG以及∠DCA等于∠B,从而求得AD,AG,CG,然后在Rt△CEG中,由勾股定理求出EG,即为DE的长度.
【解答】解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
【点评】本题综合运用了角平分线的性质定理,全等三角形判断,勾股定理等知识,难度较大.
17.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为 2+2 米(结果保留根号).
【分析】本题需要分段求出巷子被分成的两部分,再加起来即可.先在直角三角形ABC中,用正切和正弦,分别求出BC和AC(即梯子的长度),然后再在直角三角形DCE中,用∠DCE的余弦求出DC,然后把BC和DC加起来即为巷子的宽度.
【解答】解:如图所示:AB=米,∠ACB=60°,∠DCE=45°,AC=CE
则在直角三角形ABC
,
∴,,
∴直角三角形DCE中,CE=AC=4,
∴,
∴,
∴
故答案为:
【点评】本题需要综合应用正切、正弦.余弦来求解,注意梯子长度不变,属于中档题.
18.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
【分析】可利用勾股定理及所给的比值得到所求的线段长.
【解答】解:∵AB=10米,tanA==.
∴设BC=x,AC=2x,
由勾股定理得,AB2=AC2+BC2,即100=x2+4x2,解得x=2,
∴AC=4,BC=2米.
故答案为4.
【点评】此题主要考查学生对坡度、坡角的掌握情况.
三.解答题(共8小题)
19.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
【分析】根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边计算即可.
【解答】解:∵∠C=90°,AC=8,AB=10,
∴BC==6,
则sinB==,
cosB==,
tanB==.
【点评】本题考查锐角三角函数的定义及运用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
20.在Rt△ABC中,∠ACB=90°
(1)tanA与sinA,cosA之间有什么关系?并说明理由.
(2)若=,求tanA的值.
【分析】(1)根据锐角三角函数的定义,分别表示出tanA与sinA,cosA的值,然后找出其中的关系即可;
(2)分式的分子和分母同时除以cos2A,然后解关于tanA的方程即可.
【解答】解:(1)∵tanA=,sinA=,cosA=,
∴tanA=.
(2)分式的分子、分母同时除以cos2A得:.
整理得:3tan2A﹣5tanA﹣2=0.
解得:tanA=2,或tanA=﹣(舍去).
∴tanA的值为2.
【点评】本题主要考查的是同角三角函数的关系,由三角函数的定义求得tanA=,然后得到关于tanA的方程是解题的关键.
21.计算:tan30°cos60°+tan45°cos30°.
【分析】根据特殊角的三角函数值可以计算出tan30°cos60°+tan45°cos30°的值.
【解答】解:tan30°cos60°+tan45°cos30°
=
=
=.
【点评】本题考查特殊角的三角函数值,解题的关键是明确特殊角的三角函数值.
22.已知三角函数值,求锐角(精确到1″).
(1)已知sinα=0.5018,求锐角α;
(2)已知tanθ=5,求锐角θ.
【分析】利用计算器进行计算即可,然后将结果化为度分秒的形式即可.
【解答】(1)∵sinα=0.5018,
∴α≈30.1191°.
∴a≈30°7′9″;
(2)∵tanθ=5,
∴θ=78.6900°≈78°41′24″.
【点评】本题考查了计算器的用法,是基础题,熟练掌握计算器的使用方法是解题的关键.
23.如图,在△ABC中;AD⊥BC,AB=20,AC=15,CD=9
(1)求BD的长;
(2)求∠BAC的度数.
【分析】(1)由垂直的定义得出∠ADB=∠ADC=90°,由勾股定理得出AD==12,中由勾股定理得出BD==16;
(2)由(1)得:BD=16,得出BC=BD+CD=25,证出AB2+AC2=BC2,由勾股定理的逆定理即可得出△ABC是直角三角形,∠BAC=90°.
【解答】解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD===12,
∴BD===16;
(2)由(1)得:BD=16,
∴BC=BD+CD=16+9=25,
∵AB=20,AC=15,
∴AB2+AC2=202+152=625,BC2=625,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°.
【点评】本题考查了勾股定理的逆定理和勾股定理的应用,熟练掌握勾股定理是解题的关键.
24.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【分析】过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AE?sin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
【解答】解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.3米,
∴EH=AE?sin∠EAH≈1.3×0.60=0.78(米),
∵AB=1.3米,
∴AB+EH≈1.3+0.78=2.08≈2.1(米);
答:适合该地下车库的车辆限高标志牌约为2.1米.
【点评】本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.
25.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.
【分析】过A点作AE⊥BC于点E,过D作DF⊥BC于点F,得到四边形AEFD是矩形,根据矩形的性质得到AE=DF=6,AD=EF=3,解直角三角形即可得到结论.
【解答】解:过A点作AE⊥BC于点E,过D作DF⊥BC于点F,
则四边形AEFD是矩形,有AE=DF=6,AD=EF=3,
∵坡角α=45°,β=30°,
∴BE=AE=6,CF=DF=6,
∴BC=BE+EF+CF=6+3+6=9+6,
∴BC=(9+6)m,
答:BC的长(9+6)m.
【点评】本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形和矩形,利用锐角三角函数的概念和坡度的概念求解.
26.2018年9月12日,临沂第六界中国百里沂河水上运动拉开帷幕,临沂电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为150米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)
【分析】由题意得:∠ADC=90°,CE∥AD,由平行线的性质得出∠BCD=45°,∠A=30°,由直角三角形的性质得出BD=CD=150米,AD=CD=150,即可得出答案.
【解答】解:由题意得:∠ADC=90°,CE∥AD,
∴∠BCD=45°,∠A=30°,
∴△BCD是等腰直角三角形,BD=CD=150米,AD=CD=150,
∴AB=AD﹣BD=150﹣150(米);
答:A、B两点间的距离为(150﹣150)米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题;通过解直角三角形求出AD和BD是解题的关键.
一.选择题(共10小题)
1.如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan∠AEB的值等于( )
A.3 B.2 C. D.
2.已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2﹣3x+1=0的两根,则△ABC是( )
A.锐角三角形
B.直角三角形或钝角三角形
C.钝角三角形
D.等边三角形
3.已知<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80° B.10°<α<80° C.60°<α<80° D.10°<α<60°
4.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
5.α为锐角,若sinα+cosα=,则sinα﹣cosα的值为( )
A. B.± C. D.0
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
7.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
8.在△ABC中,若||=0,且∠B,∠C都是锐角,则∠A的度数是( )
A.15° B.60° C.75° D.30°
9.将一副三角板如图摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值等于( )
A. B. C. D.
10.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
二.填空题(共8小题)
11.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值为 .
12.已知tanα=,那么sinα= .(其中α为锐角)
13.若tanα?tan50°=1,则锐角α= 度.
14.计算:(﹣)2﹣2cos60°= ;
15.先用计算器求:cos20°≈ ,cos40°≈ ,cos60°≈ ,cos80°≈ ,再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,cos80°连接起来: .归纳:余弦值,角大值 .
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
17.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为 米(结果保留根号).
18.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
三.解答题(共8小题)
19.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
20.在Rt△ABC中,∠ACB=90°
(1)tanA与sinA,cosA之间有什么关系?并说明理由.
(2)若=,求tanA的值.
21.计算:tan30°cos60°+tan45°cos30°.
22.已知三角函数值,求锐角(精确到1″).
(1)已知sinα=0.5018,求锐角α;
(2)已知tanθ=5,求锐角θ.
23.如图,在△ABC中;AD⊥BC,AB=20,AC=15,CD=9
(1)求BD的长;
(2)求∠BAC的度数.
24.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
25.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.
26.2018年9月12日,临沂第六界中国百里沂河水上运动拉开帷幕,临沂电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为150米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)
2019年沪科版九年级上册数学《第23章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan∠AEB的值等于( )
A.3 B.2 C. D.
【分析】过B作DC的平行线交DA的延长线于M,在DM的延长线上取MN=CE.
根据全等三角形及直角三角形的性质求出∠BNM两直角边的比,即可解答.
【解答】解:过B作DC的平行线交DA的延长线于M,在DM的延长线上取MN=CE.
则四边形MDCB为正方形,易得△MNB≌△CEB,
∴BE=BN.∴∠NBE=90°.
∵∠ABE=45°,∴∠ABE=∠ABN,
∴△NAB≌△EAB.
设EC=MN=x,AD=a,则AM=a,DE=2a﹣x,AE=AN=a+x,
∵AD2+DE2=AE2,
∴a2+(2a﹣x)2=(a+x)2,
∴x=a.
∴tan∠AEB=tan∠BNM==3.
故选:A.
【点评】本题考查的是锐角三角函数的定义,解答此题的关键是作出辅助线,构造出直角三角形,利用数形结合解答.
2.已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2﹣3x+1=0的两根,则△ABC是( )
A.锐角三角形
B.直角三角形或钝角三角形
C.钝角三角形
D.等边三角形
【分析】先解出方程的两根,讨论sinα,tanβ的值.∵在三角形中,角的范围是(0,180°),∴sinα必大于0,此时只要考虑tanβ的值即可,若tanβ>0,则β为锐角;tanβ小于0,则β为钝角.再把x的两个值分别代入sinα,tanβ中,可求出α,β的值,从而判断△ABC的形状.
【解答】解:由2x2﹣3x+1=0得:(2x﹣1)(x﹣1)=0,∴x=或x=1.
∴sinα>0,tanβ>0
若sinα=,tanβ=1,则α=30°,β=45°,γ=180°﹣30°﹣45°=105°,
∴△ABC为钝角三角形.
若sinα=1,tanβ=,则α=90°,β<90°,△ABC为直角三角形.
故选:B.
【点评】本题易在α,β上的取值出错,学生常常解出方程的两根后不知道如何判断,因此在解答时我们可对x的值分类讨论,从而判断出△ABC的形状.
3.已知<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80° B.10°<α<80° C.60°<α<80° D.10°<α<60°
【分析】由cos60°=,sin80°=cos10°,锐角α的余弦值随着α的变大而减小,可得出α的范围,从而可得答案.
【解答】解:∵cos60°=,<cosα<sin80°
锐角α的余弦值随着α的变大而减小,
故α<60°
∵sin80°=cos10°
∴10°<α<60°
故选:D.
【点评】本题考查了锐角三角函数的增减变化,明确锐角三角函数的增减变化以及特殊角的三角函数值,是解题的关键.
4.若0°<∠A<45°,那么sinA﹣cosA的值( )
A.大于0 B.小于0 C.等于0 D.不能确定
【分析】cosA=sin(90°﹣A),再根据余弦函数随角增大而减小进行分析.
【解答】解:∵cosA=sin(90°﹣A),余弦函数随角增大而减小,
∴当0°<∠A<45°时,sinA<cosA,即sinA﹣cosA<0.
故选:B.
【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.
5.α为锐角,若sinα+cosα=,则sinα﹣cosα的值为( )
A. B.± C. D.0
【分析】将两式分别两边平方,利用sin2α+cos2α=1,求出sinαcosα的值,解答即可.
【解答】解:∵sinα+cosα=,
∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0.
∴sinα﹣cosα=0.
故选:D.
【点评】本题利用了同角的三角函数的关系sin2α+cos2α=1来进行化简求值的.
6.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
【分析】本题可根据非负数的性质“两个非负数相加和为0,这两个非负数的值都为0.”分别求出∠A、∠B的值.然后用三角形内角和定理即可求出∠C的值.
【解答】解:∵|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,=cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选:C.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握二次根式、绝对值、非负数等考点的运算.
7.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )
A.45° B.75° C.105° D.120°
【分析】根据非负数的性质列出关系式,根据特殊角的三角函数值求出∠A、∠B的度数,根据三角形内角和定理计算即可.
【解答】解:由题意得,sinA﹣=0,﹣cosB=0,
即sinA=,=cosB,
解得,∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°,
故选:C.
【点评】本题考查的是非负数的性质的应用、特殊角的三角函数值的计算和三角形内角和定理的应用,熟记特殊角的三角函数值是解题的关键.
8.在△ABC中,若||=0,且∠B,∠C都是锐角,则∠A的度数是( )
A.15° B.60° C.75° D.30°
【分析】先根据非负数的性质求出sinB及cosC的值,再由特殊角的三角函数值解答即可.
【解答】解:∵ +|﹣cosC|=0,
∴sinB﹣=0;﹣cosC=0.
即sinB=;cosC=.
∴∠B=45°,∠C=60°.
∴∠A=180°﹣∠B﹣∠C=180°﹣45°﹣60°=75°.
故选:C.
【点评】此题涉及到非负数的性质、特殊角的三角函数值及三角形内角和定理.
9.将一副三角板如图摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值等于( )
A. B. C. D.
【分析】如图所示,连接BD,过点D作DE垂直于BC的延长线于点E,构造直角三角形,将∠CBD置于直角三角形中,设CE为1,根据特殊直角三角形分别求得线段CD、AC、BC,从而按正切函数的定义可解.
【解答】解:如图所示,连接BD,过点D作DE垂直于BC的延长线于点E
∵在Rt△ABC中,∠ACB=45°,在Rt△ACD中,∠ACD=90°
∴∠DCE=45°,
∵DE⊥CE
∴∠CED=90°,∠CDE=45°
∴设DE=CE=1,则CD=
在Rt△ACD中,
∵∠CAD=30°,
∴tan∠CAD=,则AC=,
在Rt△ABC中,∠BAC=∠BCA=45°
∴BC=,
∴在Rt△BED中,tan∠CBD===
故选:D.
【点评】本题考查了用定义求三角函数,同时考查了特殊角的三角函数值,如何作辅助线,是解题的关键.
10.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
【分析】证明△ABC∽△DAB,得出=,证出AD=2BC,得出AB2=BC×AD=BC×2BC=2BC2,因此AB=BC,在Rt△ABC中,由三角函数定义即可得出答案.
【解答】解:∵AD∥BC,∠DAB=90°,
∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB+∠EAD=90°,
∴∠BAC=∠ADB,
∴△ABC∽△DAB,
∴=,
∵BC=AD,
∴AD=2BC,
∴AB2=BC×AD=BC×2BC=2BC2,
∴AB=BC,
在Rt△ABC中,tan∠BAC===;
故选:C.
【点评】本题考查了平行线的性质、相似三角形的判定与性质以及解直角三角形的应用等知识;熟练掌握解直角三角形,证明三角形相似是解题的关键.
二.填空题(共8小题)
11.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值为 3 .
【分析】根据点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,可以求得t的值.
【解答】解:∵点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,
∴tanα==.
解得t=3.
故答案为:3.
【点评】本题考查锐角三角函数,解题的关键是明确锐角三角函数的定义和第一象限点的特点.
12.已知tanα=,那么sinα= .(其中α为锐角)
【分析】根据锐角三角函数的定义,设∠A=α,放在直角三角形ACB中,设BC=4x,AC=3x,由勾股定理求出AB,再根据锐角三角函数的定义求出即可.
【解答】解:
∵∠C=90°,∠A=α,
∵tanα==,
设BC=4x,AC=3x,
由勾股定理得:AB==5x,
∴sinα=sin∠A===.
故答案为:.
【点评】本题考查了勾股定理,锐角三角函数等知识点,解此题的关键是把所求角放在直角三角形中,思路是根据锐角三角函数的定义和直角三角形求出即可.题目较好,难度不大.
13.若tanα?tan50°=1,则锐角α= 40 度.
【分析】根据锐角三角函数的定义得出如果tanα?tan50°=1,那么α+50°=90°,即可求出答案.
【解答】解:∵在△ACB中∠C=90°,∠A=α,∠B=50°,
∵tanA=,tanB=,
∴tanA?tanB=×=1,
∴∠A+∠B=90°,
∵tanα?tan50°=1,
∴α=90°﹣50°=40°.
故答案为:40.
【点评】本题主要考查对互余两角的三角函数的关系,锐角三角函数的定义等知识点的理解和掌握,能熟练地运用性质进行计算是解此题的关键.
14.计算:(﹣)2﹣2cos60°= ﹣ ;
【分析】先算平方,特殊角的三角函数值,再算减法即可求解.
【解答】解:(﹣)2﹣2cos60°
=﹣2×
=﹣1
=﹣.
故答案为:﹣.
【点评】考查了特殊角的三角函数值,关键是熟练掌握60°的余弦值.
15.先用计算器求:cos20°≈ 0.9397 ,cos40°≈ 0.7660 ,cos60°≈ 0.5 ,cos80°≈ 0.1736 ,再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,cos80°连接起来: cos20°>cos40°>cos60°>cos80° .归纳:余弦值,角大值 小 .
【分析】利用计算器分别计算各个三角函数值,然后根据角的增大,来观察余弦数值的变化.
【解答】解:利用计算器可算出:cos20°≈0.9397,cos40°≈0.7660,cos60°=0.5,cos80°≈0.1736,
∴cos20°>cos40°>cos60°>cos80°
∴在锐角范围内,余弦函数值随着角度的增大而减小,即余弦值,角大值小.
故答案是0.9397,0.7660,0.5,0.1736,小.
【点评】本题考查了计算器求三角函数值,注意小数点后保留3位或4位有效数字.
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
【分析】先由AF平分∠CAB,CD⊥AB,过点E作EG垂直于AC,利用角平分线的性质定理得EG等于DE,易得Rt△AED全等于Rt△AEG以及∠DCA等于∠B,从而求得AD,AG,CG,然后在Rt△CEG中,由勾股定理求出EG,即为DE的长度.
【解答】解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
【点评】本题综合运用了角平分线的性质定理,全等三角形判断,勾股定理等知识,难度较大.
17.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为 2+2 米(结果保留根号).
【分析】本题需要分段求出巷子被分成的两部分,再加起来即可.先在直角三角形ABC中,用正切和正弦,分别求出BC和AC(即梯子的长度),然后再在直角三角形DCE中,用∠DCE的余弦求出DC,然后把BC和DC加起来即为巷子的宽度.
【解答】解:如图所示:AB=米,∠ACB=60°,∠DCE=45°,AC=CE
则在直角三角形ABC
,
∴,,
∴直角三角形DCE中,CE=AC=4,
∴,
∴,
∴
故答案为:
【点评】本题需要综合应用正切、正弦.余弦来求解,注意梯子长度不变,属于中档题.
18.如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离出发点的水平距离为 m.
【分析】可利用勾股定理及所给的比值得到所求的线段长.
【解答】解:∵AB=10米,tanA==.
∴设BC=x,AC=2x,
由勾股定理得,AB2=AC2+BC2,即100=x2+4x2,解得x=2,
∴AC=4,BC=2米.
故答案为4.
【点评】此题主要考查学生对坡度、坡角的掌握情况.
三.解答题(共8小题)
19.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
【分析】根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边计算即可.
【解答】解:∵∠C=90°,AC=8,AB=10,
∴BC==6,
则sinB==,
cosB==,
tanB==.
【点评】本题考查锐角三角函数的定义及运用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
20.在Rt△ABC中,∠ACB=90°
(1)tanA与sinA,cosA之间有什么关系?并说明理由.
(2)若=,求tanA的值.
【分析】(1)根据锐角三角函数的定义,分别表示出tanA与sinA,cosA的值,然后找出其中的关系即可;
(2)分式的分子和分母同时除以cos2A,然后解关于tanA的方程即可.
【解答】解:(1)∵tanA=,sinA=,cosA=,
∴tanA=.
(2)分式的分子、分母同时除以cos2A得:.
整理得:3tan2A﹣5tanA﹣2=0.
解得:tanA=2,或tanA=﹣(舍去).
∴tanA的值为2.
【点评】本题主要考查的是同角三角函数的关系,由三角函数的定义求得tanA=,然后得到关于tanA的方程是解题的关键.
21.计算:tan30°cos60°+tan45°cos30°.
【分析】根据特殊角的三角函数值可以计算出tan30°cos60°+tan45°cos30°的值.
【解答】解:tan30°cos60°+tan45°cos30°
=
=
=.
【点评】本题考查特殊角的三角函数值,解题的关键是明确特殊角的三角函数值.
22.已知三角函数值,求锐角(精确到1″).
(1)已知sinα=0.5018,求锐角α;
(2)已知tanθ=5,求锐角θ.
【分析】利用计算器进行计算即可,然后将结果化为度分秒的形式即可.
【解答】(1)∵sinα=0.5018,
∴α≈30.1191°.
∴a≈30°7′9″;
(2)∵tanθ=5,
∴θ=78.6900°≈78°41′24″.
【点评】本题考查了计算器的用法,是基础题,熟练掌握计算器的使用方法是解题的关键.
23.如图,在△ABC中;AD⊥BC,AB=20,AC=15,CD=9
(1)求BD的长;
(2)求∠BAC的度数.
【分析】(1)由垂直的定义得出∠ADB=∠ADC=90°,由勾股定理得出AD==12,中由勾股定理得出BD==16;
(2)由(1)得:BD=16,得出BC=BD+CD=25,证出AB2+AC2=BC2,由勾股定理的逆定理即可得出△ABC是直角三角形,∠BAC=90°.
【解答】解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD===12,
∴BD===16;
(2)由(1)得:BD=16,
∴BC=BD+CD=16+9=25,
∵AB=20,AC=15,
∴AB2+AC2=202+152=625,BC2=625,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°.
【点评】本题考查了勾股定理的逆定理和勾股定理的应用,熟练掌握勾股定理是解题的关键.
24.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【分析】过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AE?sin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
【解答】解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF﹣∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.3米,
∴EH=AE?sin∠EAH≈1.3×0.60=0.78(米),
∵AB=1.3米,
∴AB+EH≈1.3+0.78=2.08≈2.1(米);
答:适合该地下车库的车辆限高标志牌约为2.1米.
【点评】本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.
25.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.
【分析】过A点作AE⊥BC于点E,过D作DF⊥BC于点F,得到四边形AEFD是矩形,根据矩形的性质得到AE=DF=6,AD=EF=3,解直角三角形即可得到结论.
【解答】解:过A点作AE⊥BC于点E,过D作DF⊥BC于点F,
则四边形AEFD是矩形,有AE=DF=6,AD=EF=3,
∵坡角α=45°,β=30°,
∴BE=AE=6,CF=DF=6,
∴BC=BE+EF+CF=6+3+6=9+6,
∴BC=(9+6)m,
答:BC的长(9+6)m.
【点评】本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形和矩形,利用锐角三角函数的概念和坡度的概念求解.
26.2018年9月12日,临沂第六界中国百里沂河水上运动拉开帷幕,临沂电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为150米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)
【分析】由题意得:∠ADC=90°,CE∥AD,由平行线的性质得出∠BCD=45°,∠A=30°,由直角三角形的性质得出BD=CD=150米,AD=CD=150,即可得出答案.
【解答】解:由题意得:∠ADC=90°,CE∥AD,
∴∠BCD=45°,∠A=30°,
∴△BCD是等腰直角三角形,BD=CD=150米,AD=CD=150,
∴AB=AD﹣BD=150﹣150(米);
答:A、B两点间的距离为(150﹣150)米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题;通过解直角三角形求出AD和BD是解题的关键.
