2019秋湘教版九年级数学上册第一章反比例函数周测 :1.2 反比例函数的图像与性质 同步练习(含答案)
文档属性
| 名称 | 2019秋湘教版九年级数学上册第一章反比例函数周测 :1.2 反比例函数的图像与性质 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览


文档简介
2019秋湘教版九年级数学上册第一章反比例函数周测1.2学案设计
一、选择题(共30分)
1.反比例函数y=的图象分布在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
2.在反比例函数y=(k<0)的图象上有两点(-1,y1),(-,y2),则y1-y2的值是( )
A.负数 B.非正数 C.正数 D.不能确定
3.已知点A(x1,y1),B(x2,y2)是反比例函数y=的图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C. y1<y2<0 D.y2<y1<0
4.若点A(1,y1)、B(2,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系为( )
A. y1<y2 B. y1≤y2 C. y1>y2 D. y1≥y2
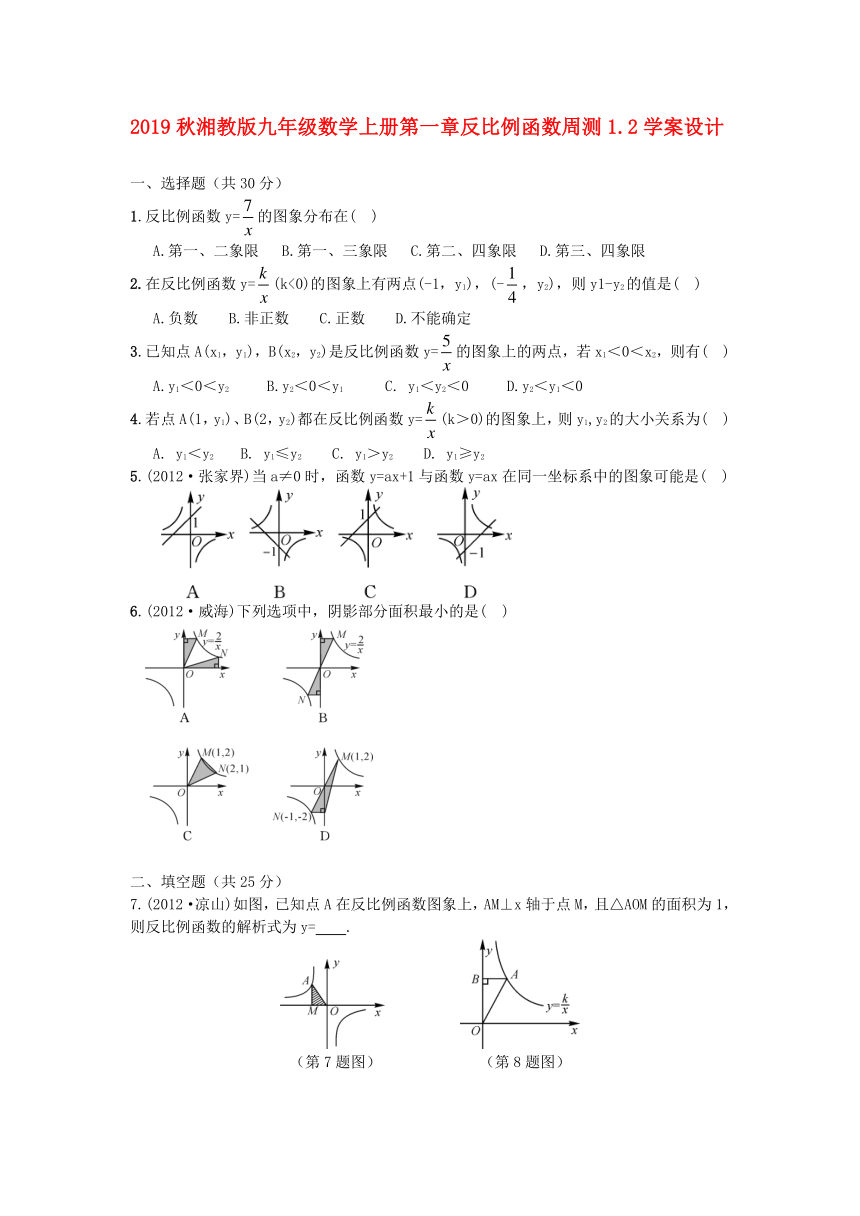
5.(2012·张家界)当a≠0时,函数y=ax+1与函数y=ax在同一坐标系中的图象可能是( )
6.(2012·威海)下列选项中,阴影部分面积最小的是( )
二、填空题(共25分)
7.(2012·凉山)如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为y= .
(第7题图) (第8题图)
8.(2013·娄底)如图,已知A点是反比例函数y=(k≠0)的图象上一点, AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
9.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
(第9题图) (第10题图)
10.如图,直线x=2与反比例函数y=和y=-的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
11.若点A(-2,-2)在反比例函数y=的图象上,则当函数值y≥-2时,自变量x的取值范围是 .
三、解答题(共45分)
12.(10分)如图,已知反比例函数y=(k≠0)的图象经过点A(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
13.(10分)已知:如图,双曲线y=的图象经过A(1,2)、B(2,b)两点.
(1)求双曲线的解析式;
(2)试比较b与2的大小.
14.(12分)如图,一次函数y1=x+1的图象与反比例函数y2=(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求A点的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1与y2的大小.
15.(13分)如图,已知双曲线y=和直线y=mx+n交于点A和点B,B点的坐标是
(2,-3),AC垂直y轴于点C,AC=.
(1)求双曲线和直线的解析式;
(2)求△AOB的面积.
参考答案
1.B 2.A 1.A 2. C 10.C 11.C
7. - 8. 6 9. 1 10.1.5 11.x≤-2或x>0
12.(1)y=-.
(2)y1<y2.理由:
∵k=-16<0,在每一象限内,函数值y随x的增大而增大,而点(2,y1),(4,y2)都在第四象限,且2<4,∴y1<y2.
13.(1)双曲线的解析式为y=.
(2)由函数y=的性质可得在第一象限y随x的增大而减小,因为2>1,所以b<2.
14.(1)∵一次函数y1=x+1的图象经过点A(m,2),∴2=m+1.解得m=1.
∴点A的坐标为A(1,2).
∵反比例函数y2=的图象经过点A(1,2),∴2=.解得k=2.
∴反比例函数的表达式为y2=.
(2)由图象得:当0<x<1时,y1<y2;当x=1时,y1=y2;当x>1时,y1>y2.
15.(1)双曲线的解析式为y=-,直线的解析式为y=-2x+1.
(2)设直线与x轴的交点为D.易求得点D的坐标为(,0),∴OD=.
∴S△AOB=S△AOD+S△BOD=××4+××3=.
一、选择题(共30分)
1.反比例函数y=的图象分布在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
2.在反比例函数y=(k<0)的图象上有两点(-1,y1),(-,y2),则y1-y2的值是( )
A.负数 B.非正数 C.正数 D.不能确定
3.已知点A(x1,y1),B(x2,y2)是反比例函数y=的图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C. y1<y2<0 D.y2<y1<0
4.若点A(1,y1)、B(2,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系为( )
A. y1<y2 B. y1≤y2 C. y1>y2 D. y1≥y2
5.(2012·张家界)当a≠0时,函数y=ax+1与函数y=ax在同一坐标系中的图象可能是( )
6.(2012·威海)下列选项中,阴影部分面积最小的是( )
二、填空题(共25分)
7.(2012·凉山)如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为1,则反比例函数的解析式为y= .
(第7题图) (第8题图)
8.(2013·娄底)如图,已知A点是反比例函数y=(k≠0)的图象上一点, AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
9.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
(第9题图) (第10题图)
10.如图,直线x=2与反比例函数y=和y=-的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
11.若点A(-2,-2)在反比例函数y=的图象上,则当函数值y≥-2时,自变量x的取值范围是 .
三、解答题(共45分)
12.(10分)如图,已知反比例函数y=(k≠0)的图象经过点A(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1,y2的大小,并说明理由.
13.(10分)已知:如图,双曲线y=的图象经过A(1,2)、B(2,b)两点.
(1)求双曲线的解析式;
(2)试比较b与2的大小.
14.(12分)如图,一次函数y1=x+1的图象与反比例函数y2=(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求A点的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1与y2的大小.
15.(13分)如图,已知双曲线y=和直线y=mx+n交于点A和点B,B点的坐标是
(2,-3),AC垂直y轴于点C,AC=.
(1)求双曲线和直线的解析式;
(2)求△AOB的面积.
参考答案
1.B 2.A 1.A 2. C 10.C 11.C
7. - 8. 6 9. 1 10.1.5 11.x≤-2或x>0
12.(1)y=-.
(2)y1<y2.理由:
∵k=-16<0,在每一象限内,函数值y随x的增大而增大,而点(2,y1),(4,y2)都在第四象限,且2<4,∴y1<y2.
13.(1)双曲线的解析式为y=.
(2)由函数y=的性质可得在第一象限y随x的增大而减小,因为2>1,所以b<2.
14.(1)∵一次函数y1=x+1的图象经过点A(m,2),∴2=m+1.解得m=1.
∴点A的坐标为A(1,2).
∵反比例函数y2=的图象经过点A(1,2),∴2=.解得k=2.
∴反比例函数的表达式为y2=.
(2)由图象得:当0<x<1时,y1<y2;当x=1时,y1=y2;当x>1时,y1>y2.
15.(1)双曲线的解析式为y=-,直线的解析式为y=-2x+1.
(2)设直线与x轴的交点为D.易求得点D的坐标为(,0),∴OD=.
∴S△AOB=S△AOD+S△BOD=××4+××3=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
