2019秋湘教版九年级数学上册第3章 相似三角形中的基本模型 专题试卷(含答案)
文档属性
| 名称 | 2019秋湘教版九年级数学上册第3章 相似三角形中的基本模型 专题试卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 00:00:00 | ||
图片预览


文档简介
2019秋湘教版九年级数学上册模型构建专题相似三角形中的基本模型
类型一 “A”字型
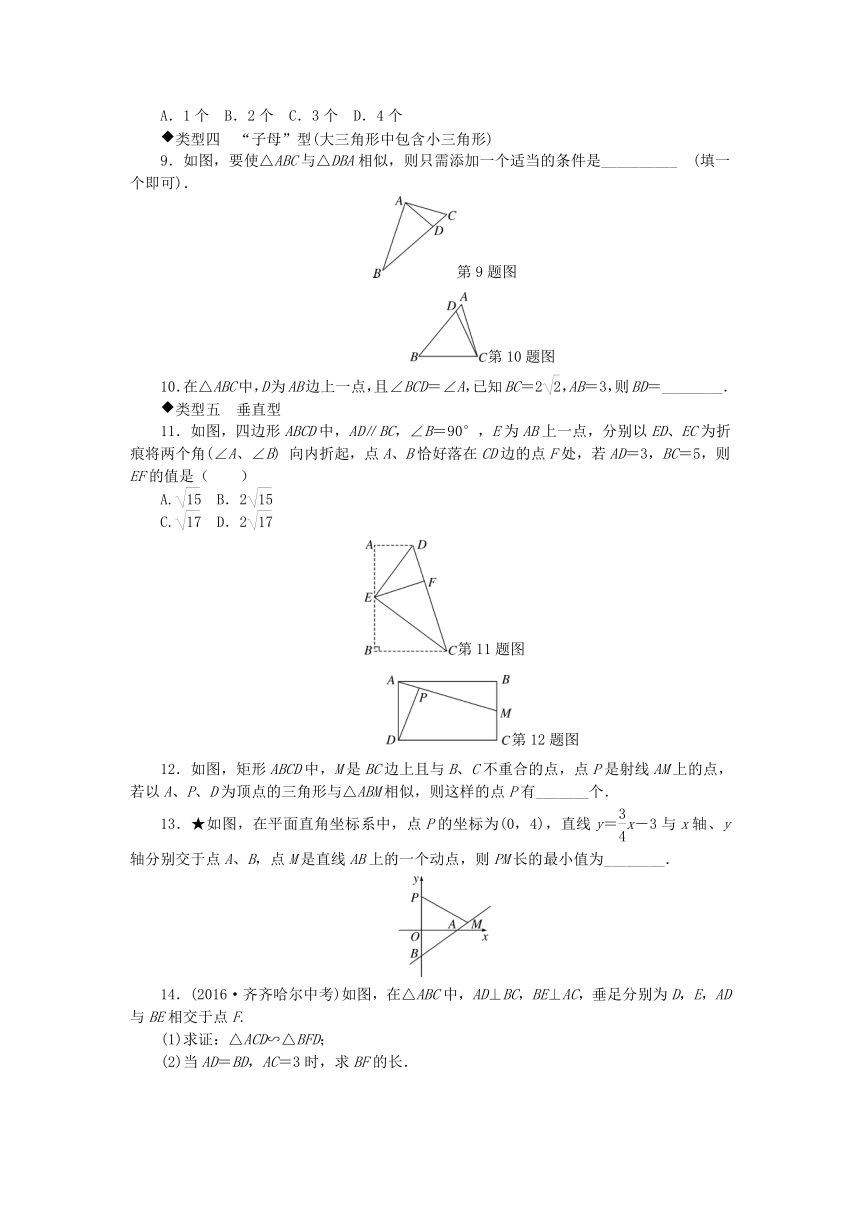
1.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=3,DB=2,BC=6,则DE的长为________.
第1题图
第2题图
2.如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是________.
3.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于点M,交AD的延长线于点N,则+=________.
第3题图
4.如图①,已知AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC交于点E,EF⊥BD,垂足为F,我们可以证明+=成立.若将图①中的垂直改为斜交,如图②,AB∥CD,AD与BC交于点E,过点E作EF∥AB交BD于F,则+=还成立吗?如果成立,给出证明;如果不成立,请说明理由.
类型二 “X”字型
5.(2016·哈尔滨中考)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A.= B.=
C.= D.=
第5题图
第6题图
6.如图,?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF∶BD等于( )
A.2∶3 B.2∶1 C.1∶2 D.1∶3
7.如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2,=,求线段DC的长;
(2)求证:EF·GB=BF·GE.
类型三 旋转型
8.如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB′F相似的三角形有(不再添加其他线段)( )
A.1个 B.2个 C.3个 D.4个
类型四 “子母”型(大三角形中包含小三角形)
9.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是__________ (填一个即可).
第9题图
第10题图
10.在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD=________.
类型五 垂直型
11.如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A、∠B) 向内折起,点A、B恰好落在CD边的点F处,若AD=3,BC=5,则EF的值是( )
A. B.2
C. D.2
第11题图
第12题图
12.如图,矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点P有_______个.
13.★如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为________.
14.(2016·齐齐哈尔中考)如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当AD=BD,AC=3时,求BF的长.
类型六 一线三等角型
15.如图,等边△ABC的边长为6,D是BC边上的点,∠EDF=60°.若BD=1,CF=3时,则BE的长为________.【方法12】
第15题图
变式题图
【变式题】如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于________.
16.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.【方法12】
模型构建专题:相似三角形中的基本模型
1. 2.25
3.1 解析:∵AB=BC=CD=AD=1,BC∥AD,∴=,即=,∴+=+==1.
4.解:成立.证明如下:∵AB∥EF∥CD,∴△DEF∽△DAB,△BEF∽△BCD,∴=,=,两式相加,得+=+=1,等式两边同时除以EF,得+=.
5.A 6.D
7.(1)解:∵AD∥BC,∴△DEF∽△CBF,∴==,∴FC=3FD=6,∴DC=FC-FD=4;
(2)证明:∵AD∥BC,∴△DEF∽△CBF,△AEG∽△CBG,∴=,=.∵点E是边AD的中点,∴AE=DE,∴=,∴EF·GB=BF·GE.
8.D
9.∠BAC=∠BDA(答案不唯一)
10. 11.A 12.2
13. 解析:根据“垂线段最短”,得PM的最小值就是当PM⊥AB时PM的长.∵直线y=x-3与x轴、y轴分别交于点A、B,∴令x=0,得y=-3,∴点B的坐标为(0,-3),即OB=3.令y=0,得x=4,∴点A的坐标为(4,0), 即OA=4,∴PB=OP+OB=4+3=7.在Rt△AOB中,根据勾股定理得AB===5.在Rt△PMB与Rt△AOB中,∵∠PBM=∠ABO,∠PMB=∠AOB,∴Rt△PMB∽Rt△AOB,∴=,即=,解得PM=.
14.(1)证明:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,∴∠C+∠DBF=90°,∠C+∠DAC=90°,∴∠DBF=∠DAC,∴△ACD∽△BFD;
(2)解:∵AD=BD,△ACD∽△BFD,∴==1,∴BF=AC=3.
15. 解析:∵△ABC为等边三角形,∴∠B=∠C=60°.∵∠EDF=60°,∴∠BED+∠EDB=∠EDB+∠FDC=120°,∴∠BED=∠FDC,∴△BDE∽△CFD,∴=.∵BC=6,BD=1,∴CD=BC-BD=5,∴=,解得BE=.
【变式题】 2 解析:∵△ABC和△ADE均为等边三角形,∴∠B=∠C=∠ADE=60°.∵∠ADC=∠ADE+∠FDC=∠B+∠BAD,∴∠BAD=∠CDF,∴△BAD∽△CDF,∴AB∶BD=CD∶CF,即9∶3=(9-3)∶CF,∴CF=2.
16.(1)证明:∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,∴AB·CD=CP·BP,∴AC·CD=CP·BP;
(2)解:∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.又∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=.
类型一 “A”字型
1.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=3,DB=2,BC=6,则DE的长为________.
第1题图
第2题图
2.如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是________.
3.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于点M,交AD的延长线于点N,则+=________.
第3题图
4.如图①,已知AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC交于点E,EF⊥BD,垂足为F,我们可以证明+=成立.若将图①中的垂直改为斜交,如图②,AB∥CD,AD与BC交于点E,过点E作EF∥AB交BD于F,则+=还成立吗?如果成立,给出证明;如果不成立,请说明理由.
类型二 “X”字型
5.(2016·哈尔滨中考)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A.= B.=
C.= D.=
第5题图
第6题图
6.如图,?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF∶BD等于( )
A.2∶3 B.2∶1 C.1∶2 D.1∶3
7.如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2,=,求线段DC的长;
(2)求证:EF·GB=BF·GE.
类型三 旋转型
8.如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB′F相似的三角形有(不再添加其他线段)( )
A.1个 B.2个 C.3个 D.4个
类型四 “子母”型(大三角形中包含小三角形)
9.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是__________ (填一个即可).
第9题图
第10题图
10.在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD=________.
类型五 垂直型
11.如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A、∠B) 向内折起,点A、B恰好落在CD边的点F处,若AD=3,BC=5,则EF的值是( )
A. B.2
C. D.2
第11题图
第12题图
12.如图,矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点P有_______个.
13.★如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为________.
14.(2016·齐齐哈尔中考)如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当AD=BD,AC=3时,求BF的长.
类型六 一线三等角型
15.如图,等边△ABC的边长为6,D是BC边上的点,∠EDF=60°.若BD=1,CF=3时,则BE的长为________.【方法12】
第15题图
变式题图
【变式题】如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于________.
16.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.【方法12】
模型构建专题:相似三角形中的基本模型
1. 2.25
3.1 解析:∵AB=BC=CD=AD=1,BC∥AD,∴=,即=,∴+=+==1.
4.解:成立.证明如下:∵AB∥EF∥CD,∴△DEF∽△DAB,△BEF∽△BCD,∴=,=,两式相加,得+=+=1,等式两边同时除以EF,得+=.
5.A 6.D
7.(1)解:∵AD∥BC,∴△DEF∽△CBF,∴==,∴FC=3FD=6,∴DC=FC-FD=4;
(2)证明:∵AD∥BC,∴△DEF∽△CBF,△AEG∽△CBG,∴=,=.∵点E是边AD的中点,∴AE=DE,∴=,∴EF·GB=BF·GE.
8.D
9.∠BAC=∠BDA(答案不唯一)
10. 11.A 12.2
13. 解析:根据“垂线段最短”,得PM的最小值就是当PM⊥AB时PM的长.∵直线y=x-3与x轴、y轴分别交于点A、B,∴令x=0,得y=-3,∴点B的坐标为(0,-3),即OB=3.令y=0,得x=4,∴点A的坐标为(4,0), 即OA=4,∴PB=OP+OB=4+3=7.在Rt△AOB中,根据勾股定理得AB===5.在Rt△PMB与Rt△AOB中,∵∠PBM=∠ABO,∠PMB=∠AOB,∴Rt△PMB∽Rt△AOB,∴=,即=,解得PM=.
14.(1)证明:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,∴∠C+∠DBF=90°,∠C+∠DAC=90°,∴∠DBF=∠DAC,∴△ACD∽△BFD;
(2)解:∵AD=BD,△ACD∽△BFD,∴==1,∴BF=AC=3.
15. 解析:∵△ABC为等边三角形,∴∠B=∠C=60°.∵∠EDF=60°,∴∠BED+∠EDB=∠EDB+∠FDC=120°,∴∠BED=∠FDC,∴△BDE∽△CFD,∴=.∵BC=6,BD=1,∴CD=BC-BD=5,∴=,解得BE=.
【变式题】 2 解析:∵△ABC和△ADE均为等边三角形,∴∠B=∠C=∠ADE=60°.∵∠ADC=∠ADE+∠FDC=∠B+∠BAD,∴∠BAD=∠CDF,∴△BAD∽△CDF,∴AB∶BD=CD∶CF,即9∶3=(9-3)∶CF,∴CF=2.
16.(1)证明:∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,∴AB·CD=CP·BP,∴AC·CD=CP·BP;
(2)解:∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.又∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
