11.3.2 多边形的内角和课件(29张ppt)
文档属性
| 名称 | 11.3.2 多边形的内角和课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 20:12:00 | ||
图片预览







文档简介
(共29张PPT)
人教版数学教材八年级上
11.3多边形及其内角和(2)
你能算它的内角和吗?
它们的内角和该怎么计算呢?
其他多边形的内角和呢?
想一想
你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
让我们从简单的多边形的内角和开始探索!
Why?
A
B
C
D
在探究四边形的内角和时,有的同学不是用量角器度量、计算得到,而是 按照如图所示,利用辅助线将四边形分割成两个三角形的方法,利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?并且能否启发你借助辅助线找到解决其他多边形的方法吗?
四边形内角和
那么如何求此五边形的内角和呢?
选捷径,我能行!
3× 180° =5400
说说你的 探索思路?
—从一个顶点出发添两条对角线,目的是把五边形分割成三个三角形,再利用三角形的内角和求得。
A
B
C
D
E
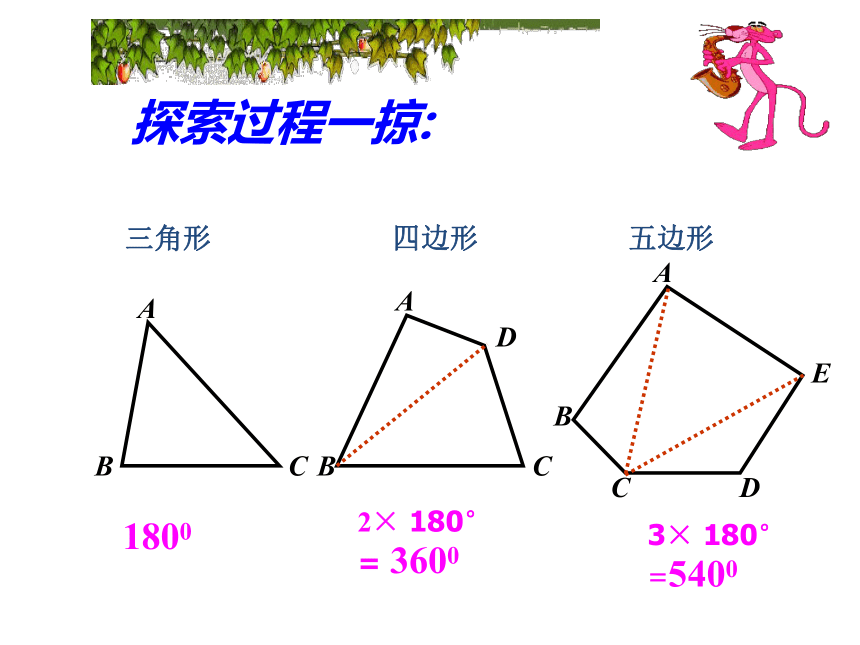
三角形
四边形
五边形
1800
2× 180°
= 3600
3× 180° =5400
探索过程一掠:
A
C
B
A
B
C
D
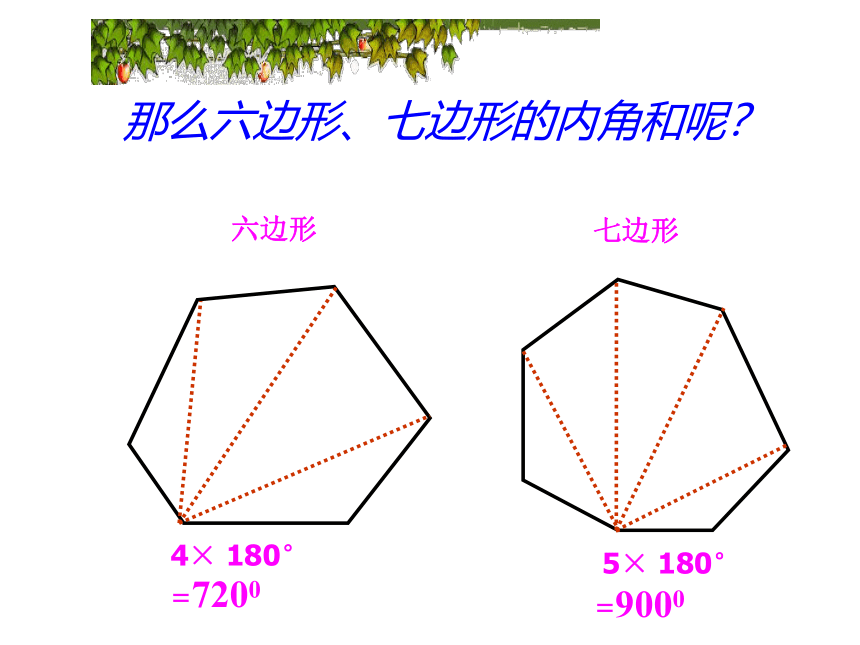
六边形
七边形
4× 180° =7200
5× 180° =9000
那么六边形、七边形的内角和呢?
学一学
四边形的内角和 (4-2)× 180° = 360°
五边形的内角和 (5-2)× 180°=540°
六边形的内角和(6-2)× 180°=720°
七边形的内角(7-2)×180°=900°
这种探索方法你掌握了吗?请完成下表
边数 3 4 5 6 7 …
三角形个数 1 2 …
内角和 1×1800 2×1800 …
n-2
3×1800
4×1800
5×1800
(n-2)x1800
n
A3
A8
An
A1
A2
A7
A5
A6
A4
试一试
找规律
3
4
5
说明: 从n边形的一个顶点出发可以引 条对角线,这些对角线把n边形分成 个三角形,内角和为 .
(n-3)
(n-2)
(n-2)x180°
探索多边形的内角和
P
A
B
C
D
图 1
P
A
B
D
C
图 2
P
A
B
C
D
图 3
P
A
B
C
D
图 1
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
P
A
B
C
D
图 3
如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°
百家争鸣
其他方法
其他方案
我们也可以利用以上不同的方法分割多边形,得到n边形的内角和公式
p
p
p
照猫画虎
n边形内角和等于
最终结论
(n-2)× 180°
2、已知一个多边形每个内角都等108° ,求这个多边形的边数?
解:设这个多边形的边数为 n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。
1、八边形的内角和等于多少度? 十边形呢?
(8-2) ×180°= 1080°
(10-2) ×180°= 1440°
抢 答
解:如图四边形ABCD中,
A
B
C
D
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
典型例题
求下列图形中x的值:
∟
(1)
∟
(2)
(3)
C
A
B
D
E
(4)
AB∥CD
随堂练习
那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢?
……
正n边形
(5-2)×180°
5
=108°
(6-2)×180°
6
=120°
(8-2)×180°
8
=135°
(n-2)×180°
n
Now I can ……
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5=吗?你是怎样得到的?
(1)小明每从一条街道转到下一条街道时,身体转过的角是 哪 个 角?
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
D'
A'
C'
E'
B'
O
β
γ
δ
θ
α
A
B
C
D
E
1
2
3
4
5
结论:
?1, ? 2, ? 3, ? 4, ? 5的和等于360?
多边形 内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的外角和等于360?
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
多边形的外角和
A3
A8
An
A1
A2
A7
A5
A6
A4
各抒己见
多边形的外角和等于360?
多边形 外角与内角有何关系?还有其他方法可以推导出多边形外角和?
多边形的任何一个内角加上与它相邻的内角都等于180°(平角),n个外角连同它们的各自相邻的内角,共有n个180°,总和为n× 180° ,再用它减去n个内角的和,剩下的就是多边形的外角和了!
1.正五边形 的每一个外角等于___.每一个内角等于_____,
72°
144°
2.如果一个正多边形的一个内角等于120°,则这个多边 形的边 数是_____
6
3.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____
A.12 B.9 C. 8 D.7
A
3.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____
12
随堂练习
学习了本节课你有哪些 收获?
1. P24-25 2,3,5,6
7,8,9,10
2.阅读P26
作 业
课后思考
1、小明在计算某个多边形的内角和时,由于
粗心他漏掉一个内角,求得的内角和1680° ,你能否求得正确结果呢?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
人教版数学教材八年级上
11.3多边形及其内角和(2)
你能算它的内角和吗?
它们的内角和该怎么计算呢?
其他多边形的内角和呢?
想一想
你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
让我们从简单的多边形的内角和开始探索!
Why?
A
B
C
D
在探究四边形的内角和时,有的同学不是用量角器度量、计算得到,而是 按照如图所示,利用辅助线将四边形分割成两个三角形的方法,利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?并且能否启发你借助辅助线找到解决其他多边形的方法吗?
四边形内角和
那么如何求此五边形的内角和呢?
选捷径,我能行!
3× 180° =5400
说说你的 探索思路?
—从一个顶点出发添两条对角线,目的是把五边形分割成三个三角形,再利用三角形的内角和求得。
A
B
C
D
E
三角形
四边形
五边形
1800
2× 180°
= 3600
3× 180° =5400
探索过程一掠:
A
C
B
A
B
C
D
六边形
七边形
4× 180° =7200
5× 180° =9000
那么六边形、七边形的内角和呢?
学一学
四边形的内角和 (4-2)× 180° = 360°
五边形的内角和 (5-2)× 180°=540°
六边形的内角和(6-2)× 180°=720°
七边形的内角(7-2)×180°=900°
这种探索方法你掌握了吗?请完成下表
边数 3 4 5 6 7 …
三角形个数 1 2 …
内角和 1×1800 2×1800 …
n-2
3×1800
4×1800
5×1800
(n-2)x1800
n
A3
A8
An
A1
A2
A7
A5
A6
A4
试一试
找规律
3
4
5
说明: 从n边形的一个顶点出发可以引 条对角线,这些对角线把n边形分成 个三角形,内角和为 .
(n-3)
(n-2)
(n-2)x180°
探索多边形的内角和
P
A
B
C
D
图 1
P
A
B
D
C
图 2
P
A
B
C
D
图 3
P
A
B
C
D
图 1
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
P
A
B
C
D
图 3
如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°
百家争鸣
其他方法
其他方案
我们也可以利用以上不同的方法分割多边形,得到n边形的内角和公式
p
p
p
照猫画虎
n边形内角和等于
最终结论
(n-2)× 180°
2、已知一个多边形每个内角都等108° ,求这个多边形的边数?
解:设这个多边形的边数为 n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。
1、八边形的内角和等于多少度? 十边形呢?
(8-2) ×180°= 1080°
(10-2) ×180°= 1440°
抢 答
解:如图四边形ABCD中,
A
B
C
D
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
典型例题
求下列图形中x的值:
∟
(1)
∟
(2)
(3)
C
A
B
D
E
(4)
AB∥CD
随堂练习
那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢?
……
正n边形
(5-2)×180°
5
=108°
(6-2)×180°
6
=120°
(8-2)×180°
8
=135°
(n-2)×180°
n
Now I can ……
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5=吗?你是怎样得到的?
(1)小明每从一条街道转到下一条街道时,身体转过的角是 哪 个 角?
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
D'
A'
C'
E'
B'
O
β
γ
δ
θ
α
A
B
C
D
E
1
2
3
4
5
结论:
?1, ? 2, ? 3, ? 4, ? 5的和等于360?
多边形 内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的外角和等于360?
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
多边形的外角和
A3
A8
An
A1
A2
A7
A5
A6
A4
各抒己见
多边形的外角和等于360?
多边形 外角与内角有何关系?还有其他方法可以推导出多边形外角和?
多边形的任何一个内角加上与它相邻的内角都等于180°(平角),n个外角连同它们的各自相邻的内角,共有n个180°,总和为n× 180° ,再用它减去n个内角的和,剩下的就是多边形的外角和了!
1.正五边形 的每一个外角等于___.每一个内角等于_____,
72°
144°
2.如果一个正多边形的一个内角等于120°,则这个多边 形的边 数是_____
6
3.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____
A.12 B.9 C. 8 D.7
A
3.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____
12
随堂练习
学习了本节课你有哪些 收获?
1. P24-25 2,3,5,6
7,8,9,10
2.阅读P26
作 业
课后思考
1、小明在计算某个多边形的内角和时,由于
粗心他漏掉一个内角,求得的内角和1680° ,你能否求得正确结果呢?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定
