华师版九年级上册数学第24章解直角三角形全章复习课件(共22张PPT)
文档属性
| 名称 | 华师版九年级上册数学第24章解直角三角形全章复习课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 20:15:38 | ||
图片预览




文档简介
(共22张PPT)
解直角三角形
全章复习
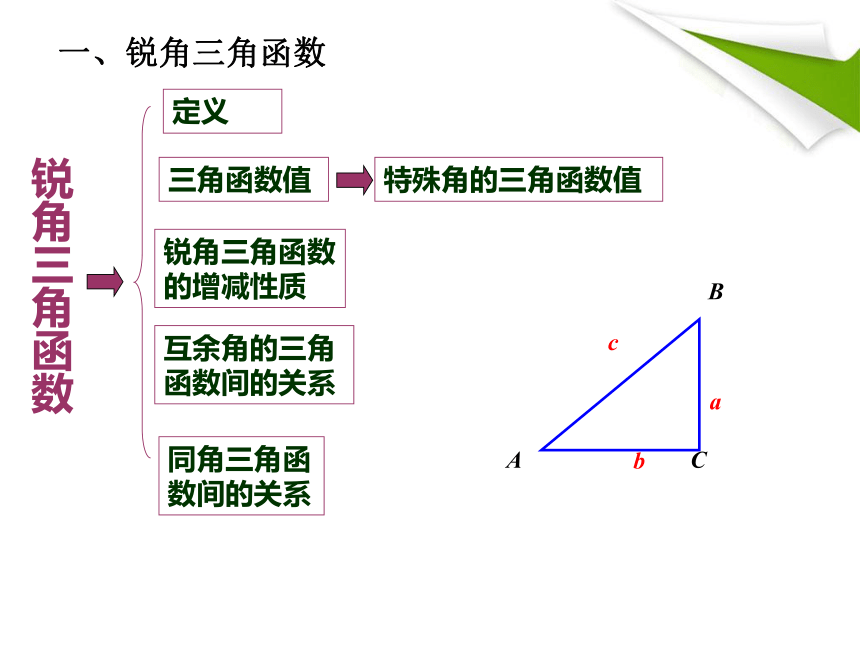
一、锐角三角函数
定义
三角函数值
锐角三角函数的增减性质
锐角三角函数
互余角的三角函数间的关系
同角三角函数间的关系
特殊角的三角函数值
A
B
C
c
a
b
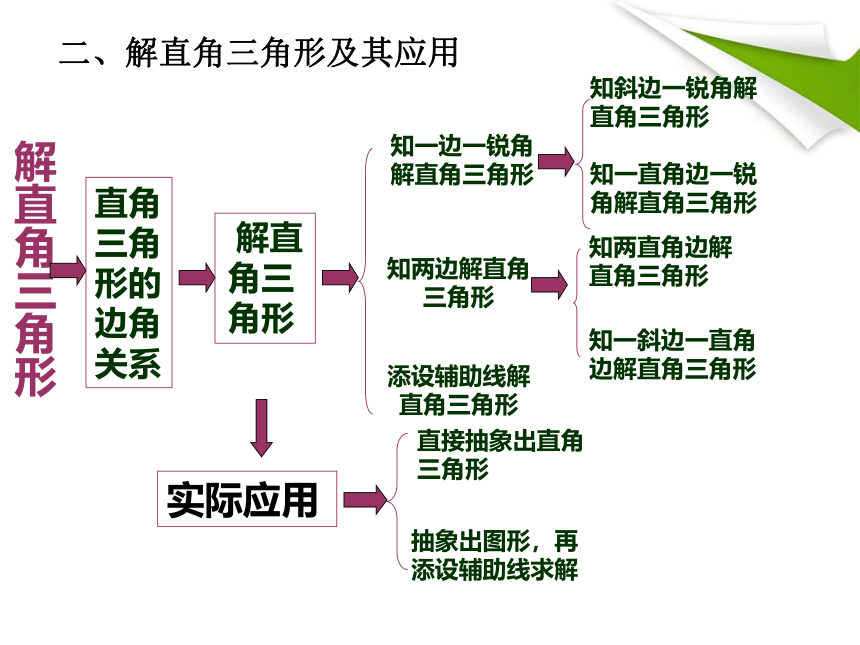
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
解直 角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
直角三角形的边角关系
实际应用
二、解直角三角形及其应用
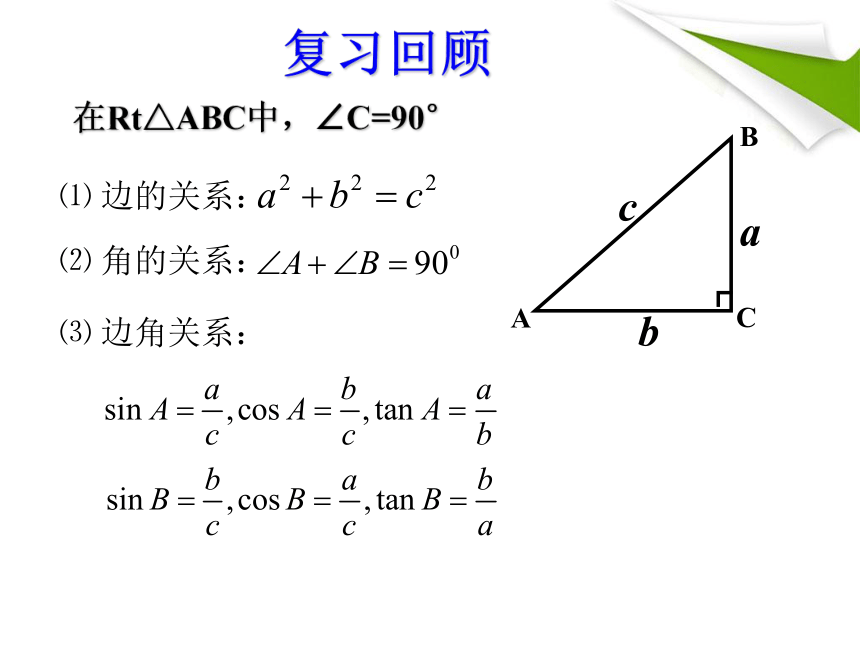
⑴ 边的关系:
⑵ 角的关系:
⑶ 边角关系:
A
B
b
a
c
┏
C
复习回顾
在Rt△ABC中,∠C=90°
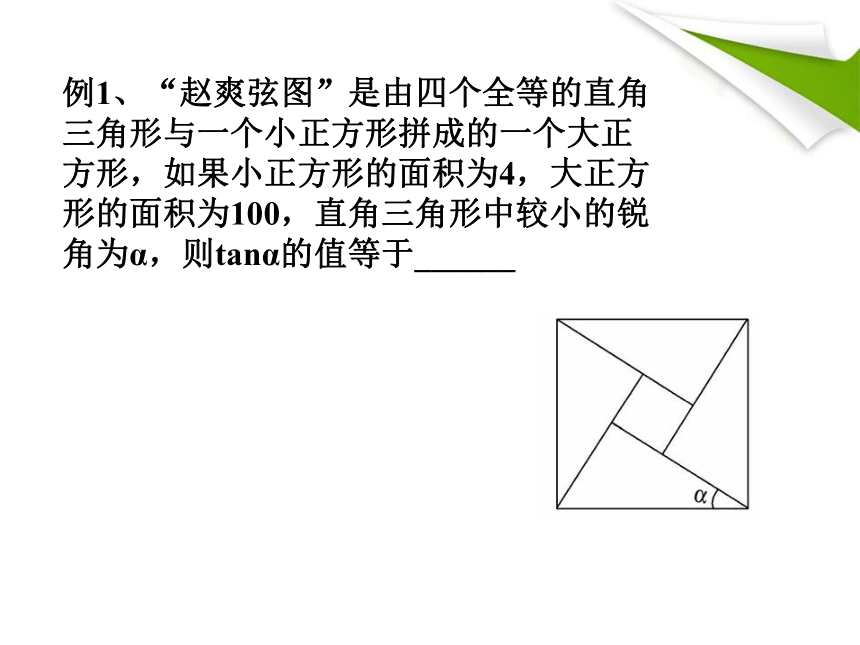
例1、“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于______
例2、
A. 等腰非等边三角形 B. 等边三角形
C. 直角非等腰三角形 D. 等腰直角三角形
例3、 α为锐角,若m>2,下列四个等式中
不可能成立的是( )
例6、在△ABC中,AC=3,AB=2,∠A=60°,
求sin C。
2019/12/31
10
D
解:过B作BD⊥AC于点D
AD=AB·cosA= =1
在Rt△BCD中,∠BDC=90°
BC=
BD=AB·sinA=2× =
CD=AC-AD=3-1=2
在Rt△ABD中,∠ADB=90°
2019/12/31
11
例1、在△ABC中,AC=3,AB=2,锐角A满
足 ,求sinC。
典型例题
解:过B作BD⊥AC于点D
D
变式1
2
典型例题
例1、在△ABC中,AC=3,AB=2,∠A=120°,
求sin C。
2019/12/31
12
解:过B作BD⊥AC,
交CA的延长线于点D
变式2
D
例7、如图,△ABC中,∠B=30°,∠C=45°,AB=6,求AC的长度。
D
30°
45°
例2、如图,△ABC中,∠B=30°,∠C=15°,AB=6,求AC的长度。
典型例题
变 式
D
45°
30°
15°
2019/12/31
15
D
D
基本模型
2019/12/31
16
例8、当 时,下列关系式中
有且仅有一个正确。
(1)正确选项是 ;
A.
B.
C.
C
综合运用
2019/12/31
17
C.
(2)如图,△ABC 中,AC=1,∠B =30°,
,请利用此图证明(1)中的结论;
D
E
1
2019/12/31
18
C.
(3)两块分别含45°和30°的直角三角板如图方式放置在同一平面内,已知 ,根据(1)中结论求 .
E
一般三角形
2019/12/31
19
课堂小结
构造直角
三角形
直角三角形
边:勾股定理
三角函数关系式
角:两锐角互余
边角:三角函数
数量关系
特殊的
拓展练习
练习1、在△ABC中,AB=4,BC= ,
AC=5,求 cosA 。
2019/12/31
20
解:过B作BD⊥AC于点D
D
拓展练习
练习2、在△ABC中,AC=20, , ,
求边AB、BC的值。
2019/12/31
21
解:过B作BD⊥AC于点D
D
巩固练习
练习3、在△ABC中,AC=3,AB=2,∠C=30°,求BC的长。
2019/12/31
22
解:过A作AD⊥BC于点D
C
A
30°
B
3
B’
D
2
2
解直角三角形
全章复习
一、锐角三角函数
定义
三角函数值
锐角三角函数的增减性质
锐角三角函数
互余角的三角函数间的关系
同角三角函数间的关系
特殊角的三角函数值
A
B
C
c
a
b
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
解直 角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
直角三角形的边角关系
实际应用
二、解直角三角形及其应用
⑴ 边的关系:
⑵ 角的关系:
⑶ 边角关系:
A
B
b
a
c
┏
C
复习回顾
在Rt△ABC中,∠C=90°
例1、“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于______
例2、
A. 等腰非等边三角形 B. 等边三角形
C. 直角非等腰三角形 D. 等腰直角三角形
例3、 α为锐角,若m>2,下列四个等式中
不可能成立的是( )
例6、在△ABC中,AC=3,AB=2,∠A=60°,
求sin C。
2019/12/31
10
D
解:过B作BD⊥AC于点D
AD=AB·cosA= =1
在Rt△BCD中,∠BDC=90°
BC=
BD=AB·sinA=2× =
CD=AC-AD=3-1=2
在Rt△ABD中,∠ADB=90°
2019/12/31
11
例1、在△ABC中,AC=3,AB=2,锐角A满
足 ,求sinC。
典型例题
解:过B作BD⊥AC于点D
D
变式1
2
典型例题
例1、在△ABC中,AC=3,AB=2,∠A=120°,
求sin C。
2019/12/31
12
解:过B作BD⊥AC,
交CA的延长线于点D
变式2
D
例7、如图,△ABC中,∠B=30°,∠C=45°,AB=6,求AC的长度。
D
30°
45°
例2、如图,△ABC中,∠B=30°,∠C=15°,AB=6,求AC的长度。
典型例题
变 式
D
45°
30°
15°
2019/12/31
15
D
D
基本模型
2019/12/31
16
例8、当 时,下列关系式中
有且仅有一个正确。
(1)正确选项是 ;
A.
B.
C.
C
综合运用
2019/12/31
17
C.
(2)如图,△ABC 中,AC=1,∠B =30°,
,请利用此图证明(1)中的结论;
D
E
1
2019/12/31
18
C.
(3)两块分别含45°和30°的直角三角板如图方式放置在同一平面内,已知 ,根据(1)中结论求 .
E
一般三角形
2019/12/31
19
课堂小结
构造直角
三角形
直角三角形
边:勾股定理
三角函数关系式
角:两锐角互余
边角:三角函数
数量关系
特殊的
拓展练习
练习1、在△ABC中,AB=4,BC= ,
AC=5,求 cosA 。
2019/12/31
20
解:过B作BD⊥AC于点D
D
拓展练习
练习2、在△ABC中,AC=20, , ,
求边AB、BC的值。
2019/12/31
21
解:过B作BD⊥AC于点D
D
巩固练习
练习3、在△ABC中,AC=3,AB=2,∠C=30°,求BC的长。
2019/12/31
22
解:过A作AD⊥BC于点D
C
A
30°
B
3
B’
D
2
2
