广东省肇庆四会市北大公学人教版必修一 第三章第5节 力的分解(共32张PPT)
文档属性
| 名称 | 广东省肇庆四会市北大公学人教版必修一 第三章第5节 力的分解(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-01 16:11:48 | ||
图片预览




文档简介
(共32张PPT)
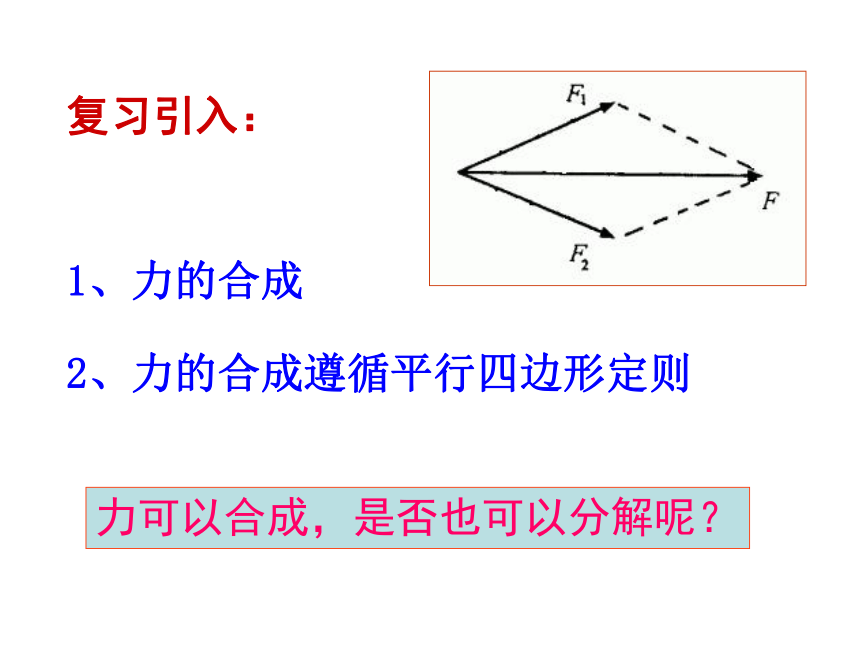
1、请填写以下三角函数关系
及特殊角的值。
边角关系 30° 37° 45° 53° 60°
Sinθ 对边比斜边a/c 0.60 0.80
Cosθ 邻边比斜边b/c 0.80 0.60
tanθ 对边比邻边a/b 1
a
b
c
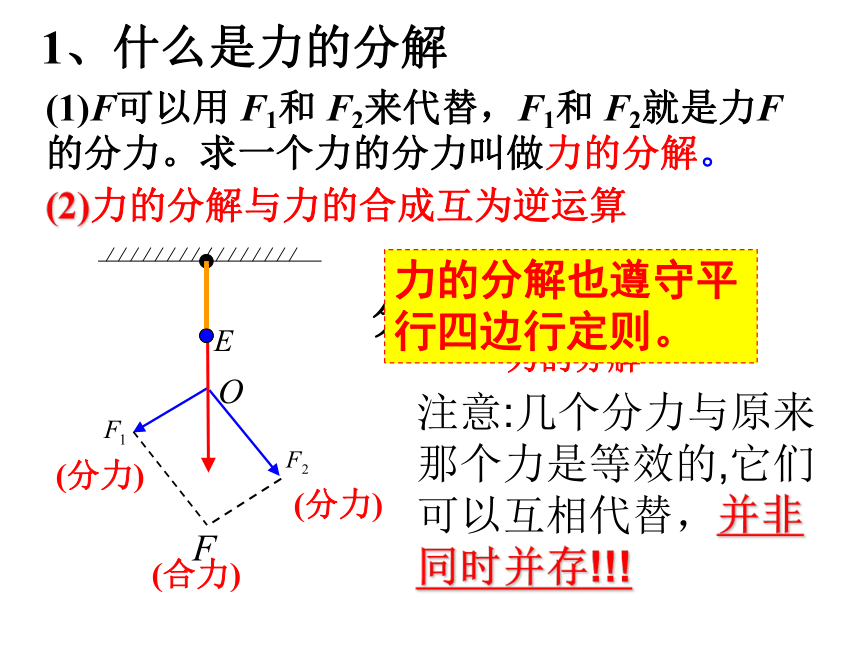
1、力的合成
2、力的合成遵循平行四边形定则
复习引入:
力可以合成,是否也可以分解呢?
五、力的分解
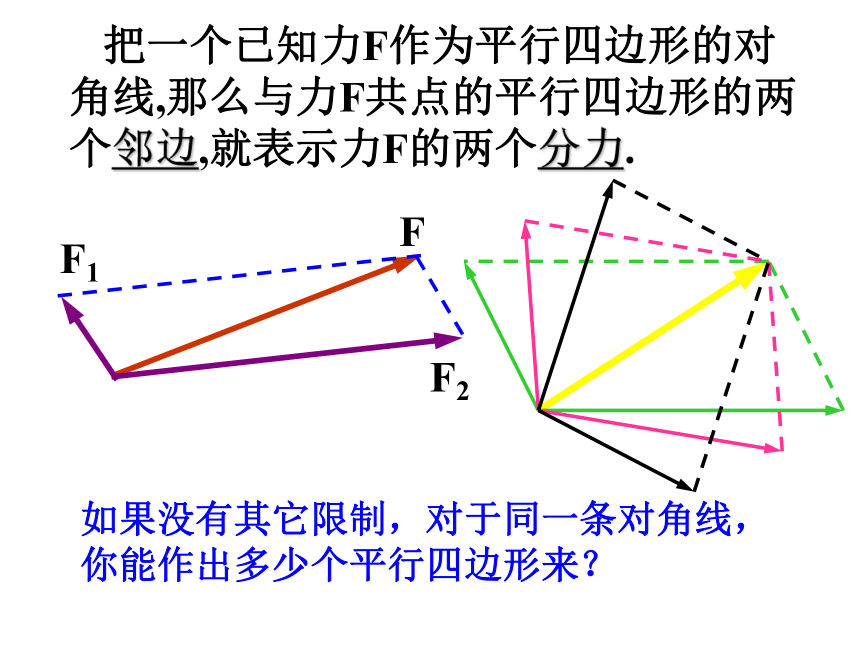
(2)力的分解与力的合成互为逆运算
(1)F可以用 F1和 F2来代替,F1和 F2就是力F的分力。求一个力的分力叫做力的分解。
(合力)
(分力)
(分力)
力的合成
力的分解
分力
合力
1、什么是力的分解
注意:几个分力与原来那个力是等效的,它们可以互相代替,并非同时并存!!!
力的分解也遵守平行四边行定则。
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
F
F1
F2
如果没有其它限制,对于同一条对角线,你能作出多少个平行四边形来?
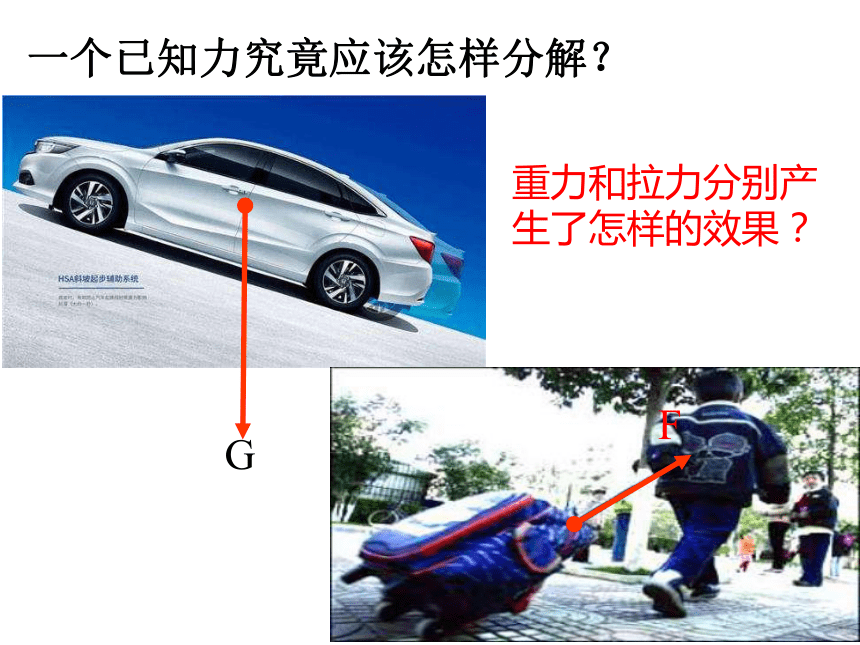
一个已知力究竟应该怎样分解?
G
F
重力和拉力分别产生了怎样的效果?
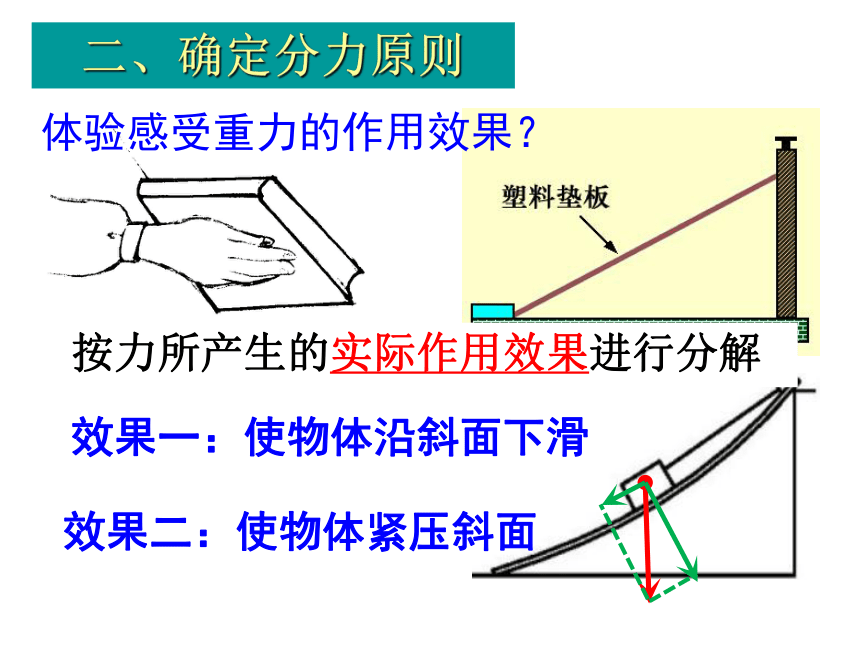
二、确定分力原则
体验感受重力的作用效果?
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
按力所产生的实际作用效果进行分解
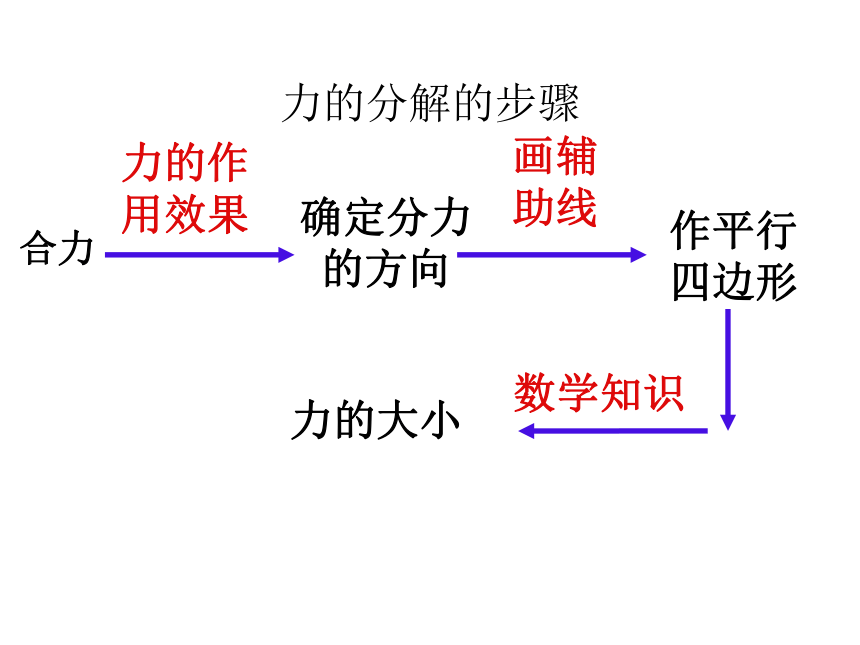
力的分解的步骤
合力
力的作用效果
确定分力的方向
作平行四边形
画辅
助线
力的大小
数学知识
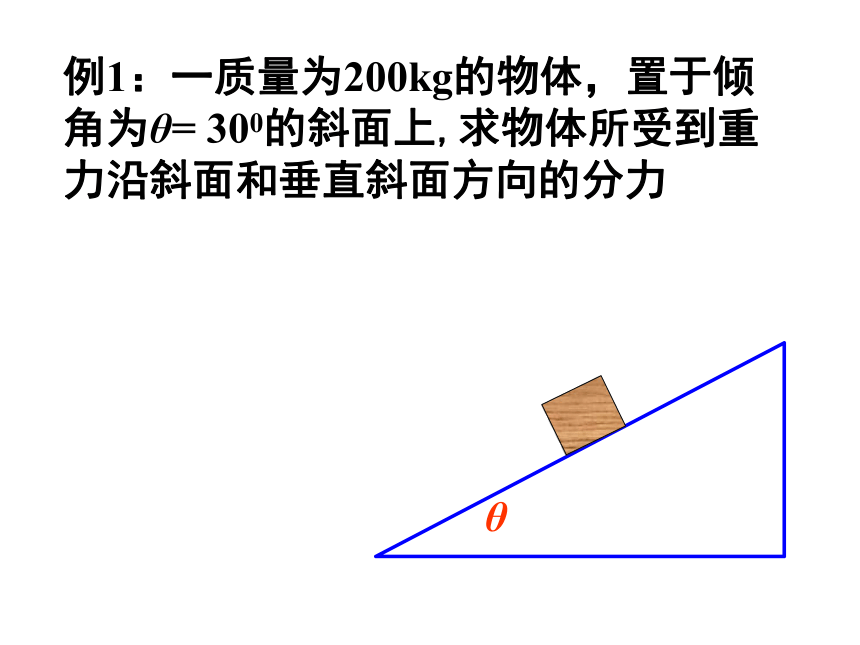
例1:一质量为200kg的物体,置于倾角为θ= 300的斜面上,求物体所受到重力沿斜面和垂直斜面方向的分力
θ
G1
G2
G
θ
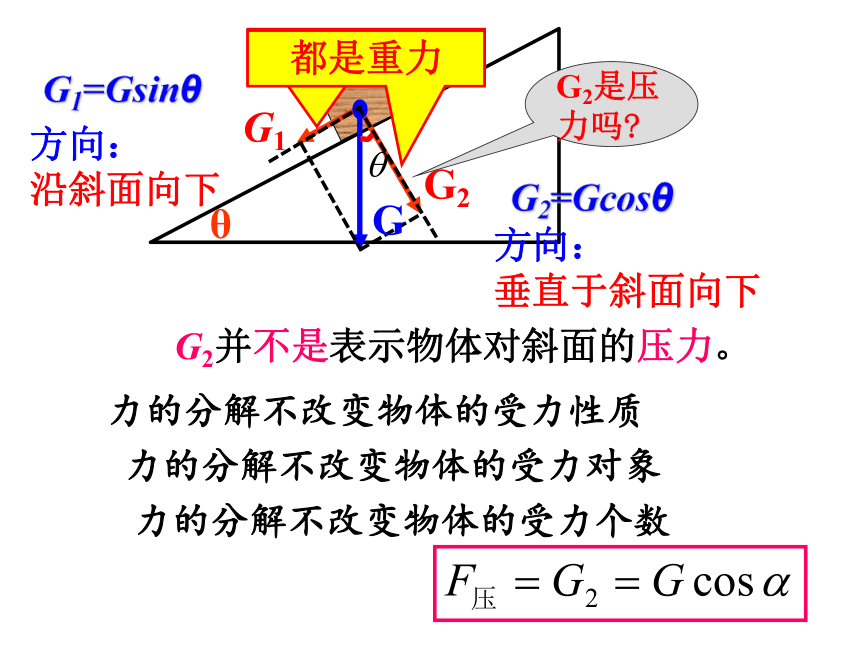
都是重力
G1=Gsinθ
方向:
沿斜面向下
方向:
垂直于斜面向下
G2=Gcosθ
力的分解不改变物体的受力个数
力的分解不改变物体的受力性质
力的分解不改变物体的受力对象
G2并不是表示物体对斜面的压力。
G2是压力吗?
例1:一质量为200kg的物体,置于倾角为θ= 300的斜面上,求物体所受到重力沿斜面和垂直斜面方向的分力
θ
F1=mgsinθ=200×10×0.5N=1000N
F2=mgcosθ=200×10×0.867N=1743N
解:由图示可知:
联系实际:高度一定的桥为什么要造很长的引桥?
当θ角增大时, F1 F2如何变化?
长长的引桥可以减小上坡的倾角,倾角越大,车辆上坡艰难而下坡又不安全。
讨论与交流:用力F 斜向上拉物体,请按力F 产生的效果进行分解。
θ
F
Fx
Fy
F
Fx
Fy
q
例2、三角支架顶端悬一重G的物体, 产生怎样的作用效果?如何分解?求重物的拉力对支架作用大小。
⊙
α
FB
FA
G
动手感受一下
O
B
A
θ
G
G2
G1
轻质支架O点受绳子拉力F作用效果? 如何分解?
我来试试:
F
α
图2
O
F1
F2
三、矢量相加法则:
F合
F1
F2
θ
F1
两个力F1、F2求合力时,首尾依次相连,合力的大小和方向用从第一个力的始端指向第二个力的末端的有向线段表示的方法,叫 力的三角形定则:
既有大小又有方向,相加时遵从平行四边形定则或三角形定则的物理量叫做矢量。
只有大小没有方向,求和时按算术法则相加的物理量叫做标量。
3/11/12
四、三个共点力的合成
①三个力共线且同向时,其合力最大,为F=F1+F2+F3.
②任取两个力F1、F2,求出其合力的范围,
︱F1-F2︱≤ F ≤F1+F2;
如果第三个力F3在这个范围之内,则三个力的合力的最小值为零;
如果第三个力F3不在这个范围内,则合力的最小值为:其中最大的一个力减去另外两个较小的力的代数和.
五、多个力(共点力)的合成方法:
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
F123
F12
F4
F3
F1
F2
F1234
F1
F3
O
F2
x
y
F1y
F1x
F3y
F3x
在很多问题中,常把一个力分解为互相垂直的两个分力,特别是物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力,这样可把复杂问题简化,这种方法叫正交分解法。
F2y
F2x
六、力的正交分解法
(1)原理:把一个已知力沿着两个互相垂直的方向进行分解。
(2)正交分解步骤:
①建立xoy直角坐标系
②沿xoy轴将各力分解
③求x、y轴上的合力Fx,Fy
④最后求Fx和Fy的合力F
大小:
F2y
F1y
F3y
F3x
F1x
F2X
六、力的正交分解法
方向:
(与x轴的夹角)
F
正交分解法的分解原则:
物体受多个力时,应使尽量多的力落在坐标轴上,以减少分解力的运算过程。
练习1、(多选)两个力的大小分别为3N、5N,其合力大小可能是( )
A、1N B、3N C、5N D、9N
练习2、两个共点力,一个是40 N,另一个未知,合力大小是100 N,则另一个力可能是( )
A.20 N B.40 N
C.80 N D.150 N
练习题:共点力的合成
BC
C
练习3.按下列两种情况把一个竖直向下的180 N的力分解为两个分力.
(1)一个分力在水平方向上,并等于240 N,求另一个分力的大小和方向;
(2)一个分力在水平方向上,另一个分力与竖直方向的夹角为30°斜向下,求两个分力的大小.
(1) (2)
12
练习4
三个力的合力范围怎么求?
①3N、4N、5N;
②2N、5N、6N;
③8N、4N、3N;
④1N、5N、9N;
①0N≤F≤12N;
②0N≤F≤13N;
③1N≤F≤15N;
④3N≤F≤15N;
例5、斜面倾角 ,物体沿斜面匀速下滑,证明物体与斜面间动摩擦因素,
α
(1)对物体进行受力分析
(2)求物体受到的支持力FN
(3)求物体受到的摩擦力f
(4)物体的合力
.
3\10\11//22
作业:课本P66 T1 T2
练习:
创新设计和分层训练上相关练习题
【例题 】木箱重600 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。
30°
F
F
G
F
f
F
N
F
1
F
2
解:画出物体受力图,如图所示。
把力F 分解为沿水平方向的分力F 和沿竖直方向的分力F 。
2
1
学以致用
由于物体在水平方向和竖直方向都处于平衡状态,所以
F
G
F
f
F
N
F
1
F
2
拓展练习:
1.两个力夹角θ一定,F1不变,仅增大F2,其合力F怎么变化?
②当θ>90°时,可能F合 先变小后变大;
可能 增大 。
F合
F2
F1
F2
θ
F1
F2
F2
θ
F合
①当θ≤90°时,F合变大。
F合
2、F1大小、方向一定,F合方向一定,问力F2怎样施加才最小?
F2
F1
1、请填写以下三角函数关系
及特殊角的值。
边角关系 30° 37° 45° 53° 60°
Sinθ 对边比斜边a/c 0.60 0.80
Cosθ 邻边比斜边b/c 0.80 0.60
tanθ 对边比邻边a/b 1
a
b
c
1、力的合成
2、力的合成遵循平行四边形定则
复习引入:
力可以合成,是否也可以分解呢?
五、力的分解
(2)力的分解与力的合成互为逆运算
(1)F可以用 F1和 F2来代替,F1和 F2就是力F的分力。求一个力的分力叫做力的分解。
(合力)
(分力)
(分力)
力的合成
力的分解
分力
合力
1、什么是力的分解
注意:几个分力与原来那个力是等效的,它们可以互相代替,并非同时并存!!!
力的分解也遵守平行四边行定则。
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
F
F1
F2
如果没有其它限制,对于同一条对角线,你能作出多少个平行四边形来?
一个已知力究竟应该怎样分解?
G
F
重力和拉力分别产生了怎样的效果?
二、确定分力原则
体验感受重力的作用效果?
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
按力所产生的实际作用效果进行分解
力的分解的步骤
合力
力的作用效果
确定分力的方向
作平行四边形
画辅
助线
力的大小
数学知识
例1:一质量为200kg的物体,置于倾角为θ= 300的斜面上,求物体所受到重力沿斜面和垂直斜面方向的分力
θ
G1
G2
G
θ
都是重力
G1=Gsinθ
方向:
沿斜面向下
方向:
垂直于斜面向下
G2=Gcosθ
力的分解不改变物体的受力个数
力的分解不改变物体的受力性质
力的分解不改变物体的受力对象
G2并不是表示物体对斜面的压力。
G2是压力吗?
例1:一质量为200kg的物体,置于倾角为θ= 300的斜面上,求物体所受到重力沿斜面和垂直斜面方向的分力
θ
F1=mgsinθ=200×10×0.5N=1000N
F2=mgcosθ=200×10×0.867N=1743N
解:由图示可知:
联系实际:高度一定的桥为什么要造很长的引桥?
当θ角增大时, F1 F2如何变化?
长长的引桥可以减小上坡的倾角,倾角越大,车辆上坡艰难而下坡又不安全。
讨论与交流:用力F 斜向上拉物体,请按力F 产生的效果进行分解。
θ
F
Fx
Fy
F
Fx
Fy
q
例2、三角支架顶端悬一重G的物体, 产生怎样的作用效果?如何分解?求重物的拉力对支架作用大小。
⊙
α
FB
FA
G
动手感受一下
O
B
A
θ
G
G2
G1
轻质支架O点受绳子拉力F作用效果? 如何分解?
我来试试:
F
α
图2
O
F1
F2
三、矢量相加法则:
F合
F1
F2
θ
F1
两个力F1、F2求合力时,首尾依次相连,合力的大小和方向用从第一个力的始端指向第二个力的末端的有向线段表示的方法,叫 力的三角形定则:
既有大小又有方向,相加时遵从平行四边形定则或三角形定则的物理量叫做矢量。
只有大小没有方向,求和时按算术法则相加的物理量叫做标量。
3/11/12
四、三个共点力的合成
①三个力共线且同向时,其合力最大,为F=F1+F2+F3.
②任取两个力F1、F2,求出其合力的范围,
︱F1-F2︱≤ F ≤F1+F2;
如果第三个力F3在这个范围之内,则三个力的合力的最小值为零;
如果第三个力F3不在这个范围内,则合力的最小值为:其中最大的一个力减去另外两个较小的力的代数和.
五、多个力(共点力)的合成方法:
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
F123
F12
F4
F3
F1
F2
F1234
F1
F3
O
F2
x
y
F1y
F1x
F3y
F3x
在很多问题中,常把一个力分解为互相垂直的两个分力,特别是物体受多个力作用时,把物体受到的各个力都分解到互相垂直的两个方向上去,然后求两个方向上的力的合力,这样可把复杂问题简化,这种方法叫正交分解法。
F2y
F2x
六、力的正交分解法
(1)原理:把一个已知力沿着两个互相垂直的方向进行分解。
(2)正交分解步骤:
①建立xoy直角坐标系
②沿xoy轴将各力分解
③求x、y轴上的合力Fx,Fy
④最后求Fx和Fy的合力F
大小:
F2y
F1y
F3y
F3x
F1x
F2X
六、力的正交分解法
方向:
(与x轴的夹角)
F
正交分解法的分解原则:
物体受多个力时,应使尽量多的力落在坐标轴上,以减少分解力的运算过程。
练习1、(多选)两个力的大小分别为3N、5N,其合力大小可能是( )
A、1N B、3N C、5N D、9N
练习2、两个共点力,一个是40 N,另一个未知,合力大小是100 N,则另一个力可能是( )
A.20 N B.40 N
C.80 N D.150 N
练习题:共点力的合成
BC
C
练习3.按下列两种情况把一个竖直向下的180 N的力分解为两个分力.
(1)一个分力在水平方向上,并等于240 N,求另一个分力的大小和方向;
(2)一个分力在水平方向上,另一个分力与竖直方向的夹角为30°斜向下,求两个分力的大小.
(1) (2)
12
练习4
三个力的合力范围怎么求?
①3N、4N、5N;
②2N、5N、6N;
③8N、4N、3N;
④1N、5N、9N;
①0N≤F≤12N;
②0N≤F≤13N;
③1N≤F≤15N;
④3N≤F≤15N;
例5、斜面倾角 ,物体沿斜面匀速下滑,证明物体与斜面间动摩擦因素,
α
(1)对物体进行受力分析
(2)求物体受到的支持力FN
(3)求物体受到的摩擦力f
(4)物体的合力
.
3\10\11//22
作业:课本P66 T1 T2
练习:
创新设计和分层训练上相关练习题
【例题 】木箱重600 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。
30°
F
F
G
F
f
F
N
F
1
F
2
解:画出物体受力图,如图所示。
把力F 分解为沿水平方向的分力F 和沿竖直方向的分力F 。
2
1
学以致用
由于物体在水平方向和竖直方向都处于平衡状态,所以
F
G
F
f
F
N
F
1
F
2
拓展练习:
1.两个力夹角θ一定,F1不变,仅增大F2,其合力F怎么变化?
②当θ>90°时,可能F合 先变小后变大;
可能 增大 。
F合
F2
F1
F2
θ
F1
F2
F2
θ
F合
①当θ≤90°时,F合变大。
F合
2、F1大小、方向一定,F合方向一定,问力F2怎样施加才最小?
F2
F1
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
