高中数学人教版必修1课件:2.1.1指对运算及性质(共24张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:2.1.1指对运算及性质(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
情境再现:
在我们的数学学习过程中,我们可以清晰的发现数字如何一步一步的由自然数扩充为整数、有理数、实数.
在数系的扩充过程中,伴随的是各种运算的出现----加、减、乘、除、幂运算.
情境再现:
有三个数3(底),2(指数)和9(幂)
(1)由底数,指数得到幂的运算是
(2)由幂和指数得到底数的运算是
乘方 运算。
开方运算。
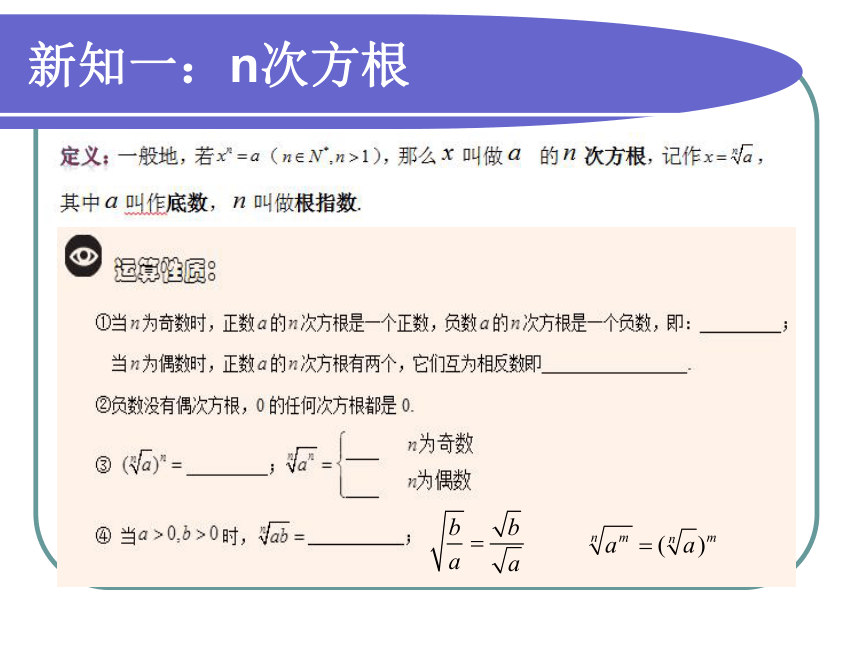
新知一:n次方根
新知二:分数指数幂
我们发现:当a>0时,
分指开方,负指取倒!
无法开方的根式全部分指化!
新知二:分数指数幂
类似的当指数为无理数时,
也是一个确实的实数且符合运算性质:
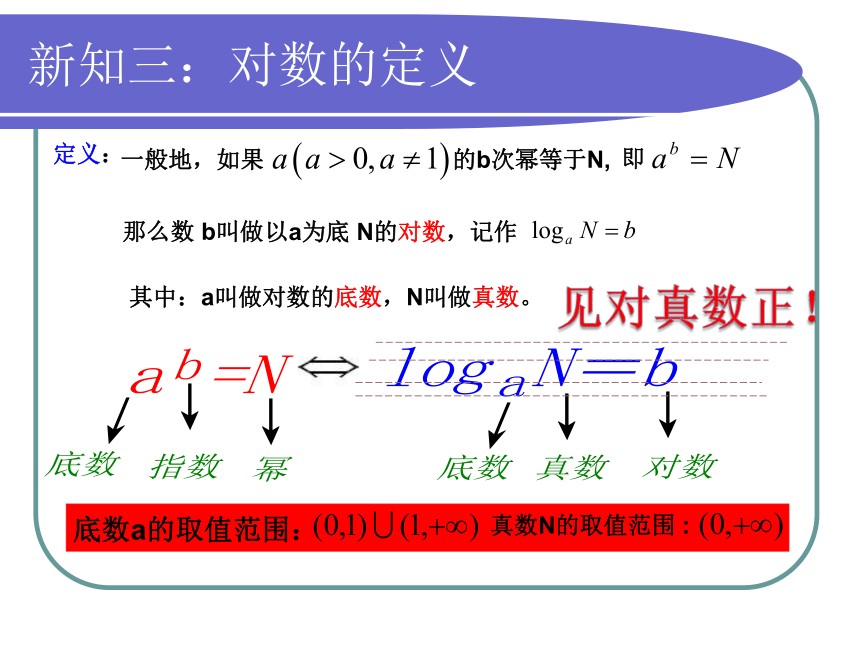
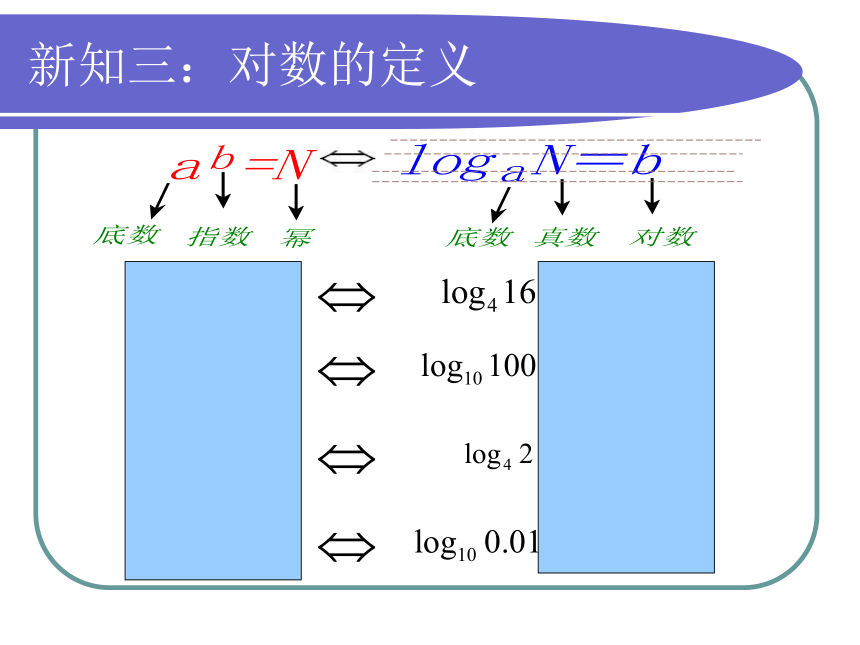
新知三:对数的定义
有三个数3(底),2(指数)和9(幂)
(1)由底数,指数得到幂的运算是
(2)由幂和指数得到底数的运算是
乘方 运算。
开方运算。
(2)由幂和底数得到指数的运算是
什么运算?
一般地,如果
的b次幂等于N,
那么数 b叫做
以a为底 N的对数,记作
其中:a叫做对数的底数,N叫做真数。
定义:
即
底数a的取值范围:
真数N的取值范围 :
新知三:对数的定义
见对真数正!
新知三:对数的定义
新知四:常见对数(对数恒等式)
⑴负数与零没有对数(∵在指数式中 N > 0 )
⑵
对任意
且
都有
⑶两个对数恒等式
如果把
中的 b写成
则有:
如果把
中的 N写成
则有:
新知四:常见对数(对数恒等式)
⑷常用对数:
我们通常将以10为底的对数叫做常用对数。
为了简便,N的常用对数
简记作lgN。
例如:
简记作lg5;
简记作lg3.5.
⑸自然对数:
在科学技术中常常使用以无理数e=2.71828……
为底的对数,以e为底的对数叫自然对数。
为了简便,N的自然对数
简记作lnN。
例如:
简记作ln3 ;
简记作ln10
⑴给出四个等式:
其中正确的是________
⑵
⑶
⑷
1) ,2)
4
3
?
新知五:对数运算公式
同底对数相加减等于底数不变,真数相乘除
同底数幂相乘除等于底数不变,指数相加减
新知五:对数运算公式
次数前移做倍数,倍数后移做次幂
取幂再幂等于指数相乘
新知五:对数运算公式
特殊地:
换底公式
真底互换变倒数
新知五:对数运算公式
指数运算公式a>0 对数运算 公式
新知五:对数运算公式
P65 例3.例4
P68 练习1-4
分指开方
负指取倒
指对运算小结
分指的定义
两个特殊的式子
三个指数运算公式
对数的定义
四个对数恒等式
三个对数运算公式
新知四:常见对数(对数恒等式)
求对数值
解指对数方程
P64 练习3.4
P68 练习1.2.3.4
情境再现:
在我们的数学学习过程中,我们可以清晰的发现数字如何一步一步的由自然数扩充为整数、有理数、实数.
在数系的扩充过程中,伴随的是各种运算的出现----加、减、乘、除、幂运算.
情境再现:
有三个数3(底),2(指数)和9(幂)
(1)由底数,指数得到幂的运算是
(2)由幂和指数得到底数的运算是
乘方 运算。
开方运算。
新知一:n次方根
新知二:分数指数幂
我们发现:当a>0时,
分指开方,负指取倒!
无法开方的根式全部分指化!
新知二:分数指数幂
类似的当指数为无理数时,
也是一个确实的实数且符合运算性质:
新知三:对数的定义
有三个数3(底),2(指数)和9(幂)
(1)由底数,指数得到幂的运算是
(2)由幂和指数得到底数的运算是
乘方 运算。
开方运算。
(2)由幂和底数得到指数的运算是
什么运算?
一般地,如果
的b次幂等于N,
那么数 b叫做
以a为底 N的对数,记作
其中:a叫做对数的底数,N叫做真数。
定义:
即
底数a的取值范围:
真数N的取值范围 :
新知三:对数的定义
见对真数正!
新知三:对数的定义
新知四:常见对数(对数恒等式)
⑴负数与零没有对数(∵在指数式中 N > 0 )
⑵
对任意
且
都有
⑶两个对数恒等式
如果把
中的 b写成
则有:
如果把
中的 N写成
则有:
新知四:常见对数(对数恒等式)
⑷常用对数:
我们通常将以10为底的对数叫做常用对数。
为了简便,N的常用对数
简记作lgN。
例如:
简记作lg5;
简记作lg3.5.
⑸自然对数:
在科学技术中常常使用以无理数e=2.71828……
为底的对数,以e为底的对数叫自然对数。
为了简便,N的自然对数
简记作lnN。
例如:
简记作ln3 ;
简记作ln10
⑴给出四个等式:
其中正确的是________
⑵
⑶
⑷
1) ,2)
4
3
?
新知五:对数运算公式
同底对数相加减等于底数不变,真数相乘除
同底数幂相乘除等于底数不变,指数相加减
新知五:对数运算公式
次数前移做倍数,倍数后移做次幂
取幂再幂等于指数相乘
新知五:对数运算公式
特殊地:
换底公式
真底互换变倒数
新知五:对数运算公式
指数运算公式a>0 对数运算 公式
新知五:对数运算公式
P65 例3.例4
P68 练习1-4
分指开方
负指取倒
指对运算小结
分指的定义
两个特殊的式子
三个指数运算公式
对数的定义
四个对数恒等式
三个对数运算公式
新知四:常见对数(对数恒等式)
求对数值
解指对数方程
P64 练习3.4
P68 练习1.2.3.4
