高中数学人教版必修1课件:1.3.1单调性(共27张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:1.3.1单调性(共27张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 431.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 11:39:22 | ||
图片预览






文档简介
(共27张PPT)
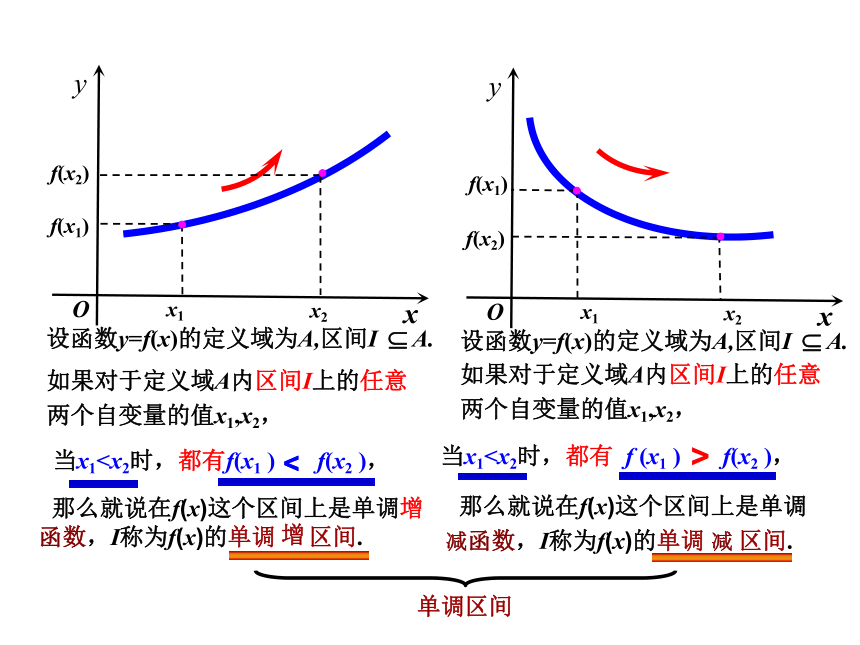
考试次数 1 2 3 4 5
速写成绩 1 2 3 4 5
考试次数 1 2 3 4 5
素描成绩 5 4 3 2 1
函数的单调性
O
x
y
y
O
x
O
x
y
-1
y
O
x
局部上升或下降
图象上扬
图象下降
根据下列函数图象,指出其变化趋势.
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?
图象在该区间呈上升趋势
当x的值增大时,函数值y也增大
图象在该区间呈下降趋势
当x的值增大时,函数值y反而减小
图形
定性
在某一区间D内(D 定义域),
怎样定量表述函数y= f(x) 在区间 D上,
函数值 y 随 自变量x的增大而增大呢?
x1,x2
当x1
图象在区间D逐渐上升
?
O
x
D
y
区间D内随着x的增大,y也增大
x1
x2
f(x1)
f(x2)
M
N
都
任意
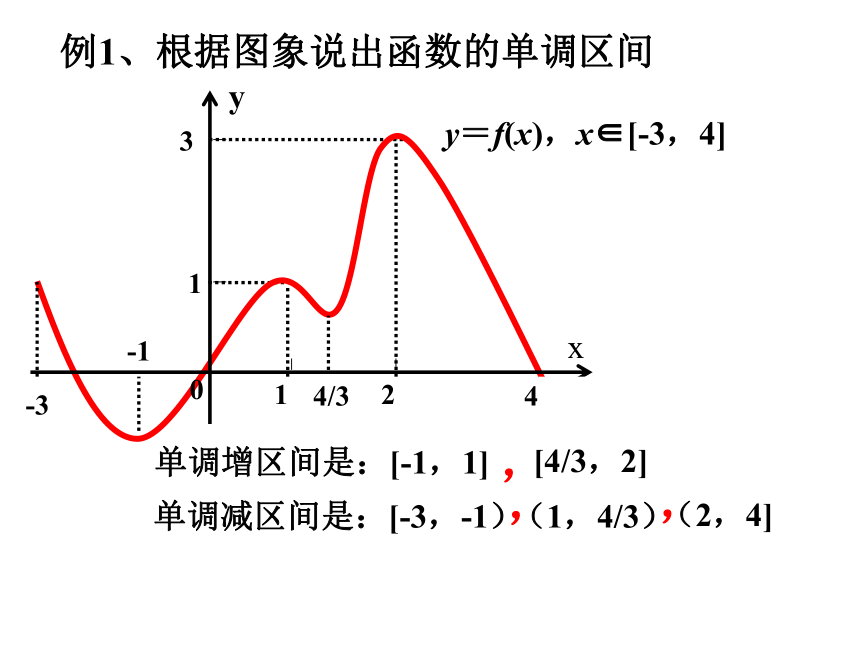
那么就说在f(x)这个区间上是单调
减函数,I称为f(x)的单调 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为A,区间I A.
如果对于定义域A内区间I上的任意
两个自变量的值x1,x2,
设函数y=f(x)的定义域为A,区间I A.
如果对于定义域A内区间I上的任意
两个自变量的值x1,x2,
那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.
增
当x1<
当x1<
>
单调区间
(1)函数单调性是针对某个区间而言的,是一个局
部性质;
(5)如果一个函数在整个定义域上具有单调性,则称这个函数为单调函数。
注意:
(3)答案格式:增(减)区间是:[a,b]。
多个单调区间之间只能用逗号隔开,不能用“U”
(2)单调区间是定义域的子集,所以单调区间一定
是某段x的取值范围!
(4)区间端点只要函数有意义,都可以带上,但一般
不重复出现。
x
y
2
1
0
1
3
-3
-1
4
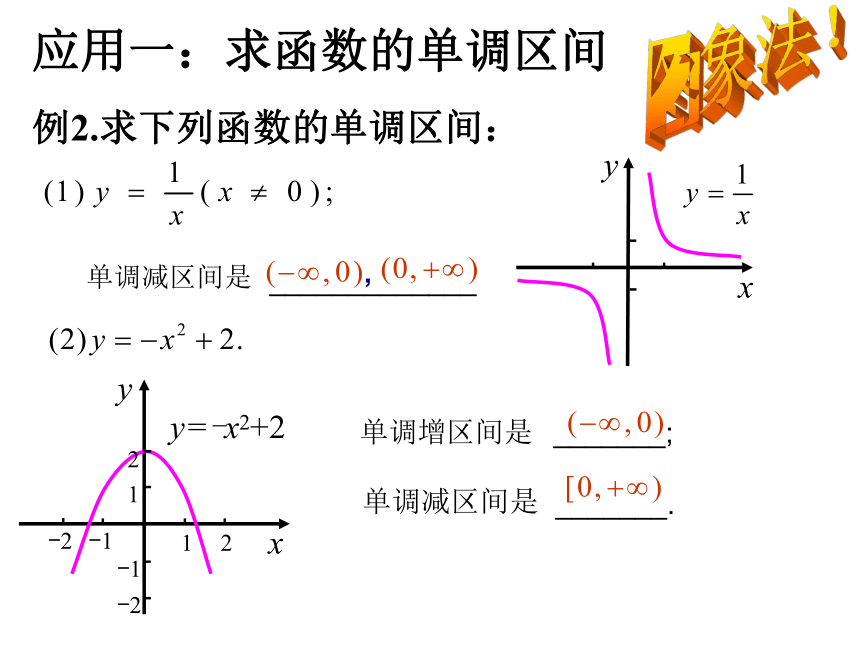
例1、根据图象说出函数的单调区间
y=f(x),x∈[-3,4]
单调增区间是:[-1,1]
(1,4/3)
(2,4]
,
[4/3,2]
4/3
单调减区间是:[-3,-1)
,
,
图象法!
例2.求下列函数的单调区间:
x
y
_____________
,
应用一:求函数的单调区间
x
y
y=-x2+2
1
-1
1
2
2
-1
-2
-2
_______;
_______.
函数 单调区间 是否单调函数
k >0时:
k <0时:
k >0时:
k <0时:
是
不是
不是
1. 求函数y=-x2+2|x|+3的单调区间.
y
0
x
-1
1
解:
增区间是:(-∞,-1]和[0,1]
减区间是:[-1,0]和[1,+∞)
练一练
2. 求函数 的单调区间
应用一:求函数的单调区间
单调性性质规律总结:
若函数f(x),g(x)在给定的区间上具有单调性,利用增(减)函数的定义容易证得,在这个区间上:
(1)函数f(x)与f(x)+C(C为常数)具有相同的单调性.
(2)C>0时,函数f(x)与C·f(x)具有相同的单调性;
C<0时,函数 f(x)与C·f(x)具有相反的单调性.
(3)若函数f(x),g(x)都是增(减)函数,则f(x)+g(x)仍是增(减)函数.
性质法!
因为增加增=增
所以:
目前无法判断增减
复合函数的单调性:对于复合函数f[g(x)],
t=g(x) 增↑ 增 ↑ 减↓ 减 ↓
y=f(t) 增↑ 减↓ 增↑ 减↓
y=f[g(x)] 增↑ 减 ↓ 减 ↓ 增 ↑
同增异减
因为外围函数纯增,
所以t的范围可省略
复合函数的单调性:对于复合函数f[g(x)],
t=g(x) 增↑ 增 ↑ 减↓ 减 ↓
y=f(t) 增↑ 减↓ 增↑ 减↓
y=f[g(x)] 增↑ 减 ↓ 减 ↓ 增 ↑
书写:
因为t=g(x)在 上增,
y=f(t) 在 上增,
所以y=f[g(x)]在 上增
同增异减
例5:
求函数y=f(x)在R上是减函数,求y=f(1-x)的单调递增区间。
例4:
求函数y= 的单调区间
求函数y=x4+2x2 +18的单调区间
例6:
复合求单调先求定义域!
解:因为 ,所以函数定义域为:
设 则
因为:内围函数在 上减,在 上增,
外围函数纯增,(因为外围纯增所以省略了t的相应范围)
所以:复合函数在 上减,在 上增,
应用一:求函数的单调区间
定义法!
证明:在区间 上任取两个值 且
则
,且
所以函数 在区间上 是增函数.
区间设值
作差变形
定号
结论
例3:判断函数 在定义域 上的单调性.
证明函数单调性的四步骤:
(1)设值:
设 (大小和区间)
(2)比较:
作差 ,通分或因式分解
(3)定号:
(判断的 符号)
(4)结论:
(作出单调性的结论)
作业
P39 习题1.3 A组2.3题,B组1题
1、
2、
若二次函数 的单调增区间是 , 则a的取值情况是( )
应用二:单调性求参
若二次函数 在区间 上单调递增,求a的取值范围。
o
x
y
1
x
y
1
o
1、
2、
3、
4、
若二次函数 的单调增区间是 , 则a的取值情况是 ( )
应用二:单调性求参
若二次函数 在区间 上单调递增,求a的取值范围。
应用三:通过单调性比较大小
和解不等式
1、函数f(x)在 上是减函数,求f(a2-a+1)与 f(3/4)的大小关系
2、
是在R上的单调函数,图象过点A(0,2)和B(3,0)
(1)解方程
(2)解不等式
(3)求适合 的 的取值范围
x、y大小互推
3、f(x)是定义域为[-1,1]上的增函数,解不等式f(x-1)函数必有值域,但不一定有最值:
最值与值域方法相同,结果书写不同。
考试次数 1 2 3 4 5
速写成绩 1 2 3 4 5
考试次数 1 2 3 4 5
素描成绩 5 4 3 2 1
函数的单调性
O
x
y
y
O
x
O
x
y
-1
y
O
x
局部上升或下降
图象上扬
图象下降
根据下列函数图象,指出其变化趋势.
能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?
图象在该区间呈上升趋势
当x的值增大时,函数值y也增大
图象在该区间呈下降趋势
当x的值增大时,函数值y反而减小
图形
定性
在某一区间D内(D 定义域),
怎样定量表述函数y= f(x) 在区间 D上,
函数值 y 随 自变量x的增大而增大呢?
x1,x2
当x1
图象在区间D逐渐上升
?
O
x
D
y
区间D内随着x的增大,y也增大
x1
x2
f(x1)
f(x2)
M
N
都
任意
那么就说在f(x)这个区间上是单调
减函数,I称为f(x)的单调 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为A,区间I A.
如果对于定义域A内区间I上的任意
两个自变量的值x1,x2,
设函数y=f(x)的定义域为A,区间I A.
如果对于定义域A内区间I上的任意
两个自变量的值x1,x2,
那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.
增
当x1
当x1
>
单调区间
(1)函数单调性是针对某个区间而言的,是一个局
部性质;
(5)如果一个函数在整个定义域上具有单调性,则称这个函数为单调函数。
注意:
(3)答案格式:增(减)区间是:[a,b]。
多个单调区间之间只能用逗号隔开,不能用“U”
(2)单调区间是定义域的子集,所以单调区间一定
是某段x的取值范围!
(4)区间端点只要函数有意义,都可以带上,但一般
不重复出现。
x
y
2
1
0
1
3
-3
-1
4
例1、根据图象说出函数的单调区间
y=f(x),x∈[-3,4]
单调增区间是:[-1,1]
(1,4/3)
(2,4]
,
[4/3,2]
4/3
单调减区间是:[-3,-1)
,
,
图象法!
例2.求下列函数的单调区间:
x
y
_____________
,
应用一:求函数的单调区间
x
y
y=-x2+2
1
-1
1
2
2
-1
-2
-2
_______;
_______.
函数 单调区间 是否单调函数
k >0时:
k <0时:
k >0时:
k <0时:
是
不是
不是
1. 求函数y=-x2+2|x|+3的单调区间.
y
0
x
-1
1
解:
增区间是:(-∞,-1]和[0,1]
减区间是:[-1,0]和[1,+∞)
练一练
2. 求函数 的单调区间
应用一:求函数的单调区间
单调性性质规律总结:
若函数f(x),g(x)在给定的区间上具有单调性,利用增(减)函数的定义容易证得,在这个区间上:
(1)函数f(x)与f(x)+C(C为常数)具有相同的单调性.
(2)C>0时,函数f(x)与C·f(x)具有相同的单调性;
C<0时,函数 f(x)与C·f(x)具有相反的单调性.
(3)若函数f(x),g(x)都是增(减)函数,则f(x)+g(x)仍是增(减)函数.
性质法!
因为增加增=增
所以:
目前无法判断增减
复合函数的单调性:对于复合函数f[g(x)],
t=g(x) 增↑ 增 ↑ 减↓ 减 ↓
y=f(t) 增↑ 减↓ 增↑ 减↓
y=f[g(x)] 增↑ 减 ↓ 减 ↓ 增 ↑
同增异减
因为外围函数纯增,
所以t的范围可省略
复合函数的单调性:对于复合函数f[g(x)],
t=g(x) 增↑ 增 ↑ 减↓ 减 ↓
y=f(t) 增↑ 减↓ 增↑ 减↓
y=f[g(x)] 增↑ 减 ↓ 减 ↓ 增 ↑
书写:
因为t=g(x)在 上增,
y=f(t) 在 上增,
所以y=f[g(x)]在 上增
同增异减
例5:
求函数y=f(x)在R上是减函数,求y=f(1-x)的单调递增区间。
例4:
求函数y= 的单调区间
求函数y=x4+2x2 +18的单调区间
例6:
复合求单调先求定义域!
解:因为 ,所以函数定义域为:
设 则
因为:内围函数在 上减,在 上增,
外围函数纯增,(因为外围纯增所以省略了t的相应范围)
所以:复合函数在 上减,在 上增,
应用一:求函数的单调区间
定义法!
证明:在区间 上任取两个值 且
则
,且
所以函数 在区间上 是增函数.
区间设值
作差变形
定号
结论
例3:判断函数 在定义域 上的单调性.
证明函数单调性的四步骤:
(1)设值:
设 (大小和区间)
(2)比较:
作差 ,通分或因式分解
(3)定号:
(判断的 符号)
(4)结论:
(作出单调性的结论)
作业
P39 习题1.3 A组2.3题,B组1题
1、
2、
若二次函数 的单调增区间是 , 则a的取值情况是( )
应用二:单调性求参
若二次函数 在区间 上单调递增,求a的取值范围。
o
x
y
1
x
y
1
o
1、
2、
3、
4、
若二次函数 的单调增区间是 , 则a的取值情况是 ( )
应用二:单调性求参
若二次函数 在区间 上单调递增,求a的取值范围。
应用三:通过单调性比较大小
和解不等式
1、函数f(x)在 上是减函数,求f(a2-a+1)与 f(3/4)的大小关系
2、
是在R上的单调函数,图象过点A(0,2)和B(3,0)
(1)解方程
(2)解不等式
(3)求适合 的 的取值范围
x、y大小互推
3、f(x)是定义域为[-1,1]上的增函数,解不等式f(x-1)
最值与值域方法相同,结果书写不同。
