高中数学人教版必修1课件:1.1.2集合间的关系(共17张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:1.1.2集合间的关系(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
复习回顾
知识回顾
集合与元素的定义
元素的性质
集合的表示
实数有相等关系、大小关系,
如5=5,5<7,5>3,等等,类比实数之间的关系,你会想到集合之间的什么关系?
思考
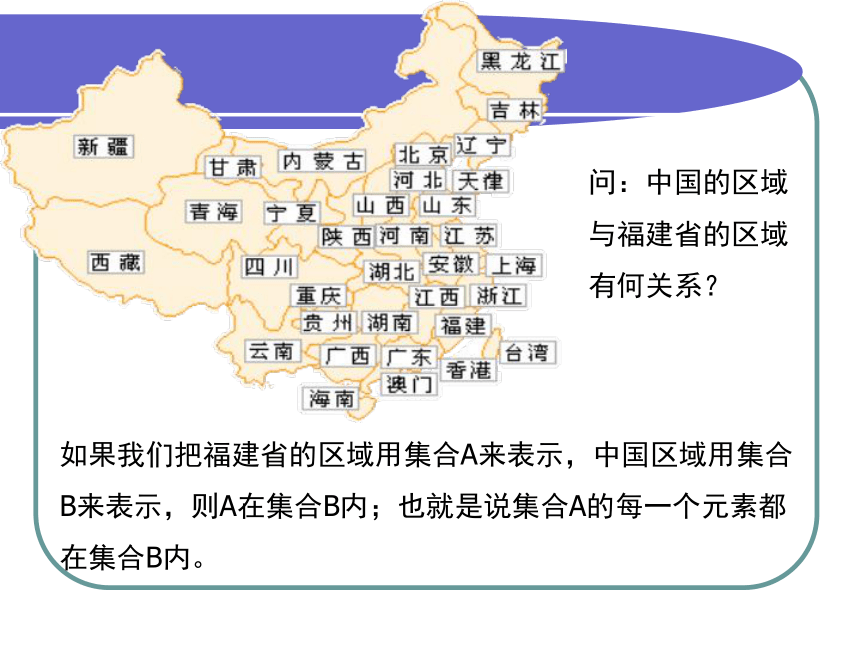
问:中国的区域与福建省的区域有何关系?
如果我们把福建省的区域用集合A来表示,中国区域用集合B来表示,则A在集合B内;也就是说集合A的每一个元素都在集合B内。
中央美术学院附属中学 赵巧
1.1 集 合
1.1.2 集合的关系
一、子集
对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A是集合B的子集,
读作包含于集合B,或者集合B包含集合A
当集合A不是集合B的子集,
记作A B(或B A)
记作A B(或B A)
/
/
若对任意x?A,有x ?B,则 A?B。
子集性质:
1.规定:空集是任何集合的子集:??A
2.任何集合都是自身的子集:A?A
3.子集具有可传递性 A?B, B?C? A?C;
4.子集的两种情况
思考:
(3)写出集合{a,b}的所有子集;
(4)写出集合{a,b,c}的所有子集;
(2)写出集合{a}的所有子集;
(1)写出?的所有子集.
元素个数与集合子集个数的关系:
返回
集合 集合元素的个数 集合子集个数
? 0 1
{a} 1 2
{a,b} 2 4
{a,b,c} 3 8
{a,b,c,d} 4 16
… … …
n个元素
A的子集个数为:
A的非空子集个数为:
A的真子集个数为:
A的非空真子集个数为:
元素个数与集合子集个数的关系:
思考:
请列举集合{1,2,3}的所有子集:
?,{1},{2},{3},{1,2},
{1,3}, {2,3},{1,2,3}。
二、集合相等
若两个集合的构成元素一样,则集合相等
对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素即A?B ,同时集合B的任何一个元素都是集合A的元素即: B?A ,则称集合A等于集合B,记作A=B。
即 A?B, B?A ? A=B。
三、真子集
如果集合A?B,但存在元素x∈B,且x ?A,即B至少比A多一个元素,称集合A是集合B的真子集记A B,或B A。
≠
?
≠
空集是任何非空集合的真子集
真子集具有可传递性
除A自身以外所有子集都是A的真子集
应用一:集合关系的判定
P7 练习 2
(1)a {a}; (2) {a} {a,b}
(3){a,b} {b,a};
(4){-1,1} {-1,0,1}
(5)0 ?; (6) ? {-1,1}
应用二:集合关系的证明
书上:P7 练习 3
列举法
同向简化法
应用三:集合关系求参
分类讨论!
设集合A={x|1≤x≤3},B={x|x-a≥0}
若A是B的真子集,求实数a的取值范围。
应用三:集合关系求参
1.
2.
数形结合!
知识回顾
子集定义及个数公式
集合相等
真子集
两个数学思想
复习回顾
知识回顾
集合与元素的定义
元素的性质
集合的表示
实数有相等关系、大小关系,
如5=5,5<7,5>3,等等,类比实数之间的关系,你会想到集合之间的什么关系?
思考
问:中国的区域与福建省的区域有何关系?
如果我们把福建省的区域用集合A来表示,中国区域用集合B来表示,则A在集合B内;也就是说集合A的每一个元素都在集合B内。
中央美术学院附属中学 赵巧
1.1 集 合
1.1.2 集合的关系
一、子集
对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A是集合B的子集,
读作包含于集合B,或者集合B包含集合A
当集合A不是集合B的子集,
记作A B(或B A)
记作A B(或B A)
/
/
若对任意x?A,有x ?B,则 A?B。
子集性质:
1.规定:空集是任何集合的子集:??A
2.任何集合都是自身的子集:A?A
3.子集具有可传递性 A?B, B?C? A?C;
4.子集的两种情况
思考:
(3)写出集合{a,b}的所有子集;
(4)写出集合{a,b,c}的所有子集;
(2)写出集合{a}的所有子集;
(1)写出?的所有子集.
元素个数与集合子集个数的关系:
返回
集合 集合元素的个数 集合子集个数
? 0 1
{a} 1 2
{a,b} 2 4
{a,b,c} 3 8
{a,b,c,d} 4 16
… … …
n个元素
A的子集个数为:
A的非空子集个数为:
A的真子集个数为:
A的非空真子集个数为:
元素个数与集合子集个数的关系:
思考:
请列举集合{1,2,3}的所有子集:
?,{1},{2},{3},{1,2},
{1,3}, {2,3},{1,2,3}。
二、集合相等
若两个集合的构成元素一样,则集合相等
对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素即A?B ,同时集合B的任何一个元素都是集合A的元素即: B?A ,则称集合A等于集合B,记作A=B。
即 A?B, B?A ? A=B。
三、真子集
如果集合A?B,但存在元素x∈B,且x ?A,即B至少比A多一个元素,称集合A是集合B的真子集记A B,或B A。
≠
?
≠
空集是任何非空集合的真子集
真子集具有可传递性
除A自身以外所有子集都是A的真子集
应用一:集合关系的判定
P7 练习 2
(1)a {a}; (2) {a} {a,b}
(3){a,b} {b,a};
(4){-1,1} {-1,0,1}
(5)0 ?; (6) ? {-1,1}
应用二:集合关系的证明
书上:P7 练习 3
列举法
同向简化法
应用三:集合关系求参
分类讨论!
设集合A={x|1≤x≤3},B={x|x-a≥0}
若A是B的真子集,求实数a的取值范围。
应用三:集合关系求参
1.
2.
数形结合!
知识回顾
子集定义及个数公式
集合相等
真子集
两个数学思想
