2019-2020学年人教版高一物理必修1 4.6 用牛顿运动定律解决问题(一)课后同步练习卷
文档属性
| 名称 | 2019-2020学年人教版高一物理必修1 4.6 用牛顿运动定律解决问题(一)课后同步练习卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-01 00:00:00 | ||
图片预览





文档简介
4.6 用牛顿运动定律解决问题(一)
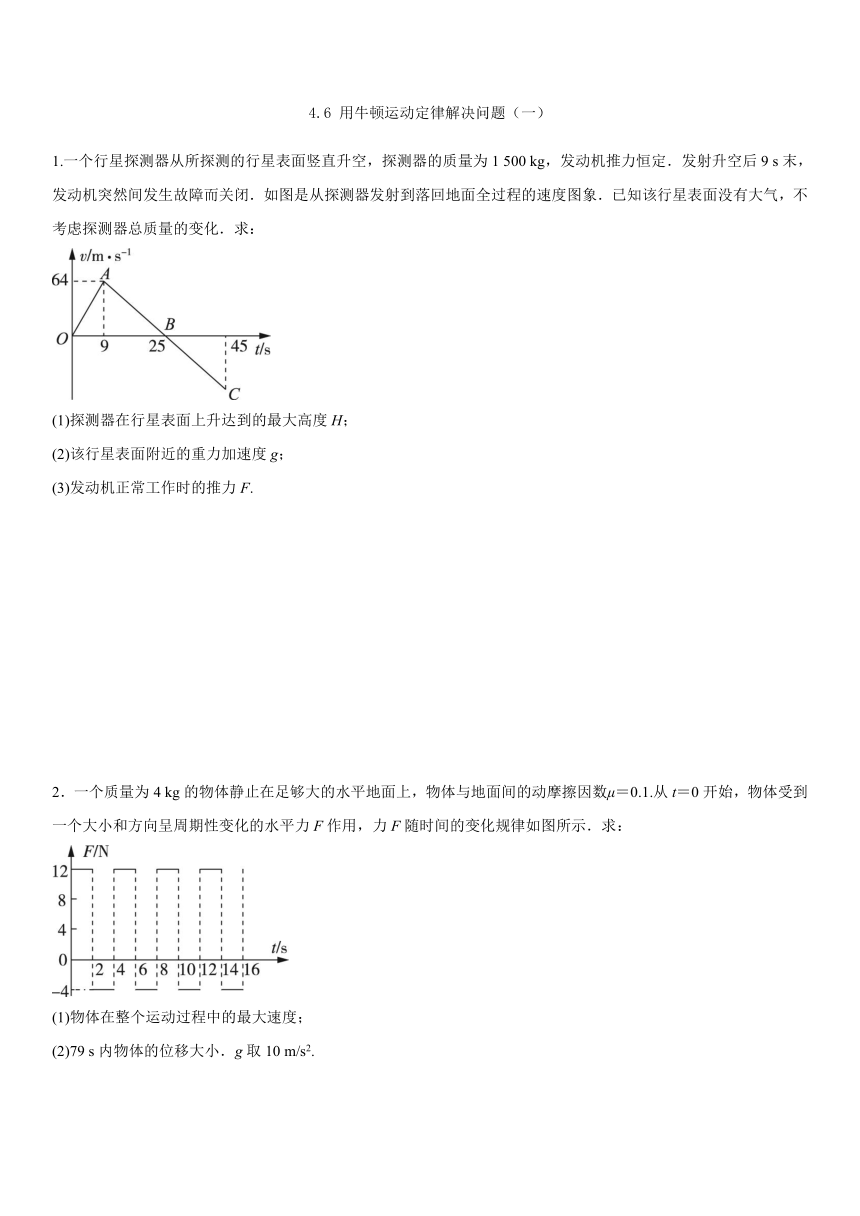
1.一个行星探测器从所探测的行星表面竖直升空,探测器的质量为1 500 kg,发动机推力恒定.发射升空后9 s末,发动机突然间发生故障而关闭.如图是从探测器发射到落回地面全过程的速度图象.已知该行星表面没有大气,不考虑探测器总质量的变化.求:
(1)探测器在行星表面上升达到的最大高度H;
(2)该行星表面附近的重力加速度g;
(3)发动机正常工作时的推力F.
2.一个质量为4 kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.求:
(1)物体在整个运动过程中的最大速度;
(2)79 s内物体的位移大小.g取10 m/s2.
3.如图所示,质量为2 kg的物体在40 N水平推力作用下,从静止开始1 s内沿足够长的竖直墙壁下滑3 m.求:(取g=10 m/s2)
(1)物体运动的加速度大小;
(2)物体受到的摩擦力大小;
(3)物体与墙壁间的动摩擦因数.
4.某研究性学习小组利用力传感器研究小球与竖直挡板间的作用力,实验装置如图4所示,已知斜面倾角为45°,光滑小球的质量m=3 kg,力传感器固定在竖直挡板上.求:(g=10 m/s2)
(1)当整个装置静止时,力传感器的示数;
(2)当整个装置向右做匀加速直线运动时,力传感器示数为36 N,此时装置的加速度大小;
(3)某次整个装置在水平方向做匀加速直线运动时,力传感器示数恰好为0,此时整个装置的运动方向如何?加速度为多大?
5如图所示,总质量为m的滑雪者以初速度v0沿倾角为θ的斜面向上自由滑行,雪橇与斜面间动摩擦因数为μ,重力加速度为g,假设斜面足够长.不计空气阻力.试求:
(1)滑雪者沿斜面上滑的加速度大小;
(2)滑雪者沿斜面上滑的最大距离;
(3)若滑雪者滑至最高点后掉转方向向下自由滑行,求沿斜面自由下滑的加速度大小.
6.质量为2 kg的小球,以30 m/s的速度竖直向上抛出,经过2.5 s到达最高点(g=10 m/s2),求:
(1)小球在上升过程中受到空气的平均阻力;
(2)小球上升的最大高度;
(3)若小球在空气中的阻力大小不变,小球落回到抛出点的速度.
7.如图所示,放置于水平地面质量是10 kg 的物体,在与水平方向成37°角的斜向右上方的拉力F=100 N的作用下,由静止开始沿水平地面做直线运动,物体与地面间的动摩擦因数μ=0.5(sin37°=0.6,cos37°=0.8,g=10 m/s2),试求:
(1)5 s末物体的速度大小和5 s内物体的位移大小;
(2)拉力F多大时物体可以做匀速直线运动?
8.放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系如图1所示,物块速度v与时间t的关系如图2所示(g=10 m/s2).求:
(1)物块的质量m;
(2)物块与地面之间的动摩擦因数μ;
(3)撤去推力后物体还能滑行多远.
9.如图所示,一固定足够长的粗糙斜面与水平面夹角θ=30°.一个质量m=1 kg的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数μ= .g取10 m/s2.则:
(1)求物体在拉力F作用下运动的加速度大小a1;
(2)若力F作用1.2 s后撤去,求物体在上滑过程中距出发点的最大距离.
10.质量m=1 kg的物体置于倾角θ=37°的足够长固定斜面上,对物体施加平行于斜面向上的恒力F,作用时间t1=1 s后撤去恒力,物体运动的部分v?t图象如图乙所示,取g=10 m/s2,试求:
(1)物体沿斜面上滑过程中的两个加速度;
(2)恒力F的大小和斜面与物体间的动摩擦因数μ;
(3)物体t=4 s时的速度v.
参考答案
1.一个行星探测器从所探测的行星表面竖直升空,探测器的质量为1 500 kg,发动机推力恒定.发射升空后9 s末,发动机突然间发生故障而关闭.如图是从探测器发射到落回地面全过程的速度图象.已知该行星表面没有大气,不考虑探测器总质量的变化.求:
(1)探测器在行星表面上升达到的最大高度H;
(2)该行星表面附近的重力加速度g;
(3)发动机正常工作时的推力F.
【答案】(1)800 m (2)4 m/s2 (3)1.67×104 N
【解析】(1)0~25 s内探测器一直处于上升阶段,上升的最大高度在数值上等于△OAB的面积,即H=×25×64 m=800 m.
(2)9 s末发动机关闭,此后探测器只受重力作用,故在这一阶段的加速度即为该行星表面的重力加速度,由图象得重力加速度g==4 m/s2.
(3)由图象知探测器加速上升阶段探测器的加速度为a= m/s2,根据牛顿运动定律,得F-mg=ma,所以发动机正常工作时的推力F=m(g+a)≈1.67×104 N.
2.一个质量为4 kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.求:
(1)物体在整个运动过程中的最大速度;
(2)79 s内物体的位移大小.g取10 m/s2.
【答案】(1)4 m/s (2)159 m
【解析】由力F随时间的变化规律图和牛顿第二定律可求出物体在前半周期和后半周期的加速度,进而判断物体的运动状态,然后根据速度时间公式求出物体在整个运动过程中的最大速度;由力F随时间的变化规律图可知,力的变化具有周期性,周期为4 s,可以根据牛顿第二定律求出一个周期内的位移,79 s为20个周期少1 s,我们可以算出80 s内的总位移再减去最后1 s的位移,即为79 s内的位移.
(1)当物体在前半周期时由牛顿第二定律,得F1-μmg=ma1,解得a1=2 m/s2
在前半周期做匀加速运动,当物体在后半周期内,由牛顿第二定律,得F2+μmg=ma2,解得a2=2 m/s2
在后半周期内做匀减速运动,在2 s末的速度最大,最大速度为v=at=4 m/s.
(2)前半周期和后半周期位移相等:s1=a1t2=4 m
解得t=2 s
所以物体每4 s的运动情况相同,物体每4 s(即一个周期)的位移为s=2s1=8 m,
考虑第80 s物体运动情况:
第80 s初、即79 s末的速度v=a2×=2 m/s
第80 s的位移s0=×=1 m
所以79 s内物体的位移大小为s2=20s-s0=159 m.
3.如图所示,质量为2 kg的物体在40 N水平推力作用下,从静止开始1 s内沿足够长的竖直墙壁下滑3 m.求:(取g=10 m/s2)
(1)物体运动的加速度大小;
(2)物体受到的摩擦力大小;
(3)物体与墙壁间的动摩擦因数.
【答案】 (1)6 m/s2 (2)8 N (3)0.2
【解析】 (1)由h=at2,可得:a==6 m/s2
(2)分析物体受力情况如图所示:
水平方向:物体所受合外力为零,FN=F=40 N
竖直方向:取向下为正方向,由牛顿第二定律得:mg-Ff=ma
可得:Ff=mg-ma=8 N
(3)物体与墙壁间的滑动摩擦力Ff=μFN
所以μ===0.2.
4.某研究性学习小组利用力传感器研究小球与竖直挡板间的作用力,实验装置如图4所示,已知斜面倾角为45°,光滑小球的质量m=3 kg,力传感器固定在竖直挡板上.求:(g=10 m/s2)
(1)当整个装置静止时,力传感器的示数;
(2)当整个装置向右做匀加速直线运动时,力传感器示数为36 N,此时装置的加速度大小;
(3)某次整个装置在水平方向做匀加速直线运动时,力传感器示数恰好为0,此时整个装置的运动方向如何?加速度为多大?
【答案】 (1)30 N (2)2 m/s2 (3)方向向左,加速度大小为10 m/s2
【解析】 (1)以小球为研究对象,设小球与力传感器静止时的作用力大小为F,小球与斜面间的作用力大小为FN,对小球受力分析如图所示,由几何关系可知:
F=mg=3×10 N=30 N;
(2)竖直方向FNcos 45°=mg;
水平方向F′-FNsin 45°=ma;
解得:a=2 m/s2;
(3)要使力传感器示数为0,则有:
FNcos 45°=mg;FNsin 45°=ma′;
解得:a′=10 m/s2,方向向左.
5.如图所示,总质量为m的滑雪者以初速度v0沿倾角为θ的斜面向上自由滑行,雪橇与斜面间动摩擦因数为μ,重力加速度为g,假设斜面足够长.不计空气阻力.试求:
(1)滑雪者沿斜面上滑的加速度大小;
(2)滑雪者沿斜面上滑的最大距离;
(3)若滑雪者滑至最高点后掉转方向向下自由滑行,求沿斜面自由下滑的加速度大小.
【答案】 (1)g(sinθ+μcosθ) (2)v/2g(sinθ+μcosθ) (3)g(sinθ-μcosθ)
【解析】 (1)对滑雪者进行受力分析得
N=mgcosθ
f+mgsinθ=ma1
f=μN
求得a1=g(sinθ+μcosθ).
(2)由运动公式:v=2a1x
x=.
(3)根据牛顿第二定律:mgsinθ-μmgcosθ=ma2
求得a2=g(sinθ-μcosθ).
6质量为2 kg的小球,以30 m/s的速度竖直向上抛出,经过2.5 s到达最高点(g=10 m/s2),求:
(1)小球在上升过程中受到空气的平均阻力;
(2)小球上升的最大高度;
(3)若小球在空气中的阻力大小不变,小球落回到抛出点的速度.
【答案】(1)4 N 方向竖直向下 (2)37.5 m(3)24.5 m/s 方向竖直向下
【解析】(1)以初速度方向为正方向,由速度公式v=v0+a1t得,小球上升时的加速度a1==-12 m/s2.
根据牛顿第二定律知ma1=-mg+F
所以阻力F=ma1+mg=-4 N
负号表示阻力方向竖直向下.
(2)根据推论公式-v=2a1h
小球上升的最大高度
h=-=37.5 m.
(3)小球下落时的合力大小F合=mg+F
根据牛顿第二定律,小球下落时的加速度大小a2==8 m/s2.
根据公式v2=2a2h.
小球落回到抛出点的速度大小.
v== m/s≈24.5 m/s
速度方向竖直向下.
7.如图所示,放置于水平地面质量是10 kg 的物体,在与水平方向成37°角的斜向右上方的拉力F=100 N的作用下,由静止开始沿水平地面做直线运动,物体与地面间的动摩擦因数μ=0.5(sin37°=0.6,cos37°=0.8,g=10 m/s2),试求:
(1)5 s末物体的速度大小和5 s内物体的位移大小;
(2)拉力F多大时物体可以做匀速直线运动?
【答案】(1)30 m/s 75 m (2)45.5 N
【解析】(1)分析物体的受力情况,如图所示:
x轴方向上,Fcos37°-Ff=ma.
y轴方向上,Fsin37°+FN=mg.
其中Ff=μFN.联立解得
a=6 m/s2.
5 s末物体的速度大小
v=at=30 m/s.
5 s内物体通过的位移
x=at2=75 m.
(2)物体做匀速运动时加速度为零,Fcos37°-μ(mg-Fsin37°)=0.
解得F≈45.5 N
8.放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系如图1所示,物块速度v与时间t的关系如图2所示(g=10 m/s2).求:
(1)物块的质量m;
(2)物块与地面之间的动摩擦因数μ;
(3)撤去推力后物体还能滑行多远.
【答案】(1)0.5 kg (2)0.4 (3)2 m
【解析】(1)分析图象可知,4~6 s时间内物体做匀速直线运动,推力等于摩擦力,f=F3=2 N.
2~4 s时间内,水平推力F=3 N,
物体加速度a==2 m/s2.
根据牛顿第二定律得F-f=ma.
代入数据解得m=0.5 kg.
(2)根据滑动摩擦力公式可知,f=μmg,解得μ=0.4.
(3)撤去推力后,物体只受摩擦力作用,加速度a′=μg,根据运动学公式可知,滑行距离x=.
联立解得x=2 m.
9.如图所示,一固定足够长的粗糙斜面与水平面夹角θ=30°.一个质量m=1 kg的小物体(可视为质点),在F=10 N的沿斜面向上的拉力作用下,由静止开始沿斜面向上运动.已知斜面与物体间的动摩擦因数μ= .g取10 m/s2.则:
(1)求物体在拉力F作用下运动的加速度大小a1;
(2)若力F作用1.2 s后撤去,求物体在上滑过程中距出发点的最大距离.
【答案】 (1)2.5 m/s2 (2)2.4 m
【解析】 (1)对物体受力分析,根据牛顿第二定律:
物体受到斜面对它的支持力FN=mgcos θ=5 N,
物体的加速度a1==2.5 m/s2.
(2)力F作用t0=1.2 s后,速度大小为v=a1t0=3 m/s,物体向上滑动的距离x1=a1t02=1.8 m.
此后它将向上匀减速运动,其加速度大小a2==7.5 m/s2.
这一过程物体向上滑动的距离x2==0.6 m.
整个上滑过程移动的最大距离x=x1+x2=2.4 m.
10.质量m=1 kg的物体置于倾角θ=37°的足够长固定斜面上,对物体施加平行于斜面向上的恒力F,作用时间t1=1 s后撤去恒力,物体运动的部分v?t图象如图乙所示,取g=10 m/s2,试求:
(1)物体沿斜面上滑过程中的两个加速度;
(2)恒力F的大小和斜面与物体间的动摩擦因数μ;
(3)物体t=4 s时的速度v.
【答案】 (1)20 m/s2 -10 m/s2 (2)30 N 0.5 (3)2 m/s,方向沿斜面向下
【解析】 (1)根据v?t图象可知,加速阶段加速度为a1== m/s2=20 m/s2,
减速阶段加速度a2= m/s2=-10 m/s2.
(2)根据牛顿第二定律可知,
加速上升过程 F-mgsinθ-μmgcosθ=ma1
减速上升过程-mgsinθ-μmgcosθ=ma2
联立解得 F=30 N,μ=0.5.
(3)由题意可知,mgsinθ=6 N>μmgcosθ=4 N,可知物体减速为零后可以匀加速下滑,又1 s后物体做匀减速,3 s末的速度为v3=v1+at=20+(-10)×2 m/s=0 m/s,
即3 s末速度为零,则3 s到4 s这1 s的时间间隔内物体沿斜面向下做匀加速直线运动,设加速度为a3,由牛顿第二定律得mgsinθ-μmgcosθ=ma3
解得a3=2 m/s2
由速度时间关系可知,4 s时速度v4=v3+at=0+2×1 m/s=2 m/s,方向沿斜面向下.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
