高中数学人教版必修1课件:1.2.1函数概念(共30张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:1.2.1函数概念(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 862.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 17:37:20 | ||
图片预览











文档简介
(共30张PPT)
函数的概念
温故
设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有惟一的值与它对应,则称x是自变量,y是x的函数
1、初中学习的函数概念是什么?
温故
2、请问:我们在初中学过哪些函数?
温故
显然,仅用初中函数的概念很难回答这些问题。因此,需要从新的高度认识函数。
是函数吗?
是同一函数吗?
与
3、利用初中函数定义能解决下列问题:
P15
新知I:函数的定义
归纳以上三个实例,我们看到,三个实例中变量之间的关系可以描述为:
对于数集A中的每一个x,按照某种对应关系f,在数集B中都有惟一确定的y和它对应,记作 f: A→B.
注:这种对应关系的表示具有多样性,如:表达式、图象、表格
新知I:函数的定义
设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数,记作 y=f(x) , x∈A 。
其中:x叫做自变量, x构成的集合A叫做函数的定义域
与x的值相对应的y的值叫做函数值,如f(a),
函数值的集合{f(x)|x∈A}={y|y=f(x),x∈A} 叫做函数的值域。
注:函数符号y=f(x)表示“y是x的函数”而不是表示“y等于f与x的乘积,所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示
习惯上我们仍称y是x的函数
定义域和值域与集合A和B之间分别是什么关系?
新知I:函数的定义
判断下列对应能否表示y是x的函数
(1) y=|x| (2)|y|=x
(3) y=x 2 (4)y2 =x
(5) y2+x2=1 (6)y2-x2=1
(1)能
(2)不能
(5)不能
(3)能
(4)不能
(6)不能
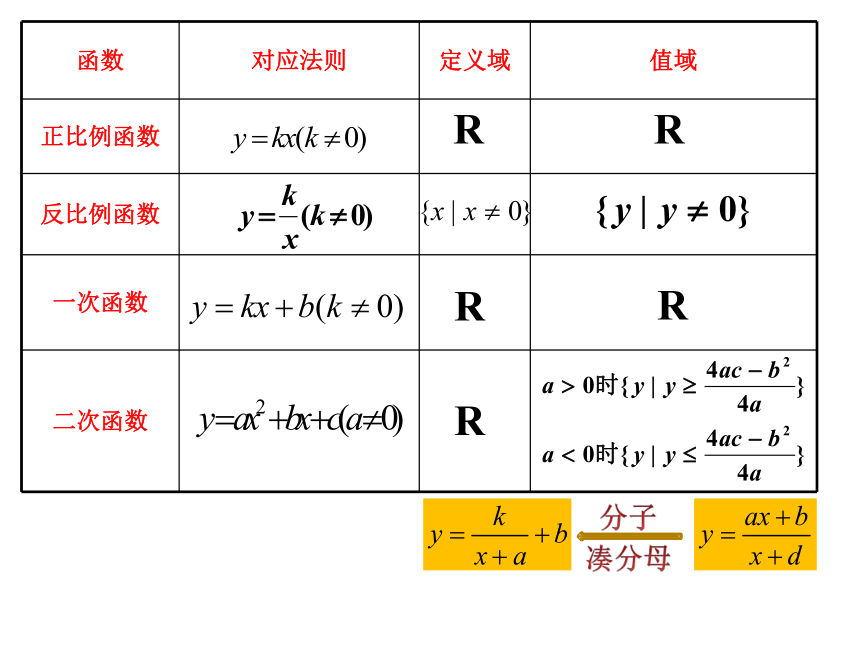
分子
凑分母
函数 对应法则 定义域 值域
正比例函数
反比例函数
一次函数
二次函数
R
R
R
R
R
新知II:同一函数
① 定义域、值域、对应关系是决定函数的三要素,是一个整体;故两个函数的三要素一样,则两个函数是相同的!
② 有些函数不明确说明定义域,则定义域就是使函数有意义的自变量的取值范围;
③ 显然值域不一定等于B,它可以由定义域、对应法则惟一确定,所以如果两个函数 定义域相同,并且对应关系本质相同,则它们的三要素一定都一样,我们就称这它们为同一函数
新知II:同一函数
下列函数中哪个与函数y=x是同一个函数?
【例】
是否为函数?
f(x)=x2 与 f(t)=t2 是否为同一函数 ?
思考:
1.
2.
新知II:同一函数
练习:
判断下列函数f(x)与g(x)是否表示同一个函数,并说明理由?
小秘方
基本函数(9) 分段函数 组合函数 复合函数
新知III:求函数定义域(具体)
使各部分式子都有意义的实数的集合(即各集合的交集)
(3)
(4)y=f (x)是由几个部分的式子构成的即组合函数,则定义域是
(1)如果y=f (x)是整式,则定义域是
(2)如果y=f (x)/g(x)分式,则定义域是{x|g(x)≠0}
(5) y=f (x)是分段函数,
全体实数(R)
分段中各段集合求并
(6) 实际问题求函数,
求实际问题出发决定定义域
分段求并组合求交
新知III:求函数定义域(具体)
设a,b是两个实数,而且a(1)、满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为 [a,b]
(2)、满足不等式a(3)、满足不等式a≤x区间的概念
这里的实数a与b都叫做相应区间的端点。
→集合表示的第五种和最鼓励的方法!
新知III:求函数定义域(具体)
求下列函数的定义域:
已知y=f(x),给出对应法则:y=x2-x,
1)输入
那么输出的值分别为x:
2)能输入”x+1”这样的式子吗?
函数值
新函数
复合函数: 定义域:x ,值域:y
新知III:求函数定义域(抽象)
新知III:求函数定义域(抽象)
若函数 的定义域为[1,3],则函数 的定义域为:
若函数 的定义域为[1,3],则函数 的定义域为:
新知IV:简单函数求值和求值域
已知y=f(x),给出对应法则:y=x2-x,
1)输入
那么输出的值分别为x:
2)能输入”x+1”这样的式子吗?
函数值
新函数
复合函数: 定义域:x ,值域:y
新知IV:简单函数求值和求值域
y=f(x),给出对应法则:y=x2-x,
分别定义域为[-3,3]、 [0,3]、 [1,4]时相应的函数 值域
→1.基本函数:画图,找横再找纵
y=f(x),给出对应法则:y=x4-x2,
分别定义域为R、 [0,3] 时相应的函数 值域
→ 2.复合函数:换元法,设t则y再画图
→ 3. 不等式穿衣服求值域
?
补充练习:
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
小结
1、函数的定义及概念
2、函数的三要素
定义域
函数值构成的值域
对应法则
自变量的取值范围 (具体和抽象)
解析式、
图象、表格
将x的取值代入得函数值,
三种方法求值域
解析式定方法
定义域定答案
一空十分,共100分
函数的概念
温故
设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有惟一的值与它对应,则称x是自变量,y是x的函数
1、初中学习的函数概念是什么?
温故
2、请问:我们在初中学过哪些函数?
温故
显然,仅用初中函数的概念很难回答这些问题。因此,需要从新的高度认识函数。
是函数吗?
是同一函数吗?
与
3、利用初中函数定义能解决下列问题:
P15
新知I:函数的定义
归纳以上三个实例,我们看到,三个实例中变量之间的关系可以描述为:
对于数集A中的每一个x,按照某种对应关系f,在数集B中都有惟一确定的y和它对应,记作 f: A→B.
注:这种对应关系的表示具有多样性,如:表达式、图象、表格
新知I:函数的定义
设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数,记作 y=f(x) , x∈A 。
其中:x叫做自变量, x构成的集合A叫做函数的定义域
与x的值相对应的y的值叫做函数值,如f(a),
函数值的集合{f(x)|x∈A}={y|y=f(x),x∈A} 叫做函数的值域。
注:函数符号y=f(x)表示“y是x的函数”而不是表示“y等于f与x的乘积,所以若对应关系用g、 G、F 等表示,则函数就可用g(x)、F(x)、G(x)等 表示
习惯上我们仍称y是x的函数
定义域和值域与集合A和B之间分别是什么关系?
新知I:函数的定义
判断下列对应能否表示y是x的函数
(1) y=|x| (2)|y|=x
(3) y=x 2 (4)y2 =x
(5) y2+x2=1 (6)y2-x2=1
(1)能
(2)不能
(5)不能
(3)能
(4)不能
(6)不能
分子
凑分母
函数 对应法则 定义域 值域
正比例函数
反比例函数
一次函数
二次函数
R
R
R
R
R
新知II:同一函数
① 定义域、值域、对应关系是决定函数的三要素,是一个整体;故两个函数的三要素一样,则两个函数是相同的!
② 有些函数不明确说明定义域,则定义域就是使函数有意义的自变量的取值范围;
③ 显然值域不一定等于B,它可以由定义域、对应法则惟一确定,所以如果两个函数 定义域相同,并且对应关系本质相同,则它们的三要素一定都一样,我们就称这它们为同一函数
新知II:同一函数
下列函数中哪个与函数y=x是同一个函数?
【例】
是否为函数?
f(x)=x2 与 f(t)=t2 是否为同一函数 ?
思考:
1.
2.
新知II:同一函数
练习:
判断下列函数f(x)与g(x)是否表示同一个函数,并说明理由?
小秘方
基本函数(9) 分段函数 组合函数 复合函数
新知III:求函数定义域(具体)
使各部分式子都有意义的实数的集合(即各集合的交集)
(3)
(4)y=f (x)是由几个部分的式子构成的即组合函数,则定义域是
(1)如果y=f (x)是整式,则定义域是
(2)如果y=f (x)/g(x)分式,则定义域是{x|g(x)≠0}
(5) y=f (x)是分段函数,
全体实数(R)
分段中各段集合求并
(6) 实际问题求函数,
求实际问题出发决定定义域
分段求并组合求交
新知III:求函数定义域(具体)
设a,b是两个实数,而且a
(2)、满足不等式a
这里的实数a与b都叫做相应区间的端点。
→集合表示的第五种和最鼓励的方法!
新知III:求函数定义域(具体)
求下列函数的定义域:
已知y=f(x),给出对应法则:y=x2-x,
1)输入
那么输出的值分别为x:
2)能输入”x+1”这样的式子吗?
函数值
新函数
复合函数: 定义域:x ,值域:y
新知III:求函数定义域(抽象)
新知III:求函数定义域(抽象)
若函数 的定义域为[1,3],则函数 的定义域为:
若函数 的定义域为[1,3],则函数 的定义域为:
新知IV:简单函数求值和求值域
已知y=f(x),给出对应法则:y=x2-x,
1)输入
那么输出的值分别为x:
2)能输入”x+1”这样的式子吗?
函数值
新函数
复合函数: 定义域:x ,值域:y
新知IV:简单函数求值和求值域
y=f(x),给出对应法则:y=x2-x,
分别定义域为[-3,3]、 [0,3]、 [1,4]时相应的函数 值域
→1.基本函数:画图,找横再找纵
y=f(x),给出对应法则:y=x4-x2,
分别定义域为R、 [0,3] 时相应的函数 值域
→ 2.复合函数:换元法,设t则y再画图
→ 3. 不等式穿衣服求值域
?
补充练习:
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
新知IV:简单函数求值和求值域
小结
1、函数的定义及概念
2、函数的三要素
定义域
函数值构成的值域
对应法则
自变量的取值范围 (具体和抽象)
解析式、
图象、表格
将x的取值代入得函数值,
三种方法求值域
解析式定方法
定义域定答案
一空十分,共100分
