24.2.4 圆的确定(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.2.4 圆的确定(基础达标+巩固提升+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 09:01:23 | ||
图片预览



文档简介
沪科版数学九年级下册同步课时训练
第24章 圆
24.2 圆的基本性质
第4课时 圆的确定
要点测评 基础达标
要点1 确定圆的条件
1. 下列命题正确的个数有( )
①过两点可以作无数个圆,②经过三点一定可以作圆,③任意一个三角形有一个外接圆,而且只有一个外接圆,④任意一个圆有且只有一个内接三角形.
A. 1个 B. 2个 C. 3个 D. 4个
2. 小明家的房前有一块空地,空地上有三棵树A,B,C,如图所示,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
要点2 反证法
3. 用“反证法”证明命题“等腰三角形的底角是锐角”时,是先假设 .
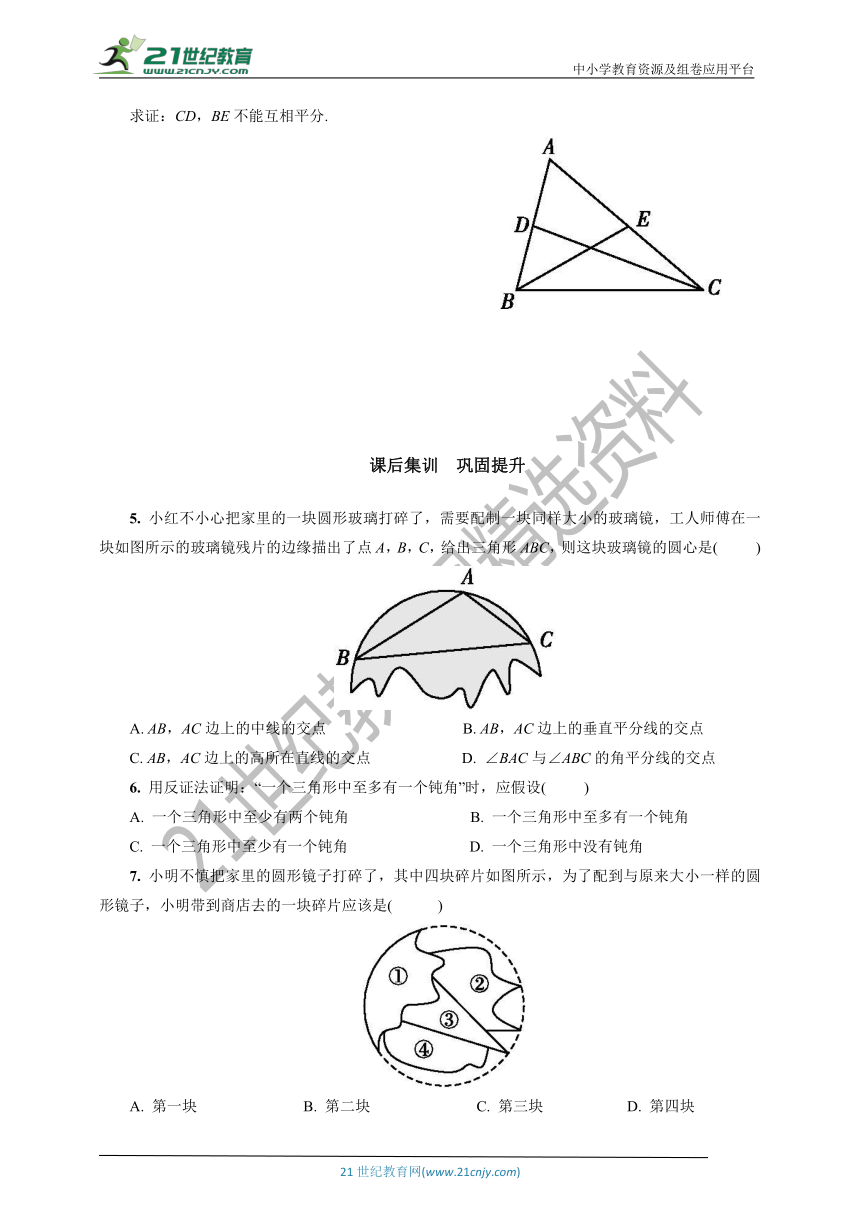
4. 如图所示,已知D,E是△ABC的边AB,AC上的点,连接CD,BE.
求证:CD,BE不能互相平分.
课后集训 巩固提升
5. 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A. AB,AC边上的中线的交点 B. AB,AC边上的垂直平分线的交点
C. AB,AC边上的高所在直线的交点 D. ∠BAC与∠ABC的角平分线的交点
6. 用反证法证明:“一个三角形中至多有一个钝角”时,应假设( )
A. 一个三角形中至少有两个钝角 B. 一个三角形中至多有一个钝角
C. 一个三角形中至少有一个钝角 D. 一个三角形中没有钝角
7. 小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A. 第一块 B. 第二块 C. 第三块 D. 第四块
8. 小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. 2 cm B. 4 cm C. 6 cm D. 8 cm
9. 用反证法证明“过同一直线上的三点不能作圆”,应先假设 .
10. 平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4),则△ABC的外接圆的圆心坐标为 ,△ABC的外接圆在x轴上所截的弦长为 .
11. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,则△ABC的面积为 .
12. 用反证法证明:一个三角形中不能有两个直角.
13. 根据三角形外心的概念,我们可引入一个新定义:
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A=90°,BC=10,AB=6,如果准外心P在AC边上,求PA的长.
14. 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.∠DBC=∠CAD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
参 考 答 案
1. B 【解析】过两点可以作无数个圆,故①正确;经过不在同一直线上的三点可以确定一个圆,故②错误;任意一个三角形都有外接圆,而且只有一个外接圆,故③正确;任意一个圆都有无数个内接三角形,故④错误.正确的有2个,故选B.
2. 解:(1)用尺规作出两边的垂直平分线,设两条垂直平分线的交点为O,以点O为圆心,OA为半径作出☉O,☉O即为所求作的花坛的位置,如图所示.
(2)因为∠BAC=90°,AB=8米,AC=6米,所以BC=10米.所以△ABC外接圆的半径为5米.所以小明家圆形花坛的面积为25π平方米.
3. 等腰三角形的两底角都是直角或钝角 【解析】根据反证法的第一步:假设结论不成立,可以假设“等腰三角形的两底角都是直角或钝角”.
4. 证明:连接DE.假设CD,BE互相平分.那么四边形BCED是平行四边形.所以DE∥BC,AB∥AC,这与已知AB,AC交于A相矛盾,所以CD,BE不能互相平分.
5. B 【解析】本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B.
6. A 【解析】根据反证法就是从结论的反面出发进行假设,所以证明“一个三角形中至多有一个钝角”,应假设:一个三角形中至少有两个钝角.故选A.
7. A 【解析】第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选A.
8. B 【解析】过点A作BC边上的垂线交BC于点D,过点B作AC边上的垂线交AD于点O,则O为圆心.设☉O的半径为R,由等边三角形的性质知:∠OBD=30°,OB=R.所以BD=cos ∠OBD×OB=R,BC=2BD=R.因为BC=12 cm,所以R=4 cm,故选B.
9. 过同一直线上的三点能作圆
10. (-2,-1) 4 【解析】因为B(-6,-4),C(2,-4),所以线段BC的垂直平分线是x=-2,因为A(2,2),C(2,-4),所以线段AC的垂直平分线是y=-1,所以△ABC的外接圆的圆心M的坐标为(-2,-1);由题意得AC=6,BC=8,由勾股定理得AB=10.连接DM,作MN⊥DE于N,由题意可知DM=5,MN=1,则DN=2,所以DE=4.
11. 8-4或8+4 【解析】由题意可得,当△ABC为△A1BC时,连接OB,OC,因为点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,OB=OC,所以△OBC为等边三角形,OB=OC=BC=4,OA1⊥BC于点D,所以CD=2,所以OD=2,所以A1D=4-2,所以△ABC的面积=×4×(4-2)=8-4,当△ABC为△A2BC时,连接OB,OC,A2D=4+2.同理可得,△ABC的面积为8+4.
12. 解:已知:△ABC,
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角为直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°.这与三角形的内角和定理相矛盾,所以∠A=∠B=90°不成立.因此一个三角形中不能有两个角是直角.
13. 解:在Rt△ABC中,因为∠A=90°,BC=10,AB=6,所以AC===8,若PB=PC,连接PB,设PA=x,则PB=PC=8-x,在Rt△PAB中,因为PB2=AP2+AB2,所以(8-x)2=x2+62,所以x=,即PA=.若PA=PC,则PA=4.若PA=PB,由图知,在Rt△PAB中,不可能.故PA的长是4或.
14. (1)证明:因为AD为直径,AD⊥BC,所以由垂径定理得:=,所以根据圆心角、弧、弦之间的关系得:BD=CD.
(2)解:B,E,C三点在以D为圆心,以DB为半径的圆上.理由:由垂径定理可得:∠AFB=∠AFC=90°,BF=FC,又因为AF=AF,所以△AFB≌△AFC,所以∠1=∠2,因为∠2=∠3,所以∠1=∠3,又∠DBE=∠3+∠4,∠DEB=∠1+∠5,因为BE是∠ABC的平分线,所以∠4=∠5,所以∠DBE=∠DEB,所以DB=DE.由(1)知:BD=CD,所以DB=DE=DC.所以B,E,C三点在以D为圆心,以DB为半径的圆上.
第24章 圆
24.2 圆的基本性质
第4课时 圆的确定
要点测评 基础达标
要点1 确定圆的条件
1. 下列命题正确的个数有( )
①过两点可以作无数个圆,②经过三点一定可以作圆,③任意一个三角形有一个外接圆,而且只有一个外接圆,④任意一个圆有且只有一个内接三角形.
A. 1个 B. 2个 C. 3个 D. 4个
2. 小明家的房前有一块空地,空地上有三棵树A,B,C,如图所示,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
要点2 反证法
3. 用“反证法”证明命题“等腰三角形的底角是锐角”时,是先假设 .
4. 如图所示,已知D,E是△ABC的边AB,AC上的点,连接CD,BE.
求证:CD,BE不能互相平分.
课后集训 巩固提升
5. 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A. AB,AC边上的中线的交点 B. AB,AC边上的垂直平分线的交点
C. AB,AC边上的高所在直线的交点 D. ∠BAC与∠ABC的角平分线的交点
6. 用反证法证明:“一个三角形中至多有一个钝角”时,应假设( )
A. 一个三角形中至少有两个钝角 B. 一个三角形中至多有一个钝角
C. 一个三角形中至少有一个钝角 D. 一个三角形中没有钝角
7. 小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A. 第一块 B. 第二块 C. 第三块 D. 第四块
8. 小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A. 2 cm B. 4 cm C. 6 cm D. 8 cm
9. 用反证法证明“过同一直线上的三点不能作圆”,应先假设 .
10. 平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4),则△ABC的外接圆的圆心坐标为 ,△ABC的外接圆在x轴上所截的弦长为 .
11. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,则△ABC的面积为 .
12. 用反证法证明:一个三角形中不能有两个直角.
13. 根据三角形外心的概念,我们可引入一个新定义:
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠A=90°,BC=10,AB=6,如果准外心P在AC边上,求PA的长.
14. 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.∠DBC=∠CAD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
参 考 答 案
1. B 【解析】过两点可以作无数个圆,故①正确;经过不在同一直线上的三点可以确定一个圆,故②错误;任意一个三角形都有外接圆,而且只有一个外接圆,故③正确;任意一个圆都有无数个内接三角形,故④错误.正确的有2个,故选B.
2. 解:(1)用尺规作出两边的垂直平分线,设两条垂直平分线的交点为O,以点O为圆心,OA为半径作出☉O,☉O即为所求作的花坛的位置,如图所示.
(2)因为∠BAC=90°,AB=8米,AC=6米,所以BC=10米.所以△ABC外接圆的半径为5米.所以小明家圆形花坛的面积为25π平方米.
3. 等腰三角形的两底角都是直角或钝角 【解析】根据反证法的第一步:假设结论不成立,可以假设“等腰三角形的两底角都是直角或钝角”.
4. 证明:连接DE.假设CD,BE互相平分.那么四边形BCED是平行四边形.所以DE∥BC,AB∥AC,这与已知AB,AC交于A相矛盾,所以CD,BE不能互相平分.
5. B 【解析】本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B.
6. A 【解析】根据反证法就是从结论的反面出发进行假设,所以证明“一个三角形中至多有一个钝角”,应假设:一个三角形中至少有两个钝角.故选A.
7. A 【解析】第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选A.
8. B 【解析】过点A作BC边上的垂线交BC于点D,过点B作AC边上的垂线交AD于点O,则O为圆心.设☉O的半径为R,由等边三角形的性质知:∠OBD=30°,OB=R.所以BD=cos ∠OBD×OB=R,BC=2BD=R.因为BC=12 cm,所以R=4 cm,故选B.
9. 过同一直线上的三点能作圆
10. (-2,-1) 4 【解析】因为B(-6,-4),C(2,-4),所以线段BC的垂直平分线是x=-2,因为A(2,2),C(2,-4),所以线段AC的垂直平分线是y=-1,所以△ABC的外接圆的圆心M的坐标为(-2,-1);由题意得AC=6,BC=8,由勾股定理得AB=10.连接DM,作MN⊥DE于N,由题意可知DM=5,MN=1,则DN=2,所以DE=4.
11. 8-4或8+4 【解析】由题意可得,当△ABC为△A1BC时,连接OB,OC,因为点O是等腰△ABC的外心,且∠BOC=60°,底边BC=4,OB=OC,所以△OBC为等边三角形,OB=OC=BC=4,OA1⊥BC于点D,所以CD=2,所以OD=2,所以A1D=4-2,所以△ABC的面积=×4×(4-2)=8-4,当△ABC为△A2BC时,连接OB,OC,A2D=4+2.同理可得,△ABC的面积为8+4.
12. 解:已知:△ABC,
求证:∠A,∠B,∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角为直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°.这与三角形的内角和定理相矛盾,所以∠A=∠B=90°不成立.因此一个三角形中不能有两个角是直角.
13. 解:在Rt△ABC中,因为∠A=90°,BC=10,AB=6,所以AC===8,若PB=PC,连接PB,设PA=x,则PB=PC=8-x,在Rt△PAB中,因为PB2=AP2+AB2,所以(8-x)2=x2+62,所以x=,即PA=.若PA=PC,则PA=4.若PA=PB,由图知,在Rt△PAB中,不可能.故PA的长是4或.
14. (1)证明:因为AD为直径,AD⊥BC,所以由垂径定理得:=,所以根据圆心角、弧、弦之间的关系得:BD=CD.
(2)解:B,E,C三点在以D为圆心,以DB为半径的圆上.理由:由垂径定理可得:∠AFB=∠AFC=90°,BF=FC,又因为AF=AF,所以△AFB≌△AFC,所以∠1=∠2,因为∠2=∠3,所以∠1=∠3,又∠DBE=∠3+∠4,∠DEB=∠1+∠5,因为BE是∠ABC的平分线,所以∠4=∠5,所以∠DBE=∠DEB,所以DB=DE.由(1)知:BD=CD,所以DB=DE=DC.所以B,E,C三点在以D为圆心,以DB为半径的圆上.
