人教版必修一 2.1 实验:探究小车速度随时间变化的规律(共29张PPT)
文档属性
| 名称 | 人教版必修一 2.1 实验:探究小车速度随时间变化的规律(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-02 06:12:53 | ||
图片预览



文档简介
(共30张PPT)
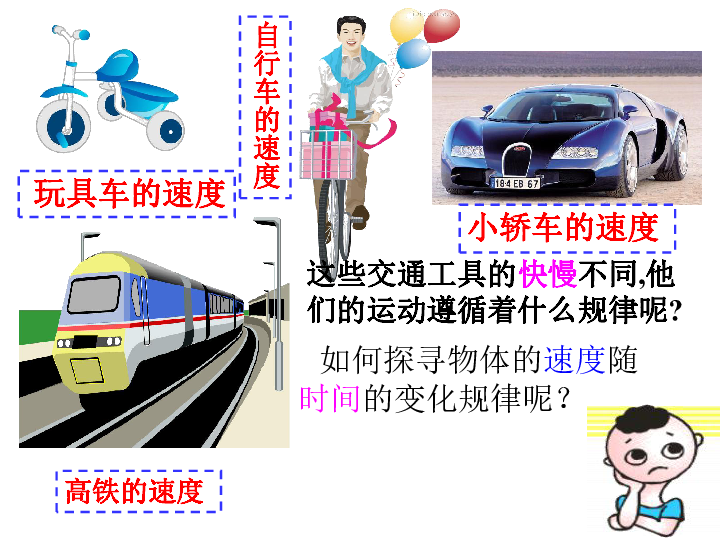
匀速直线运动的速度图象(v-t图象)
t/s
x/m
0
0.02 0.04 0.06 0.08 0.10 0.12
0.02
0.04
0.06
交流与讨论:你能根据上图所描述的匀速直线运动,画出它的速度时间图象吗?
t/s
v/m·s-1
0
0.02 0.04 0.06 0.08 0.10 0.12
0.5
第二章 匀变速直线运动的研究
第一节
实验:探究小车速度随时间变化的规律
玩具车的速度
小轿车的速度
自行车的速度
高铁的速度
如何探寻物体的速度随时间的变化规律呢?
这些交通工具的快慢不同,他们的运动遵循着什么规律呢?
实验室如何探究小车的运动速度与时间的关系?
自主学习:
阅读课本P31,“进行实验”部分,思考下列问题:
(1)如何设计实验方案?
(2)要想进行实验,需要哪些实验器材?
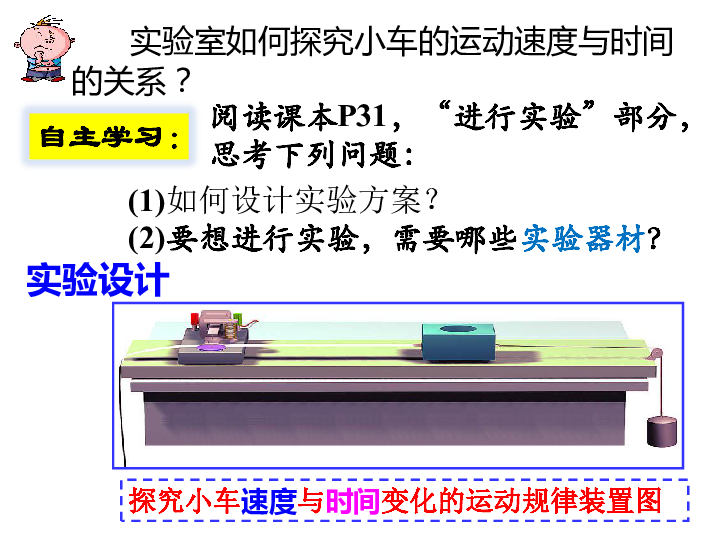
探究小车速度与时间变化的运动规律装置图
实验设计
实验用具
⑤附有滑轮的长木板
④小车
⑦带小钩的细线
⑥25g的钩码3个,也可以用50g的钩码
①打点计时器
③纸带
⑧刻度尺
②学生电源、导线。
(4)换上新纸带,重复操作三次。
实验步骤
(1)把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,把打点计时器固定在长木板上没有滑轮的一端,连接好电路。
(2)把一条细绳栓在小车上,使细绳跨过滑轮,下边挂上合适的砝码,把纸带穿过限位孔。
(3)小车停在靠近打点计时器处,启动电源,后释放小车,让小车拖动纸带运动,打完一条纸带后立即关闭电源。
一、进行实验
(1)固定打点计时器时应让限位孔处在长木
板的中央位置。
(2)调节滑轮高度时,细绳应与木板平行。
(3)应考虑复写纸与纸带的位置关系。
(4)钩码数量不能过多,也不能过少。
(5)小车应由紧靠打点计时器处开始释放,在
撞击长木板末端前应让小车停止运动,防止
小车从板上掉下来。
(6)先接通电源,后让纸带运动。
(7)打点结束后立即关闭电源。
注意事项
若纸带上点与点之间的距离较小,每五个计时点取一个计数点 ,依次标号为0,1,2,3,4,5 (间隔是0.1s)。
0.10s
0.10s
过于密集/不清晰的点
问题1:怎样分析和选取纸带上的点?
舍掉开头过于密集的点,从清楚的点开始
二、数据处理
(2)用求平均速度的方法来求[选择包括该点在内的一段位移Δx(该点最好处在中间时刻位置),找出对应的时间Δt,用Δx/Δt作为该点的瞬时速度];
△x1
△x2
△x3
△x4
△x5
问题2:如何计算出所取点的瞬时速度?
(1)测量各个计数点之间的距离应注意估读、单位。
△x 4 -△x 2
v3 = v24 = ——— = —————
2△t
△x 24
2△t
△t为多少?
例:求3这个计数点的速度:
△x1
△x2
△x3
△x4
△x5
小车的瞬时速度随时间增大而增大。
思考:小车的具体运动规律是什么?
- -
0.201
0.280
0.432
0.355
0.512
同理,可求出另外两条纸带的情况
数据处理列表法
①根据所得数据,选择合适的标度建立直角坐标系(图象尽量分布在坐标系平面的大部分面积)
②根据所得数据描出各点的位置(描点法),观察和思考各点的分布规律
数据处理图像法:
速度时间图像(v-t图像):
用纵坐标表示速度,横坐标表示时间,建立直角坐标系,画出的速度随时间变化而变化的图像。
0.1
0.2
0.3
0.4
0.5
0.6
t/s
o
0.10
0.20
0.30
0.40
v/(m/s)
×
×
×
×
×
与纵轴的交点是什么意思?
如何求加速度?
△t=0.35s
△v=?
0.27m/s
0.50
思考:从速度图像中我们又可以获得哪些信息呢?
0.47
3/10/11/
1)匀变速直线运动的v-t图象是一条倾斜的直线
2)直线与纵坐标的交点即为物体的初速度;
4)直线的斜率表示物体的加速度:
匀变速直线运动的速度时间图象:
3)可以确定物体各个时刻所对应的速度
几何图的面积=长×宽
匀速直线运动物体的位移s=v t 或x=v t
联想
5)在v-t图中,图线与坐标轴之间覆盖的面积可表示位移大小和方向。
梯形的面积
v-t图中物体的位移
联想
思考与讨论:如图所示,Ⅰ、Ⅱ是做什么运动?有何区别?
30
20
10
2
4
v/m.s-1
t/s
Ⅱ
Ⅰ
-10
两图像的交点表示速度相等
思考与探究:
一辆汽车在匀加速行驶中以速度为v0,经过某一路标时的速度图线如图所示,t0秒末速度为vto求此后t0秒内汽车的平均速度是多少?中间时刻的速度呢?
v/m.s-1
t/s
0
v0
vt0
t0
t0/2
vt0/2
t1
t2
t3
t4
v1
v2
v3
v4
0
v
t
思考与讨论:
1、如图是一个物体运动的v-t图象,它的速度怎样变化?
2、在相等的时间间隔内,速度的变化量相等吗?
3、物体做什么直线运动?
加速度逐渐减小的加速运动
例1、如图所示,一物体做直线运动的v—t图象,问:
(1)图中OA、AB、BC、CD、DE各表示怎样的运动?
(2)哪个过程的加速度最大?第4s内的位移多大?
(3)5s内物体的位移和路程各是多少?
v/m
t/s
10
20
30
1 2 3 4 5 6 7
0
A
B
C
D
-10
x/m
t/s
10
20
30
1 2 3 4 5
0
A
B
C
D
例2、某物体的位移-时间图象如下图所示,试在右图画出它的速度时间图象
v/m·s-1
t/s
10
20
1 2 3 4 5
0
A
B
C
D
-10
-20
-30
例3、比较下面两个直线运动
x/m
t/s
4
8
10
0
-10
t/s
4
8
10
0
-10
v/m·s-1
甲
乙
(1)甲、乙两物体何时距离出发点最远?
(2)甲、乙两物体何时返回出发点?
[例2](2018·天水高一检测)在“探究小车速度随时间变化的规律”的实验中,如下图所示为记录小车运动情况的一条纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间的时间间隔T=0.1 s。
《创新设计》P20
(1)计算D、C、B各点的瞬时速度,vD=____ m/s,vC=______ m/s,vB=______ m/s。
答案(1)3.90 2.64 1.38
12
(2)在如图4所示坐标系中作出小车的v-t图象,并根据图象求出a=________。
12.6 m/s2
[针对训练3](多选)若某物体做直线运动的v-t
图象如图所示,则下列说法中正确的是( )
A.t=3 s时物体运动的速度方向发生改变
B.t=3 s时物体运动的加速度方向发生改变
C.t=3 s时物体离出发点最远
D.t=3 s时物体的加速度为零
《创新设计》P16
AC
(多选)甲、乙两个物体在同一直线上运动,它们的v-t图象如图所示,则在t1时刻( )
A.甲、乙运动的速度大小相等,方向相反 B.甲、乙运动的速度大小相等,方向相同 C.甲、乙运动的加速度大小不等,方向相同 D.甲、乙运动的加速度大小不等,方向相反
《创新设计》P16(课时达标训练T5)
BD
直线运动的二类图像对比
图像 x ?t图像 v ?t图像
图像实例
图线含义 图线①表示质点做匀速直线运动(斜率表示速度v) 图线①表示质点做匀加速直线运动(斜率表示加速度a)
图线②表示质点静止 图线②表示质点做匀速直线运动
图线③表示质点向负方向做匀速直线运动 图线③表示质点做匀减速直线运动
交点④表示此时三个质点相遇 交点④表示此时三个质点有相同的速度
点⑤表示t1时刻质点位移为x1(图中阴影部分的面积没有意义) 点⑤表示t1时刻质点速度为v1(图中阴影部分面积表示质点在0~t1时间内的位移)
可以。剪下的纸条长度表示0.1 s时间内位移大小,可近似认为速度 ??? . v∝Δx,纸条长度可认为表示速度
问题与练习P33 T3
作业完成《创新设计》P20~21
并订正。
匀速直线运动的速度图象(v-t图象)
t/s
x/m
0
0.02 0.04 0.06 0.08 0.10 0.12
0.02
0.04
0.06
交流与讨论:你能根据上图所描述的匀速直线运动,画出它的速度时间图象吗?
t/s
v/m·s-1
0
0.02 0.04 0.06 0.08 0.10 0.12
0.5
第二章 匀变速直线运动的研究
第一节
实验:探究小车速度随时间变化的规律
玩具车的速度
小轿车的速度
自行车的速度
高铁的速度
如何探寻物体的速度随时间的变化规律呢?
这些交通工具的快慢不同,他们的运动遵循着什么规律呢?
实验室如何探究小车的运动速度与时间的关系?
自主学习:
阅读课本P31,“进行实验”部分,思考下列问题:
(1)如何设计实验方案?
(2)要想进行实验,需要哪些实验器材?
探究小车速度与时间变化的运动规律装置图
实验设计
实验用具
⑤附有滑轮的长木板
④小车
⑦带小钩的细线
⑥25g的钩码3个,也可以用50g的钩码
①打点计时器
③纸带
⑧刻度尺
②学生电源、导线。
(4)换上新纸带,重复操作三次。
实验步骤
(1)把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,把打点计时器固定在长木板上没有滑轮的一端,连接好电路。
(2)把一条细绳栓在小车上,使细绳跨过滑轮,下边挂上合适的砝码,把纸带穿过限位孔。
(3)小车停在靠近打点计时器处,启动电源,后释放小车,让小车拖动纸带运动,打完一条纸带后立即关闭电源。
一、进行实验
(1)固定打点计时器时应让限位孔处在长木
板的中央位置。
(2)调节滑轮高度时,细绳应与木板平行。
(3)应考虑复写纸与纸带的位置关系。
(4)钩码数量不能过多,也不能过少。
(5)小车应由紧靠打点计时器处开始释放,在
撞击长木板末端前应让小车停止运动,防止
小车从板上掉下来。
(6)先接通电源,后让纸带运动。
(7)打点结束后立即关闭电源。
注意事项
若纸带上点与点之间的距离较小,每五个计时点取一个计数点 ,依次标号为0,1,2,3,4,5 (间隔是0.1s)。
0.10s
0.10s
过于密集/不清晰的点
问题1:怎样分析和选取纸带上的点?
舍掉开头过于密集的点,从清楚的点开始
二、数据处理
(2)用求平均速度的方法来求[选择包括该点在内的一段位移Δx(该点最好处在中间时刻位置),找出对应的时间Δt,用Δx/Δt作为该点的瞬时速度];
△x1
△x2
△x3
△x4
△x5
问题2:如何计算出所取点的瞬时速度?
(1)测量各个计数点之间的距离应注意估读、单位。
△x 4 -△x 2
v3 = v24 = ——— = —————
2△t
△x 24
2△t
△t为多少?
例:求3这个计数点的速度:
△x1
△x2
△x3
△x4
△x5
小车的瞬时速度随时间增大而增大。
思考:小车的具体运动规律是什么?
- -
0.201
0.280
0.432
0.355
0.512
同理,可求出另外两条纸带的情况
数据处理列表法
①根据所得数据,选择合适的标度建立直角坐标系(图象尽量分布在坐标系平面的大部分面积)
②根据所得数据描出各点的位置(描点法),观察和思考各点的分布规律
数据处理图像法:
速度时间图像(v-t图像):
用纵坐标表示速度,横坐标表示时间,建立直角坐标系,画出的速度随时间变化而变化的图像。
0.1
0.2
0.3
0.4
0.5
0.6
t/s
o
0.10
0.20
0.30
0.40
v/(m/s)
×
×
×
×
×
与纵轴的交点是什么意思?
如何求加速度?
△t=0.35s
△v=?
0.27m/s
0.50
思考:从速度图像中我们又可以获得哪些信息呢?
0.47
3/10/11/
1)匀变速直线运动的v-t图象是一条倾斜的直线
2)直线与纵坐标的交点即为物体的初速度;
4)直线的斜率表示物体的加速度:
匀变速直线运动的速度时间图象:
3)可以确定物体各个时刻所对应的速度
几何图的面积=长×宽
匀速直线运动物体的位移s=v t 或x=v t
联想
5)在v-t图中,图线与坐标轴之间覆盖的面积可表示位移大小和方向。
梯形的面积
v-t图中物体的位移
联想
思考与讨论:如图所示,Ⅰ、Ⅱ是做什么运动?有何区别?
30
20
10
2
4
v/m.s-1
t/s
Ⅱ
Ⅰ
-10
两图像的交点表示速度相等
思考与探究:
一辆汽车在匀加速行驶中以速度为v0,经过某一路标时的速度图线如图所示,t0秒末速度为vto求此后t0秒内汽车的平均速度是多少?中间时刻的速度呢?
v/m.s-1
t/s
0
v0
vt0
t0
t0/2
vt0/2
t1
t2
t3
t4
v1
v2
v3
v4
0
v
t
思考与讨论:
1、如图是一个物体运动的v-t图象,它的速度怎样变化?
2、在相等的时间间隔内,速度的变化量相等吗?
3、物体做什么直线运动?
加速度逐渐减小的加速运动
例1、如图所示,一物体做直线运动的v—t图象,问:
(1)图中OA、AB、BC、CD、DE各表示怎样的运动?
(2)哪个过程的加速度最大?第4s内的位移多大?
(3)5s内物体的位移和路程各是多少?
v/m
t/s
10
20
30
1 2 3 4 5 6 7
0
A
B
C
D
-10
x/m
t/s
10
20
30
1 2 3 4 5
0
A
B
C
D
例2、某物体的位移-时间图象如下图所示,试在右图画出它的速度时间图象
v/m·s-1
t/s
10
20
1 2 3 4 5
0
A
B
C
D
-10
-20
-30
例3、比较下面两个直线运动
x/m
t/s
4
8
10
0
-10
t/s
4
8
10
0
-10
v/m·s-1
甲
乙
(1)甲、乙两物体何时距离出发点最远?
(2)甲、乙两物体何时返回出发点?
[例2](2018·天水高一检测)在“探究小车速度随时间变化的规律”的实验中,如下图所示为记录小车运动情况的一条纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间的时间间隔T=0.1 s。
《创新设计》P20
(1)计算D、C、B各点的瞬时速度,vD=____ m/s,vC=______ m/s,vB=______ m/s。
答案(1)3.90 2.64 1.38
12
(2)在如图4所示坐标系中作出小车的v-t图象,并根据图象求出a=________。
12.6 m/s2
[针对训练3](多选)若某物体做直线运动的v-t
图象如图所示,则下列说法中正确的是( )
A.t=3 s时物体运动的速度方向发生改变
B.t=3 s时物体运动的加速度方向发生改变
C.t=3 s时物体离出发点最远
D.t=3 s时物体的加速度为零
《创新设计》P16
AC
(多选)甲、乙两个物体在同一直线上运动,它们的v-t图象如图所示,则在t1时刻( )
A.甲、乙运动的速度大小相等,方向相反 B.甲、乙运动的速度大小相等,方向相同 C.甲、乙运动的加速度大小不等,方向相同 D.甲、乙运动的加速度大小不等,方向相反
《创新设计》P16(课时达标训练T5)
BD
直线运动的二类图像对比
图像 x ?t图像 v ?t图像
图像实例
图线含义 图线①表示质点做匀速直线运动(斜率表示速度v) 图线①表示质点做匀加速直线运动(斜率表示加速度a)
图线②表示质点静止 图线②表示质点做匀速直线运动
图线③表示质点向负方向做匀速直线运动 图线③表示质点做匀减速直线运动
交点④表示此时三个质点相遇 交点④表示此时三个质点有相同的速度
点⑤表示t1时刻质点位移为x1(图中阴影部分的面积没有意义) 点⑤表示t1时刻质点速度为v1(图中阴影部分面积表示质点在0~t1时间内的位移)
可以。剪下的纸条长度表示0.1 s时间内位移大小,可近似认为速度 ??? . v∝Δx,纸条长度可认为表示速度
问题与练习P33 T3
作业完成《创新设计》P20~21
并订正。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
