24.3 圆周角(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.3 圆周角(基础达标+巩固提升+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
沪科版数学九年级下册同步课时训练
第24章
圆
24.3 圆周角
要点测评
基础达标
要点1 圆周角和圆周角定理
1.
如图,在☉O中,
QUOTE
=
QUOTE
,∠AOB=40°,则∠ADC的度数是(
)
A.
40°
B.
30°
C.
20°
D.
15°
2.
如图,☉O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为(
)
A.
2
QUOTE
B.
4
C.
4
QUOTE
D.
8
要点2 利用圆周角定理及其推论计算
3.
如图,AB为☉O的直径,C,D为☉O上的点,
QUOTE
=
QUOTE
,若∠CAB=40°,则∠CAD=
.
4.
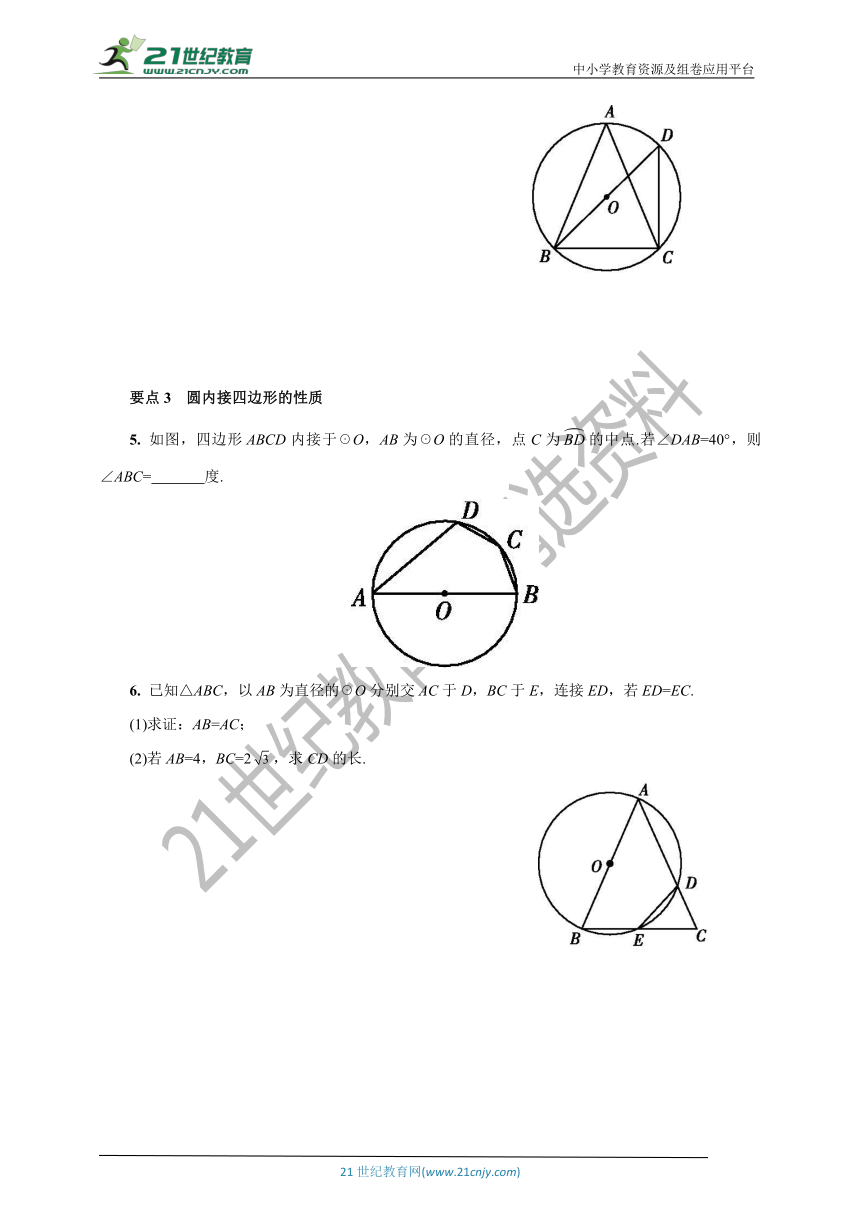
如图,☉O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
要点3 圆内接四边形的性质
5.
如图,四边形ABCD内接于☉O,AB为☉O的直径,点C为的中点.若∠DAB=40°,则∠ABC=
度.
6.
已知△ABC,以AB为直径的☉O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2
QUOTE
,求CD的长.
课后集训
巩固提升
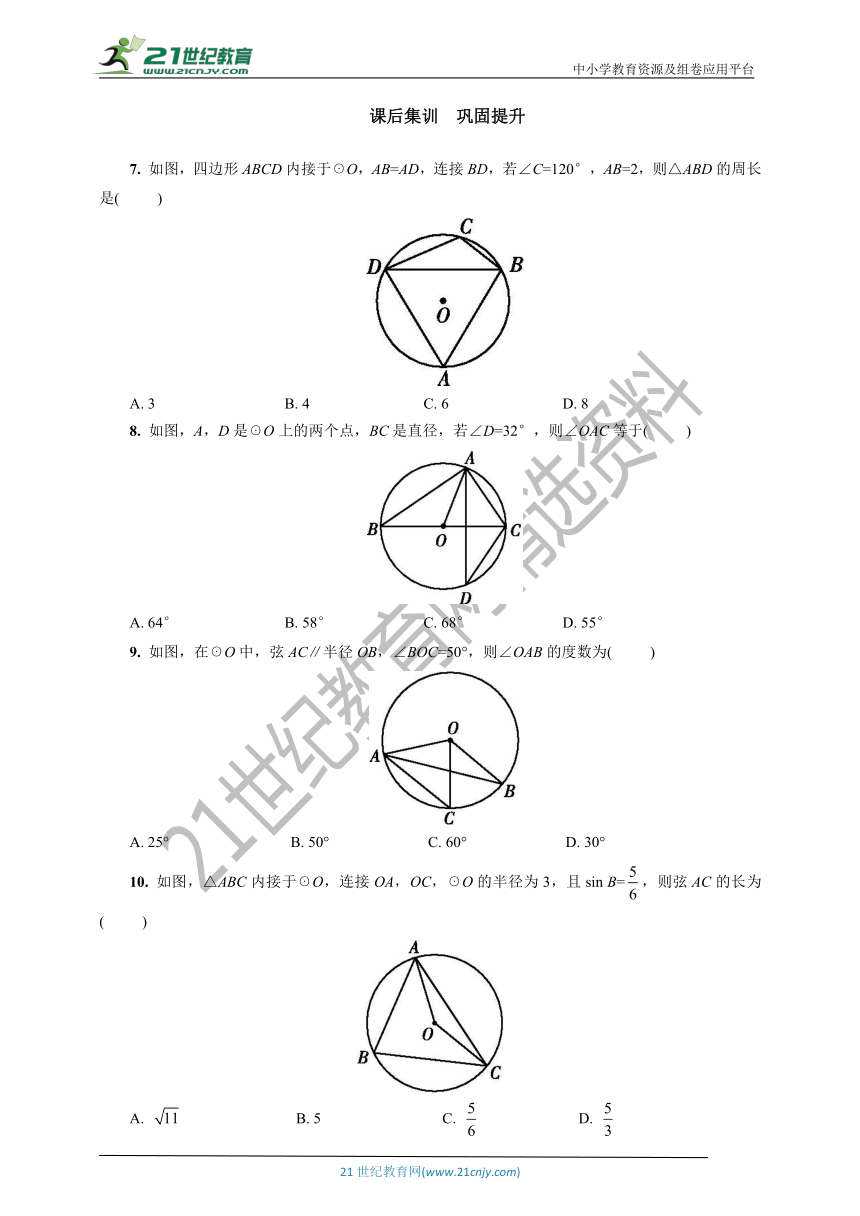
7.
如图,四边形ABCD内接于☉O,AB=AD,连接BD,若∠C=120°,AB=2,则△ABD的周长是(
)
A.
3
B.
4
C.
6
D.
8
8.
如图,A,D是☉O上的两个点,BC是直径,若∠D=32°,则∠OAC等于(
)
A.
64°
B.
58°
C.
68°
D.
55°
9.
如图,在☉O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为(
)
A.
25°
B.
50°
C.
60°
D.
30°
10.
如图,△ABC内接于☉O,连接OA,OC,☉O的半径为3,且sin
B=,则弦AC的长为(
)
A.
B.
5
C.
D.
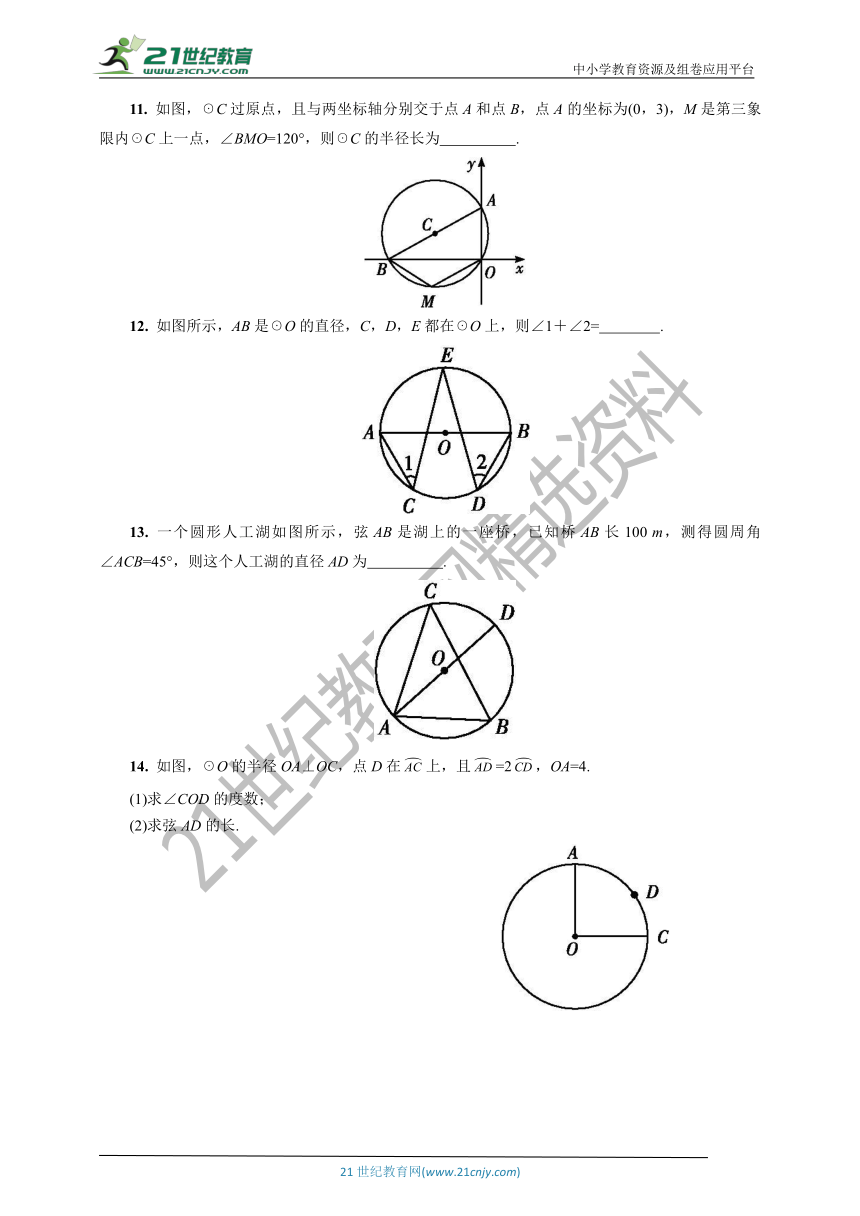
11.
如图,☉C过原点,且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),M是第三象限内☉C上一点,∠BMO=120°,则☉C的半径长为
.
12.
如图所示,AB是☉O的直径,C,D,E都在☉O上,则∠1+∠2=
.
13.
一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100
m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为
.
14.
如图,☉O的半径OA⊥OC,点D在
QUOTE
上,且
QUOTE
=2
QUOTE
,OA=4.
(1)求∠COD的度数;
(2)求弦AD的长.
15.
如图,AC是☉O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
参
考
答
案
1.
C 【解析】连接CO,如图,因为在☉O中,=,所以∠AOC=∠AOB,因为∠AOB=40°,所以∠AOC=40°,所以∠ADC=∠AOC=20°,故选C.
2.
C 【解析】因为∠A=22.5°,所以∠BOC=2∠A=45°,因为☉O的直径AB垂直于弦CD,所以CE=DE,△OCE为等腰直角三角形,所以CE=OC=2,所以CD=2CE=4.故选C.
3.
25° 【解析】如图,连接BC,BD,因为AB是☉O的直径,C,D为☉O上的点,所以∠ACB=90°,因为∠CAB=40°,所以∠CBA=50°,因为=,所以∠CBD=∠DBA=∠CBA=25°,所以∠CAD=∠CBD=25°.
4.
解:在☉O中,因为∠A=45°,所以∠D=45°,因为BD为☉O的直径,所以∠BCD=90°,所以△BCD是等腰直角三角形,所以BC=BD·sin
45°,因为BD=2,所以BC=2×=.
5.
70 【解析】如图,连接BD,因为AB为☉O的直径,所以∠ADB=90°,因为∠DAB=40°,所以∠ABD=90°-∠DAB=50°,∠C=180°-∠DAB=140°,因为点C为的中点,所以CD=CB,所以∠CBD=∠CDB=20°,所以∠ABC=∠ABD+∠CBD=70°.
6.
(1)证明:因为ED=EC,所以∠EDC=∠C,因为四边形ABED为圆O的内接四边形,所以∠B+∠ADE=180°,又因为∠ADE+∠EDC=180°,所以∠EDC=∠B,所以∠B=∠C,所以AB=AC.
(2)解:如图,连接AE,因为AB为直径,所以AE⊥BC,由(1)知AB=AC,所以BE=CE=BC=,因为△CDE∽△CBA,所以=,所以CE·CB=CD·CA,AC=AB=4,所以·2=4CD,所以CD=.
7.
C 【解析】因为四边形ABCD内接于☉O,∠C=120°,所以∠A=180°-120°=60°.因为AB=AD,AB=2,所以△ABD是等边三角形,所以△ABD的周长=2×3=6.故选C.
8.
B 【解析】因为BC是直径,∠D=32°,所以∠B=∠D=32°,∠BAC=90°.因为OA=OB,所以∠BAO=∠B=32°,所以∠OAC=∠BAC-∠BAO=90°-32°=58°.故选B.
9.
A 【解析】因为∠BOC=2∠BAC,∠BOC=50°,所以∠BAC=25°,因为AC∥OB,所以∠BAC=∠B=25°,因为OA=OB,所以∠OAB=∠B=25°,故选A.
10.
B 【解析】如图,延长AO,交☉O于点E,连接CE,所以∠AEC=∠B,因为AE是☉O的直径,所以∠ACE=90°,在直角三角形ACE中,因为sin
B=,所以=,因为AO=3,所以AE=6,所以AC=5,故选B.
11.
3 【解析】因为四边形ABMO是圆内接四边形,∠BMO=120°,所以∠BAO=60°,因为AB是☉C的直径,所以∠AOB=90°,所以∠ABO=90°-∠BAO=90°-60°=30°,因为点A的坐标为(0,3),所以OA=3,所以AB=2OA=6,所以☉C的半径长为=3.
12.
90° 【解析】如图,连接AD,因为AB是☉O的直径,所以∠ADB=90°.又因为∠1=∠ADE,所以∠1+∠2=∠ADE+∠2=∠ADB=90°.
13.
100m 【解析】如图,连接BD,因为AD是直径,所以∠ABD=90°.易知∠D=∠ACB=45°,在Rt△ADB中,sin
∠D=,即=,所以AD=100m.
14.
解:(1)因为OA⊥OC,所以∠AOC=90°,因为=2,所以∠AOD=2∠COD,所以∠COD=∠AOC=30°.
(2)连接OD,AD,如图所示.由(1)知∠AOD=2∠COD=2×30°=60°,因为OA=OD,所以△AOD为等边三角形,所以AD=OA=4.
15.
证明:(1)如图,因为=,所以∠A=∠B.又因为∠1=∠2,所以△ADE∽△BCE.(2)由AD2=AE·AC得=.又因为∠A=∠A,所以△ADE∽△ACD,所以∠AED=∠ADC.又因为AC是☉O的直径,所以∠ADC=90°,所以∠AED=90°,所以AC⊥BD,所以CD=CB.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
沪科版数学九年级下册同步课时训练
第24章
圆
24.3 圆周角
要点测评
基础达标
要点1 圆周角和圆周角定理
1.
如图,在☉O中,
QUOTE
=
QUOTE
,∠AOB=40°,则∠ADC的度数是(
)
A.
40°
B.
30°
C.
20°
D.
15°
2.
如图,☉O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为(
)
A.
2
QUOTE
B.
4
C.
4
QUOTE
D.
8
要点2 利用圆周角定理及其推论计算
3.
如图,AB为☉O的直径,C,D为☉O上的点,
QUOTE
=
QUOTE
,若∠CAB=40°,则∠CAD=
.
4.
如图,☉O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
要点3 圆内接四边形的性质
5.
如图,四边形ABCD内接于☉O,AB为☉O的直径,点C为的中点.若∠DAB=40°,则∠ABC=
度.
6.
已知△ABC,以AB为直径的☉O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2
QUOTE
,求CD的长.
课后集训
巩固提升
7.
如图,四边形ABCD内接于☉O,AB=AD,连接BD,若∠C=120°,AB=2,则△ABD的周长是(
)
A.
3
B.
4
C.
6
D.
8
8.
如图,A,D是☉O上的两个点,BC是直径,若∠D=32°,则∠OAC等于(
)
A.
64°
B.
58°
C.
68°
D.
55°
9.
如图,在☉O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为(
)
A.
25°
B.
50°
C.
60°
D.
30°
10.
如图,△ABC内接于☉O,连接OA,OC,☉O的半径为3,且sin
B=,则弦AC的长为(
)
A.
B.
5
C.
D.
11.
如图,☉C过原点,且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),M是第三象限内☉C上一点,∠BMO=120°,则☉C的半径长为
.
12.
如图所示,AB是☉O的直径,C,D,E都在☉O上,则∠1+∠2=
.
13.
一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100
m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为
.
14.
如图,☉O的半径OA⊥OC,点D在
QUOTE
上,且
QUOTE
=2
QUOTE
,OA=4.
(1)求∠COD的度数;
(2)求弦AD的长.
15.
如图,AC是☉O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
参
考
答
案
1.
C 【解析】连接CO,如图,因为在☉O中,=,所以∠AOC=∠AOB,因为∠AOB=40°,所以∠AOC=40°,所以∠ADC=∠AOC=20°,故选C.
2.
C 【解析】因为∠A=22.5°,所以∠BOC=2∠A=45°,因为☉O的直径AB垂直于弦CD,所以CE=DE,△OCE为等腰直角三角形,所以CE=OC=2,所以CD=2CE=4.故选C.
3.
25° 【解析】如图,连接BC,BD,因为AB是☉O的直径,C,D为☉O上的点,所以∠ACB=90°,因为∠CAB=40°,所以∠CBA=50°,因为=,所以∠CBD=∠DBA=∠CBA=25°,所以∠CAD=∠CBD=25°.
4.
解:在☉O中,因为∠A=45°,所以∠D=45°,因为BD为☉O的直径,所以∠BCD=90°,所以△BCD是等腰直角三角形,所以BC=BD·sin
45°,因为BD=2,所以BC=2×=.
5.
70 【解析】如图,连接BD,因为AB为☉O的直径,所以∠ADB=90°,因为∠DAB=40°,所以∠ABD=90°-∠DAB=50°,∠C=180°-∠DAB=140°,因为点C为的中点,所以CD=CB,所以∠CBD=∠CDB=20°,所以∠ABC=∠ABD+∠CBD=70°.
6.
(1)证明:因为ED=EC,所以∠EDC=∠C,因为四边形ABED为圆O的内接四边形,所以∠B+∠ADE=180°,又因为∠ADE+∠EDC=180°,所以∠EDC=∠B,所以∠B=∠C,所以AB=AC.
(2)解:如图,连接AE,因为AB为直径,所以AE⊥BC,由(1)知AB=AC,所以BE=CE=BC=,因为△CDE∽△CBA,所以=,所以CE·CB=CD·CA,AC=AB=4,所以·2=4CD,所以CD=.
7.
C 【解析】因为四边形ABCD内接于☉O,∠C=120°,所以∠A=180°-120°=60°.因为AB=AD,AB=2,所以△ABD是等边三角形,所以△ABD的周长=2×3=6.故选C.
8.
B 【解析】因为BC是直径,∠D=32°,所以∠B=∠D=32°,∠BAC=90°.因为OA=OB,所以∠BAO=∠B=32°,所以∠OAC=∠BAC-∠BAO=90°-32°=58°.故选B.
9.
A 【解析】因为∠BOC=2∠BAC,∠BOC=50°,所以∠BAC=25°,因为AC∥OB,所以∠BAC=∠B=25°,因为OA=OB,所以∠OAB=∠B=25°,故选A.
10.
B 【解析】如图,延长AO,交☉O于点E,连接CE,所以∠AEC=∠B,因为AE是☉O的直径,所以∠ACE=90°,在直角三角形ACE中,因为sin
B=,所以=,因为AO=3,所以AE=6,所以AC=5,故选B.
11.
3 【解析】因为四边形ABMO是圆内接四边形,∠BMO=120°,所以∠BAO=60°,因为AB是☉C的直径,所以∠AOB=90°,所以∠ABO=90°-∠BAO=90°-60°=30°,因为点A的坐标为(0,3),所以OA=3,所以AB=2OA=6,所以☉C的半径长为=3.
12.
90° 【解析】如图,连接AD,因为AB是☉O的直径,所以∠ADB=90°.又因为∠1=∠ADE,所以∠1+∠2=∠ADE+∠2=∠ADB=90°.
13.
100m 【解析】如图,连接BD,因为AD是直径,所以∠ABD=90°.易知∠D=∠ACB=45°,在Rt△ADB中,sin
∠D=,即=,所以AD=100m.
14.
解:(1)因为OA⊥OC,所以∠AOC=90°,因为=2,所以∠AOD=2∠COD,所以∠COD=∠AOC=30°.
(2)连接OD,AD,如图所示.由(1)知∠AOD=2∠COD=2×30°=60°,因为OA=OD,所以△AOD为等边三角形,所以AD=OA=4.
15.
证明:(1)如图,因为=,所以∠A=∠B.又因为∠1=∠2,所以△ADE∽△BCE.(2)由AD2=AE·AC得=.又因为∠A=∠A,所以△ADE∽△ACD,所以∠AED=∠ADC.又因为AC是☉O的直径,所以∠ADC=90°,所以∠AED=90°,所以AC⊥BD,所以CD=CB.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
