六年级上册数学试题-《圆、位置与方向、数与形》分层训练 人教版(含答案)
文档属性
| 名称 | 六年级上册数学试题-《圆、位置与方向、数与形》分层训练 人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-01 00:00:00 | ||
图片预览

文档简介
《圆、位置与方向、数与形》分层训练
易错通关
1.填空题。
(1)要画一个周长是15.7dm的圆,圆规两脚间的距离是(
)dm,画出的圆的面积(
)dm 。
(2)A圆的直径是B圆的,A圆的周长与B圆周长的比是(
),A圆的面积是B圆的。
(3)一对相互咬合的齿轮,大齿轮的直径是6cm,小齿轮的直径是3cm,大齿轮转动4周时,小齿轮转动(
)周。
(4)一个圆的周长是12.56cm,如果把它分成两个相等的半圆,那么其中一个半圆的周长是(
)cm,面积是(
)cm 。
(5)把一个直径是12厘米的圆沿半径剪成若干等份,拼成一个近似的长方形,拼成的长方形的周长是(
)厘米,面积是(
)平方厘米。
(6)乐乐做了一个圆环形花环,如果这个花环的内圆周长是12.56厘米,环宽1厘米,那么外圆的半径是(
)厘米,周长是(
)厘米,这个环形的面积是(
)
平方厘米。
(7)小明在笑笑的东偏南30°方向15m处,那么笑笑在小明的(
)偏(
)(
)°方向(
)m处。
(8)观察下图中每一个大三角形中涂色三角形的排列规律,则第6个图形中涂色三角形有(
)个。
2.选择题。
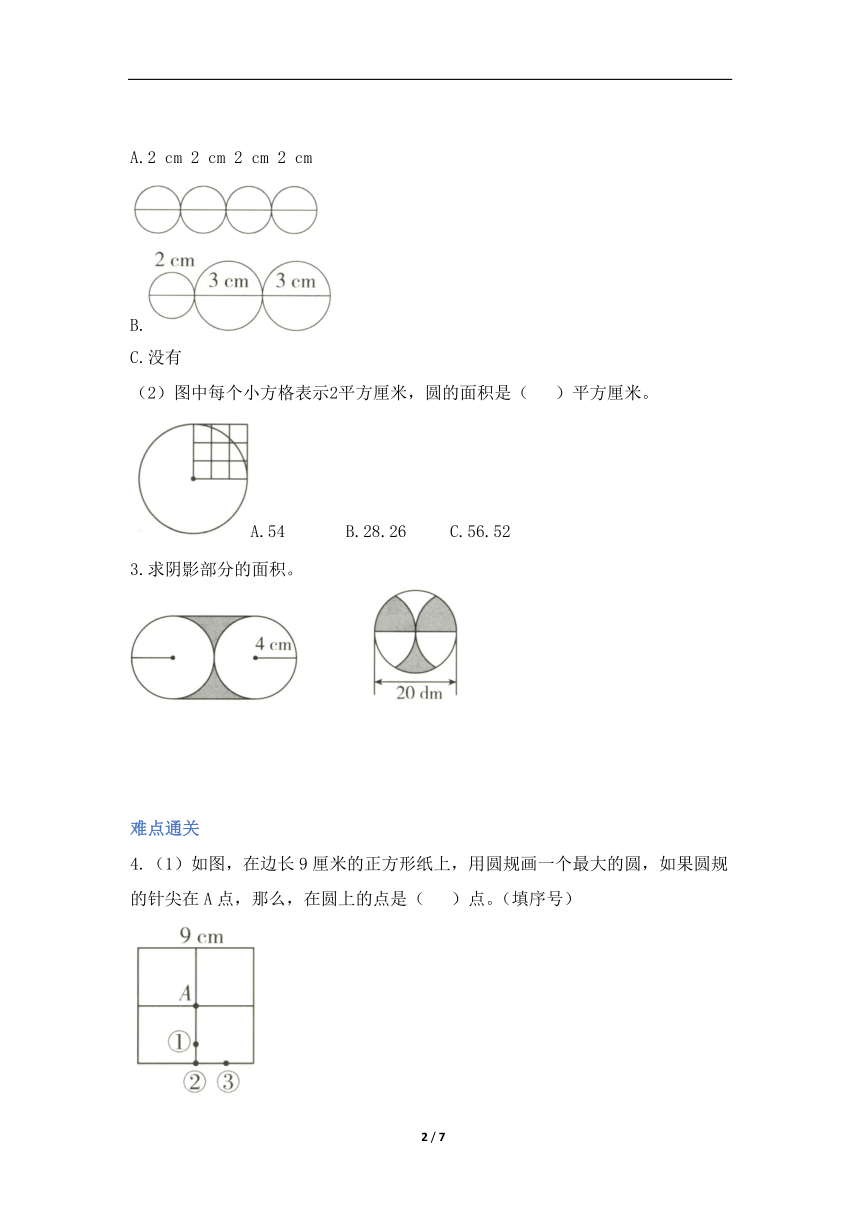
(1)下列图形的周长之和不能用3.14×8计算的是(
)。
A.2
cm
2
cm
2
cm
2
cm
B.
C.没有
(2)图中每个小方格表示2平方厘米,圆的面积是(
)平方厘米。
A.54
B.28.26
C.56.52
3.求阴影部分的面积。
难点通关
4.(1)如图,在边长9厘米的正方形纸上,用圆规画一个最大的圆,如果圆规的针尖在A点,那么,在圆上的点是(
)点。(填序号)
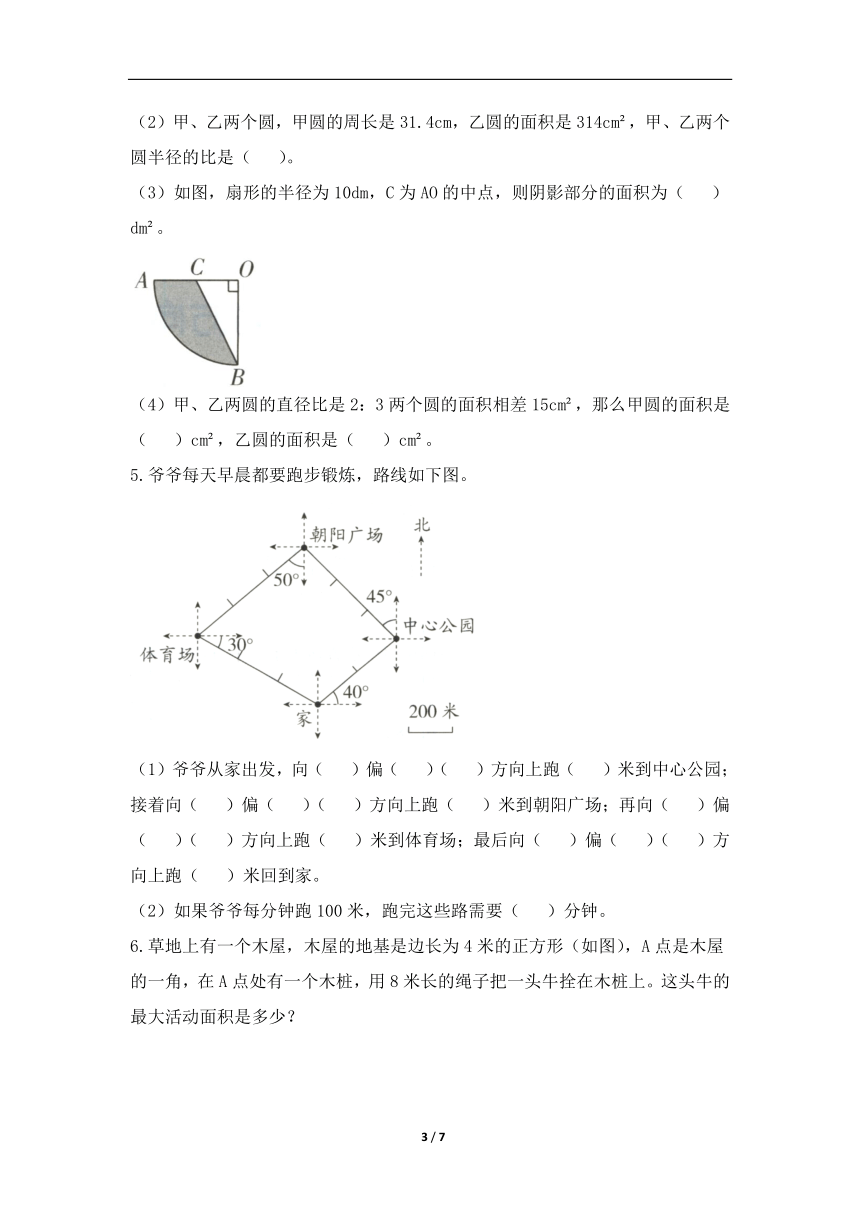
(2)甲、乙两个圆,甲圆的周长是31.4cm,乙圆的面积是314cm ,甲、乙两个圆半径的比是(
)。
(3)如图,扇形的半径为10dm,C为AO的中点,则阴影部分的面积为(
)dm 。
(4)甲、乙两圆的直径比是2:3两个圆的面积相差15cm ,那么甲圆的面积是(
)cm ,乙圆的面积是(
)cm 。
5.爷爷每天早晨都要跑步锻炼,路线如下图。
(1)爷爷从家出发,向(
)偏(
)(
)方向上跑(
)米到中心公园;接着向(
)偏(
)(
)方向上跑(
)米到朝阳广场;再向(
)偏(
)(
)方向上跑(
)米到体育场;最后向(
)偏(
)(
)方向上跑(
)米回到家。
(2)如果爷爷每分钟跑100米,跑完这些路需要(
)分钟。
6.草地上有一个木屋,木屋的地基是边长为4米的正方形(如图),A点是木屋的一角,在A点处有一个木桩,用8米长的绳子把一头牛拴在木桩上。这头牛的最大活动面积是多少?
7.如图,将三根半径为15cm的圆木用铁丝紧紧捆在一起,至少需要铁丝多少厘米?(接头处为12cm)
8.如图所示,边长为12厘米的正方形与直径为16厘米的圆有部分重叠(圆心是正方形的一个顶点),用S1,S2分别表示两块空白部分的面积,求S1-S2的值。
9.如图所示,地面上平躺着一个底面半径为0.5米的圆柱形油桶。如果要将这个油桶滚到墙边,需要滚动几圈?
10.如图中阴影部分的面积是1.72平方厘米求正方形的面积和圆的面积。
参考答案:
1.(1)2.5
19.625
(2)2:3
(3)8
(4)10.28
6.28
(5)49.68
113.04
提示:拼成的长方形的周长是圆的周长+2条半径。
(6)3
18.84
15.7
(7)西
北
30
15(或北
西
60
15)(8)729
2.(1)C
提示:A中圆的周长和是4×3.14×2=8×3.14;
B中圆的周长和是2×3.14+3×3.14+3×3.14=8×3.14。
(2)C
提示:r =18。
3.8×8-3.14×4 =13.76(cm )3.14×(20÷2) +2=157(dm )
4.(1)画图略
②
提示:图中以A点为圆心,半径是4.5厘米,而②表示的点离A点的距离是4.5厘米,因此②表示的点在圆上。
(2)1:2
提示:甲圆的周长是31.4cm,则甲圆的半径是31.4÷3.14÷2=5(cm)。乙圆的面积是314cm ,314÷3.14=100,而100=10×10,因此乙圆的半径是10cm。甲、乙两个圆半径的比是5:10=1:2。
(3)53.5
提示:阴影部分的面积是四分之一圆的面积减去三角形OCB的面积。
(4)12
27
提示:直径比是2:3,则面积比是4:9,转化成差倍问题计算。
5.(1)东
北
40°
400
北
西
45°
600
南
西
50°600东
南
30°
600(部分答案不唯一)
(2)22
6.3.14×8 ÷4×3+3.14×4 ÷2=175.84(平方米)
7.15×2×3+3.14×15×2+12=196.2(厘米)
8.S1-S2=(S1+S阴)-(S2+S阴)=S圆-S正方形,即3.14×(16÷2) -12 =56.96(平方厘米)
9.2×3.14×0.5=3.14(米)
16.2-0.5=15.7(米)
15.7÷3.14=5(圈)
提示:油桶滚动一圈的距离就是它的底面周长,已知油桶的底面半径,于是就可以根据C=2πr,求出油桶滚动一圈的距离是2×3.14×0.5=3.14(米)。那么这个油桶到底要滚动多少米呢?教大家一个简便的方法:油桶上的一个点移动的距离就是油桶滚动的距离。我们可以来看圆心,它移动的距离应该是16.2-0.5=15.7(米)(如图),所以要将这个油桶滚到墙边滚动的距离是15.7米。
则如果要将这个油桶滚到墙边,需要滚动15.7÷3.14=5(圈)。
10.r =1.72÷(4-3.14)=2正方形的面积:2×4=8(平方厘米)
圆的面积:3.14×2=6.28(平方厘米)
提示:外方内圆时,根据S阴=0.86r ,可先求出r 是多少。
7
/
7
易错通关
1.填空题。
(1)要画一个周长是15.7dm的圆,圆规两脚间的距离是(
)dm,画出的圆的面积(
)dm 。
(2)A圆的直径是B圆的,A圆的周长与B圆周长的比是(
),A圆的面积是B圆的。
(3)一对相互咬合的齿轮,大齿轮的直径是6cm,小齿轮的直径是3cm,大齿轮转动4周时,小齿轮转动(
)周。
(4)一个圆的周长是12.56cm,如果把它分成两个相等的半圆,那么其中一个半圆的周长是(
)cm,面积是(
)cm 。
(5)把一个直径是12厘米的圆沿半径剪成若干等份,拼成一个近似的长方形,拼成的长方形的周长是(
)厘米,面积是(
)平方厘米。
(6)乐乐做了一个圆环形花环,如果这个花环的内圆周长是12.56厘米,环宽1厘米,那么外圆的半径是(
)厘米,周长是(
)厘米,这个环形的面积是(
)
平方厘米。
(7)小明在笑笑的东偏南30°方向15m处,那么笑笑在小明的(
)偏(
)(
)°方向(
)m处。
(8)观察下图中每一个大三角形中涂色三角形的排列规律,则第6个图形中涂色三角形有(
)个。
2.选择题。
(1)下列图形的周长之和不能用3.14×8计算的是(
)。
A.2
cm
2
cm
2
cm
2
cm
B.
C.没有
(2)图中每个小方格表示2平方厘米,圆的面积是(
)平方厘米。
A.54
B.28.26
C.56.52
3.求阴影部分的面积。
难点通关
4.(1)如图,在边长9厘米的正方形纸上,用圆规画一个最大的圆,如果圆规的针尖在A点,那么,在圆上的点是(
)点。(填序号)
(2)甲、乙两个圆,甲圆的周长是31.4cm,乙圆的面积是314cm ,甲、乙两个圆半径的比是(
)。
(3)如图,扇形的半径为10dm,C为AO的中点,则阴影部分的面积为(
)dm 。
(4)甲、乙两圆的直径比是2:3两个圆的面积相差15cm ,那么甲圆的面积是(
)cm ,乙圆的面积是(
)cm 。
5.爷爷每天早晨都要跑步锻炼,路线如下图。
(1)爷爷从家出发,向(
)偏(
)(
)方向上跑(
)米到中心公园;接着向(
)偏(
)(
)方向上跑(
)米到朝阳广场;再向(
)偏(
)(
)方向上跑(
)米到体育场;最后向(
)偏(
)(
)方向上跑(
)米回到家。
(2)如果爷爷每分钟跑100米,跑完这些路需要(
)分钟。
6.草地上有一个木屋,木屋的地基是边长为4米的正方形(如图),A点是木屋的一角,在A点处有一个木桩,用8米长的绳子把一头牛拴在木桩上。这头牛的最大活动面积是多少?
7.如图,将三根半径为15cm的圆木用铁丝紧紧捆在一起,至少需要铁丝多少厘米?(接头处为12cm)
8.如图所示,边长为12厘米的正方形与直径为16厘米的圆有部分重叠(圆心是正方形的一个顶点),用S1,S2分别表示两块空白部分的面积,求S1-S2的值。
9.如图所示,地面上平躺着一个底面半径为0.5米的圆柱形油桶。如果要将这个油桶滚到墙边,需要滚动几圈?
10.如图中阴影部分的面积是1.72平方厘米求正方形的面积和圆的面积。
参考答案:
1.(1)2.5
19.625
(2)2:3
(3)8
(4)10.28
6.28
(5)49.68
113.04
提示:拼成的长方形的周长是圆的周长+2条半径。
(6)3
18.84
15.7
(7)西
北
30
15(或北
西
60
15)(8)729
2.(1)C
提示:A中圆的周长和是4×3.14×2=8×3.14;
B中圆的周长和是2×3.14+3×3.14+3×3.14=8×3.14。
(2)C
提示:r =18。
3.8×8-3.14×4 =13.76(cm )3.14×(20÷2) +2=157(dm )
4.(1)画图略
②
提示:图中以A点为圆心,半径是4.5厘米,而②表示的点离A点的距离是4.5厘米,因此②表示的点在圆上。
(2)1:2
提示:甲圆的周长是31.4cm,则甲圆的半径是31.4÷3.14÷2=5(cm)。乙圆的面积是314cm ,314÷3.14=100,而100=10×10,因此乙圆的半径是10cm。甲、乙两个圆半径的比是5:10=1:2。
(3)53.5
提示:阴影部分的面积是四分之一圆的面积减去三角形OCB的面积。
(4)12
27
提示:直径比是2:3,则面积比是4:9,转化成差倍问题计算。
5.(1)东
北
40°
400
北
西
45°
600
南
西
50°600东
南
30°
600(部分答案不唯一)
(2)22
6.3.14×8 ÷4×3+3.14×4 ÷2=175.84(平方米)
7.15×2×3+3.14×15×2+12=196.2(厘米)
8.S1-S2=(S1+S阴)-(S2+S阴)=S圆-S正方形,即3.14×(16÷2) -12 =56.96(平方厘米)
9.2×3.14×0.5=3.14(米)
16.2-0.5=15.7(米)
15.7÷3.14=5(圈)
提示:油桶滚动一圈的距离就是它的底面周长,已知油桶的底面半径,于是就可以根据C=2πr,求出油桶滚动一圈的距离是2×3.14×0.5=3.14(米)。那么这个油桶到底要滚动多少米呢?教大家一个简便的方法:油桶上的一个点移动的距离就是油桶滚动的距离。我们可以来看圆心,它移动的距离应该是16.2-0.5=15.7(米)(如图),所以要将这个油桶滚到墙边滚动的距离是15.7米。
则如果要将这个油桶滚到墙边,需要滚动15.7÷3.14=5(圈)。
10.r =1.72÷(4-3.14)=2正方形的面积:2×4=8(平方厘米)
圆的面积:3.14×2=6.28(平方厘米)
提示:外方内圆时,根据S阴=0.86r ,可先求出r 是多少。
7
/
7
