24.4.2 切线的判定与性质(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.4.2 切线的判定与性质(基础达标+巩固提升+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 09:01:23 | ||
图片预览


文档简介
沪科版数学九年级下册同步课时训练
第24章 圆
24.4 直线与圆的位置关系
第2课时 切线的性质与判定
要点测评 基础达标
要点1 切线的性质及其应用
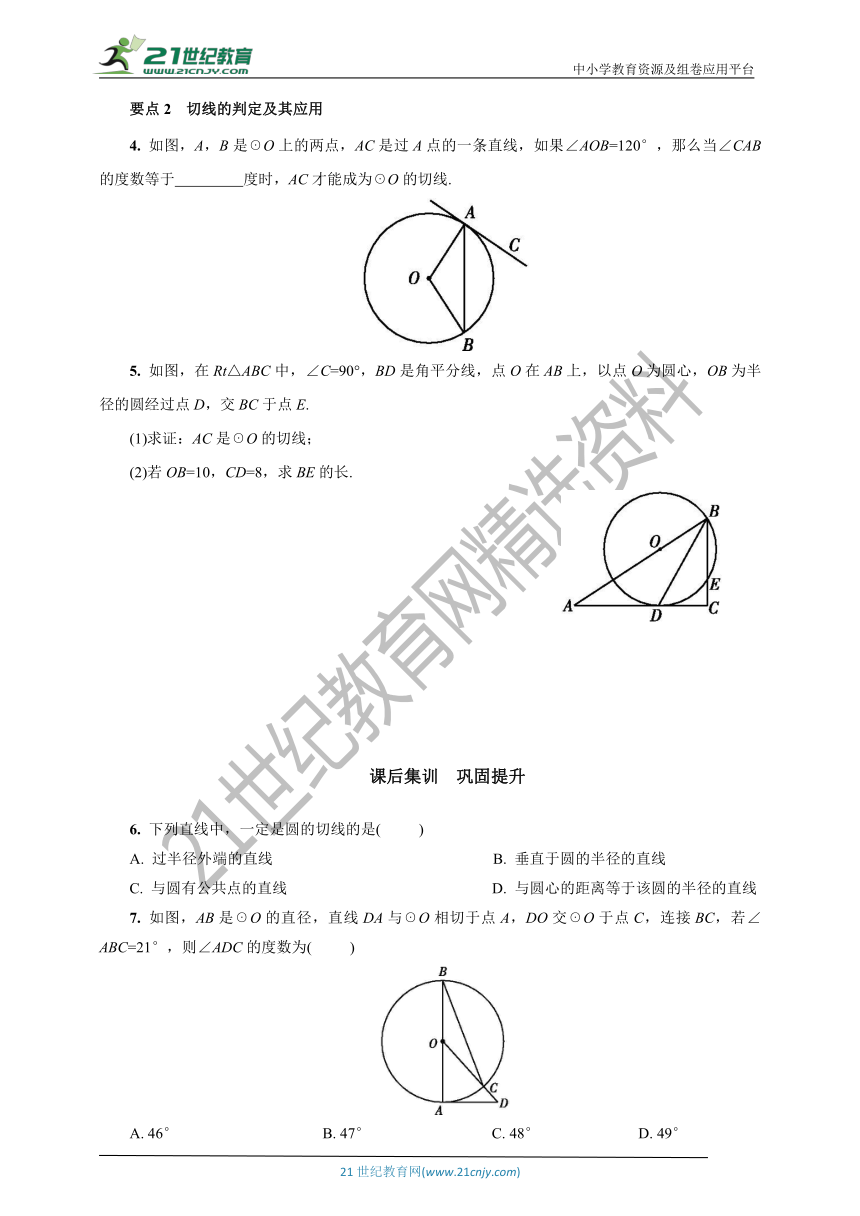
1. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A. 25° B. 40° C. 50° D. 65°
2. 如图所示,☉M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是 .?
3. 如图,过☉O上的两点A,B分别作切线,并交BO,AO的延长线于点C,D,连接CD,交☉O于点E,F,过圆心O作OM⊥CD,垂足为M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.
要点2 切线的判定及其应用
4. 如图,A,B是☉O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为☉O的切线.
5. 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是☉O的切线;
(2)若OB=10,CD=8,求BE的长.
课后集训 巩固提升
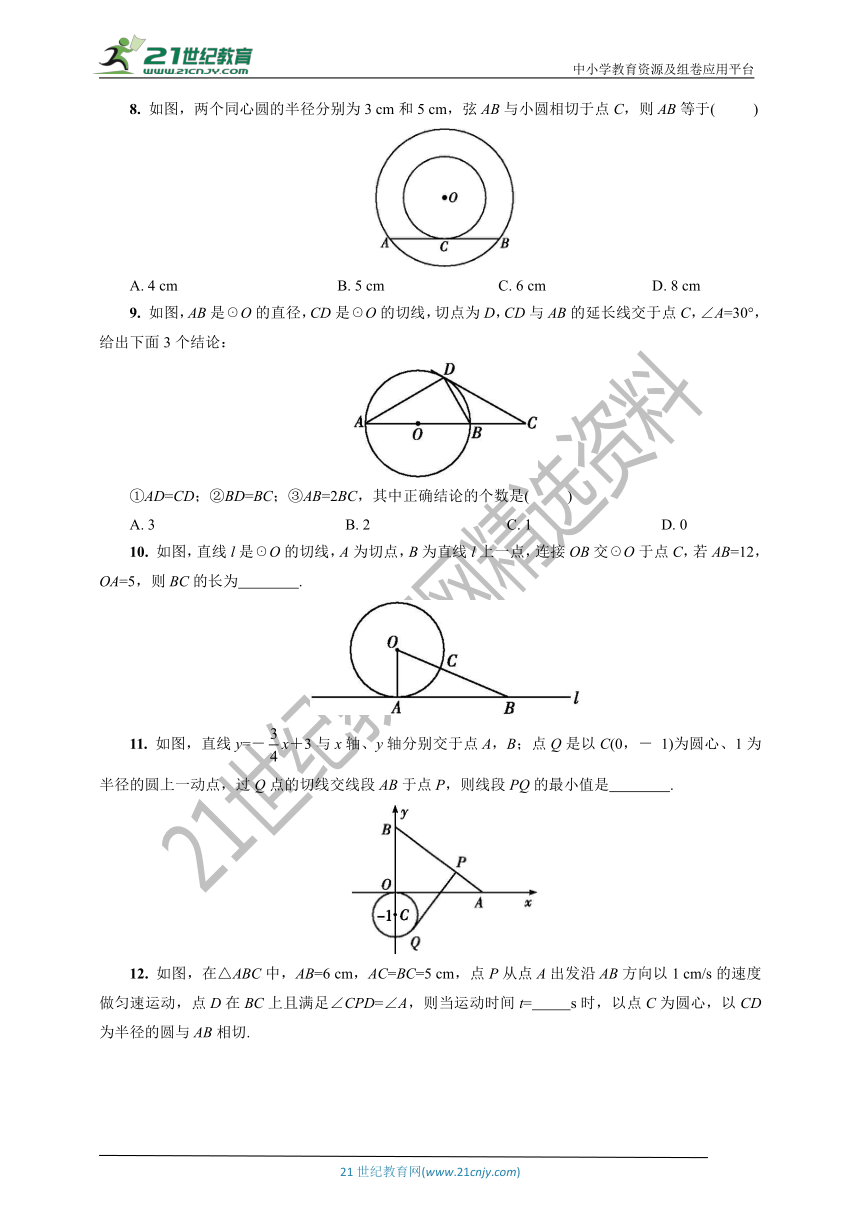
6. 下列直线中,一定是圆的切线的是( )
A. 过半径外端的直线 B. 垂直于圆的半径的直线
C. 与圆有公共点的直线 D. 与圆心的距离等于该圆的半径的直线
7. 如图,AB是☉O的直径,直线DA与☉O相切于点A,DO交☉O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
A. 46° B. 47° C. 48° D. 49°
8. 如图,两个同心圆的半径分别为3 cm和5 cm,弦AB与小圆相切于点C,则AB等于( )
A. 4 cm B. 5 cm C. 6 cm D. 8 cm
9. 如图,AB是☉O的直径,CD是☉O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:
①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A. 3 B. 2 C. 1 D. 0
10. 如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C,若AB=12,OA=5,则BC的长为 .
11. 如图,直线y=-x+3与x轴、y轴分别交于点A,B;点Q是以C(0,- 1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是 .
12. 如图,在△ABC中,AB=6 cm,AC=BC=5 cm,点P从点A出发沿AB方向以1 cm/s的速度做匀速运动,点D在BC上且满足∠CPD=∠A,则当运动时间t= s时,以点C为圆心,以CD为半径的圆与AB相切.
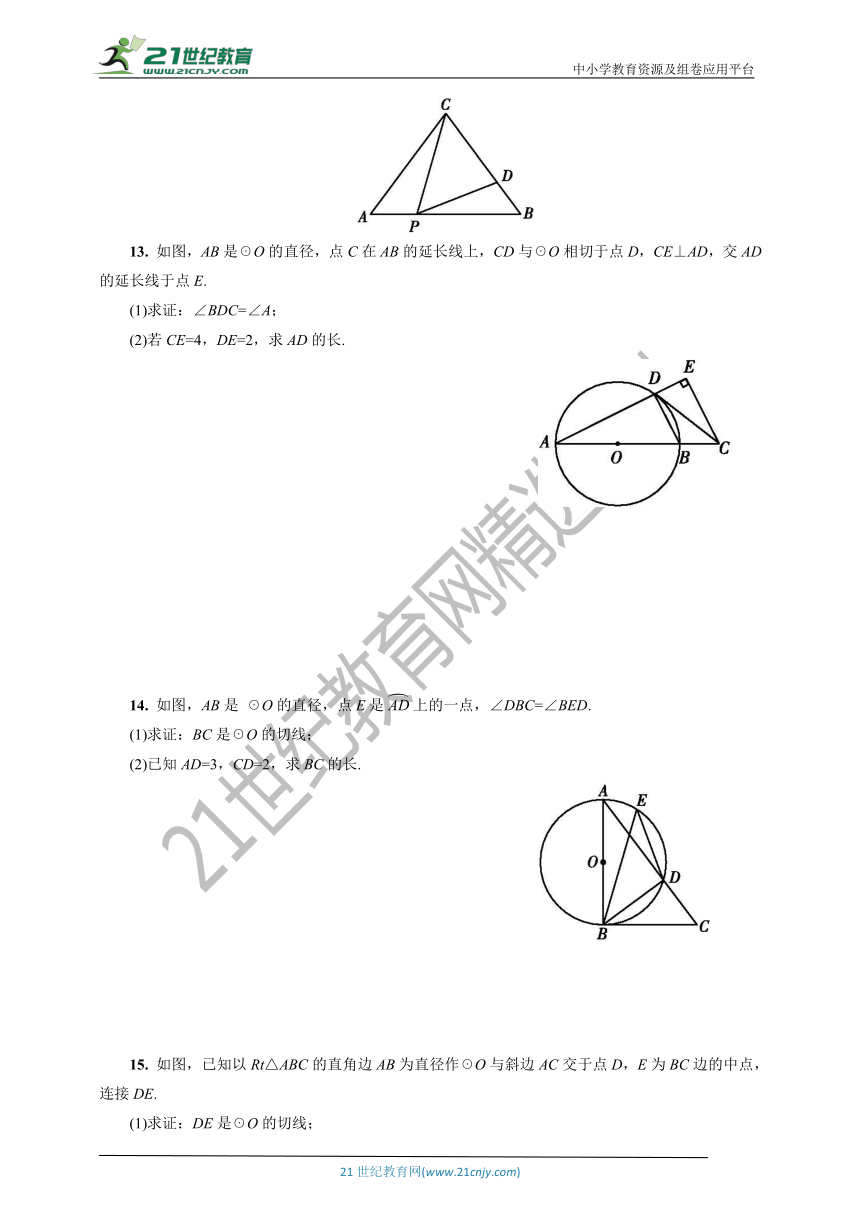
13. 如图,AB是☉O的直径,点C在AB的延长线上,CD与☉O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
14. 如图,AB是 ☉O的直径,点E是上的一点,∠DBC=∠BED.
(1)求证:BC是☉O的切线;
(2)已知AD=3,CD=2,求BC的长.
15. 如图,已知以Rt△ABC的直角边AB为直径作☉O与斜边AC交于点D,E为BC边的中点,连接DE.
(1)求证:DE是☉O的切线;
(2)连接OE,当∠CAB为何值时,四边形AOED是平行四边形;
(3)在(2)条件下探索四边形OBED的形状.
参 考 答 案
1. B 【解析】连接OC,因为圆O是Rt△ABC的外接圆,∠ACB=90°,所以AB是直径,因为∠A=25°,所以∠BOC=2∠A=50°,因为CD是圆O的切线,所以OC⊥CD,所以∠D=90°- ∠BOC=40°,故选B.
2. (5,4) 【解析】连接AM,作MN⊥x轴于点N.则AN=BN.因为点A(2,0),B(8,0),所以OA=2,OB=8,所以AB=OB- OA=6.所以AN=BN=3.所以ON=OA+AN=2+3=5,则点M的横坐标是5,圆的半径是5.在直角△AMN中,MN===4,则M的纵坐标是4.故M的坐标是(5,4).
3. 证明:(1)因为过☉O上的两点A,B分别作切线,所以∠CAO=∠DBO=90°,在△ACO和△BDO中因为所以△ACO≌△BDO(ASA).
(2)由(1)知△ACO≌△BDO,所以CO=DO,因为OM⊥CD,所以MC=DM,EM=MF,所以CE=DF.
4. 60 【解析】因为△AOB中,OA=OB,∠AOB=120°,所以∠OAB=30°,所以当∠CAB的度数等于60°时,OA⊥AC,AC才能成为☉O的切线.
5. (1)证明:连接OD,如图,因为BD为∠ABC的平分线,所以∠1=∠2,因为OB=OD,所以∠1=∠3,所以∠2=∠3,所以OD∥BC,因为∠C=90°,所以∠ODA=90°,则AC是圆O的切线.
(2)解:过O作OG⊥BC,连接OE,则四边形ODCG为矩形,所以GC=OD=OB=10,OG=CD=8,在Rt△OBG中,利用勾股定理得BG=6,因为OG⊥BE,OB=OE,所以BE=2BG=12.
6. D 【解析】根据切线的定义和判定定理知:与圆只有一个公共点的直线是圆的切线,到圆心的距离等于半径的直线是圆的切线,经过半径的外端并且垂直于这条半径的直线是圆的切线.故A,B,C项不正确,D项正确.故选D.
7. C 【解析】因为直线DA与☉O相切,所以∠OAD=90°.因为∠AOD=2∠ABC=2×21°=42°,所以∠ADC=90°- ∠AOD=90°- 42°=48°.故选C.
8. D 【解析】连接OA,OC,因为AB与小圆相切,所以OC⊥AB,所以C为AB的中点,即AC=BC=AB,在Rt△AOC中,OA=5 cm,OC=3 cm,根据勾股定理得AC==4 cm,则AB=2AC=8 cm.故选D.
9. A 【解析】连接OD,因为CD是☉O的切线,所以OD⊥DC,因为OA=OD,所以∠ODA=∠A=30°,所以∠DOC=60°,所以∠C=30°,所以AD=CD,①正确;因为AB是☉O的直径,所以∠ADB=90°,所以∠ODB=60°,所以∠BDC=30°=∠C,所以BD=BC,②正确;又∠A=30°,∠ADB=90°,所以AB=2BD=2BC,③正确,故选A.
10. 8 【解析】由切线的性质得OA⊥AB,因为OA=5,AB=12,所以由勾股定理得BO=13,由圆的性质知OC=OA,所以BC=BO-OC=13-5=8.
11. 【解析】过点C作CP⊥直线AB于点P,过点P作☉C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.当x=0时,y=3,所以点B的坐标为(0,3);当y=0时,x=4,所以点A的坐标为(4,0).所以OA=4,OB=3,所以AB==5,所以sin B==.因为C(0,-1),所以BC=3-(-1)=4,所以CP=BC·sin B=.因为PQ为☉C的切线,所以∠CQP=90°,所以PQ==.
12. 1或5 【解析】作CE⊥AB于E,因为AB=6 cm,AC=BC=5 cm,所以AE=BE=3 cm,所以CE=4 cm,因为☉C与AB相切,所以CD=CE=4 cm,所以BD=5-4=1 cm,因为AC=BC,所以∠A=∠B,因为∠BPC=∠CPD+∠BPD=∠A+∠ACP,∠CPD=∠A,所以∠BPD=∠ACP,所以△PAC∽△DBP,所以=,即=,解得t1=1,t2=5.又t>0,6- t>0,所以013. (1)证明:连接OD,因为CD是☉O切线,所以∠ODC=90°,因为AB为☉O的直径,所以∠ADB=90°,所以∠BDC=∠ADO,因为OA=OD,所以∠ADO=∠A,所以∠BDC=∠A.
(2)解:因为CE⊥AE,所以∠E=∠ADB=90°,所以DB∥EC,所以∠DCE=∠BDC,因为∠BDC=∠A,所以∠A=∠DCE,所以△AEC∽△CED,所以=,所以EC2=DE·AE,所以16=2(2+AD),所以AD=6.
14. (1)证明:因为AB是☉O的直径,所以∠ADB=90°,又因为∠BAD=∠BED,∠BED=∠DBC,所以∠BAD=∠DBC,所以∠DBC+∠ABD=∠BAD+∠ABD=90°,所以∠ABC=90°,即OB⊥BC,所以BC是☉O的切线.
(2)解:因为∠BAD=∠DBC,∠C=∠C,所以△ABC∽△BDC,所以=,即BC2=AC·CD=(AD+CD)·CD=10,所以BC=.
15. (1)证明:连接OD,DB,因为AB是☉O的直径,所以∠ADB=90°,所以∠CDB=90°,因为E是BC边上的中点,所以CE=EB=DE,所以∠1=∠2,因为OB=OD,所以∠3=∠4,所以∠1+∠4=∠2+∠3,因为∠ABC=90°,所以∠EDO=90°,所以DE是☉O的切线.
(2)解:∠CAB=45°.理由如下:因为OA=OD,所以∠A=∠ODA=45°,所以∠DOA=180°- 45°- 45°=90°=∠EDO,所以DE∥AO,因为E为BC中点,OA=OB,所以EO∥AD,所以四边形AOED是平行四边形,即当∠CAB=45°时,四边形AOED是平行四边形.
(3)解:四边形OBED是正方形.理由如下:因为∠EDO=∠DOB=∠EBA=90°,OB=OD,所以四边形OBED是正方形.
第24章 圆
24.4 直线与圆的位置关系
第2课时 切线的性质与判定
要点测评 基础达标
要点1 切线的性质及其应用
1. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A. 25° B. 40° C. 50° D. 65°
2. 如图所示,☉M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是 .?
3. 如图,过☉O上的两点A,B分别作切线,并交BO,AO的延长线于点C,D,连接CD,交☉O于点E,F,过圆心O作OM⊥CD,垂足为M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.
要点2 切线的判定及其应用
4. 如图,A,B是☉O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于 度时,AC才能成为☉O的切线.
5. 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是☉O的切线;
(2)若OB=10,CD=8,求BE的长.
课后集训 巩固提升
6. 下列直线中,一定是圆的切线的是( )
A. 过半径外端的直线 B. 垂直于圆的半径的直线
C. 与圆有公共点的直线 D. 与圆心的距离等于该圆的半径的直线
7. 如图,AB是☉O的直径,直线DA与☉O相切于点A,DO交☉O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为( )
A. 46° B. 47° C. 48° D. 49°
8. 如图,两个同心圆的半径分别为3 cm和5 cm,弦AB与小圆相切于点C,则AB等于( )
A. 4 cm B. 5 cm C. 6 cm D. 8 cm
9. 如图,AB是☉O的直径,CD是☉O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:
①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
A. 3 B. 2 C. 1 D. 0
10. 如图,直线l是☉O的切线,A为切点,B为直线l上一点,连接OB交☉O于点C,若AB=12,OA=5,则BC的长为 .
11. 如图,直线y=-x+3与x轴、y轴分别交于点A,B;点Q是以C(0,- 1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是 .
12. 如图,在△ABC中,AB=6 cm,AC=BC=5 cm,点P从点A出发沿AB方向以1 cm/s的速度做匀速运动,点D在BC上且满足∠CPD=∠A,则当运动时间t= s时,以点C为圆心,以CD为半径的圆与AB相切.
13. 如图,AB是☉O的直径,点C在AB的延长线上,CD与☉O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
14. 如图,AB是 ☉O的直径,点E是上的一点,∠DBC=∠BED.
(1)求证:BC是☉O的切线;
(2)已知AD=3,CD=2,求BC的长.
15. 如图,已知以Rt△ABC的直角边AB为直径作☉O与斜边AC交于点D,E为BC边的中点,连接DE.
(1)求证:DE是☉O的切线;
(2)连接OE,当∠CAB为何值时,四边形AOED是平行四边形;
(3)在(2)条件下探索四边形OBED的形状.
参 考 答 案
1. B 【解析】连接OC,因为圆O是Rt△ABC的外接圆,∠ACB=90°,所以AB是直径,因为∠A=25°,所以∠BOC=2∠A=50°,因为CD是圆O的切线,所以OC⊥CD,所以∠D=90°- ∠BOC=40°,故选B.
2. (5,4) 【解析】连接AM,作MN⊥x轴于点N.则AN=BN.因为点A(2,0),B(8,0),所以OA=2,OB=8,所以AB=OB- OA=6.所以AN=BN=3.所以ON=OA+AN=2+3=5,则点M的横坐标是5,圆的半径是5.在直角△AMN中,MN===4,则M的纵坐标是4.故M的坐标是(5,4).
3. 证明:(1)因为过☉O上的两点A,B分别作切线,所以∠CAO=∠DBO=90°,在△ACO和△BDO中因为所以△ACO≌△BDO(ASA).
(2)由(1)知△ACO≌△BDO,所以CO=DO,因为OM⊥CD,所以MC=DM,EM=MF,所以CE=DF.
4. 60 【解析】因为△AOB中,OA=OB,∠AOB=120°,所以∠OAB=30°,所以当∠CAB的度数等于60°时,OA⊥AC,AC才能成为☉O的切线.
5. (1)证明:连接OD,如图,因为BD为∠ABC的平分线,所以∠1=∠2,因为OB=OD,所以∠1=∠3,所以∠2=∠3,所以OD∥BC,因为∠C=90°,所以∠ODA=90°,则AC是圆O的切线.
(2)解:过O作OG⊥BC,连接OE,则四边形ODCG为矩形,所以GC=OD=OB=10,OG=CD=8,在Rt△OBG中,利用勾股定理得BG=6,因为OG⊥BE,OB=OE,所以BE=2BG=12.
6. D 【解析】根据切线的定义和判定定理知:与圆只有一个公共点的直线是圆的切线,到圆心的距离等于半径的直线是圆的切线,经过半径的外端并且垂直于这条半径的直线是圆的切线.故A,B,C项不正确,D项正确.故选D.
7. C 【解析】因为直线DA与☉O相切,所以∠OAD=90°.因为∠AOD=2∠ABC=2×21°=42°,所以∠ADC=90°- ∠AOD=90°- 42°=48°.故选C.
8. D 【解析】连接OA,OC,因为AB与小圆相切,所以OC⊥AB,所以C为AB的中点,即AC=BC=AB,在Rt△AOC中,OA=5 cm,OC=3 cm,根据勾股定理得AC==4 cm,则AB=2AC=8 cm.故选D.
9. A 【解析】连接OD,因为CD是☉O的切线,所以OD⊥DC,因为OA=OD,所以∠ODA=∠A=30°,所以∠DOC=60°,所以∠C=30°,所以AD=CD,①正确;因为AB是☉O的直径,所以∠ADB=90°,所以∠ODB=60°,所以∠BDC=30°=∠C,所以BD=BC,②正确;又∠A=30°,∠ADB=90°,所以AB=2BD=2BC,③正确,故选A.
10. 8 【解析】由切线的性质得OA⊥AB,因为OA=5,AB=12,所以由勾股定理得BO=13,由圆的性质知OC=OA,所以BC=BO-OC=13-5=8.
11. 【解析】过点C作CP⊥直线AB于点P,过点P作☉C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.当x=0时,y=3,所以点B的坐标为(0,3);当y=0时,x=4,所以点A的坐标为(4,0).所以OA=4,OB=3,所以AB==5,所以sin B==.因为C(0,-1),所以BC=3-(-1)=4,所以CP=BC·sin B=.因为PQ为☉C的切线,所以∠CQP=90°,所以PQ==.
12. 1或5 【解析】作CE⊥AB于E,因为AB=6 cm,AC=BC=5 cm,所以AE=BE=3 cm,所以CE=4 cm,因为☉C与AB相切,所以CD=CE=4 cm,所以BD=5-4=1 cm,因为AC=BC,所以∠A=∠B,因为∠BPC=∠CPD+∠BPD=∠A+∠ACP,∠CPD=∠A,所以∠BPD=∠ACP,所以△PAC∽△DBP,所以=,即=,解得t1=1,t2=5.又t>0,6- t>0,所以0
(2)解:因为CE⊥AE,所以∠E=∠ADB=90°,所以DB∥EC,所以∠DCE=∠BDC,因为∠BDC=∠A,所以∠A=∠DCE,所以△AEC∽△CED,所以=,所以EC2=DE·AE,所以16=2(2+AD),所以AD=6.
14. (1)证明:因为AB是☉O的直径,所以∠ADB=90°,又因为∠BAD=∠BED,∠BED=∠DBC,所以∠BAD=∠DBC,所以∠DBC+∠ABD=∠BAD+∠ABD=90°,所以∠ABC=90°,即OB⊥BC,所以BC是☉O的切线.
(2)解:因为∠BAD=∠DBC,∠C=∠C,所以△ABC∽△BDC,所以=,即BC2=AC·CD=(AD+CD)·CD=10,所以BC=.
15. (1)证明:连接OD,DB,因为AB是☉O的直径,所以∠ADB=90°,所以∠CDB=90°,因为E是BC边上的中点,所以CE=EB=DE,所以∠1=∠2,因为OB=OD,所以∠3=∠4,所以∠1+∠4=∠2+∠3,因为∠ABC=90°,所以∠EDO=90°,所以DE是☉O的切线.
(2)解:∠CAB=45°.理由如下:因为OA=OD,所以∠A=∠ODA=45°,所以∠DOA=180°- 45°- 45°=90°=∠EDO,所以DE∥AO,因为E为BC中点,OA=OB,所以EO∥AD,所以四边形AOED是平行四边形,即当∠CAB=45°时,四边形AOED是平行四边形.
(3)解:四边形OBED是正方形.理由如下:因为∠EDO=∠DOB=∠EBA=90°,OB=OD,所以四边形OBED是正方形.
