2020版高考艺考生文化课百日冲刺 第24讲 空间几何体的平行与垂直(课件:82张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第24讲 空间几何体的平行与垂直(课件:82张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览









文档简介
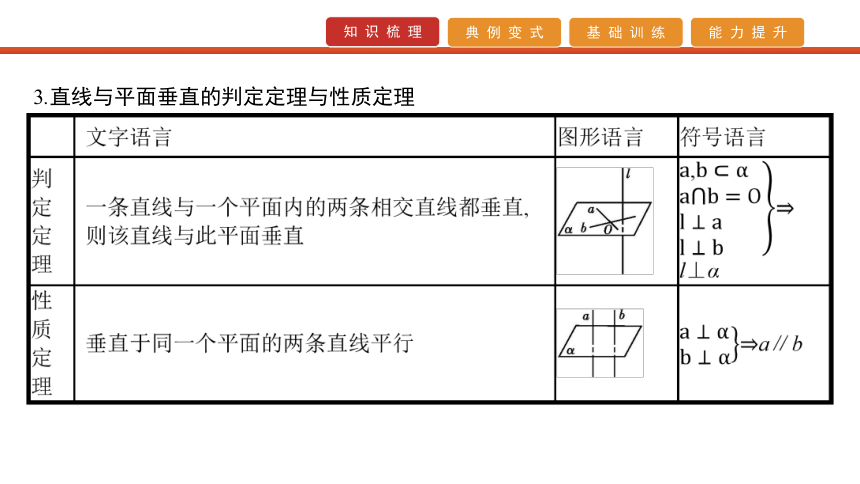
课件82张PPT。第24讲 空间几何体的平行与垂直1.直线与平面平行的判定定理和性质定理 2.平面与平面平行的判定定理和性质定理 3.直线与平面垂直的判定定理与性质定理 4.平面与平面垂直的判定定理与性质定理 题型一 空间线面位置关系的判定与异面直线所成的角
【例1-1】 (1)设α,β是两个不同的平面,m是直线且m?α,“m∥β”是“α∥β”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
(2)(教材改编)设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m(3)设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若m?α,n∥α,则m∥n;
②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若α∩β=n,m∥n,m∥α,则m∥β;
④若α⊥γ,β⊥γ,则α∥β.
其中是真命题的是 .(填上序号)?【解析】 (1)当m∥β时,过m的平面α与β可能平行也可能相交,因而m∥β ?/ α∥β;当α∥β时,α内任一直线与β平行,因为m?α,所以m∥β.综上知,“m∥β”是“α∥β”的必要而不充分条件.
(2)∵l⊥β,l?α,∴α⊥β(面面垂直的判定定理),故A正确.
(3)对于①,m∥n或m,n异面,故①错误;易知②正确;对于③,m∥β或m?β,故③错误;对于④,α∥β或α与β相交,故④错误.
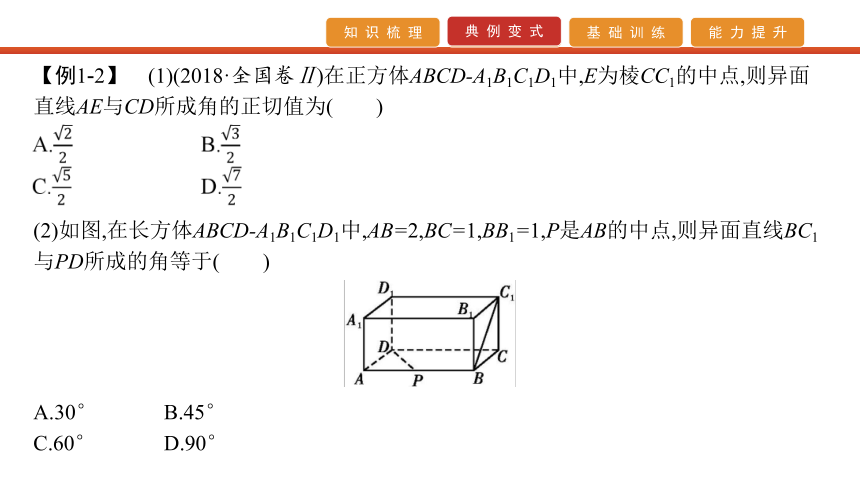
【答案】(1)B (2)A (3)②【例1-2】 (1)(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )(2)如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成的角等于( )A.30° B.45°
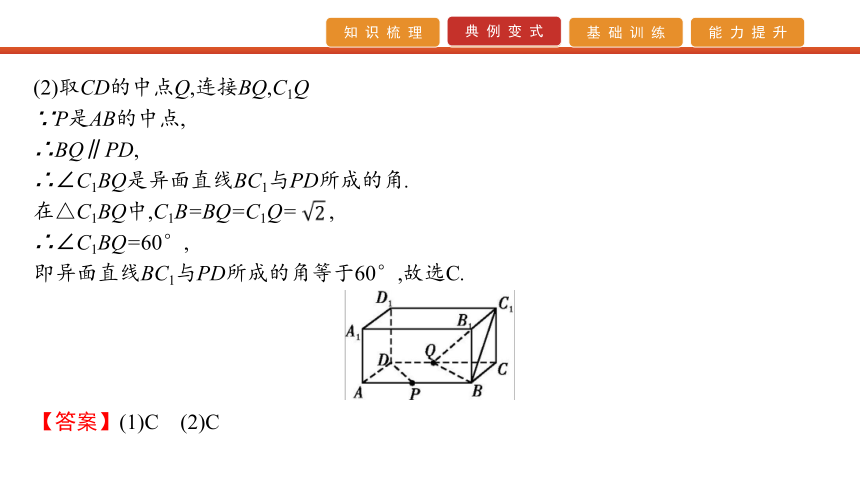
C.60° D.90°【解析】 (1)如图,连接BE,因为AB∥CD,所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角,即∠EAB.不妨设正方体的棱长为2,则CE=1,BC=2,由勾股定(2)取CD的中点Q,连接BQ,C1Q
∵P是AB的中点,
∴BQ∥PD,
∴∠C1BQ是异面直线BC1与PD所成的角.
在△C1BQ中,C1B=BQ=C1Q= ,
∴∠C1BQ=60°,
即异面直线BC1与PD所成的角等于60°,故选C.【答案】(1)C (2)C 【规律方法】用平移法求异面直线所成的角的步骤
(1)一作:根据定义作平行线,作出异面直线所成的角;
(2)二证:证明作出的角是异面直线所成的角;
(3)三求:解三角形,求出作出的角.如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角.变式训练一
1.已知m,n表示不同的直线,α,β表示不同的平面,下列命题为真的是( )
A.若m∥α,m⊥n,则n⊥α
B.若m∥α,α⊥β,则m⊥β
C.若m∥n,n∥α,则m∥α
D.若α∥β,m∥n,m⊥α,则n⊥βD 【解析】 当m∥α,m⊥n时,n与α的位置关系有n?α,或n∥α或n与α相交,故A不正确.
当m∥α,α⊥β时,m与β的位置关系有m?β或m∥β或m与β相交,故B不正确.
当m∥n,n∥α时,有m?α或m∥α,故C不正确.
当α∥β,m∥n,m⊥α时,必有n⊥β,故D正确.2.已知直线a和平面α,β,α∩β=l,a?α,a?β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是( )
A.相交或平行
B.相交或异面
C.平行或异面
D.相交、平行或异面D 【解析】 依题意,直线b和c的位置关系可能是相交、平行或异面,选D.3.如图,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为 (把你认为正确的结论的序号都填上).?③④ 【解析】 直线AM与CC1是异面直线,直线AM与BN也是异面直线,故①②错误.4.(1)已知P是△ABC所在平面外的一点,M,N分别是AB、PC的中点,若MN=BC=4, PA=4 ,则异面直线PA与MN所成角的大小是( )
A.30° B.45°
C.60° D.90°A (2)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为 .?【解析】 (1)取AC的中点O,连接OM,ON,则 ∴∠ONM=30°
即异面直线PA与MN所成角的大小为30°,故选A.(2)取圆柱下底面弧AB的另一中点D,连接C1D,AD,
因为C是圆柱下底面弧AB的中点,所以AD∥BC,
所以直线AC1与AD所成角等于异面直线AC1与BC所成角,因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD.题型二 空间平行、垂直关系的证明 BC,DC,SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.证明:(1)如图,连接SB, ∵E,G分别是BC,SC的中点,
∴EG∥SB.
又∵SB?平面BDD1B1,
EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.(2)连接SD,
∵F,G分别是DC,SC的中点,
∴FG∥SD.
又∵SD?平面BDD1B1,FG?平面BDD1B1,
∴FG∥平面BDD1B1,由(1)知,
EG∥平面BDD1B1,且EG?平面EFG,
FG?平面EFG,EG∩FG=G,
∴平面EFG∥平面BDD1B1.【例2-2】 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
求证:(1)AF∥平面BCE;
(2)平面BCE⊥平面CDE.证明:(1)如图,取CE的中点G,连接FG,BG. ∵F为CD的中点,
∴GF∥DE且GF= DE.
∵AB⊥平面ACD,
DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.
又AB= DE,∴GF=AB.
∴四边形GFAB为平行四边形,
∴AF∥BG.
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE.(2)∵△ACD为等边三角形,F为CD的中点,
∴AF⊥CD.
∵DE⊥平面ACD,AF?平面ACD,
∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.【规律方法】
(1)平行
①证明线面平行时,先直观判断平面内是否存在一条直线和已知直线平行,若找不到这样的直线,可以考虑通过面面平行来推导线面平行.②应用线面平行性质的关键是如何确定交线的位置,有时需要经过已知直线作辅助平面来确定交线. ③利用平面几何知识证明线线平行的主要方法:有中点,找中点,连中线,证平行;构造三角形的中位线;构造平行四边形条件.(2)垂直 变式训练二
1.如图,四棱锥P-ABCD中,AD∥BC,AB=BC= AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
(1)求证:AP∥平面BEF;
(2)求证:GH∥平面PAD.证明: (1)连接EC,因为AD∥BC,BC= AD,
所以BC??AE,
所以四边形ABCE是平行四边形,所以O为AC的中点.
又因为F是PC的中点,
所以FO∥AP,
因为FO?平面BEF,AP?平面BEF,
所以AP∥平面BEF.(2)连接FH,OH,
因为F,H分别是PC,CD的中点,
所以FH∥PD,
所以FH∥平面PAD.
又因为O是AC的中点,H是CD的中点,所以OH∥AD,所以OH∥平面PAD.
又FH∩OH=H,
所以平面OHF∥平面PAD.
又因为GH?平面OHF,
所以GH∥平面PAD.2.如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2 .点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.解:(1)证明:因为BC∥平面GEFH,BC?平面PBC,
且平面PBC∩平面GEFH=GH,
所以GH∥BC.
同理可证EF∥BC,因此GH∥EF.
(2)如图,连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可得PO⊥BD.
又BD∩AC=O,且AC,BD都在底面内,
所以PO⊥底面ABCD.
又因为平面GEFH⊥平面ABCD,
且PO?平面GEFH,
所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,所以PO∥GK,且GK⊥底面ABCD,从而GK⊥EF.
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,3.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°, PA=AB=BC,E是PC的中点.证明:(1)CD⊥AE;
(2)PD⊥平面ABE.证明:(1)在四棱锥P-ABCD中,
因为PA⊥底面ABCD,CD?平面ABCD,
所以PA⊥CD.因为AC⊥CD,PA∩AC=A,
所以CD⊥平面PAC.
而AE?平面PAC,所以CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
由(1)知AE⊥CD,且PC∩CD=C,
所以AE⊥平面PCD.
而PD?平面PCD,
所以AE⊥PD.
因为PA⊥底面ABCD,所以PA⊥AB.
又因为AB⊥AD且PA∩AD=A,
所以AB⊥平面PAD,而PD?平面PAD,
所以AB⊥PD.又因为AB∩AE=A,
所以PD⊥平面ABE.4.如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.
求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.证明:(1)由题意知,E为B1C的中点,又D为AB1的中点,
因此DE∥AC.
又因为DE?平面AA1C1C,AC?平面AA1C1C,
所以DE∥平面AA1C1C.
(2)因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC?平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1?平面BCC1B1,
BC?平面BCC1B1,
BC∩CC1=C,
所以AC⊥平面BCC1B1,又因为BC1?平面BCC1B1,
所以BC1⊥AC.
因为BC=CC1,
所以矩形BCC1B1是正方形,
因此BC1⊥B1C.
因为AC?平面B1AC,B1C?平面B1AC,AC∩B1C=C,
所以BC1⊥平面B1AC.
又因为AB1?平面B1AC,
所以BC1⊥AB1.题型三 平面图形的折叠问题
【例3】 如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2). (1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?请说明理由.证明:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.
又因为DE?平面A1CB,BC?平面A1CB,
所以DE∥平面A1CB.
证明:(2)由题图(1)得AC⊥BC
且DE∥BC,
所以DE⊥AC.
所以DE⊥A1D,DE⊥CD.
所以DE⊥平面A1DC.
而A1F?平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,
所以A1F⊥平面BCDE,又BE?平面BCDE,所以A1F⊥BE.【解析】 (3)线段A1B上存在点Q,
使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,
所以DE∥PQ.
所以平面DEQ即为平面DEP.由(2)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.
所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
【规律方法】解决由平面图形翻折为空间图形问题的关键是看翻折前后线面位置关系的变化情况,根据翻折的过程,把翻折前后一些线线位置关系中没有变化和发生变化的量准确找出来,这些不变和变化的量反映了翻折后的空间图形的结构特征.变式训练三 AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE. 图1 图2
(1)证明:CD⊥平面A1OC;解:(1)证明:在题图1中,连接EC(图略), 即在题图2中,BE⊥A1O,BE⊥OC,
从而BE⊥平面A1OC.
又CD∥BE,所以CD⊥平面A1OC.(2)由已知,平面A1BE⊥平面BCDE,
且平面A1BE∩平面BCDE=BE,
又由(1)可得A1O⊥BE,所以A1O⊥平面BCDE.
即A1O是四棱锥A1-BCDE的高.题型四 空间中的平行、垂直综合问题
【例4】 (2015·山东卷)如图,三棱台DEF ABC中,AB=2DE,G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.证明:(1)方法一 如图,连接DG,设CD∩GF=M,连接MH. AB=2DE,G为AC的中点,
可得DF∥GC,DF=GC,
所以四边形DFCG为平行四边形.
则M为CD的中点,
又H为BC的中点,
所以HM∥BD,又HM?平面FGH,BD?平面FGH,
所以BD∥平面FGH.可得BH∥EF,BH=EF,
所以四边形HBEF为平行四边形,
可得BE∥HF.在△ABC中,G为AC的中点,
H为BC的中点,所以GH∥AB.
又GH∩HF=H,
所以平面FGH∥平面ABED.
又因为BD?平面ABED,
所以BD∥平面FGH.(2)连接HE, 因为G,H分别为AC,BC的中点,
所以GH∥AB.
由AB⊥BC,得GH⊥BC.
又H为BC的中点,
所以EF∥HC,EF=HC,
因此四边形EFCH是平行四边形,
所以CF∥HE.又CF⊥BC,所以HE⊥BC.又HE,GH?平面EGH,HE∩GH=H,
所以BC⊥平面EGH.
又BC?平面BCD,
所以平面BCD⊥平面EGH.
【规律方法】线线平行(垂直)、线面平行(垂直)和面面平行(垂直)是空间中三种基本平行(垂直)关系,它们之间可以相互转化,其转化关系如下:变式训练四
1.(2017·山东卷)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.证明:(1)取B1D1的中点O1,连接CO1,A1O1,
由于ABCD-A1B1C1D1是四棱柱,
所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,所以A1O∥O1C,
又O1C?平面B1CD1,A1O?平面B1CD1,
所以A1O∥平面B1CD1.
(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,
又A1E⊥平面ABCD,BD?平面ABCD,
所以A1E⊥BD,
所以EM⊥B1D1,A1E⊥B1D1,
又A1E,EM?平面A1EM,A1E∩EM=E,
所以B1D1⊥平面A1EM,又B1D1?平面B1CD1,
所以平面A1EM⊥平面B1CD1.2.(2017·北京卷)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.解:(1)证明:因为PA⊥AB,PA⊥BC,
所以PA⊥平面ABC.
又因为BD?平面ABC,
所以PA⊥BD.
(2)证明:因为AB=BC,D为AC的中点,
所以BD⊥AC.
由(1)知,PA⊥BD,
所以BD⊥平面PAC.
所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE,平面PAC∩平面BDE=DE,
所以PA∥DE.
因为D为AC的中点,由(1)知,PA⊥平面ABC,
所以DE⊥平面ABC.题型五 空间中的平行、垂直探索性问题
【例5】 如图,四棱锥P ABCD中,AB∥CD,AB=2CD,E为PB的中点.
(1)求证:CE∥平面PAD;
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论,若不存在,请说明理由.证明:(1)如图所示,取PA的中点H,连接EH,DH,
因为E为PB的中点,所以EH∥CD,EH=CD,
因此四边形DCEH是平行四边形,
所以CE∥DH,
又DH?平面PAD,CE?平面PAD,
所以CE∥平面PAD.又AF∥CD,所以四边形AFCD为平行四边形,所以CF∥AD,
又CF?平面PAD,所以CF∥平面PAD,由(1)可知CE∥平面PAD,
又CE∩CF=C,故平面CEF∥平面PAD,故存在AB的中点F满足要求.
【规律方法】解决探索性问题的策略方法
(1)根据探索性问题的设问,假设其存在并探索出结论,然后在这个假设下进行推理论证,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设.
(2)按类似于分析法的格式书写步骤:从结论出发“要使……成立”“只需使……成立”.变式训练五 (1)若F为BB1的中点,判断AC1与平面DEF是否平行?若平行, 请给予证明,若不平行,说明理由;解: (1)法一:连接B1C,BC1交于点G,连接DG,FG,
则DG∥AC1,因为DG?平面GDF,AC1?平面GDF,
则AC1∥平面GDF.由于平面GDF∩平面DEF=DF,故AC1与平面DEF不可能平行.
法二:连接B1C,BC1交于点G,连接DG,FG,
则DG∥AC1,而DG?平面DEF,且DG与平面DEF交于点D,故AC1与平面DEF不可能平行.
(2)假设点F存在,由1.若直线a∥平面α,直线b∥直线a,点A∈b且A∈α,则b与α的位置关系是( )
A.b∩α=A B.b∥α
C.b∥α或b?α D.b?αD 【解析】 由a∥α,b∥a?b∥α或b?α,又b过α内一点,故b?α. 2.(2019·长春模拟)设m,n是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )
A.若m⊥n,n∥α,则m⊥α
B.若m∥β,β⊥α,则m⊥α
C.若m⊥β,n⊥β,n⊥α,则m⊥α
D.若m⊥n,n⊥β,β⊥α,则m⊥αC 【解析】 A中,由m⊥n,n∥α可得m∥α或m与α相交或m⊥α,错误;
B中,由m∥β,β⊥α可得m∥α或m与α相交或m?α,错误;
C中,由m⊥β,n⊥β可得m∥n,又n⊥α,所以m⊥α,正确;
D中,由m⊥n,n⊥β,β⊥α可得m∥α或m与α相交或m?α,错误.3.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“a⊥b”是“α⊥β ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件B 【解析】 因为α⊥β,b⊥m,所以b⊥α,又直线a在平面α内,所以a⊥b;但直线a,m不一定相交,所以“a⊥b”是“α⊥β ”的必要不充分条件,故选B.4.在正方体ABCD A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是( )
A.相交 B.异面 C.平行 D.垂直A 【解析】 如图所示,直线A1B与直线外一点E确定的平面为A1BCD1,EF?平面A1BCD1,且两直线不平行,故两直线相交.5.已知l,m,n为不同的直线,α,β,γ为不同的平面,则下列结论正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n∥β,α⊥β,则m⊥n
C.若α∩β=l,m∥α,m∥β,则m∥l
D.若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥αC 【解析】 A.m,n可能的位置关系为平行,相交或异面,故A错误;B.根据面面垂直与线面平行的性质可知B错误;C.根据线面平行的性质可知C正确;D.若m∥n,根据线面垂直的判定可知D错误,故选C.6.已知ABCD为空间四边形,AB=CD,AD=BC,AB≠AD,M,N分别是对角线AC与BD的中点,则MN与( )
A.AC,BD之一垂直 B.AC,BD都垂直
C.AC,BD都不垂直 D.AC,BD不一定垂直B 【解析】 ∵AD=BC,AB=CD,BD=BD,
∴△ABD≌△CDB,连接AN,CN,则AN=CN.
在等腰△ANC中,由M为AC的中点知MN⊥AC.
同理可得MN⊥BD.7.(2019·黄山模拟)E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1D 【解析】 如图,设B1C∩BC1=O,
可得平面D1BC1∩平面B1CE=EO,
∵BD1∥平面B1CE,根据线面平行的性质可得D1B∥EO,
∵O为B1C的中点,∴E为C1D1中点,∴D1E=EC1,故选D.8.已知正方体ABCD-A1B1C1D1的棱长为2,点P是平面AA1D1D的中心,点Q是上底面A1B1C1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长的最小值为( )A 【解析】 由PQ∥平面AA1B1B知Q在过点P且平行于平面AA1B1B的平面上,易知点Q在A1D1,B1C1中点的连线MN上,故PQ的最小值为PM= AA1=1.9.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?平行四边形 【解析】 ∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,
∴EF∥HG.同理EH∥FG,
∴四边形EFGH的形状是平行四边形.10.如图,在三棱锥S-ABC中,已知点D,E,F分别为棱AC,SA,SC的中点.
(1)求证:EF∥平面ABC;
(2)若SA=SC,BA=BC,求证:平面SBD⊥平面ABC.【证明】(1)∵EF是△SAC的中位线,
∴EF∥AC.
又EF?平面ABC,AC?平面ABC,
∴EF∥平面ABC.
(2)∵SA=SC,D是AC的中点,∴SD⊥AC.
∵BA=BC,D是AC的中点,∴BD⊥AC.
又SD?平面SBD,BD?平面SBD,SD∩DB=D,
∴AC⊥平面SBD.
又AC?平面ABC,
∴平面SBD⊥平面ABC.1.在四面体ABCD中,截面PQMN是正方形,则在下列结论中,错误的是( )A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°C 【解析】 因为截面PQMN是正方形,
所以MN∥PQ,则MN∥平面ABC,
由线面平行的性质知MN∥AC,
则AC∥截面PQMN,
同理可得MQ∥BD,又MN⊥QM,
则AC⊥BD,故A,B正确.
又因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,
故D正确.2.如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂
足.设AK=t,则t的取值范围是 .?【解析】 如图,过D作DG⊥AF,垂足为G,连接GK.
∵平面ABD⊥平面ABCF,又DK⊥AB,∴DK⊥平面ABCF,∴DK⊥AF.∵DK∩DG=D,
∴AF⊥平面DKG,∴AF⊥GK.
法一:易知当F接近点E时,K接近AB的中点,当F接近点C时,K接近AB的四等分点,法二:即在平面图形中,D,G,K三点共线,
设∠FAK=θ,则∠ADK=θ,AK=ADtan θ=tan θ,(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.【证明】(1)在△CDE中, 在四棱锥P-ABCE中,连接AC,
∵AE=2,∠AEC=60°,∴在△PAE中,PA2+AE2=PE2,
即AP⊥AE.
同理,AP⊥AC.而AC?平面ABCE,
AE?平面ABCE,AC∩AE=A,
故AP⊥平面ABCE.(2)∵AB∥CE,且CE?平面PCE,AB?平面PCE,
∴AB∥平面PCE.
又平面PAB∩平面PCE=l,∴AB∥l.4.在直三棱柱ABC-A1B1C1中,AC=2BC=2AA1=4,∠ACB=60°,E,F分别是A1C1,BC的中点.
(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P-B1C1F的体积.解:(1)证明:在△ABC中,∵AC=2BC=4,∠ACB=60°,
∴AB=2 ,∴AB2+BC2=AC2,∴AB⊥BC.
由已知AB⊥BB1,且BC∩BB1=B,
可得AB⊥平面BB1C1C.
又AB?平面ABE,∴平面ABE⊥平面BB1C1C.(2)证明:取AC的中点M,连接C1M,FM,
在△ABC中,FM∥AB,
而FM?平面ABE,AB?平面ABE,
∴FM∥平面ABE,
在矩形ACC1A1中,E,M分别是A1C1,AC的中点,
∴C1M∥AE,
而C1M?平面ABE,AE?平面ABE,
∴C1M∥平面ABE,
∵C1M∩FM=M,∴平面ABE∥平面FMC1,
又C1F?平面FMC1,
故C1F∥平面ABE.(3)取B1C1的中点H,连接EH, 又AB⊥平面BB1C1C,∴EH⊥平面BB1C1C,
∵P是BE的中点,
【例1-1】 (1)设α,β是两个不同的平面,m是直线且m?α,“m∥β”是“α∥β”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
(2)(教材改编)设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m(3)设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若m?α,n∥α,则m∥n;
②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若α∩β=n,m∥n,m∥α,则m∥β;
④若α⊥γ,β⊥γ,则α∥β.
其中是真命题的是 .(填上序号)?【解析】 (1)当m∥β时,过m的平面α与β可能平行也可能相交,因而m∥β ?/ α∥β;当α∥β时,α内任一直线与β平行,因为m?α,所以m∥β.综上知,“m∥β”是“α∥β”的必要而不充分条件.
(2)∵l⊥β,l?α,∴α⊥β(面面垂直的判定定理),故A正确.
(3)对于①,m∥n或m,n异面,故①错误;易知②正确;对于③,m∥β或m?β,故③错误;对于④,α∥β或α与β相交,故④错误.
【答案】(1)B (2)A (3)②【例1-2】 (1)(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )(2)如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成的角等于( )A.30° B.45°
C.60° D.90°【解析】 (1)如图,连接BE,因为AB∥CD,所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角,即∠EAB.不妨设正方体的棱长为2,则CE=1,BC=2,由勾股定(2)取CD的中点Q,连接BQ,C1Q
∵P是AB的中点,
∴BQ∥PD,
∴∠C1BQ是异面直线BC1与PD所成的角.
在△C1BQ中,C1B=BQ=C1Q= ,
∴∠C1BQ=60°,
即异面直线BC1与PD所成的角等于60°,故选C.【答案】(1)C (2)C 【规律方法】用平移法求异面直线所成的角的步骤
(1)一作:根据定义作平行线,作出异面直线所成的角;
(2)二证:证明作出的角是异面直线所成的角;
(3)三求:解三角形,求出作出的角.如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角.变式训练一
1.已知m,n表示不同的直线,α,β表示不同的平面,下列命题为真的是( )
A.若m∥α,m⊥n,则n⊥α
B.若m∥α,α⊥β,则m⊥β
C.若m∥n,n∥α,则m∥α
D.若α∥β,m∥n,m⊥α,则n⊥βD 【解析】 当m∥α,m⊥n时,n与α的位置关系有n?α,或n∥α或n与α相交,故A不正确.
当m∥α,α⊥β时,m与β的位置关系有m?β或m∥β或m与β相交,故B不正确.
当m∥n,n∥α时,有m?α或m∥α,故C不正确.
当α∥β,m∥n,m⊥α时,必有n⊥β,故D正确.2.已知直线a和平面α,β,α∩β=l,a?α,a?β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是( )
A.相交或平行
B.相交或异面
C.平行或异面
D.相交、平行或异面D 【解析】 依题意,直线b和c的位置关系可能是相交、平行或异面,选D.3.如图,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为 (把你认为正确的结论的序号都填上).?③④ 【解析】 直线AM与CC1是异面直线,直线AM与BN也是异面直线,故①②错误.4.(1)已知P是△ABC所在平面外的一点,M,N分别是AB、PC的中点,若MN=BC=4, PA=4 ,则异面直线PA与MN所成角的大小是( )
A.30° B.45°
C.60° D.90°A (2)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为 .?【解析】 (1)取AC的中点O,连接OM,ON,则 ∴∠ONM=30°
即异面直线PA与MN所成角的大小为30°,故选A.(2)取圆柱下底面弧AB的另一中点D,连接C1D,AD,
因为C是圆柱下底面弧AB的中点,所以AD∥BC,
所以直线AC1与AD所成角等于异面直线AC1与BC所成角,因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD.题型二 空间平行、垂直关系的证明 BC,DC,SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.证明:(1)如图,连接SB, ∵E,G分别是BC,SC的中点,
∴EG∥SB.
又∵SB?平面BDD1B1,
EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.(2)连接SD,
∵F,G分别是DC,SC的中点,
∴FG∥SD.
又∵SD?平面BDD1B1,FG?平面BDD1B1,
∴FG∥平面BDD1B1,由(1)知,
EG∥平面BDD1B1,且EG?平面EFG,
FG?平面EFG,EG∩FG=G,
∴平面EFG∥平面BDD1B1.【例2-2】 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
求证:(1)AF∥平面BCE;
(2)平面BCE⊥平面CDE.证明:(1)如图,取CE的中点G,连接FG,BG. ∵F为CD的中点,
∴GF∥DE且GF= DE.
∵AB⊥平面ACD,
DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.
又AB= DE,∴GF=AB.
∴四边形GFAB为平行四边形,
∴AF∥BG.
∵AF?平面BCE,BG?平面BCE,
∴AF∥平面BCE.(2)∵△ACD为等边三角形,F为CD的中点,
∴AF⊥CD.
∵DE⊥平面ACD,AF?平面ACD,
∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE.【规律方法】
(1)平行
①证明线面平行时,先直观判断平面内是否存在一条直线和已知直线平行,若找不到这样的直线,可以考虑通过面面平行来推导线面平行.②应用线面平行性质的关键是如何确定交线的位置,有时需要经过已知直线作辅助平面来确定交线. ③利用平面几何知识证明线线平行的主要方法:有中点,找中点,连中线,证平行;构造三角形的中位线;构造平行四边形条件.(2)垂直 变式训练二
1.如图,四棱锥P-ABCD中,AD∥BC,AB=BC= AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
(1)求证:AP∥平面BEF;
(2)求证:GH∥平面PAD.证明: (1)连接EC,因为AD∥BC,BC= AD,
所以BC??AE,
所以四边形ABCE是平行四边形,所以O为AC的中点.
又因为F是PC的中点,
所以FO∥AP,
因为FO?平面BEF,AP?平面BEF,
所以AP∥平面BEF.(2)连接FH,OH,
因为F,H分别是PC,CD的中点,
所以FH∥PD,
所以FH∥平面PAD.
又因为O是AC的中点,H是CD的中点,所以OH∥AD,所以OH∥平面PAD.
又FH∩OH=H,
所以平面OHF∥平面PAD.
又因为GH?平面OHF,
所以GH∥平面PAD.2.如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2 .点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.解:(1)证明:因为BC∥平面GEFH,BC?平面PBC,
且平面PBC∩平面GEFH=GH,
所以GH∥BC.
同理可证EF∥BC,因此GH∥EF.
(2)如图,连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可得PO⊥BD.
又BD∩AC=O,且AC,BD都在底面内,
所以PO⊥底面ABCD.
又因为平面GEFH⊥平面ABCD,
且PO?平面GEFH,
所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,所以PO∥GK,且GK⊥底面ABCD,从而GK⊥EF.
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,3.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°, PA=AB=BC,E是PC的中点.证明:(1)CD⊥AE;
(2)PD⊥平面ABE.证明:(1)在四棱锥P-ABCD中,
因为PA⊥底面ABCD,CD?平面ABCD,
所以PA⊥CD.因为AC⊥CD,PA∩AC=A,
所以CD⊥平面PAC.
而AE?平面PAC,所以CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
由(1)知AE⊥CD,且PC∩CD=C,
所以AE⊥平面PCD.
而PD?平面PCD,
所以AE⊥PD.
因为PA⊥底面ABCD,所以PA⊥AB.
又因为AB⊥AD且PA∩AD=A,
所以AB⊥平面PAD,而PD?平面PAD,
所以AB⊥PD.又因为AB∩AE=A,
所以PD⊥平面ABE.4.如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.
求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.证明:(1)由题意知,E为B1C的中点,又D为AB1的中点,
因此DE∥AC.
又因为DE?平面AA1C1C,AC?平面AA1C1C,
所以DE∥平面AA1C1C.
(2)因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC?平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1?平面BCC1B1,
BC?平面BCC1B1,
BC∩CC1=C,
所以AC⊥平面BCC1B1,又因为BC1?平面BCC1B1,
所以BC1⊥AC.
因为BC=CC1,
所以矩形BCC1B1是正方形,
因此BC1⊥B1C.
因为AC?平面B1AC,B1C?平面B1AC,AC∩B1C=C,
所以BC1⊥平面B1AC.
又因为AB1?平面B1AC,
所以BC1⊥AB1.题型三 平面图形的折叠问题
【例3】 如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2). (1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?请说明理由.证明:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.
又因为DE?平面A1CB,BC?平面A1CB,
所以DE∥平面A1CB.
证明:(2)由题图(1)得AC⊥BC
且DE∥BC,
所以DE⊥AC.
所以DE⊥A1D,DE⊥CD.
所以DE⊥平面A1DC.
而A1F?平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,
所以A1F⊥平面BCDE,又BE?平面BCDE,所以A1F⊥BE.【解析】 (3)线段A1B上存在点Q,
使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,
所以DE∥PQ.
所以平面DEQ即为平面DEP.由(2)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.
所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
【规律方法】解决由平面图形翻折为空间图形问题的关键是看翻折前后线面位置关系的变化情况,根据翻折的过程,把翻折前后一些线线位置关系中没有变化和发生变化的量准确找出来,这些不变和变化的量反映了翻折后的空间图形的结构特征.变式训练三 AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE. 图1 图2
(1)证明:CD⊥平面A1OC;解:(1)证明:在题图1中,连接EC(图略), 即在题图2中,BE⊥A1O,BE⊥OC,
从而BE⊥平面A1OC.
又CD∥BE,所以CD⊥平面A1OC.(2)由已知,平面A1BE⊥平面BCDE,
且平面A1BE∩平面BCDE=BE,
又由(1)可得A1O⊥BE,所以A1O⊥平面BCDE.
即A1O是四棱锥A1-BCDE的高.题型四 空间中的平行、垂直综合问题
【例4】 (2015·山东卷)如图,三棱台DEF ABC中,AB=2DE,G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.证明:(1)方法一 如图,连接DG,设CD∩GF=M,连接MH. AB=2DE,G为AC的中点,
可得DF∥GC,DF=GC,
所以四边形DFCG为平行四边形.
则M为CD的中点,
又H为BC的中点,
所以HM∥BD,又HM?平面FGH,BD?平面FGH,
所以BD∥平面FGH.可得BH∥EF,BH=EF,
所以四边形HBEF为平行四边形,
可得BE∥HF.在△ABC中,G为AC的中点,
H为BC的中点,所以GH∥AB.
又GH∩HF=H,
所以平面FGH∥平面ABED.
又因为BD?平面ABED,
所以BD∥平面FGH.(2)连接HE, 因为G,H分别为AC,BC的中点,
所以GH∥AB.
由AB⊥BC,得GH⊥BC.
又H为BC的中点,
所以EF∥HC,EF=HC,
因此四边形EFCH是平行四边形,
所以CF∥HE.又CF⊥BC,所以HE⊥BC.又HE,GH?平面EGH,HE∩GH=H,
所以BC⊥平面EGH.
又BC?平面BCD,
所以平面BCD⊥平面EGH.
【规律方法】线线平行(垂直)、线面平行(垂直)和面面平行(垂直)是空间中三种基本平行(垂直)关系,它们之间可以相互转化,其转化关系如下:变式训练四
1.(2017·山东卷)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.证明:(1)取B1D1的中点O1,连接CO1,A1O1,
由于ABCD-A1B1C1D1是四棱柱,
所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,所以A1O∥O1C,
又O1C?平面B1CD1,A1O?平面B1CD1,
所以A1O∥平面B1CD1.
(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,
又A1E⊥平面ABCD,BD?平面ABCD,
所以A1E⊥BD,
所以EM⊥B1D1,A1E⊥B1D1,
又A1E,EM?平面A1EM,A1E∩EM=E,
所以B1D1⊥平面A1EM,又B1D1?平面B1CD1,
所以平面A1EM⊥平面B1CD1.2.(2017·北京卷)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.解:(1)证明:因为PA⊥AB,PA⊥BC,
所以PA⊥平面ABC.
又因为BD?平面ABC,
所以PA⊥BD.
(2)证明:因为AB=BC,D为AC的中点,
所以BD⊥AC.
由(1)知,PA⊥BD,
所以BD⊥平面PAC.
所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE,平面PAC∩平面BDE=DE,
所以PA∥DE.
因为D为AC的中点,由(1)知,PA⊥平面ABC,
所以DE⊥平面ABC.题型五 空间中的平行、垂直探索性问题
【例5】 如图,四棱锥P ABCD中,AB∥CD,AB=2CD,E为PB的中点.
(1)求证:CE∥平面PAD;
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论,若不存在,请说明理由.证明:(1)如图所示,取PA的中点H,连接EH,DH,
因为E为PB的中点,所以EH∥CD,EH=CD,
因此四边形DCEH是平行四边形,
所以CE∥DH,
又DH?平面PAD,CE?平面PAD,
所以CE∥平面PAD.又AF∥CD,所以四边形AFCD为平行四边形,所以CF∥AD,
又CF?平面PAD,所以CF∥平面PAD,由(1)可知CE∥平面PAD,
又CE∩CF=C,故平面CEF∥平面PAD,故存在AB的中点F满足要求.
【规律方法】解决探索性问题的策略方法
(1)根据探索性问题的设问,假设其存在并探索出结论,然后在这个假设下进行推理论证,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设.
(2)按类似于分析法的格式书写步骤:从结论出发“要使……成立”“只需使……成立”.变式训练五 (1)若F为BB1的中点,判断AC1与平面DEF是否平行?若平行, 请给予证明,若不平行,说明理由;解: (1)法一:连接B1C,BC1交于点G,连接DG,FG,
则DG∥AC1,因为DG?平面GDF,AC1?平面GDF,
则AC1∥平面GDF.由于平面GDF∩平面DEF=DF,故AC1与平面DEF不可能平行.
法二:连接B1C,BC1交于点G,连接DG,FG,
则DG∥AC1,而DG?平面DEF,且DG与平面DEF交于点D,故AC1与平面DEF不可能平行.
(2)假设点F存在,由1.若直线a∥平面α,直线b∥直线a,点A∈b且A∈α,则b与α的位置关系是( )
A.b∩α=A B.b∥α
C.b∥α或b?α D.b?αD 【解析】 由a∥α,b∥a?b∥α或b?α,又b过α内一点,故b?α. 2.(2019·长春模拟)设m,n是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )
A.若m⊥n,n∥α,则m⊥α
B.若m∥β,β⊥α,则m⊥α
C.若m⊥β,n⊥β,n⊥α,则m⊥α
D.若m⊥n,n⊥β,β⊥α,则m⊥αC 【解析】 A中,由m⊥n,n∥α可得m∥α或m与α相交或m⊥α,错误;
B中,由m∥β,β⊥α可得m∥α或m与α相交或m?α,错误;
C中,由m⊥β,n⊥β可得m∥n,又n⊥α,所以m⊥α,正确;
D中,由m⊥n,n⊥β,β⊥α可得m∥α或m与α相交或m?α,错误.3.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“a⊥b”是“α⊥β ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件B 【解析】 因为α⊥β,b⊥m,所以b⊥α,又直线a在平面α内,所以a⊥b;但直线a,m不一定相交,所以“a⊥b”是“α⊥β ”的必要不充分条件,故选B.4.在正方体ABCD A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是( )
A.相交 B.异面 C.平行 D.垂直A 【解析】 如图所示,直线A1B与直线外一点E确定的平面为A1BCD1,EF?平面A1BCD1,且两直线不平行,故两直线相交.5.已知l,m,n为不同的直线,α,β,γ为不同的平面,则下列结论正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n∥β,α⊥β,则m⊥n
C.若α∩β=l,m∥α,m∥β,则m∥l
D.若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥αC 【解析】 A.m,n可能的位置关系为平行,相交或异面,故A错误;B.根据面面垂直与线面平行的性质可知B错误;C.根据线面平行的性质可知C正确;D.若m∥n,根据线面垂直的判定可知D错误,故选C.6.已知ABCD为空间四边形,AB=CD,AD=BC,AB≠AD,M,N分别是对角线AC与BD的中点,则MN与( )
A.AC,BD之一垂直 B.AC,BD都垂直
C.AC,BD都不垂直 D.AC,BD不一定垂直B 【解析】 ∵AD=BC,AB=CD,BD=BD,
∴△ABD≌△CDB,连接AN,CN,则AN=CN.
在等腰△ANC中,由M为AC的中点知MN⊥AC.
同理可得MN⊥BD.7.(2019·黄山模拟)E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则( )
A.BD1∥CE
B.AC1⊥BD1
C.D1E=2EC1
D.D1E=EC1D 【解析】 如图,设B1C∩BC1=O,
可得平面D1BC1∩平面B1CE=EO,
∵BD1∥平面B1CE,根据线面平行的性质可得D1B∥EO,
∵O为B1C的中点,∴E为C1D1中点,∴D1E=EC1,故选D.8.已知正方体ABCD-A1B1C1D1的棱长为2,点P是平面AA1D1D的中心,点Q是上底面A1B1C1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长的最小值为( )A 【解析】 由PQ∥平面AA1B1B知Q在过点P且平行于平面AA1B1B的平面上,易知点Q在A1D1,B1C1中点的连线MN上,故PQ的最小值为PM= AA1=1.9.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?平行四边形 【解析】 ∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,
∴EF∥HG.同理EH∥FG,
∴四边形EFGH的形状是平行四边形.10.如图,在三棱锥S-ABC中,已知点D,E,F分别为棱AC,SA,SC的中点.
(1)求证:EF∥平面ABC;
(2)若SA=SC,BA=BC,求证:平面SBD⊥平面ABC.【证明】(1)∵EF是△SAC的中位线,
∴EF∥AC.
又EF?平面ABC,AC?平面ABC,
∴EF∥平面ABC.
(2)∵SA=SC,D是AC的中点,∴SD⊥AC.
∵BA=BC,D是AC的中点,∴BD⊥AC.
又SD?平面SBD,BD?平面SBD,SD∩DB=D,
∴AC⊥平面SBD.
又AC?平面ABC,
∴平面SBD⊥平面ABC.1.在四面体ABCD中,截面PQMN是正方形,则在下列结论中,错误的是( )A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°C 【解析】 因为截面PQMN是正方形,
所以MN∥PQ,则MN∥平面ABC,
由线面平行的性质知MN∥AC,
则AC∥截面PQMN,
同理可得MQ∥BD,又MN⊥QM,
则AC⊥BD,故A,B正确.
又因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,
故D正确.2.如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂
足.设AK=t,则t的取值范围是 .?【解析】 如图,过D作DG⊥AF,垂足为G,连接GK.
∵平面ABD⊥平面ABCF,又DK⊥AB,∴DK⊥平面ABCF,∴DK⊥AF.∵DK∩DG=D,
∴AF⊥平面DKG,∴AF⊥GK.
法一:易知当F接近点E时,K接近AB的中点,当F接近点C时,K接近AB的四等分点,法二:即在平面图形中,D,G,K三点共线,
设∠FAK=θ,则∠ADK=θ,AK=ADtan θ=tan θ,(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.【证明】(1)在△CDE中, 在四棱锥P-ABCE中,连接AC,
∵AE=2,∠AEC=60°,∴在△PAE中,PA2+AE2=PE2,
即AP⊥AE.
同理,AP⊥AC.而AC?平面ABCE,
AE?平面ABCE,AC∩AE=A,
故AP⊥平面ABCE.(2)∵AB∥CE,且CE?平面PCE,AB?平面PCE,
∴AB∥平面PCE.
又平面PAB∩平面PCE=l,∴AB∥l.4.在直三棱柱ABC-A1B1C1中,AC=2BC=2AA1=4,∠ACB=60°,E,F分别是A1C1,BC的中点.
(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P-B1C1F的体积.解:(1)证明:在△ABC中,∵AC=2BC=4,∠ACB=60°,
∴AB=2 ,∴AB2+BC2=AC2,∴AB⊥BC.
由已知AB⊥BB1,且BC∩BB1=B,
可得AB⊥平面BB1C1C.
又AB?平面ABE,∴平面ABE⊥平面BB1C1C.(2)证明:取AC的中点M,连接C1M,FM,
在△ABC中,FM∥AB,
而FM?平面ABE,AB?平面ABE,
∴FM∥平面ABE,
在矩形ACC1A1中,E,M分别是A1C1,AC的中点,
∴C1M∥AE,
而C1M?平面ABE,AE?平面ABE,
∴C1M∥平面ABE,
∵C1M∩FM=M,∴平面ABE∥平面FMC1,
又C1F?平面FMC1,
故C1F∥平面ABE.(3)取B1C1的中点H,连接EH, 又AB⊥平面BB1C1C,∴EH⊥平面BB1C1C,
∵P是BE的中点,
同课章节目录
