2020版高考艺考生文化课百日冲刺 第23讲 空间几何体的三视图及表面积与体积(课件:58张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第23讲 空间几何体的三视图及表面积与体积(课件:58张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 12:39:08 | ||
图片预览








文档简介
课件58张PPT。第23讲 空间几何体的三视图及表面积与体积1.柱体、锥体、台体、球的结构特征
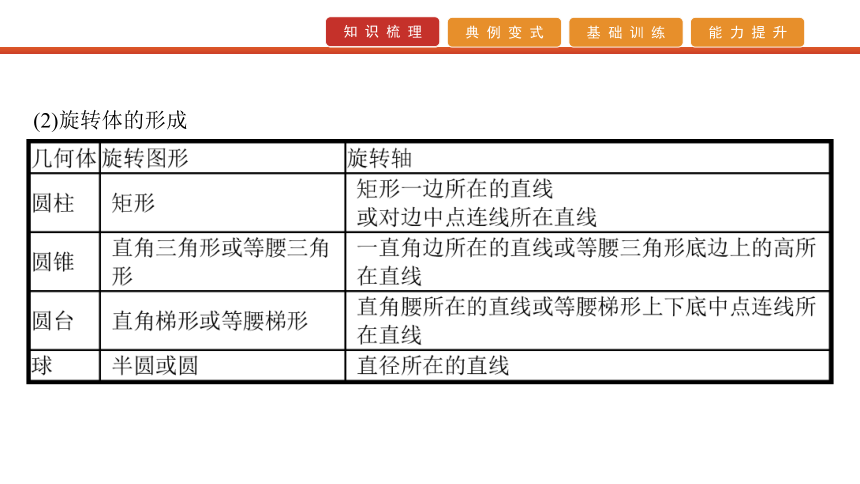
(1)多面体的结构特征 (2)旋转体的形成 2.柱体、锥体、台体、球的表面积与体积
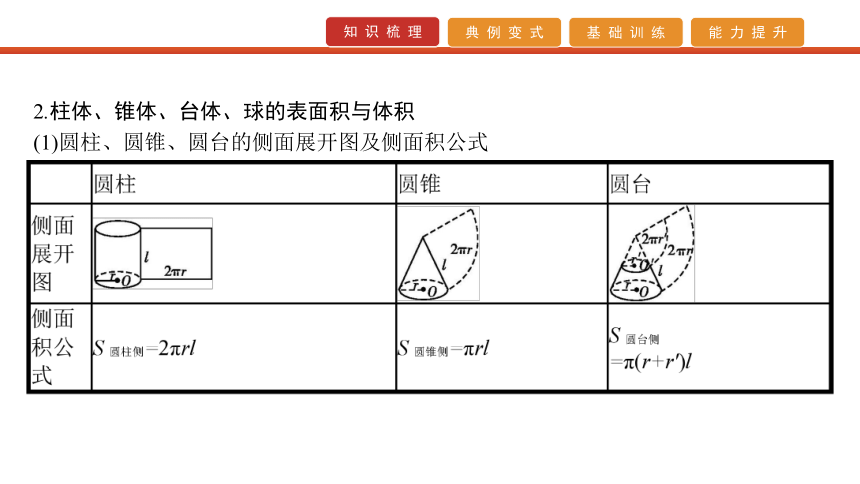
(1)圆柱、圆锥、圆台的侧面展开图及侧面积公式(2)空间几何体的表面积与体积公式 3.三视图
(1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.
(2)三视图的画法
①基本要求:长对正,高平齐,宽相等.
②画法规则:正侧一样高,正俯一样长,侧俯一样宽;看不到的线画虚线.
4.直观图
(1)画法:常用斜二测画法.
(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x'轴,y'轴的夹角为45°(或135°),z'轴与x'轴和y'轴所在平面垂直.
②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.5.求空间几何体体积的常用方法
①公式法:直接根据相关的体积公式计算.
②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.
③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.题型一 空间几何体的三视图(高频考点)
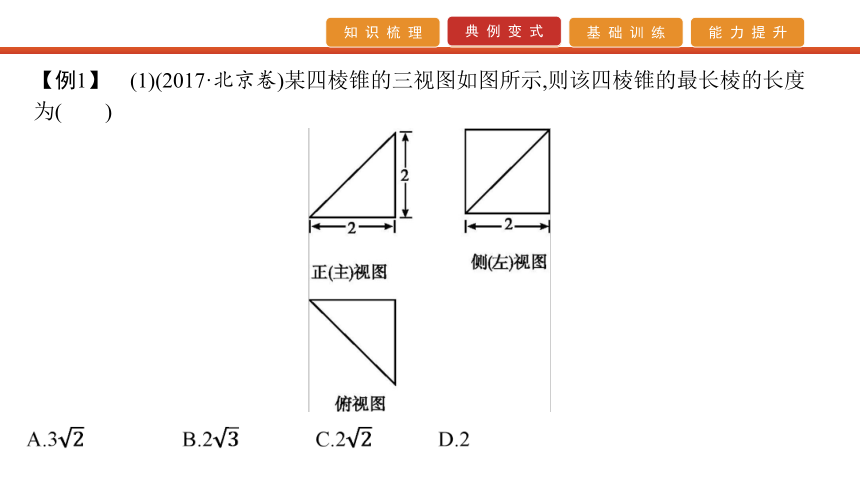
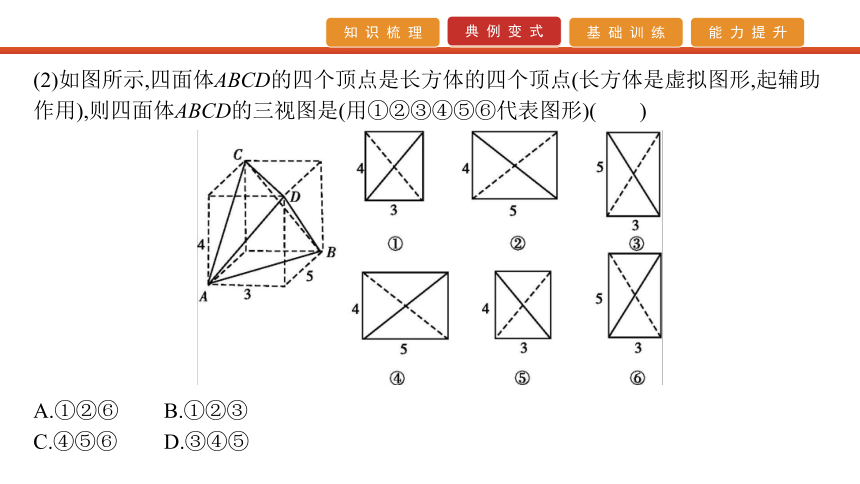
空间几何体的三视图是每年高考的热点,可以单独考查,也常与表面积、体积综合考查.主要命题角度有:①已知几何体,识别三视图;②已知三视图,判断几何体;③已知几何体的某些视图,判断其他视图.【例1】 (1)(2017·北京卷)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )(2)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )A.①②⑥ B.①②③
C.④⑤⑥ D.③④⑤【解析】 (1)由三视图还原为如图所示的四棱锥A-BCC1B1, 从图中易得最长的棱长为 (2)正视图应该是相邻两边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图应该是相邻两边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图是②;俯视图应该是相邻两边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③,故选B.
【答案】 (1)B (2)B【规律方法】三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的视图.先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.变式训练一
1.正方体ABCD-A1B1C1D1中,E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( ) A B C D C 【解析】 过点A,E,C1的截面为AEC1F,如图,则剩余几何体的侧视图为选项C中的图形,故选C.2.某几何体的三视图如图所示,那么这个几何体是( ) A.三棱锥 B.四棱锥
C.四棱台 D.三棱台A 【解析】 因为正视图和侧视图都为三角形,可知几何体为锥形,又因为俯视图为三角形,故该几何体为三棱锥.3.如图是一几何体的直观图、正视图和俯视图,则该几何体的侧视图为( ) A B C D B 【解析】 由三视图的画法规则:长对正、高平齐、宽相等可知,选项B正确. 题型二 空间几何体的直观图
【例2】 (1)已知正三角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为( )(2)如图,矩形O'A'B'C'是水平放置的一个平面图形的直观图,其中O'A'=6 cm,O'C'=2 cm,则原图形是( )A.正方形 B.矩形
C.菱形 D.一般的平行四边形【解析】 (1)如图①②所示的实 际图形和直观图,① ② 【答案】 (1)D (2)C 【规律方法】
(1)用斜二测画法画直观图的技巧:在原图形中与x轴或y轴平行的线段在直观图中与x'轴或y'轴平行,原图中不与坐标轴平行的直线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.(2)平面图形直观图与原图形面积间的关系:对于几何体的直观图,除掌握斜二测画法外,记住原图形面积S与直观图面积S'之间的关系S'= S,能更快捷地进行相关问题的计算.变式训练二
如图,一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积为 .?题型三 空间几何体的表面积和体积
【例3】 (1)从一个正方体中截去部分几何体,得到一个以原正方体的部分顶点为顶点的凸多面体,其三视图如图,则该几何体的体积为( )(2)(2018·太原模拟)某几何体的三视图如图所示,则该几何体的表面积等于( )【解析】 (1)由三视图知,该几何体为四棱锥B1-A1BCD1,如图所示,(2)由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为【答案】 (1)C (2)D
【规律方法】求空间几何体的体积的常用方法
(1)公式法:对于规则几何体的体积问题,可以直接利用公式进行求解.
(2)割补法:把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积.
(3)等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.变式训练三
1.一个多面体的三视图如图所示,则该多面体的表面积为( )A 【解析】 由三视图可得如图所示的几何体,
是棱长为2的正方体去掉对角上两个小三棱锥,故该多面体的表面积为S=6×2×2-2.一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )C 【解析】 由三视图可知,四棱锥的底面是边长为1的正方形,高为1,其体积 3.(2017·全国卷Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90π B.63π C.42π D.36π B 【解析】 由三视图可知两个同样的几何体可以拼成一个底面直径为6,高为14的圆柱,所以该几何体的体积V= ×32×π×14=63π.故选B.4.如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )A题型四 球与空间几何体的接、切问题(高频考点)
与球相关的切、接问题是高考命题的热点,也是难点、易失分点,命题角度多变.主要命题角度有:①外接球;②内切球.
考法一 外接球
【例4-1】 (1)(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )(2)(2018·全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9 ,则三棱锥D-ABC体积的最大值为( )【答案】(1)B (2)B 【解析】 (1)设圆柱的底面半径为r,球的半径为R,且R=1,由圆柱两个底面的圆周在同一个球的球面上可知,r,R及圆柱的高的一半构成直角三角形.考法二 内切球
【例4-2】 已知棱长为a的正四面体,则此正四面体的表面积S1与其内切球的表面积S2的比值为 .?【规律方法】空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.变式训练四
1.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC, AA1=12,则球O的半径为( )C 【解析】 由球心作平面ABC的垂线,则垂足为BC的中点M. 2.已知三棱锥S??ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2 , AB=1, AC=2,∠BAC=60°,则球O的表面积为( )
A.4π B.12π C.16π D.64πC 【解析】 在△ABC中,BC2=AB2+AC2-2AB·AC·cos 60°=3,
∴AC2=AB2+BC2,即AB⊥BC,又∵SA⊥平面ABC,故球O的表面积为4π×22=16π. 3.在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,△ABC,△ACD,△ABD的面积分别为【解析】 如图,以AB,AC,AD为棱把该三棱锥扩充成长方体,则该长方体的外接球恰为三棱锥的外接球,
∴三棱锥的外接球的直径是长方体的对角线长.4.如图,直三棱柱ABC?? A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )C 【解析】 由题意知,球心在侧面BCC1B1的中心O上,BC为截面圆的直径,∴∠BAC=90°,△ABC的外接圆圆心N位于BC的中点,同理△A1B1C1的外心M是B1C1的中点.1.将长方体截去一个四棱锥后得到的几何体如图所示,则该几何体的侧视图为( )D 【解析】 根据几何体的结构特征进行分析即可. 2.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为 ,则该几何体的俯视图可以是( ) A B C D C 【解析】 由正视图和侧视图及体积易得几何体是四棱锥P-ABCD,其中ABCD是边长为 3.已知正四棱锥的底面边长为2a,其侧视图如图所示.当正视图的面积最大时,该正四棱锥的表面积为( )B 【解析】 由题意可知该正四棱锥的直观图如图所示,其正视图与侧视图相同,设棱锥的 4.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是( )【解析】 由三视图可知,该几何体是两个同底的半圆锥,其中底的半径为1,高为 D 5.三棱锥S ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,SA=AB=BC=1,则球O的表面积为( )C 【解析】 如图,∵AB⊥BC,∴AC是△ABC所在截面圆的直径,
又∵SA⊥平面ABC,∴△SAC所在的截面圆是球的大圆,∴SC是球的一条直径.6.有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所
示),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为 .?【解析】 如图,在直观图中,过点A作AE⊥BC,垂足为E,
则在Rt△ABE中,AB=1,∠ABE=45°,7.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为 cm.?13 【解析】 如图,过点A作AC⊥OB,交OB于点C.
在Rt△ABC中,AC=12 cm,BC=8-3=5(cm).9.已知某几何体的三视图如下图所示,则该几何体的表面积为 .?母线长为2的圆锥的一半,其表面积是整个圆锥表面积的一半与轴截面的面积之和. 10.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.【解析】 (1)该几何体是一个正方体切掉两个 圆柱后得到的几何体.
(2)直观图如图所示.△AEF,则截面△AEF的周长的最小值为 .? 6 【解析】 沿着侧棱VA把正三棱锥V ABC展开在一个平面内,
如图,
则AA'即为截面△AEF周长的最小值,且∠AVA'=3×40°=120°.
在△VAA'中,由余弦定理可得AA'=6,故答案为6.2.已知矩形ABCD的面积为8,当矩形周长最小时,沿对角线AC把△ACD折起,则三棱16π 2,无论怎样折叠,其四个顶点都在一个半径为2的球面上,这个球的表面积是4π×22=16π. 3.(2018·福州综合质量检测)已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的
直径,△ABC是边长为4的等边三角形,三棱锥P-ABC的体积为 ,则此三棱锥的外接球
的表面积为( ) D 【解析】 依题意,记三棱锥P-ABC的外接球的球心为O,半径为R,点P到平面ABC的4.如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=30°.
(1)求证:EF⊥PB;(1)【证明】∵EF∥BC且BC⊥AB,
∴EF⊥AB,即EF⊥BE,EF⊥PE.又∵BE∩PE=E,
∴EF⊥平面PBE,又∵PB?平面PBE,
∴EF⊥PB.
(2)解:设BE=x,PE=y,则x+y=4.当且仅当x=y=2时,S△PEB的面积最大.
此时,BE=PE=2.
由(1)知EF⊥平面PBE,
∴平面PBE⊥平面EFCB,
在平面PBE中,作PO⊥BE于O,则PO⊥平面EFCB.即PO为四棱锥P EFCB的高.
(1)多面体的结构特征 (2)旋转体的形成 2.柱体、锥体、台体、球的表面积与体积
(1)圆柱、圆锥、圆台的侧面展开图及侧面积公式(2)空间几何体的表面积与体积公式 3.三视图
(1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.
(2)三视图的画法
①基本要求:长对正,高平齐,宽相等.
②画法规则:正侧一样高,正俯一样长,侧俯一样宽;看不到的线画虚线.
4.直观图
(1)画法:常用斜二测画法.
(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x'轴,y'轴的夹角为45°(或135°),z'轴与x'轴和y'轴所在平面垂直.
②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.5.求空间几何体体积的常用方法
①公式法:直接根据相关的体积公式计算.
②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.
③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.题型一 空间几何体的三视图(高频考点)
空间几何体的三视图是每年高考的热点,可以单独考查,也常与表面积、体积综合考查.主要命题角度有:①已知几何体,识别三视图;②已知三视图,判断几何体;③已知几何体的某些视图,判断其他视图.【例1】 (1)(2017·北京卷)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )(2)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )A.①②⑥ B.①②③
C.④⑤⑥ D.③④⑤【解析】 (1)由三视图还原为如图所示的四棱锥A-BCC1B1, 从图中易得最长的棱长为 (2)正视图应该是相邻两边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图应该是相邻两边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图是②;俯视图应该是相邻两边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③,故选B.
【答案】 (1)B (2)B【规律方法】三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的视图.先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.变式训练一
1.正方体ABCD-A1B1C1D1中,E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( ) A B C D C 【解析】 过点A,E,C1的截面为AEC1F,如图,则剩余几何体的侧视图为选项C中的图形,故选C.2.某几何体的三视图如图所示,那么这个几何体是( ) A.三棱锥 B.四棱锥
C.四棱台 D.三棱台A 【解析】 因为正视图和侧视图都为三角形,可知几何体为锥形,又因为俯视图为三角形,故该几何体为三棱锥.3.如图是一几何体的直观图、正视图和俯视图,则该几何体的侧视图为( ) A B C D B 【解析】 由三视图的画法规则:长对正、高平齐、宽相等可知,选项B正确. 题型二 空间几何体的直观图
【例2】 (1)已知正三角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为( )(2)如图,矩形O'A'B'C'是水平放置的一个平面图形的直观图,其中O'A'=6 cm,O'C'=2 cm,则原图形是( )A.正方形 B.矩形
C.菱形 D.一般的平行四边形【解析】 (1)如图①②所示的实 际图形和直观图,① ② 【答案】 (1)D (2)C 【规律方法】
(1)用斜二测画法画直观图的技巧:在原图形中与x轴或y轴平行的线段在直观图中与x'轴或y'轴平行,原图中不与坐标轴平行的直线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.(2)平面图形直观图与原图形面积间的关系:对于几何体的直观图,除掌握斜二测画法外,记住原图形面积S与直观图面积S'之间的关系S'= S,能更快捷地进行相关问题的计算.变式训练二
如图,一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积为 .?题型三 空间几何体的表面积和体积
【例3】 (1)从一个正方体中截去部分几何体,得到一个以原正方体的部分顶点为顶点的凸多面体,其三视图如图,则该几何体的体积为( )(2)(2018·太原模拟)某几何体的三视图如图所示,则该几何体的表面积等于( )【解析】 (1)由三视图知,该几何体为四棱锥B1-A1BCD1,如图所示,(2)由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为【答案】 (1)C (2)D
【规律方法】求空间几何体的体积的常用方法
(1)公式法:对于规则几何体的体积问题,可以直接利用公式进行求解.
(2)割补法:把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积.
(3)等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.变式训练三
1.一个多面体的三视图如图所示,则该多面体的表面积为( )A 【解析】 由三视图可得如图所示的几何体,
是棱长为2的正方体去掉对角上两个小三棱锥,故该多面体的表面积为S=6×2×2-2.一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )C 【解析】 由三视图可知,四棱锥的底面是边长为1的正方形,高为1,其体积 3.(2017·全国卷Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90π B.63π C.42π D.36π B 【解析】 由三视图可知两个同样的几何体可以拼成一个底面直径为6,高为14的圆柱,所以该几何体的体积V= ×32×π×14=63π.故选B.4.如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )A题型四 球与空间几何体的接、切问题(高频考点)
与球相关的切、接问题是高考命题的热点,也是难点、易失分点,命题角度多变.主要命题角度有:①外接球;②内切球.
考法一 外接球
【例4-1】 (1)(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )(2)(2018·全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9 ,则三棱锥D-ABC体积的最大值为( )【答案】(1)B (2)B 【解析】 (1)设圆柱的底面半径为r,球的半径为R,且R=1,由圆柱两个底面的圆周在同一个球的球面上可知,r,R及圆柱的高的一半构成直角三角形.考法二 内切球
【例4-2】 已知棱长为a的正四面体,则此正四面体的表面积S1与其内切球的表面积S2的比值为 .?【规律方法】空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.变式训练四
1.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC, AA1=12,则球O的半径为( )C 【解析】 由球心作平面ABC的垂线,则垂足为BC的中点M. 2.已知三棱锥S??ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2 , AB=1, AC=2,∠BAC=60°,则球O的表面积为( )
A.4π B.12π C.16π D.64πC 【解析】 在△ABC中,BC2=AB2+AC2-2AB·AC·cos 60°=3,
∴AC2=AB2+BC2,即AB⊥BC,又∵SA⊥平面ABC,故球O的表面积为4π×22=16π. 3.在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,△ABC,△ACD,△ABD的面积分别为【解析】 如图,以AB,AC,AD为棱把该三棱锥扩充成长方体,则该长方体的外接球恰为三棱锥的外接球,
∴三棱锥的外接球的直径是长方体的对角线长.4.如图,直三棱柱ABC?? A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )C 【解析】 由题意知,球心在侧面BCC1B1的中心O上,BC为截面圆的直径,∴∠BAC=90°,△ABC的外接圆圆心N位于BC的中点,同理△A1B1C1的外心M是B1C1的中点.1.将长方体截去一个四棱锥后得到的几何体如图所示,则该几何体的侧视图为( )D 【解析】 根据几何体的结构特征进行分析即可. 2.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为 ,则该几何体的俯视图可以是( ) A B C D C 【解析】 由正视图和侧视图及体积易得几何体是四棱锥P-ABCD,其中ABCD是边长为 3.已知正四棱锥的底面边长为2a,其侧视图如图所示.当正视图的面积最大时,该正四棱锥的表面积为( )B 【解析】 由题意可知该正四棱锥的直观图如图所示,其正视图与侧视图相同,设棱锥的 4.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是( )【解析】 由三视图可知,该几何体是两个同底的半圆锥,其中底的半径为1,高为 D 5.三棱锥S ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,SA=AB=BC=1,则球O的表面积为( )C 【解析】 如图,∵AB⊥BC,∴AC是△ABC所在截面圆的直径,
又∵SA⊥平面ABC,∴△SAC所在的截面圆是球的大圆,∴SC是球的一条直径.6.有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所
示),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为 .?【解析】 如图,在直观图中,过点A作AE⊥BC,垂足为E,
则在Rt△ABE中,AB=1,∠ABE=45°,7.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为 cm.?13 【解析】 如图,过点A作AC⊥OB,交OB于点C.
在Rt△ABC中,AC=12 cm,BC=8-3=5(cm).9.已知某几何体的三视图如下图所示,则该几何体的表面积为 .?母线长为2的圆锥的一半,其表面积是整个圆锥表面积的一半与轴截面的面积之和. 10.某几何体的三视图如图所示.
(1)判断该几何体是什么几何体?
(2)画出该几何体的直观图.【解析】 (1)该几何体是一个正方体切掉两个 圆柱后得到的几何体.
(2)直观图如图所示.△AEF,则截面△AEF的周长的最小值为 .? 6 【解析】 沿着侧棱VA把正三棱锥V ABC展开在一个平面内,
如图,
则AA'即为截面△AEF周长的最小值,且∠AVA'=3×40°=120°.
在△VAA'中,由余弦定理可得AA'=6,故答案为6.2.已知矩形ABCD的面积为8,当矩形周长最小时,沿对角线AC把△ACD折起,则三棱16π 2,无论怎样折叠,其四个顶点都在一个半径为2的球面上,这个球的表面积是4π×22=16π. 3.(2018·福州综合质量检测)已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的
直径,△ABC是边长为4的等边三角形,三棱锥P-ABC的体积为 ,则此三棱锥的外接球
的表面积为( ) D 【解析】 依题意,记三棱锥P-ABC的外接球的球心为O,半径为R,点P到平面ABC的4.如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=30°.
(1)求证:EF⊥PB;(1)【证明】∵EF∥BC且BC⊥AB,
∴EF⊥AB,即EF⊥BE,EF⊥PE.又∵BE∩PE=E,
∴EF⊥平面PBE,又∵PB?平面PBE,
∴EF⊥PB.
(2)解:设BE=x,PE=y,则x+y=4.当且仅当x=y=2时,S△PEB的面积最大.
此时,BE=PE=2.
由(1)知EF⊥平面PBE,
∴平面PBE⊥平面EFCB,
在平面PBE中,作PO⊥BE于O,则PO⊥平面EFCB.即PO为四棱锥P EFCB的高.
同课章节目录
