2020版高考艺考生文化课百日冲刺 第3讲 程序框图(课件:56张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第3讲 程序框图(课件:56张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览





文档简介
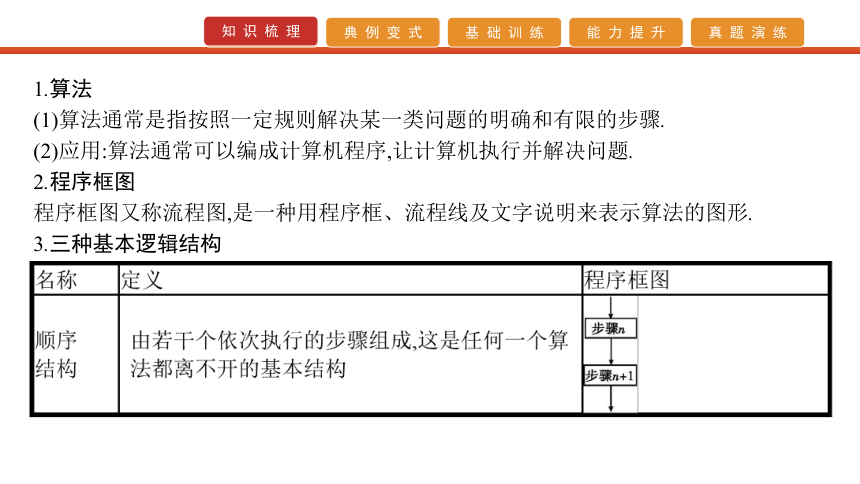
课件56张PPT。第3讲 程序框图1.算法
(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.
(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.
2.程序框图
程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.
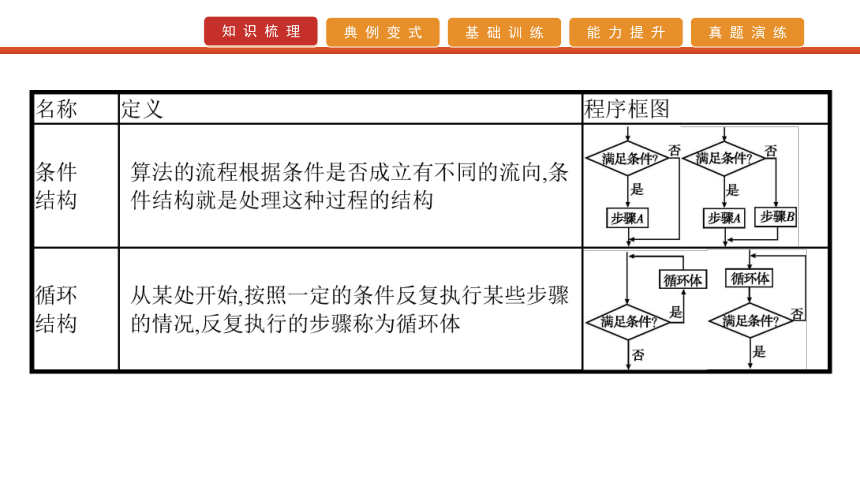
3.三种基本逻辑结构 题型一 程序框图的执行问题
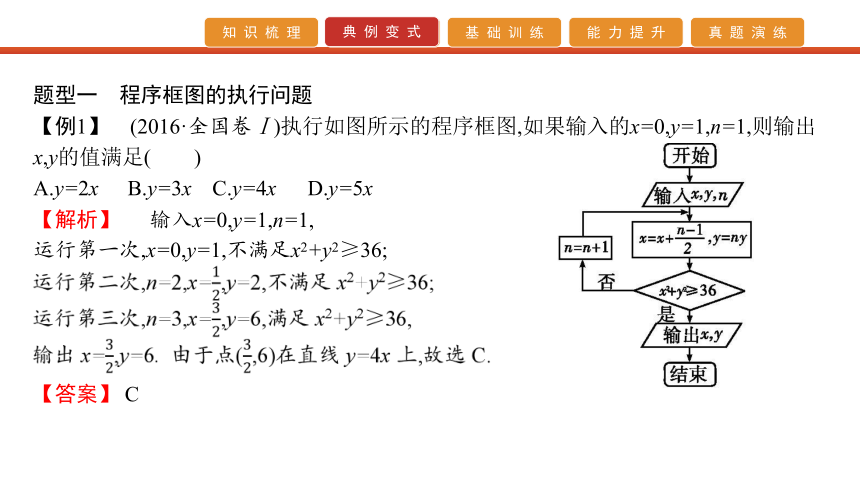
【例1】 (2016·全国卷Ⅰ)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x C.y=4x D.y=5x
【解析】 输入x=0,y=1,n=1,
运行第一次,x=0,y=1,不满足x2+y2≥36;【答案】 C【规律方法】利用循环结构表示算法的步骤
第一要先确定是利用当型循环结构,还是利用直到型循环结构;
第二要选择准确的表示累计的变量;
第三要注意在哪一步开始循环,满足什么条件不再执行循环体.变式训练一
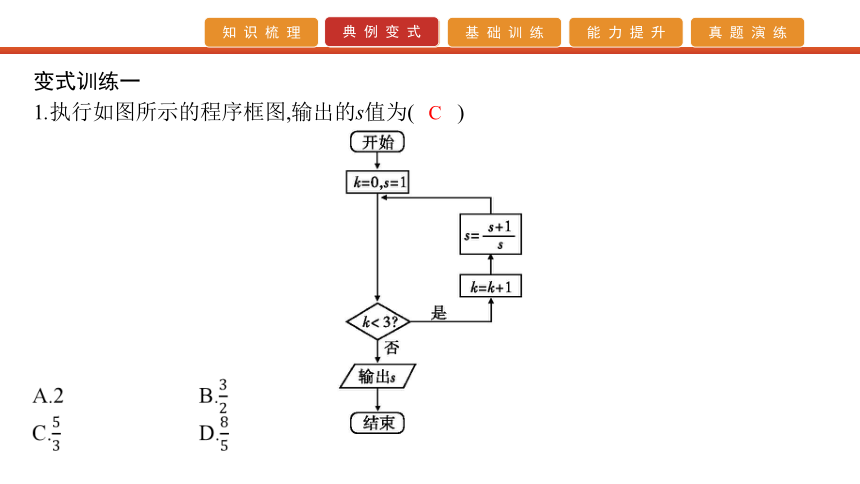
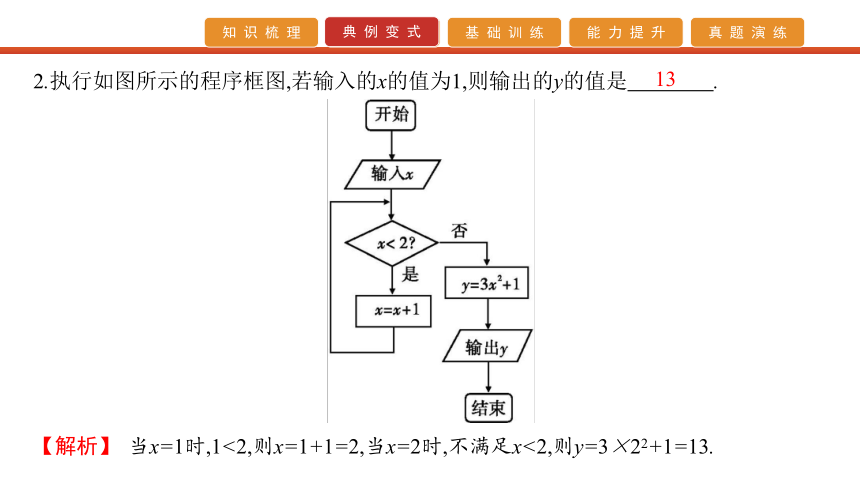
1.执行如图所示的程序框图,输出的s值为( )C 2.执行如图所示的程序框图,若输入的x的值为1,则输出的y的值是 .? 13 【解析】 当x=1时,1<2,则x=1+1=2,当x=2时,不满足x<2,则y=3×22+1=13. 3.如图所示的程序框图,该算法的功能是( )
A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值
B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值
C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值
D.计算[(1+2+3+…+(n-1)]2+(20+21+22+…+2n)的值C 【解析】 初始值k=1,S=0,第1次进入循环体时,S=1+20,k=2;
当第2次进入循环体时,S=1+20+2+21,k=3,…;
给定正整数n,当k=n时,最后一次进入循环体,
则有S=1+20+2+21+…+n+2n-1,k=n+1,终止循环体,输出S=(1+2+3+…+n)+(20+21+22+…+2n-1),故选C.题型二 框图中的数列问题
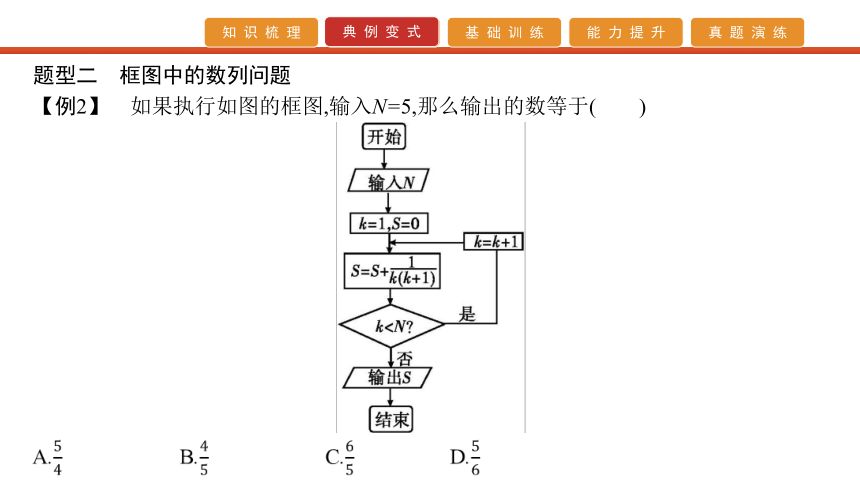
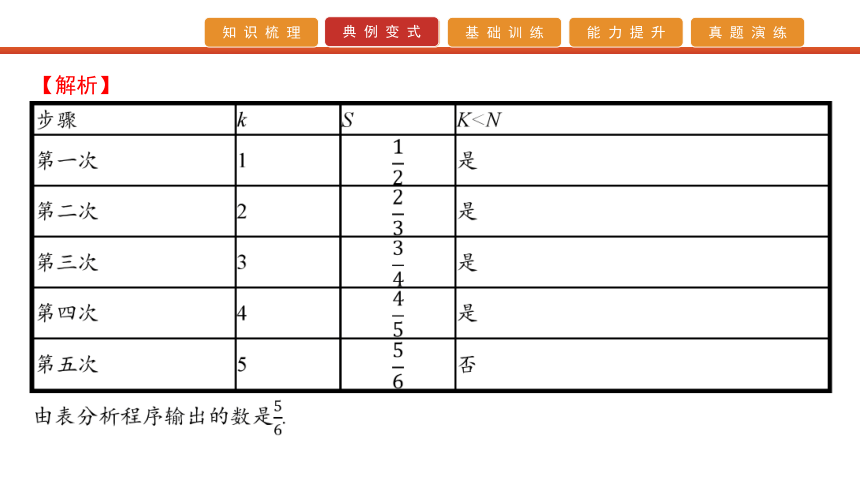
【例2】 如果执行如图的框图,输入N=5,那么输出的数等于( )【解析】 【答案】 D
【规律方法】解决算法问题应关注三点
(1)赋值号左边只能是变量(不能是表达式),在一个赋值语句中只能给一个变量赋值.
(2)注意条件结构与循环结构的联系:循环结构有重复性,条件结构具有选择性没有重复性.
(3)直到型循环是“先循环,后判断,条件满足时终止循环”,当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.变式训练二
1.已知向量a=(2,7),b=(x,-3),且a与b的夹角为钝角,则实数x的取值范围为( )D 2.阅读下边的程序框图,运行相应的程序,则输出S的值为( ) A.-10 B.6 C.14 D.18 B 【解析】 S=20,i=1,i=2i=2,S=S-i=20-2=18.
不满足i>S;
i=2i=4,S=S-i=18-4=14,不满足i>S;
i=2i=8,S=S-i=14-8=6,满足i>S,故输出S=6.题型三 程序框图的补全问题
【例3】 (2014·重庆卷)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )【答案】 C
【规律方法】
(1)循环结构中的条件判断
循环结构中的条件是高考的热点,主要是控制循环的变量应该满足的条件是什么.满足条件则进入循环或退出循环,此时要特别注意当型循环与直到型循环的区别.
(2)条件结构中的条件判断
条件结构中条件的判断关键是明确条件结构的功能,然后根据“是”的分支成立的条件进行判断.变式训练三
1.某程序框图如图所示,判断框内为“k≥n?”,n为正整数,若输出S=26,则判断框内的n= .?4 【解析】 依题意,第一次循环时,k=1+1=2,S=2×1+2=4;
第二次循环时,k=2+1=3,S=2×4+3=11;第三次循环时,k=3+1=4,S=2×11+4=26.因此当输出的S=26时,判断框内的n=4.2.某班有24名男生和26名女生,数据a1,a2,…,a50是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0),如图所示的程序用来同时统计全班成绩的平均数A,男生平均分M,女生平均分-W.为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其成绩的相反数,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )D 【解析】 依题意得,全班成绩的平均数应等于班级中所有的学生的成绩总和除以总人数,注意到当T>0时,输入的成绩表示的是某男生的成绩;当T<0时,输入的成绩表示的是某女生的成绩的相反数.因此结合题意得,选D.1.执行如图所示的程序框图,若输出的结果为3,则可输入的实数x值的个数为( )
A.1 B.2
C.3 D.4C 【解析】 当x>2时,由log2x=3得x=8;当x≤2时,由x2-1=3得x=2或x=-2.∴可输入的实数x值的个数为3.2.执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
A.0,0
B.1,1
C.0,1
D.1,0D 【解析】 第一次x=7,22<7,b=3,32>7,a=1;第二次x=9,22<9,b=3,32=9,a=0,故选D. 3.定义[x]为不超过x的最大整数,例如[1.3]=1.执行如图所示的程序框图,当输入的x为4.7时, 输出的y值为( )
A.7 B.8.6 C.10.2 D.11.8C【解析】 当输入的x为4.7时,由执行程序框图可知,4.7>3,4.7-[4.7]=0.7,即4.7-[4.7]不等于0,因而可得y=7+([4.7-3]+1)×1.6=10.2,即输出的y值为10.2.4.如图所示,程序框图的输出结果是( ) D 5.如图所示的程序框图,若输出结果为170,则判断框内应填入的条件为( )
A.i≥5? B.i≥7? C.i≥9? D.i≥11?C 【解析】 由模拟程序框图的运行过程,得该程序运行后是计算S=2+23+25+27=2+8+32+128=170,满足条件i=7+2≥9时,终止循环,
∴判断框中应填入的是i≥9.故选.C.6.执行如图所示的程序框图,若输入的a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
A.5 B.10 C.12 D.14D 【解析】 第一次循环:t=2×1-2=0,i=2;第二次循环:t=0+3=3,i=3;第三次循环:t=2×3-1 =5,i=4;第四次循环:t=2×5+4=14,i=5,不满足循环条件,退出循环,输出的t=14.7.(2018·惠州调研)执行如图所示的程序框图,则输出的结果为( )
A.7 B.9 C.10 D.11B 当i=9时, S=-lg(9+2)<-lg 10=-1,所以输出的i=9. 8.执行下图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5 B.4 C.3 D.2D 【解析】 阅读流程图,程序运行如下:
首先初始化数值:t=1,M=100,S=0,然后进入循环体:此时应满足t≤N,执行循环语句:t=t+1=3;此时不应满足S<91,可以跳出循环,则输入的正整数N的最小值为2. 中的(2)处应填的语句是( )
A.i>100,n=n+1 B.i>100,n=n+2
C.i>50,n=n+2 D.i≤50,n=n+2C =2(i-1),令2(i-1)=100,解得i=51,即需要i=51时输出.
故图中判断框内(1)处和执行框中的(2)处应填的语句分别是i>50,n=n+2.10.若x的取值范围为[0,10],给出如图所示的程序框图,输入一个数x,则输出的y<5的概
率为 .?若输出y=x+1(0≤x≤7),此时输出的结果应满足x+1<5,则0≤x<4,若输出y=x-1 (7A.k≥7 B.k>7
C.k≤8 D.k<8D 2.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
A.4 B.5 C.2 D.3A ( )
A.n≤2 016?
B.n≤2 017?
C.n>2 016?
D.n>2 017?B 分析可知判断框中可以填入的判断条件是“n≤2 017?”,选B. 4.(2019·武汉调研)执行如图所示的程序框图,若输入的x=2 017,则输出的i= .? 3 一、选择题 C C 3. (2018·全国卷Ⅱ)已知集合A={1,3,5,7}, B={2, 3,4,5},则A∩ B=( )
A.{3} B.{5}
C.{3,5} D.{1,2,3,4,5,7}4.(2018·北京卷)在复平面内,复数 的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限C 【解析】 ∵A={1,3,5,7},B={2,3,4,5},∴A∩B={3,5},故选C. D 故选D. 5. (2018·北京卷)执行如图所示的程序框图,输出的s值为( ) B 【解析】 初始化数值k=1,s=1,
循环结果执行如下:故选B. 6.(2017·全国卷Ⅱ) 设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A.{1,-3} B.{1,0}
C.{1,3} D.{1,5}C 【解析】 因为A∩B={1},所以方程x2-4x+m=0有一个根为1,得m=3,
此时方程为x2-4x+3=0,∴该方程的另一个根为3,故B={1,3}.C ?8.(2017·山东卷)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
A.p∧q B.p∧ q
C. p∧q D. p∧ qB 【解析】 因为x>0时,x+1>1,所以ln(x+1)>0,所以p为真命题.若a>b,可取a=1,b=-2,此时a21000的最小偶数n,那么在 和?两个空白框中,可以分别填入( )
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2D 【解析】 判断框“ ”中应填入A≤1000,由于是求最小偶数,故处理框“ ”中应填入n=n+2.选D.11.(2019·全国卷Ⅱ)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )
A.(-1,+∞)
B.(-∞,2)
C.(-1,2)
D.?C 【解析】 由题知A∩B=(-1,2),故选C. 12.(2019·全国卷Ⅱ)设z=i(2+i),则 =( )
A.1+2i B.-1+2i
C.1-2i D.-1-2iD 【解析】 z=i(2+i)=2i+i2=-1+2i,所以 =-1-2i,选D. 二、填空题
13.(2019·全国卷Ⅱ)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.
甲:我的成绩比乙高.
乙:丙的成绩比我和甲的都高.
丙:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为( )
A.甲、乙、丙 B.乙、甲、丙
C.丙、乙、甲 D.甲、丙、乙A【解析】 若甲预测正确,则乙、丙预测错误,则甲比乙成绩高,丙比乙成绩低,故3人成绩由高到低依次为甲,乙,丙;若乙预测正确,则丙预测也正确,不符合题意;若丙预测正确,则甲必预测错误,丙比乙的成绩高,乙比甲成绩高,即丙比甲,乙成绩都高,即乙预测正确,不符合题意,故选A.15.(2019·全国卷Ⅲ)若z(1+i)=2i,则z=( )
A.-1-i B.-1+i
C.1-i D.1+i?A D 16.(2019·全国卷Ⅲ)执行如图所示的程序框图,如果输入的ε为0.01,则输出s的值等于( )C 【解析】 输入的ε为0.01,
x=1,S=0+1,x=0.5不满足条件退出循环的条件x<0.01;
(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.
(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.
2.程序框图
程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.
3.三种基本逻辑结构 题型一 程序框图的执行问题
【例1】 (2016·全国卷Ⅰ)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.y=2x B.y=3x C.y=4x D.y=5x
【解析】 输入x=0,y=1,n=1,
运行第一次,x=0,y=1,不满足x2+y2≥36;【答案】 C【规律方法】利用循环结构表示算法的步骤
第一要先确定是利用当型循环结构,还是利用直到型循环结构;
第二要选择准确的表示累计的变量;
第三要注意在哪一步开始循环,满足什么条件不再执行循环体.变式训练一
1.执行如图所示的程序框图,输出的s值为( )C 2.执行如图所示的程序框图,若输入的x的值为1,则输出的y的值是 .? 13 【解析】 当x=1时,1<2,则x=1+1=2,当x=2时,不满足x<2,则y=3×22+1=13. 3.如图所示的程序框图,该算法的功能是( )
A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值
B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值
C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值
D.计算[(1+2+3+…+(n-1)]2+(20+21+22+…+2n)的值C 【解析】 初始值k=1,S=0,第1次进入循环体时,S=1+20,k=2;
当第2次进入循环体时,S=1+20+2+21,k=3,…;
给定正整数n,当k=n时,最后一次进入循环体,
则有S=1+20+2+21+…+n+2n-1,k=n+1,终止循环体,输出S=(1+2+3+…+n)+(20+21+22+…+2n-1),故选C.题型二 框图中的数列问题
【例2】 如果执行如图的框图,输入N=5,那么输出的数等于( )【解析】 【答案】 D
【规律方法】解决算法问题应关注三点
(1)赋值号左边只能是变量(不能是表达式),在一个赋值语句中只能给一个变量赋值.
(2)注意条件结构与循环结构的联系:循环结构有重复性,条件结构具有选择性没有重复性.
(3)直到型循环是“先循环,后判断,条件满足时终止循环”,当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.变式训练二
1.已知向量a=(2,7),b=(x,-3),且a与b的夹角为钝角,则实数x的取值范围为( )D 2.阅读下边的程序框图,运行相应的程序,则输出S的值为( ) A.-10 B.6 C.14 D.18 B 【解析】 S=20,i=1,i=2i=2,S=S-i=20-2=18.
不满足i>S;
i=2i=4,S=S-i=18-4=14,不满足i>S;
i=2i=8,S=S-i=14-8=6,满足i>S,故输出S=6.题型三 程序框图的补全问题
【例3】 (2014·重庆卷)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )【答案】 C
【规律方法】
(1)循环结构中的条件判断
循环结构中的条件是高考的热点,主要是控制循环的变量应该满足的条件是什么.满足条件则进入循环或退出循环,此时要特别注意当型循环与直到型循环的区别.
(2)条件结构中的条件判断
条件结构中条件的判断关键是明确条件结构的功能,然后根据“是”的分支成立的条件进行判断.变式训练三
1.某程序框图如图所示,判断框内为“k≥n?”,n为正整数,若输出S=26,则判断框内的n= .?4 【解析】 依题意,第一次循环时,k=1+1=2,S=2×1+2=4;
第二次循环时,k=2+1=3,S=2×4+3=11;第三次循环时,k=3+1=4,S=2×11+4=26.因此当输出的S=26时,判断框内的n=4.2.某班有24名男生和26名女生,数据a1,a2,…,a50是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0),如图所示的程序用来同时统计全班成绩的平均数A,男生平均分M,女生平均分-W.为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其成绩的相反数,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )D 【解析】 依题意得,全班成绩的平均数应等于班级中所有的学生的成绩总和除以总人数,注意到当T>0时,输入的成绩表示的是某男生的成绩;当T<0时,输入的成绩表示的是某女生的成绩的相反数.因此结合题意得,选D.1.执行如图所示的程序框图,若输出的结果为3,则可输入的实数x值的个数为( )
A.1 B.2
C.3 D.4C 【解析】 当x>2时,由log2x=3得x=8;当x≤2时,由x2-1=3得x=2或x=-2.∴可输入的实数x值的个数为3.2.执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
A.0,0
B.1,1
C.0,1
D.1,0D 【解析】 第一次x=7,22<7,b=3,32>7,a=1;第二次x=9,22<9,b=3,32=9,a=0,故选D. 3.定义[x]为不超过x的最大整数,例如[1.3]=1.执行如图所示的程序框图,当输入的x为4.7时, 输出的y值为( )
A.7 B.8.6 C.10.2 D.11.8C【解析】 当输入的x为4.7时,由执行程序框图可知,4.7>3,4.7-[4.7]=0.7,即4.7-[4.7]不等于0,因而可得y=7+([4.7-3]+1)×1.6=10.2,即输出的y值为10.2.4.如图所示,程序框图的输出结果是( ) D 5.如图所示的程序框图,若输出结果为170,则判断框内应填入的条件为( )
A.i≥5? B.i≥7? C.i≥9? D.i≥11?C 【解析】 由模拟程序框图的运行过程,得该程序运行后是计算S=2+23+25+27=2+8+32+128=170,满足条件i=7+2≥9时,终止循环,
∴判断框中应填入的是i≥9.故选.C.6.执行如图所示的程序框图,若输入的a0=4,a1=-1,a2=3,a3=-2,a4=1,则输出的t的值为( )
A.5 B.10 C.12 D.14D 【解析】 第一次循环:t=2×1-2=0,i=2;第二次循环:t=0+3=3,i=3;第三次循环:t=2×3-1 =5,i=4;第四次循环:t=2×5+4=14,i=5,不满足循环条件,退出循环,输出的t=14.7.(2018·惠州调研)执行如图所示的程序框图,则输出的结果为( )
A.7 B.9 C.10 D.11B 当i=9时, S=-lg(9+2)<-lg 10=-1,所以输出的i=9. 8.执行下图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5 B.4 C.3 D.2D 【解析】 阅读流程图,程序运行如下:
首先初始化数值:t=1,M=100,S=0,然后进入循环体:此时应满足t≤N,执行循环语句:t=t+1=3;此时不应满足S<91,可以跳出循环,则输入的正整数N的最小值为2. 中的(2)处应填的语句是( )
A.i>100,n=n+1 B.i>100,n=n+2
C.i>50,n=n+2 D.i≤50,n=n+2C =2(i-1),令2(i-1)=100,解得i=51,即需要i=51时输出.
故图中判断框内(1)处和执行框中的(2)处应填的语句分别是i>50,n=n+2.10.若x的取值范围为[0,10],给出如图所示的程序框图,输入一个数x,则输出的y<5的概
率为 .?若输出y=x+1(0≤x≤7),此时输出的结果应满足x+1<5,则0≤x<4,若输出y=x-1 (7
C.k≤8 D.k<8D 2.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
A.4 B.5 C.2 D.3A ( )
A.n≤2 016?
B.n≤2 017?
C.n>2 016?
D.n>2 017?B 分析可知判断框中可以填入的判断条件是“n≤2 017?”,选B. 4.(2019·武汉调研)执行如图所示的程序框图,若输入的x=2 017,则输出的i= .? 3 一、选择题 C C 3. (2018·全国卷Ⅱ)已知集合A={1,3,5,7}, B={2, 3,4,5},则A∩ B=( )
A.{3} B.{5}
C.{3,5} D.{1,2,3,4,5,7}4.(2018·北京卷)在复平面内,复数 的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限C 【解析】 ∵A={1,3,5,7},B={2,3,4,5},∴A∩B={3,5},故选C. D 故选D. 5. (2018·北京卷)执行如图所示的程序框图,输出的s值为( ) B 【解析】 初始化数值k=1,s=1,
循环结果执行如下:故选B. 6.(2017·全国卷Ⅱ) 设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A.{1,-3} B.{1,0}
C.{1,3} D.{1,5}C 【解析】 因为A∩B={1},所以方程x2-4x+m=0有一个根为1,得m=3,
此时方程为x2-4x+3=0,∴该方程的另一个根为3,故B={1,3}.C ?8.(2017·山东卷)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
A.p∧q B.p∧ q
C. p∧q D. p∧ qB 【解析】 因为x>0时,x+1>1,所以ln(x+1)>0,所以p为真命题.若a>b,可取a=1,b=-2,此时a2
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2D 【解析】 判断框“ ”中应填入A≤1000,由于是求最小偶数,故处理框“ ”中应填入n=n+2.选D.11.(2019·全国卷Ⅱ)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )
A.(-1,+∞)
B.(-∞,2)
C.(-1,2)
D.?C 【解析】 由题知A∩B=(-1,2),故选C. 12.(2019·全国卷Ⅱ)设z=i(2+i),则 =( )
A.1+2i B.-1+2i
C.1-2i D.-1-2iD 【解析】 z=i(2+i)=2i+i2=-1+2i,所以 =-1-2i,选D. 二、填空题
13.(2019·全国卷Ⅱ)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.
甲:我的成绩比乙高.
乙:丙的成绩比我和甲的都高.
丙:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为( )
A.甲、乙、丙 B.乙、甲、丙
C.丙、乙、甲 D.甲、丙、乙A【解析】 若甲预测正确,则乙、丙预测错误,则甲比乙成绩高,丙比乙成绩低,故3人成绩由高到低依次为甲,乙,丙;若乙预测正确,则丙预测也正确,不符合题意;若丙预测正确,则甲必预测错误,丙比乙的成绩高,乙比甲成绩高,即丙比甲,乙成绩都高,即乙预测正确,不符合题意,故选A.15.(2019·全国卷Ⅲ)若z(1+i)=2i,则z=( )
A.-1-i B.-1+i
C.1-i D.1+i?A D 16.(2019·全国卷Ⅲ)执行如图所示的程序框图,如果输入的ε为0.01,则输出s的值等于( )C 【解析】 输入的ε为0.01,
x=1,S=0+1,x=0.5不满足条件退出循环的条件x<0.01;
同课章节目录
