2020版高考艺考生文化课百日冲刺 第2讲 复数、推理与证明(课件:37张PPT)
文档属性
| 名称 | 2020版高考艺考生文化课百日冲刺 第2讲 复数、推理与证明(课件:37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-02 00:00:00 | ||
图片预览











文档简介
课件37张PPT。第2讲 复数、推理与证明1.复数的有关概念
(1)复数的定义:形如a+bi(a,b∈R)的数叫做复数,其中实部是a,虚部是b.
(2)复数的分类:(3)复数相等:a+bi=c+di?a=c且b=d(a,b,c,d∈R).
(4)共轭复数:a+bi与c+di共轭?a=c且b=-d(a,b,c,d∈R).2.复数的运算法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),则:
(1)z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;
(2)z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;
(3)z1·z2=(a+bi)(c+di)=(ac-bd)+(ad+bc)i;3.复数的几何意义
(1)复平面的概念:建立直角坐标系来表示复数的平面叫做复平面.
(2)实轴、虚轴:在复平面内,x轴叫做实轴,y轴叫做虚轴,实轴上的点都表示实数;除原点以外,虚轴上的点都表示纯虚数.4.合情推理 5.演绎推理
(1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.
(2)模式:“三段论”是演绎推理的一般模式,包括:
①大前提——已知的一般原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.(3)特点:演绎推理是由一般到特殊的推理,直接证明 6.反证法
假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.
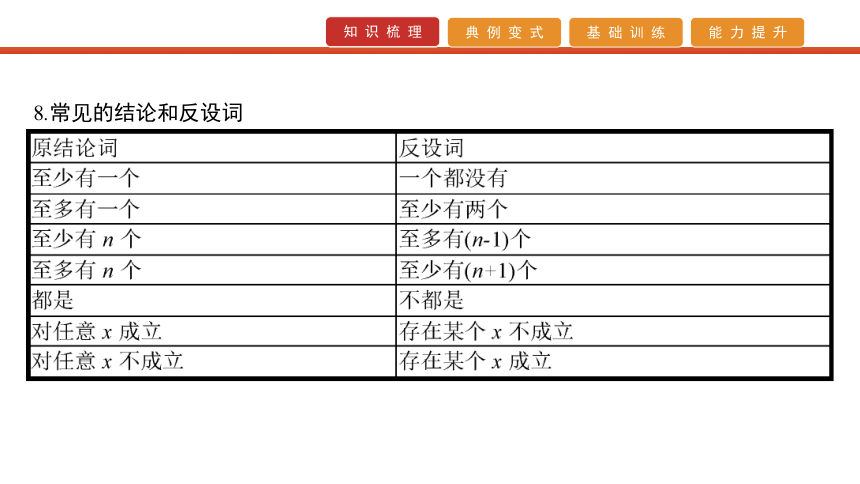
7.用反证法证明问题的一般步骤8.常见的结论和反设词 A.-3 B.-1 C.1 D.3 ∴a-3=0,∴a=3.
(2)由已知得3+bi=(1-i)(a+bi)=a+bi-ai-bi2=(a+b)+(b-a)i,根据复数相等的条件,【答案】 (1)D (2)3 【规律方法】解决复数概念问题的方法及注意事项
(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.
(2)解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.变式训练一
1.设m∈R,复数z=m2-1+(m+1)i表示纯虚数,则m的值为( )
A.1 B.-1
C.±1 D.02.(2016·全国卷Ⅰ)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( ) ABA.i B.-i
C.2i D.-2i4.(2016·全国卷Ⅰ)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )
A.-3 B.-2
C.2 D.3A A 【解析】 (1+2i)(a+i)=a-2+(1+2a)i,由题意知a-2=1+2a,解得a=-3,故选A. 题型二 复数的运算 (2)(2018·江苏卷)若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为 .?
(3)若复数z满足2z+ =3-2i,其中i为虚数单位,则z等于( )
A.1+2i B.1-2i
C.-1+2i D.-1-2i故z的实部为2.
(3)设z=a+bi(a,b∈R),则 =a-bi,所以2(a+bi)+(a-bi)=3-2i,整理得3a+bi=3-2i,所以z=1-2i,故选B.
【答案】(1)4-i (2)2 (3)B【规律方法】复数代数形式运算问题的常见类型及解题策略
(1)复数的乘法.复数的乘法类似于多项式的四则运算,可将含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可.
(2)复数的除法.除法的关键是分子分母同乘以分母的共轭复数,解题时要注意把i的幂写成最简形式.
(3)复数的运算与复数概念的综合题.先利用复数的运算法则化简,一般化为a+bi(a,b∈R)的形式,再结合相关定义解答.
(4)复数的运算与复数几何意义的综合题.先利用复数的运算法则化简,一般化为a+bi(a,b∈R)的形式,再结合复数的几何意义解答.
(5)复数的综合运算.分别运用复数的乘法、除法法则进行运算,要注意运算顺序,要先算乘除,后算加减,有括号要先算括号里面的. 变式训练二 2.(2019·惠州模拟)已知复数z的共轭复数为 ,若 (1-i)=2i(i为虚数单位),则z=( )
A.i B.i-1
C.-i-1 D.-iA C D【解析】 对四个选项逐一验证可知,当z=1-i时,符合题意,故选D. 题型三 复数的几何意义
【例3】 (1)(2019·郑州模拟)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(-∞,1) B.(-∞,-1)
C.(1,+∞) D.(-1,+∞)A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】 (1)复数(1-i)(a+i)=a+1+(1-a)i,其在复平面内对应的点(a+1,1-a)在第二象限, 【答案】 (1)B (2)B
【规律方法】复数的几何意义及应用
(1)复数z、复平面上的点Z及向量 相互联系,即z=a+bi(a,b∈R)?Z(a,b)? .
(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.变式训练三
1.(2019·广州模拟)设z=1+i(i是虚数单位),则复数 +z2在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限( )
A.1+2i B.1-2i C.-2+i D.2+iA 所以该复数在复平面内对应的点的坐标为(1,1),位于第一象限,故选A. C 其对应的点的坐标是(2,1),因此点A(-2,1),其对应的复数为-2+i,故选C. 题型四 合情推理、演绎推理
【例4】 (1)给出以下数对序列:
(1,1);
(1,2)(2,1);
(1,3)(2,2)(3,1);
(1,4)(2,3)(3,2)(4,1);
……
记第i行的第j个数对为aij,如a43=(3,2),则anm=( )
A.(m,n-m+1) B.(m-1,n-m)
C.(m-1,n-m+1) D.(m,n-m)【解析】 (1)由已知可得,第i行第j列个数对aij=(j,i-j+1),因此anm=(m,n-m+1),故选A.
(2)第一个式子是n=1的情况,此时a=11=1;第二个式子是n=2的情况,此时a=22=4;第三个式子是n=3的情况,此时a=33=27,归纳可知a=nn.
【答案】(1)A (2)nn
【规律方法】推理问题的常见类型及解题策略
(1)与“数字”相关问题:主要是观察数字特点,找出等式左右两侧的规律.
(2)与不等式有关的推理:观察所给几个不等式两边式子的特点,注意纵向看、找出隐含规律.
(3)与图形有关推理:合理利用特殊图形归纳推理得出结论. 变式训练四
1.有一个奇数组成的数阵排列如下:
1 3 7 13 21 …
5 9 15 23 … …
11 17 25 … … …
19 27 … … … …
29 … … … … …
… … … … … …
则第30行从左到右第3个数是 .?1 051 【解析】 观察每一行的第一个数,由归纳推理可得第30行的第1个数是1+4+6+8+10+…+60= -1=929.又第n行从左到右的第2个数比第1个数大2n,第3个数比第2个数大2n+2,所以第30行从左到右的第2个数比第1个数大60,第3个数比第2个数大62,故第30行从左到右第3个数是929+60+62=1 051.2.(2017·全国卷Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩
B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩D【解析】 由题意可知,甲看乙丙的成绩,因此乙和丙一个是优秀,一个是良好,所以丁知道甲的成绩后,就能够知道自己的成绩,但是丁不知道乙和丙的成绩.综上所述,乙丁可以知道自己的成绩.3.观察下图,可推断出“x”处应该填的数字是 .? 183 【解析】 由前两个图形发现:中间数等于四周四个数的平方和,所以“x”处应填的数字是32+52+72+102=183.A.i B.2-i
C.1-i D.0D B 点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限A.i B.1 C.-i D.-1 B 所以x+yi=-2+3i,其在复平面内对应的点为(-2,3),位于第二象限,故选B. C 5.将正整数排列如下图:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
…
则图中数2 018出现在( )
A.第44行第83列 B.第45行第83列
C.第44行第82列 D.第45行第82列D 【解析】 由题意可知第n行有2n-1个数,则前n行的数的个数为1+3+5+…+(2n-1)=n2,因为442=1 936,452=2 025,且1 936<2 018<2 025,所以2 018在第45行,又2 018-1 936=82,故2 018在第45行第82列.A.-3 B.-2
C.-1 D.1A A 【解析】 根据分面包原理知,等式右边第一个数的分母应是等式左边数的分母加1的一半,第二个数的分母是第一个数的分母与等式左边数的分母的乘积,两个数的原始分1.设z1,z2是复数,则下列命题中的假命题是( ) D 2.如图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N)个点,相C【解析】 每条边有n个点,所以三条边有3n个点,三角形的3个顶点都被重复计算了一次,4.(2019·邢台模拟)复数z1=2+i,若复数z1,z2在复平面内的对应点关于虚轴对称,则z1z2=( )
A.-5 B.5
C.-3+4i D.3-4iAA【解析】 由题意,得z2=-2+i,则z1z2=(2+i)(-2+i)=i2-4=-5,故选A.
(1)复数的定义:形如a+bi(a,b∈R)的数叫做复数,其中实部是a,虚部是b.
(2)复数的分类:(3)复数相等:a+bi=c+di?a=c且b=d(a,b,c,d∈R).
(4)共轭复数:a+bi与c+di共轭?a=c且b=-d(a,b,c,d∈R).2.复数的运算法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),则:
(1)z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;
(2)z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;
(3)z1·z2=(a+bi)(c+di)=(ac-bd)+(ad+bc)i;3.复数的几何意义
(1)复平面的概念:建立直角坐标系来表示复数的平面叫做复平面.
(2)实轴、虚轴:在复平面内,x轴叫做实轴,y轴叫做虚轴,实轴上的点都表示实数;除原点以外,虚轴上的点都表示纯虚数.4.合情推理 5.演绎推理
(1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.
(2)模式:“三段论”是演绎推理的一般模式,包括:
①大前提——已知的一般原理;
②小前提——所研究的特殊情况;
③结论——根据一般原理,对特殊情况做出的判断.(3)特点:演绎推理是由一般到特殊的推理,直接证明 6.反证法
假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法.
7.用反证法证明问题的一般步骤8.常见的结论和反设词 A.-3 B.-1 C.1 D.3 ∴a-3=0,∴a=3.
(2)由已知得3+bi=(1-i)(a+bi)=a+bi-ai-bi2=(a+b)+(b-a)i,根据复数相等的条件,【答案】 (1)D (2)3 【规律方法】解决复数概念问题的方法及注意事项
(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.
(2)解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.变式训练一
1.设m∈R,复数z=m2-1+(m+1)i表示纯虚数,则m的值为( )
A.1 B.-1
C.±1 D.02.(2016·全国卷Ⅰ)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( ) ABA.i B.-i
C.2i D.-2i4.(2016·全国卷Ⅰ)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )
A.-3 B.-2
C.2 D.3A A 【解析】 (1+2i)(a+i)=a-2+(1+2a)i,由题意知a-2=1+2a,解得a=-3,故选A. 题型二 复数的运算 (2)(2018·江苏卷)若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为 .?
(3)若复数z满足2z+ =3-2i,其中i为虚数单位,则z等于( )
A.1+2i B.1-2i
C.-1+2i D.-1-2i故z的实部为2.
(3)设z=a+bi(a,b∈R),则 =a-bi,所以2(a+bi)+(a-bi)=3-2i,整理得3a+bi=3-2i,所以z=1-2i,故选B.
【答案】(1)4-i (2)2 (3)B【规律方法】复数代数形式运算问题的常见类型及解题策略
(1)复数的乘法.复数的乘法类似于多项式的四则运算,可将含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可.
(2)复数的除法.除法的关键是分子分母同乘以分母的共轭复数,解题时要注意把i的幂写成最简形式.
(3)复数的运算与复数概念的综合题.先利用复数的运算法则化简,一般化为a+bi(a,b∈R)的形式,再结合相关定义解答.
(4)复数的运算与复数几何意义的综合题.先利用复数的运算法则化简,一般化为a+bi(a,b∈R)的形式,再结合复数的几何意义解答.
(5)复数的综合运算.分别运用复数的乘法、除法法则进行运算,要注意运算顺序,要先算乘除,后算加减,有括号要先算括号里面的. 变式训练二 2.(2019·惠州模拟)已知复数z的共轭复数为 ,若 (1-i)=2i(i为虚数单位),则z=( )
A.i B.i-1
C.-i-1 D.-iA C D【解析】 对四个选项逐一验证可知,当z=1-i时,符合题意,故选D. 题型三 复数的几何意义
【例3】 (1)(2019·郑州模拟)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(-∞,1) B.(-∞,-1)
C.(1,+∞) D.(-1,+∞)A.第一象限 B.第二象限
C.第三象限 D.第四象限【解析】 (1)复数(1-i)(a+i)=a+1+(1-a)i,其在复平面内对应的点(a+1,1-a)在第二象限, 【答案】 (1)B (2)B
【规律方法】复数的几何意义及应用
(1)复数z、复平面上的点Z及向量 相互联系,即z=a+bi(a,b∈R)?Z(a,b)? .
(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.变式训练三
1.(2019·广州模拟)设z=1+i(i是虚数单位),则复数 +z2在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限( )
A.1+2i B.1-2i C.-2+i D.2+iA 所以该复数在复平面内对应的点的坐标为(1,1),位于第一象限,故选A. C 其对应的点的坐标是(2,1),因此点A(-2,1),其对应的复数为-2+i,故选C. 题型四 合情推理、演绎推理
【例4】 (1)给出以下数对序列:
(1,1);
(1,2)(2,1);
(1,3)(2,2)(3,1);
(1,4)(2,3)(3,2)(4,1);
……
记第i行的第j个数对为aij,如a43=(3,2),则anm=( )
A.(m,n-m+1) B.(m-1,n-m)
C.(m-1,n-m+1) D.(m,n-m)【解析】 (1)由已知可得,第i行第j列个数对aij=(j,i-j+1),因此anm=(m,n-m+1),故选A.
(2)第一个式子是n=1的情况,此时a=11=1;第二个式子是n=2的情况,此时a=22=4;第三个式子是n=3的情况,此时a=33=27,归纳可知a=nn.
【答案】(1)A (2)nn
【规律方法】推理问题的常见类型及解题策略
(1)与“数字”相关问题:主要是观察数字特点,找出等式左右两侧的规律.
(2)与不等式有关的推理:观察所给几个不等式两边式子的特点,注意纵向看、找出隐含规律.
(3)与图形有关推理:合理利用特殊图形归纳推理得出结论. 变式训练四
1.有一个奇数组成的数阵排列如下:
1 3 7 13 21 …
5 9 15 23 … …
11 17 25 … … …
19 27 … … … …
29 … … … … …
… … … … … …
则第30行从左到右第3个数是 .?1 051 【解析】 观察每一行的第一个数,由归纳推理可得第30行的第1个数是1+4+6+8+10+…+60= -1=929.又第n行从左到右的第2个数比第1个数大2n,第3个数比第2个数大2n+2,所以第30行从左到右的第2个数比第1个数大60,第3个数比第2个数大62,故第30行从左到右第3个数是929+60+62=1 051.2.(2017·全国卷Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
A.乙可以知道四人的成绩
B.丁可以知道四人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩D【解析】 由题意可知,甲看乙丙的成绩,因此乙和丙一个是优秀,一个是良好,所以丁知道甲的成绩后,就能够知道自己的成绩,但是丁不知道乙和丙的成绩.综上所述,乙丁可以知道自己的成绩.3.观察下图,可推断出“x”处应该填的数字是 .? 183 【解析】 由前两个图形发现:中间数等于四周四个数的平方和,所以“x”处应填的数字是32+52+72+102=183.A.i B.2-i
C.1-i D.0D B 点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限A.i B.1 C.-i D.-1 B 所以x+yi=-2+3i,其在复平面内对应的点为(-2,3),位于第二象限,故选B. C 5.将正整数排列如下图:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
…
则图中数2 018出现在( )
A.第44行第83列 B.第45行第83列
C.第44行第82列 D.第45行第82列D 【解析】 由题意可知第n行有2n-1个数,则前n行的数的个数为1+3+5+…+(2n-1)=n2,因为442=1 936,452=2 025,且1 936<2 018<2 025,所以2 018在第45行,又2 018-1 936=82,故2 018在第45行第82列.A.-3 B.-2
C.-1 D.1A A 【解析】 根据分面包原理知,等式右边第一个数的分母应是等式左边数的分母加1的一半,第二个数的分母是第一个数的分母与等式左边数的分母的乘积,两个数的原始分1.设z1,z2是复数,则下列命题中的假命题是( ) D 2.如图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N)个点,相C【解析】 每条边有n个点,所以三条边有3n个点,三角形的3个顶点都被重复计算了一次,4.(2019·邢台模拟)复数z1=2+i,若复数z1,z2在复平面内的对应点关于虚轴对称,则z1z2=( )
A.-5 B.5
C.-3+4i D.3-4iAA【解析】 由题意,得z2=-2+i,则z1z2=(2+i)(-2+i)=i2-4=-5,故选A.
同课章节目录
